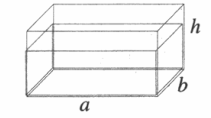
Чем измеряется глубина бочки физика

Гидростатическое давление: формула и свойства.

Гидростатическое давление – это давление, производимое на жидкость силой тяжести.

Гидростатикой называется раздел гидравлики, в котором изучаются законы равновесия жидкостей и рассматривается практическое приложение этих законов.

Для того, чтобы понять гидростатику необходимо определиться в некоторых понятиях и определениях.

В этой статье мы подготовили для Вас, всю необходимую информацию о гидростатическом давлении, начиная от закона Паскаля и определения формулы гидростатического давления и до свойств давления и применения законов гидростатики в повседневной жизни.

Содержание статьи

Закон Паскаля для гидростатики.

В 1653 году французским ученым Б. Паскалем был открыт закон, который принято называть основным законом гидростатики.

Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.

Закон Паскаля легко понимается если взглянуть на молекулярное строение вещества. В жидкостях и газах молекулы обладают относительной свободой, они способны перемещаться друг относительно друга, в отличии от твердых тел. В твердых телах молекулы собраны в кристаллические решетки.

Относительная свобода, которой обладают молекулы жидкостей и газов, позволяет передавать давление производимое на жидкость или газ не только в направлении действия силы, но и во всех других направлениях.

Закон Паскаля для гидростатики нашел широкое распространение в промышленности. На этом законе основана работа гидроавтоматики, управляющей станками с ЧПУ, автомобилями и самолетами и многих других гидравлических машин.

Определение и формула гидростатического давления

Из описанного выше закона Паскаля вытекает, что:

Величина гидростатического давления не зависит от формы сосуда, в котором находится жидкость и определяется произведением

ρ – плотность жидкости

g – ускорение свободного падения

h – глубина, на которой определяется давление.

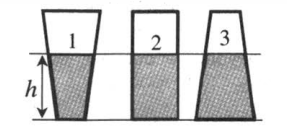
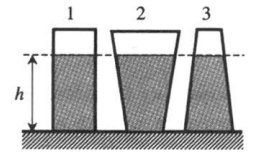
Для иллюстрации этой формулы посмотрим на 3 сосуда разной формы.

Во всех трёх случаях давление жидкости на дно сосуда одинаково.

Полное давление жидкости в сосуде равно

P0 – давление на поверхности жидкости. В большинстве случаев принимается равным атмосферному.

Сила гидростатического давления

Выделим в жидкости, находящейся в равновесии, некоторый объем, затем рассечем его произвольной плоскостью АВ на две части и мысленно отбросим одну из этих частей, например верхнюю. При этом мы должны приложить к плоскости АВ силы, действие которых будет эквивалентно действию отброшенной верхней части объема на оставшуюся нижнюю его часть.

Рассмотрим в плоскости сечения АВ замкнутый контур площадью ΔF, включающий в себя некоторую произвольную точку a. Пусть на эту площадь воздействует сила ΔP.

Тогда гидростатическое давление формула которого выглядит как

представляет собой силу, действующую на единицу площади, будет называться средним гидростатическим давлением или средним напряжением гидростатического давления по площади ΔF.

Истинное давление в разных точках этой площади может быть разным: в одних точках оно может быть больше, в других – меньше среднего гидростатического давления. Очевидно, что в общем случае среднее давление Рср будет тем меньше отличаться от истинного давления в точке а, чем меньше будет площадь ΔF, и в пределе среднее давление совпадет с истинным давлением в точке а.

Для жидкостей, находящихся в равновесии, гидростатическое давление жидкости аналогично напряжению сжатия в твердых телах.

Единицей измерения давления в системе СИ является ньютон на квадратный метр (Н/м 2 ) – её называют паскалем (Па). Поскольку величина паскаля очень мала, часто применяют укрупненные единицы:

килоньютон на квадратный метр – 1кН/м 2 = 1*10 3 Н/м 2

меганьютон на квадратный метр – 1МН/м 2 = 1*10 6 Н/м 2

Давление равное 1*10 5 Н/м 2 называется баром (бар).

Между всеми этими единицами существует следующее соотношение:

1ат = 1 кгс/см 2 = 0,98 бар = 0,98 * 10 5 Па = 0,98 * 10 6 дин = 10 4 кгс/м 2

Следует помнить что между технической атмосферой (ат) и атмосферой физической (Ат) существует разница. 1 Ат = 1,033 кгс/см 2 и представляет собой нормальное давление на уровне моря. Атмосферное давление зависит от высоты расположения места над уровнем моря.

Измерение гидростатического давления

На практике применяют различные способы учета величины гидростатического давления. Если при определении гидростатического давления принимается во внимание и атмосферное давление, действующее на свободную поверхность жидкости, его называют полным или абсолютным. В этом случае величина давления обычно измеряется в технических атмосферах, называемых абсолютными (ата).

Часто при учете давления атмосферное давление на свободной поверхности не принимают во внимание, определяя так называемое избыточное гидростатическое давление, или манометрическое давление, т.е. давление сверх атмосферного.

Манометрическое давление определяют как разность между абсолютным давлением в жидкости и давлением атмосферным.

и измеряют также в технических атмосферах, называемых в этом случае избыточными.

Случается, что гидростатическое давление в жидкости оказывается меньше атмосферного. В этом случае говорят, что в жидкости имеется вакуум. Величина вакуума равняется разнице между атмосферным и и абсолютным давлением в жидкости

и измеряется в пределах от нуля до атмосферы.

Свойства гидростатического давления

Гидростатическое давление воды обладает двумя основными свойствами:
Оно направлено по внутренней нормали к площади, на которую действует;
Величина давления в данной точке не зависит от направления (т.е. от ориентированности в пространстве площадки, на которой находится точка).

Первое свойство является простым следствием того положения, что в покоящейся жидкости отсутствуют касательные и растягивающие усилия.

Предположим, что гидростатическое давление направлено не по нормали, т.е. не перпендикулярно, а под некоторым углом к площадке. Тогда его можно разложить на две составляющие – нормальную и касательную. Наличие касательной составляющей из-за отсутствия в покоящейся жидкости сил сопротивления сдвигающим усилиям неизбежно привело бы к движению жидкости вдоль площадки, т.е. нарушило бы её равновесие.

Поэтому единственным возможным направлением гидростатического давления является его направление по нормали к площадке.

Если предположить что гидростатическое давление направлено не по внутренней, а по внешней нормали, т.е. не внутрь рассматриваемого объекта а наружу от него, то вследствие того, что жидкость не оказывает сопротивления растягивающим усилиям – частицы жидкости пришли бы в движение и её равновесие было бы нарушено.

Следовательно, гидростатическое давление воды всегда направлено по внутренней нормали и представляет собой сжимающее давление.

Из этого же правило следует, что если измениться давление в какой-то точке, то на такую же величину измениться давление в любой другой точке этой жидкости. В этом заключается закон Паскаля, который формулируется следующим образом: Давление производимое на жидкость, передается внутри жидкости во все стороны с одинаковой силой.

На применение этого закона основываются действие машин, работающих под гидростатическим давлением.

Ещё одним фактором влияющим на величину давления является вязкость жидкости, которой до недавнего времени приято было пренебрегать. С появлением агрегатов работающих на высоком давлении вязкость пришлось так же учитывать. Оказалось, что при изменении давления, вязкость некоторых жидкостей, таких как масла, может изменяться в несколько раз. А это уже определяет возможность использовать такие жидкости в качестве рабочей среды.

Источник

Давление в жидкостях и газах. Закон Паскаля.

теория по физике 🧲 гидростатика

Закон Паскаля: давление, производимое на жидкость или газ, передается жидкостью или газом во все стороны одинаково.

Такая особенность передача давления жидкостями и газами связана с подвижностью молекул в жидком и газообразном состояниях.

Давление столба жидкости определяется формулой:

p — давление столба жидкости (Па), ρ_ж— плотность жидкости (кг/м 3 ), g — ускорение свободного падения (≈10 м/с 2 ), h — высота столба жидкости, или ее глубина (м).

Важно! Высоту h нужно определять от поверхности жидкости.

Сила давления жидкости

Сила давления жидкости на дно сосуда — это произведение давления, оказываемого жидкостью на дно сосуда, на площадь этого дна:

Сила давления жидкости на боковую грань сосуда — это произведение половины давления, оказываемого жидкостью на дно сосуда, на площадь грани:

Подсказки к задачам:

Пример №1. Чему равно давление, созданное водой, на глубине 2 м?

Давление в жидкостях определяется формулой:

Давление, созданное пресной водой, равно:

p = 1000∙10∙2 = 20000 (Па) = 20 (кПа)

Давление, созданное соленой водой, равно:

p = 1030∙10∙2 = 20600 (Па) = 20,6 (кПа)

Гидростатический парадокс

Из закона Паскаля следует, что давление на дно сосуда определяется только плотностью жидкости и высотой ее столба. Поэтому, если в разные сосуды налить одинаковую жидкость одинаковой высоты, давление, оказываемое ею на дно каждого из сосудов, будет одинаковым.

Сила давления при этом будет разная, так как она прямо пропорционально зависит от площади дна. Так как площадь дна первого сосуда минимальна, а третьего максимальна, силы давления, оказываемые жидкостью на дно сосудов, будут такими:

F₁ 3 ), во втором — керосин (ρ₂ = 0,8 г/см 3 ), в третьем — спирт (ρ₃ = 0,8 г/см 3 ). В каком сосуде оказывается максимальное давление на дно?

Давление зависит только от плотности жидкости и от ее столба: площадь сосудов никакой роли не играет. Так как столбы жидкостей во всех сосудах одинаково, остается сравнивать плотности. Плотность воды больше плотности керосина и плотности спирта. Поэтому в сосуде 1 давление на дно сосуда будет максимальным.

Алгоритм решения

Решение

Запишем исходные данные:

Сила давления равна произведению давления на площадь, на которую это давление оказывается:

Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. А высота столба воды в данном случае равна разности высоту стакана и разнице между высотой сосуда и уровнем воды. Поэтому:

F = pS = ρ_жghS = ρ_жg(H – b)S = 1000∙10∙(0,2 – 0,02)∙0,01 = 18 (Н)

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем исходные данные:

Сила давления равна произведению давления на площадь, на которую это давление оказывается:

Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. Поэтому:

F = pS = ρ_кghS = 800∙10∙2∙0,001 = 16 (Н)

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке представлены графики зависимости давления p от глубины погружения h для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.

Выберите два верных утверждения, согласующихся с приведёнными графиками.

а) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.

б) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.

г) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.

Алгоритм решения

Решение

Проверим истинность первого утверждения (а). Для этого определим по графику давление воды на глубине 25 м. Если пустить перпендикуляр к графику зависимости давления воды от глубины погружения через h = 25 м, то он пересечет график в точке, которой соответствует давление p = 350 кН. Атмосферное давление равно 100 кН. Следовательно, давление воды на этой глубине в 3,5 раза превышает атмосферное давление. Утверждение неверно.

Проверим второе утверждение (б). Согласно ему, с ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде. Это действительно так, потому что угол наклона графика зависимости давления дийодметана от глубины погружения к оси абсцисс больше того же графика для воды. Это можно подтвердить и математически: давление в более плотной жидкости с глубиной растет быстрее, так как давление имеет прямо пропорциональную зависимость с глубиной. Утверждение верно.

Проверим третье утверждение (в). Согласно ему, если на этом же рисунке построить график зависимости давления керосина от глубины погружения, то он окажется между двумя уже существующими графиками. Но этого не может быть, потому что давление в воде растет медленнее, чем давление в дийодметане, так как вода менее плотная. По этой же причине давление в керосине будет расти медленнее, чем в воде, так как керосин менее плотный по сравнению с водой. Третий график в этом случае займет положение между графиком зависимости давления воды от глубины погружения и осью абсцисс. Утверждение неверно.

Проверим четвертое утверждение (г). Согласно графику, давление воды на глубине 10 м равно 200 кПа. Поэтому давление на поверхность шарика снаружи, погруженного на такую глубину, будет вдвое больше, чем давление, оказываемое на его стенки изнутри (при условии, что давление внутри равно 1 атм.). Утверждение неверно.

Проверим последнее утверждение (д). Согласно ему, если на этом же рисунке построить график зависимости давления оливкового масла от глубины погружения, то он окажется между графиком для воды и осью абсцисс. Это действительно так, потому что плотность оливкового масла меньше плотности воды. Утверждение верно.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Статика. Давление покоящейся жидкости на дно и стенки сосуда (гидростатическое давление).

Жидкости (и газы) передают по всем направлениям не только внешнее давление, но и то дав­ление, которое существует внутри них благодаря весу собственных частей.

Давление, оказываемое покоящейся жидкостью, называется гидроста­тическим.

Получим формулу для расчета гидростатического давления жидкости на произвольной глубине h (в окрестности точки A на рисунке).

Сила давления, действующая со стороны вышележащего узкого столба жидкости, может быть выражена двумя способами:

1) как произведение давления p в основании этого столба на площадь его сечения S:

2) как вес того же столба жидкости, т. е. произведение массы m жидкости на ускорение сво­бодного падения:

Масса жидкости может быть выражена через ее плотность p и объем V:

а объем — через высоту столба и площадь его поперечного сечения:

Подставляя в формулу (1.28) значение массы из (1.29) и объема из (1.30), получим:

Приравнивая выражения (1.27) и (1.31) для силы давления, получим:

Разделив обе части последнего равенства на площадь S, найдем давление жидкости на глубине h:

Это и есть формула гидростатического давления.

Гидростатическое давление на любой глубине внутри жидкости не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободно­го падения и глубины, на которой определяется давление.

Важно еще раз подчеркнуть, что по формуле гидростатического давления можно рассчитывать давление жидкости, налитой в сосуд любой формы, в том числе, давление на стенки сосуда, а так­же давление в любой точке жидкости, направленное снизу вверх, поскольку давление на одной и той же глубине одинаково по всем направлениям.

Гидростатический парадокс — явление, заключающееся в том, что вес жидкости, налитой в сосуд, может отличаться от силы давления жидкости на дно сосуда.

В данном случае под словом «парадокс» понимают неожиданное явление, не соответствующее обычным представлениям.

Так, в расширяющихся кверху сосудах сила давления на дно меньше веса жидкости, а в сужа­ющихся — больше. В цилиндрическом сосуде обе силы одинаковы. Если одна и та же жидкость налита до одной и той же высоты в сосуды разной формы, но с одинаковой площадью дна, то, несмотря на разный вес налитой жидкости, сила давления на дно одинакова для всех сосудов и равна весу жидкости в цилиндрическом сосуде.

Это следует из того, что давление покоящейся жидкости зависит только от глубины под свободной поверхностью и от плотности жидкости: p = pgh (формула гидростатического давления жидкости). А так как площадь дна у всех сосудов одинакова, то и сила, с которой жидкость давит на дно этих сосу­дов, одна и та же. Она равна весу вертикального столба ABCD жидкости: P = oghS, здесь S — площадь дна (хотя масса, а следовательно, и вес в этих сосудах различны).

Гидростатический парадокс объясняется законом Паскаля — способ­ностью жидкости передавать давление одинаково во всех направлениях.

Из формулы гидростатического давления следует, что одно и то же количество воды, находясь в разных сосудах, может оказывать разное дав­ление на дно. Поскольку это давление зависит от высоты столба жидкости, то в узких сосудах оно будет больше, чем в широких. Благодаря этому даже небольшим количеством воды можно создавать очень большое давле­ние. В 1648 г. это очень убедительно продемонстрировал Б. Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, подняв­шись на балкон второго этажа, вылил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давле­ние в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Источник

Давление в жидкости и газе. Расчет давления жидкости на дно и стенки сосуда

Решебник к сборнику задач по физике для 7- 9 классов, Перышкин А.В.

405. Поднимающиеся со дна водоема пузырьки воздуха увеличиваются в объеме по мере приближения к поверхности. Почему?
С приближением к поверхности, давление воды на пузырек падает.

406. Воду из узкого высокого стакана перелили в широкую кастрюлю. Как изменилось давление воды на дно?
Давление уменьшилось, поскольку уменьшилась высота водяного столба.

407. На рисунке 44 изображен старинный опыт: в крышку бочки, наполненную доверху водой, была вставлена высокая узкая трубка. Когда в трубку налили воды, бочка разорвалась. Объясните, почему небольшое количество воды, которую пришлось налить в трубку, могло разорвать бочку?

Давление на стенки бочки будет зависеть от плотности жидкости и высоты водяного столба и не зависит от площади поперечного сечения сосуда.

408. В сосуд налили слой воды высотой 15 см. каково давление этого слоя на дно сосуда?

409. Чему равно давление воды на глубине 50 см?

410. Банка высотой 50 см наполнена водою. Определите давление на 1 см2 дна банки.

412. Высота уровня воды в водопроводе 10 м (рис.45). Одинаковы ли давления на стенки трубы на различных высотах? Каково давление воды у нижнего конца трубы?

413. Каково давление на дверцу в шлюзовых воротах на глубине 12 м (рис. 46)?

414. В стакан высотой 10 см налита доверху ртуть. Вычислить давление на дно стакана.

415. Вычислите давление столбика ртути высотой 76 см.

416. Поршневой насос может произвести давление 5·105 Па. На какую высоту можно поднять воду этим насосом?

417. В трех сосудах налита вода до одной и той же высоты (рис. 47). В каком сосуде налито больше воды? В каком сосуде больше давление на дно?

Давление во всех сосудах на дно одинаково.

418. Внутрь жидкости погружен брусок (рис 48). Одинаковые ли давления испытывают боковые стенки бруска (левая и правая, передняя и задняя)? Одинаковые ли давления испытывают верхняя и нижняя грани бруска?

Боковые стенки испытывают одинаковое давление; верхняя и нижняя – разное.

419. Рассмотрите рисунок 48. Высота погруженного бруска АК=5 см. На сколько больше давление на грани MNKL, чем на ABCD, если брусок помещен в воду на глубину 12 см (до нижней грани)?

421. В сталелитейном производстве «изложницей» называется чугунный стакан без дна, в который выливают Расплавленный металл (рис. 49). Верхнее отверстие изложницы немного меньше нижнего для того, чтобы можно было изложницу снять с отвердевшего слитка, когда остынет металл. Чтобы металл снизу не выливался, изложницы ставят на плоское основание и делают их очень массивными. На рисунке 49 слева изображена изложница, справа — подъем изложницы с отлитого слитка.
Определите силу давления, которую производит на подложку изложницы налитый чугун, если высота изложницы 1,5 м, а площадь нижнего основания 1600 см2. Плотность чугуна 7,2 г/см3.

423. Для выпуска расплавленного металла из литейного ковша делают на дне ковша отверстие, закрываемое специальной пробкой из огнеупорного металла. Определите давление расплавленной стали на пробку, если высота налитого металла 2 м, а плотность расплавленной стали 7,3 г/см³.

424. Как велика должна быть высота столба ртути и столба спирта, если этот столб производит давление в 105 Па?

425. Определите давление воды на стенки котла водяного отопления, если высота труб 20 м?

426.Вычислите разность давлений в трубах водопровода на нижнем этаже здания и на этаже, расположенном выше на 15 м?

427. Батискаф спустился в море на глубину в 50 м. Каково давление на поверхность батискафа на данной глубине?

429. Давление в трубах водопровода 4·105 Па. На какую высоту будет бить вода из пожарной трубы, присоединенной к этому водопроводу, если не принимать во внимание сопротивление воздуха и трение воды в трубах?

430. Человек стоит на кожаном мешке с водой (рис. 51). Рассчитайте, на какую высоту поднимается вода в трубке, если масса человека 75 кг, площадь соприкасающаяся с мешком поверхности платформы 1000 см2.

Источник