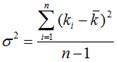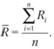Чем меньше дисперсия тем риск
Чем выше дисперсия (среднее квадратическое отклонение), тем больше риск, а более высокий риск значит большую доходность.
ФИНАНСОВАЯ СРЕДА И ПРЕДПРИНИМАТЕЛЬСКИЕ РИСКИ
ГЛАВА 7

· 
· 
Ожидаемый денежный выигрыш= (0,1*500)+(0,5*100)=100
Процентная доходнось  | Отклонения от ожидаемой доходности  -r -r | Квадрат отклонений (  ) 2 ) 2 | Вероятность | Вероятность* квадратическое отклонение |
| +500 | +400 | 0,1 | ||
| +100 | 0,5 | |||
| -100 | 0,4 |
Среднее квадратическое отклонение = корень из 20000=141
Задача 2. Вам выпал шанс сыграть на удачу, причем в игре возможны следующие проигрыши и выигрыши (см. табл. ниже). В каждом туре игры на кон нужно поставить 100 дол., так что чистый прибыток от игры — это выигрыш за вычетом 100 дол.
Каковы ожидаемый денежный выигрыш и ожидаемая доходность игры? Вычислите дисперсию и среднее квадратическое отклонение этой доходности.
Ответ:
Ожидаемая доходность выигрыша = 0,1*500+0,2*100+0= 100$
Ожидаемая доходность игры, следовательно, представляет собой средневзвешенную вероятных исходов: Ожидаемая доходность игры = 0,1*400+0-0,4*100=0
Стандартными статистическими показателями разброса исходов служат дисперсия и
среднее квадратическое отклонение. Дисперсия рыночной доходности представляет собой ожидаемое отклонение от ожидаемой доходности, возведенное в квадрат. Это можно выразить так:
Дисперсия = 0,1*500*400+0+0=20000
Среднее квадратическое отклонение =корень из 20000=141,42%.
Задача 3. В помещенной ниже таблице указаны значения номинальной доходности на мексиканском фондовом рынке и инфляции в Мексике.
А) Средняя арифметическая = 
Дисперсия = (14,56)^2+(9.16)^2+(-22.34)^2+(51.86)^2+(-53.24)^2=6318.94
Ср. кв. откл. = 
Реальная доходность =
0,109+0,17+0,46-0,18+0,75=1,309/5=0,26 
31,06/26=5,06 – съела инфляция
Задача 3. В помещенной ниже таблице указаны значения номинальной доходности на мексиканском фондовом рынке и инфляции в Мексике.
а) Какого среднее квадратическое отклонение рыночной доходности?
б) Подсчитайте среднюю реальную доходность.
А) Показателем разброса исходов служит дисперсия и среднеквадратическое отклонение. Дисперсия представляет собой ожидаемое отклонение от ожидаемой доходности, возведенной в квадрат.
В данной случае при подсчете дисперсии используем формулу:
Среднее квадратическое отклонение = Корень из 1461,1 = 38,22. Изменчивость доходности 38,22%.
Средняя реальная доходность = (1+ r ном) / (1+ инф) = (сред. доходность +1) / (1+ ср. инфляция) = 1,3106/1,2486 = 0,05 = 5% реальная доходность.
Лоуренс Менялоу— ведущий менеджер взаимного фонда, и с 1996 по 2000 г. ему удавалось обеспечивать следующую процентную доходность (в помещенной ниже таблице для сравнения указаны также значения доходности индекса S&P 500 за тот же период):
Вычислите среднюю доходность взаимного фонда м-ра Менялоу и ее среднее квадратическое отклонение. Как обстоят его дела по этим показателям: лучше или хуже, чем у индекса S&P 500?
Рассчитаем среднюю доходность (по формуле средней арифметической):
| Средняя доходность: | ||||||
| Менялоу | 16,1 | 28,4 | 25,1 | 14,3 | -6 | (16,1+28,4+25,1+14,3-6)/5=15,58 |
| S&P 500 | 23,1 | 33,4 | 28,6 | -9,1 | (23,1+33,4+28,6+21-9,1)/5=19,4 |
Вычислим разницу между показателями исходной процентной доходности и вычисленной средней:
| Менялоу | 16,1-15,58=0,52 | 12,82 | 9,52 | -1,28 | -21,58 |
| S&P 500 | 23,1-19,4=3,7 | 9,2 | 1,6 | -28,5 |
Возведем получившиеся показатели в квадрат и вычислим дисперсию:
| Дисперсия (σ 2 ): | ||||||
| Менялоу | (0,52) 2 =0,27 | 164,35 | 90,63 | 1,64 | 465,70 | (0,27+164,35+90,63+1,64+465,70)/5=144,52 |
| S&P 500 | (0,52) 2 =13,69 | 196,00 | 84,64 | 2,56 | 812,25 | (13,69+196+84,64+2,56+812,25)/5=221,83 |
Найдемсреднее квадратическое отклонение (σ) путем извлечения корня из дисперсии:
Для м-ра Менялоу:
Для S&P 500:
Таким образом, у фонда м-ра Менялоу средняя доходность меньше, чем у индекса S&P (15,6%
Задача 5. Лоуренс Менялоу— ведущий менеджер взаимного фонда, и с 1996 по 2000 г. ему удавалось обеспечивать следующую процентную доходность (в помещенной ниже таблице для сравнения указаны также значения доходности индекса S&P 500 за тот же период):
Вычислите среднюю доходность взаимного фонда м-ра Менялоу и ее среднее квадратическое отклонение.
Как обстоят его дела по этим показателям: лучше или хуже, чем у индекса S&P 500?
Ответ:
Средняя арифметическая = 
Дисперсия = (-0,5)^2+(-12,8)^2+(-9,5)^2+(1,28)^2+(21,58)^2=721,67
Ср. кв. откл. = 
Средняя арифметическая = 
Дисперсия = (-3,7)^2+(-14)^2+(-9,2)^2+(-1,6)^2+(10,3)^2=402,98
Ср. кв. откл. = 
Лучше
SP500 обстоят дела хуже так как 1, 03 меньше 1, 72
Глава 7. Задание 7.
В какой из следующих ситуаций вы добьетесь большего снижения риска, распределяя инвестиции между двумя видами акций?
а) Акции с совершенной корреляцией.
б) Корреляция отсутствует.
в) Умеренная отрицательная корреляция.
г) Совершенная отрицательная корреляция.
Ответ: г) Совершенная отрицательная корреляция.
При совершенной отрицательной корреляции всегда найдется портфельная стратегия (представленная определенным набором и соотношением разных акций в портфеле), позволяющая полностью исключить риск (например, поскольку среднее квадратическое отклонение у акций А в 1,86 раза превышает отклонение у акций Б, чтобы устранить риск портфеля из двух этих видов акций, нужно инвестировать в Б в 1,86 раза больше средств.). Очень жаль, что в реальной жизни такой совершенной отрицательной корреляции между обыкновенными акциями не бывает.
Для того чтобы вычислить дисперсию портфеля, состоящего из трех акций, нужно заполнить 9 ячеек. Используйте те же обозначения, какие мы применяли в этой главе: например, х1 — доля инвестиций в акции 1, s12 — ковариация акций 1 и 2, и т. д. Теперь заполните ячейки.








Моё пояснение:
Это пункт 7.3- вычисление портфельного риска.
Дисперсия для портфеля видов акций равна сумме значений в этих ячейках.
· X1, Х2, Х3- доли инвестиций в акции
· sij-ковариация доходности акций-мера совместной изменчивости 2х акций. 
В учебнике рассмотрен пример для 2х акций. Процедура строгая, заполняется по диагонали. Тогда по аналогии с ответом Брейли:
Итак,
1) Смотри зеленую линию на схеме:
Левая верхняя 
Средняя в точке пересечений цветов 
Правая нижняя 
* Содержание ячеек, расположенных по указанной диагонали, зависит от дисперсии акций
***** Обратите внимание, как заполнены остальные ячейки. Они идут от левого верхнего угла до правого нижнего (как бы огибая зеленую линию). Цветами обозначены одинаковые ячейки. Обозначения приведены выше.
! Все, что мы сделали, поможет вычислить в дальнейшем дисперсию портфеля. Затем извлечем корень и получим среднее квадратическое отклонение. Таким образом, мы смогли бы найти уровень риска портфеля акций.
Надеюсь, я смогла объяснить.J
Глава 7.
Задача 9.Предположим, среднее квадратическое отклонение рыночной доходности равно 20%.
а) Каково среднее квадратическое отклонение доходности диверсифицированного портфеля с бетой 1,3?
б) Каково среднее квадратическое отклонение доходности хорошо диверсифицированного портфеля с бетой 0?
в) Среднее квадратическое отклонение хорошо диверсифицированного портфеля составляет 15%. Чему равна его бета?
г) Среднее квадратическое отклонение плохо диверсифицированного портфеля равно 20%. Что вы можете сказать о его бете?
А. 1,3 * 0,2 = 0,26 или 26%- портфель из большого числа акций со средней β=1,3 фактически избавлен от влияния индивидуальных рисков, т.е. он воспроизводит практически все движения рынка.
В. β = среднее квадратическое отклонение доходности диверсифицированного портфеля/среднее квадратическое отклонение рыночной доходности = 0,15/0,20 = 0,75 – это говорит о том, что риск нашего портфеля в ¾ раза меньше, чем рыночный риск.
Г. β = 0,2/0,2 = 1,0 – портфель состоит из большого числа акций, средней риск по которым равен рыночному. Однако, т.к. у нас плохо диверсифицированный портфель, то β будет меньше 1,0. Это связано с тем, что индивидуальный риск присутствует, а из-за сильной связи между активами портфеля он способен снизить риск в целом по портфелю.
Задача 9. Предположим, среднее квадратическое отклонение рыночной доходности равно 20%.
А) Каково среднее квадратическое отклонение доходности диверсифицированного портфеля с бетой 1,3?
б) Каково среднее квадратическое отклонение доходности хорошо диверсифицированного портфеля с бетой 0?
в) Среднее квадратическое отклонение хорошо диверсифицированного портфеля составляет 15%. Чему равна его бета?
г) Среднее квадратическое отклонение плохо диверсифицированного портфеля равно 20%. Что вы можете сказать о его бете?
Ответ:
Г) риск портфеля по величине равен рыночному, часть его составляет индивидуальный риск. В
Дисперсия как мера финансового инвестиционного риска. Оценка дисперсии и среднеквадратического отклонения доходности ценных бумаг.
В статистике дисперсия или вариация является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания. В портфельной теории дисперсия доходности является мерой риска, связанного с инвестированием в определенный актив или портфель активов.
Если известен полный набор вероятностей исхода события, что крайне редко встречается на практике, для расчета величины дисперсии используется следующая формула:
где ki – доходность ценной бумаги или актива при i-ом варианте исхода событий;

pi – вероятность i-го варианта исхода событий.
В реальной практике инвестирования аналитику обычно доступны исторические данные о доходности ценной бумаги или актива. Если он располагает всем массивом информации, то есть оценивает дисперсию на основании генеральной совокупности данных, необходимо использовать следующую формулу:
где ki – i-ое значение доходности ценной бумаги;

n – количество наблюдений.
Однако чаще оценку риска проводят на основании некоторой выборки из генеральной совокупности данных, поэтому для получения несмещенной оценки дисперсии количество степеней свободы уменьшают на 1. В этом случае формула для ее оценки будет выглядеть следующим образом:
Чем выше значение дисперсии, то есть чем выше разброс доходности актива или портфеля активов относительно его ожидаемой доходности, тем выше будет уровень риска. Напротив, низкие значения этого показателя свидетельствуют о низком уровне риска, связанного с осуществлением инвестиций.
Также следует отметить, что квадратный корень от дисперсии случайной величины является ее среднеквадратическим отклонением.
Под риском можно понимать вероятность возникновения каких-либо отклонений от ожидаемого события. Основополагающими мерами риска финансового актива являются такие показатели, как стандартное отклонение (σ) и дисперсия (D = σ2) сто доходности. В качестве синонима понятия «стандартное отклонение» используют также термин «волатильность». Стандартное отклонение и дисперсия доходности актива отражают степень возможного разброса его фактической доходности вокруг его средней (наиболее вероятной) доходности. Данные меры риска можно определить на основе прошлых данных статистики доходности актива.
Доходность актива на рассматриваемом интервале определяется следующим образом:
где St-1 – стоимость актива в начале интервала наблюдения; St – стоимость актива в конце интервала наблюдения.
Пусть имеются значения доходности акции за п равных интервалов наблюдения. За первый интервал она составила величину R1, за второй – R2 и т.д., за п-й интервал – Rn
Средняя доходность актива за наблюдаемый период (R) рассчитывается по формуле
Дисперсия доходности актива определяется как мера разброса наблюдаемой доходности (в процентах) от ее математического ожидания (средней величины). Формула генеральной дисперсии имеет вид
В случае если количество наблюдений незначительно (меньше 30), то для получения несмещенной оценки рекомендуется использовать так называемую исправленную дисперсию:
Показателем, характеризующим относительный уровень риска финансового актива, является стандартное отклонение его доходности от ожидаемой (средней за период):
При этом оценка допустимого уровня стандартного отклонения является субъективной и характеризует готовность инвестора принимать риск с учетом возможной доходности финансового актива.
Дисперсия – это хорошо или плохо для инвесторов в акции?
Сама по себе дисперсия не является ни хорошо, ни плохо для инвесторов. Однако высокая дисперсия акций связана с более высоким риском и более высокой доходностью. Низкая дисперсия связана с меньшим риском и более низкой доходностью. Акции с высокой дисперсией, как правило, хороши для агрессивных инвесторов, которые менее склонны к риску, в то время как акции с низкой дисперсией, как правило, хороши для консервативных инвесторов, которые менее терпимы к риску.
Дисперсия – это мера степени риска вложения. Риск отражает вероятность того, что фактическая доходность инвестиций или их прибыль или убыток за определенный период будет выше или ниже ожидаемого. Есть вероятность, что часть или все инвестиции будут потеряны.
30-летний руководитель, поднимающийся по служебной лестнице с растущим доходом, обычно может позволить себе быть более агрессивным и менее склонным к риску при выборе акций. Инвесторы такого типа обычно хотят иметь в своем портфеле акции с высокой дисперсией. Напротив, 68-летний человек с фиксированным доходом, скорее всего, пойдет на другой тип компромисса между риском и доходностью, сосредоточившись вместо этого на акциях с низкой дисперсией.
Однако, согласно современной теории портфелей (MPT), можно уменьшить дисперсию без ущерба для ожидаемой доходности, комбинируя несколько типов активов посредством распределения активов. В соответствии с этим подходом инвестор создает диверсифицированный портфель, который включает не только акции, но и типы активов, такие как облигации, товары, инвестиционные фонды недвижимости или REIT, страховые продукты и деривативы. Диверсифицированный портфель может также включать, например, денежные средства или их эквиваленты, иностранную валюту и венчурный капитал.
Финансовые специалисты определяют дисперсию, вычисляя среднее значение квадратов отклонений от средней нормы прибыли. Стандартное отклонение затем можно найти, вычислив квадратный корень из дисперсии. В конкретный год инвестор может ожидать, что доходность акции будет на одно стандартное отклонение ниже или выше стандартной нормы доходности.
Дисперсия (вариация) | Variance
В статистике дисперсия или вариация (англ. Variance) является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания. В портфельной теории дисперсия доходности является мерой риска, связанного с инвестированием в определенный актив или портфель активов.
Формула
Если известен полный набор вероятностей исхода события, что крайне редко встречается на практике, для расчета величины дисперсии используется следующая формула:
где ki – доходность ценной бумаги или актива при i-ом варианте исхода событий;

pi – вероятность i-го варианта исхода событий.
В реальной практике инвестирования аналитику обычно доступны исторические данные о доходности ценной бумаги или актива. Если он располагает всем массивом информации, то есть оценивает дисперсию на основании генеральной совокупности данных, необходимо использовать следующую формулу:
где ki – i-ое значение доходности ценной бумаги;

n – количество наблюдений.
Однако чаще оценку риска проводят на основании некоторой выборки из генеральной совокупности данных, поэтому для получения несмещенной оценки дисперсии количество степеней свободы уменьшают на 1. В этом случае формула для ее оценки будет выглядеть следующим образом:
Интерпретации дисперсии
Чем выше значение дисперсии, то есть чем выше разброс доходности актива или портфеля активов относительно его ожидаемой доходности, тем выше будет уровень риска. Напротив, низкие значения этого показателя свидетельствуют о низком уровне риска, связанного с осуществлением инвестиций.
Также следует отметить, что квадратный корень от дисперсии случайной величины является ее среднеквадратическим отклонением.
Пример расчета
Пример 1. Предположим, что финансовому аналитику необходимо произвести оценку риска, связанного с приобретением акций Компании А и Компании Б. Предположим, что аналитику известен полный набор вероятностей событий, который представлен в таблице.
Ожидаемая доходность для акций Компании составит 18,75%, а для акций Компании Б 19,45%.

В свою очередь, дисперсия доходности акций Компании А будет равна 24,288%, а акций Компании Б 217,948%.
σ 2 А = (7-18,75)2*0,05 + (15-18,75)2*0,2 + (18-18,75)2*0,5 + (24-18,75)2*0,2 + (32-18,75)2*0,05 = 24,288%
σ 2 Б = (-24-19,45)2*0,05 + (8-19,45)2*0,2 + (20-19,45)2*0,5 + (31-19,45)2*0,2 + (57-19,45)2*0,05 = 217,948%
Хотя ожидаемая доходность у акций обеих компаний практически одинаковая, риски инвестирования в акции Компании Б будут существенно выше.
Пример 2. Историческая доходность акций за последние пять лет представлена в таблице.
Средняя доходность акции составит 5,784%.

Поскольку анализируется не вся генеральная совокупность данных, а только выборку из нее, оценка дисперсии составит 58,42%.
σ 2 = ((5,78-5,784)2 + (12,33-5,784)2 + (-7,21-5,784)2 + (8,25-5,784)2 + (9,77-5,784)2)/(5-1) = 58,42%