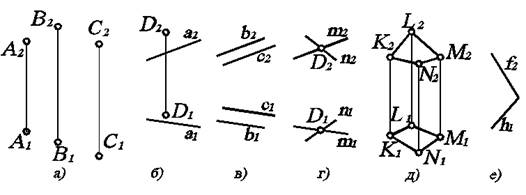
Чем может быть задана плоскость

Способы задания плоскости на чертеже

Положение плоскости в пространстве может быть однозначно определено одним из хорошо известных в геометрии элементов. В соответствии с этим плоскость может быть задана одним из шести способов:

а) тремя точками, не лежащими на одной прямой;

б) прямой и точкой, не лежащей на этой прямой;

в) двумя параллельными прямыми;

г) двумя пересекающимися прямыми;

Тогда на чертеже (рис. 3.1) соответствующие геометрические объекты (точки, прямые) выглядят в виде проекций.

Рис. 3.1. Безосный двухкартинный комплексный чертеж геометрических объектов, задающих плоскость.

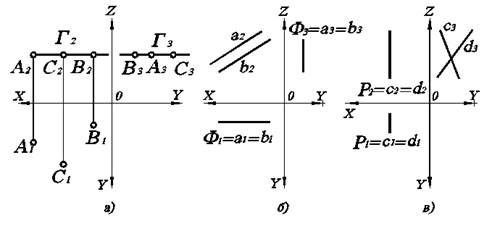
3.2. Плоскости частного и общего положения

3.2.1. Плоскости уровня

Плоскостью уровня называется плоскость, параллельная одной из плоскостей проекций, а следовательно, перпендикулярная двум другим. Тогда проекциями плоскости уровня будут прямые, параллельные соответствующим осям (рис. 3.2), вне зависимости от того, чем задана плоскость. От способа задания плоскости зависит лишь ее проекция на ту плоскость проекций, которой заданная плоскость параллельна.

Плоскость, параллельная П₂, называется фронтальной плоскостью уровня (Ф). Зададим ее параллельными прямыми (рис. 3.2б).

Плоскость, параллельная П₃, называется профильной плоскостью уровня (Р). Считаем ее заданной пересекающимися прямыми (рис. 3.2в).

Рис. 3.2. Плоскости уровня на комплексном чертеже.

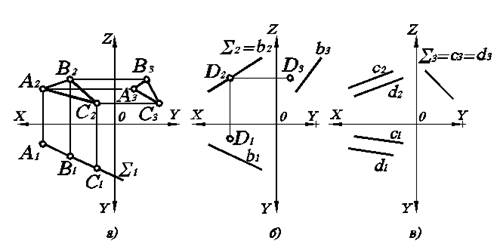
3.2.2. Проецирующие плоскости

Проецирующей называется плоскость, перпендикулярная одной из плоскостей проекций. Исходя из определения, такая плоскость вырождается в прямую при проецировании на ту плоскость проекций, к которой она перпендикулярна.

Рис. 3.3. Проецирующие плоскости на комплексном чертеже.

3.2.3.Плоскости общего положения

Плоскостью общего положения называется плоскость, не перпендикулярная и не параллельная ни одной из плоскостей проекций, а значит, расположенная под произвольным углом к каждой из них.

У такой плоскости все проекции будут плоские фигуры (рис. 3.4).

Рис. 3.4. Плоскость общего положения, заданная треугольником

3.3. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости. Принадлежность прямой плоскости определяется по одному из двух признаков:

а) прямая проходит через две точки, лежащие в этой плоскости;

б) прямая проходит через точку и параллельна прямой, лежащим в этой плоскости.

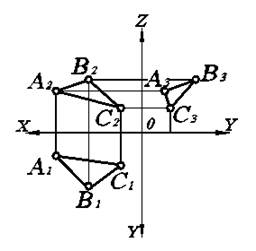
3.4. Главные линии плоскости

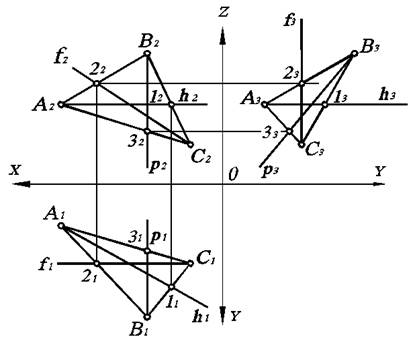
Главными линиями плоскости называются линии уровня, лежащие в данной плоскости. Рассмотрим построение главных линий плоскости, заданной треугольником (рис. 3.5).

Горизонталь плоскости DАВС начинаем с вычерчивания ее фронтальной проекции h₂, которая, как известно, параллельна оси ОХ. Поскольку эта горизонталь принадлежит данной плоскости, то она проходит через две точки плоскости DАВС, а именно, точки А и 1. Имея их фронтальные проекции А₂ и 1₂, по линии связи получим горизонтальные проекции 1₁. Соединив точки А₁ и 1₁, имеем горизонтальную проекцию h₁ горизонтали плоскости DАВС. Профильная проекция h₃ горизонтали плоскости DАВС будет параллельна оси ОХ по определению.

Профильная линия плоскости DАВС имеет горизонтальную р₁ и фронтальную р₂ проекции, параллельные осям OY и OZ, а профильную проекцию р₃ можно получить по фронтальной, используя точки пересечения В и 3 с D АВС.

При построении главных линий плоскости необходимо помнить лишь одно правило: для решения задачи всегда нужно получить две точки пересечения с данной плоскостью.

Рис. 3.5. Построение главных линий плоскости, заданной треугольником

3.5. Взаимное положение прямых и плоскостей

3.5.1. Параллельность прямых и плоскостей

Рис. 3.6. Построение параллельно расположенных геометрических объектов.

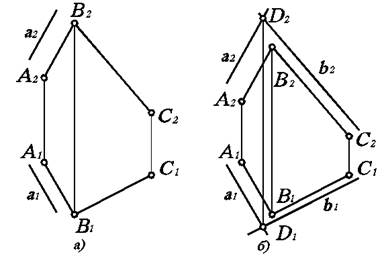
Тогда для построения параллельной прямой а (рис. 3.6а) необходимо, чтобы обе ее проекции были параллельны одноименным проекциям прямой (например, АВ), лежащей в данной плоскости. в) Плоскости параллельны друг другу, если две пересекающиеся прямые одной плоскости попарно параллельны двум пересекающимся прямым другой плоскости. Для интерпретации этого свойства достаточно дополнить построения на рис. 3.6а еще одной прямой в, пересекающей а и параллельной ВС (рис. 3.6б).

3.5.2. Перпендикулярность прямых и плоскостей

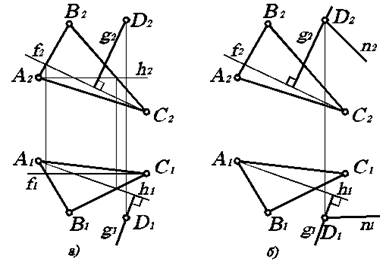
а). Прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, лежащим в этой плоскости, одна из которых фронталь, а другая горизонталь.

Рис. 3.7. Построение перпендикулярно расположенных геометрических объектов.

б). Плоскости перпендикулярны друг к другу, если одна из них содержит перпендикуляр к другой.

Обратимся к рис. 3.7а, где перпендикуляр g к плоскости уже построен, необходимо через точку D провести произвольную прямую q (рис. 3.7б).

3.6. Позиционные задачи на плоскости

Позиционными называются задачи на определение каких-либо общих элементов геометрических объектов, например, точки пересечения прямой и плоскости, линии пересечения двух плоскостей.

3.6.1. Пересечение прямой и плоскости

Задачу на пересечение прямой и плоскости можно решать с помощью вспомогательной секущей плоскости, которая должна удовлетворять следующим условиям:

а) быть плоскостью частного положения, так как именно плоскость частного положения проецируется на соответствующую плоскость проекций в виде прямой;

б) проходить через прямую, точку пересечения которой с плоскостью мы отыскиваем.

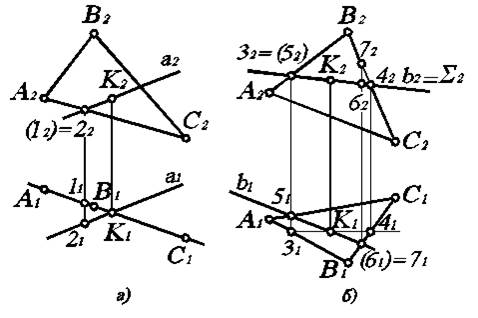
Осталось определить видимые участки прямой а, поскольку на П₂ часть указанной прямой будет закрыта от наблюдателя плоскостью DАВС. Для этого необходимо рассмотреть точку, где пересекаются фронтальные проекции а и какой-либо прямой ( например, АС ), лежащей в плоскости DАВС. Обозначим эту точку 1₂. Но пересекаться прямая а и DАВС могут только в одной точке, которую мы отыскали (К₂). Все остальные точки будут точками, где они скрещиваются. Следовательно, прямая а и АС скрещиваются в пространстве. Значит, все точки, где пересекаются их проекции, будут конкурирующими, а именно 1₂=2₂. Тогда на П₁ имеем по линии связи 1₁ÎА₁С₁ и 2₁ Î а₁. Видимой является точка 2, которая принадлежит прямой а. Это сохраняется до точки пересечения К₂. Затем, естественно, участок прямой а будет невидим (обозначается пунктирной линией) до выхода из-под плоскости DАВС. Теперь задачу можно считать полностью решенной.

Рассмотрим общий случай пересечения прямой и плоскости, когда обе они занимают общее положение в пространстве. Пусть плоскость задана треугольником DАВС. Здесь и в дальнейшем используем задание плоскости в основном треугольником, так как в этом случае решение задачи наиболее наглядно. Необходимо найти точку пересечения произвольно заданной прямой в с DАВС (рис. 3.8, б).

Рис. 3.8. Пересечение прямой и плоскости

Определим видимые участки прямой в на обеих проекциях по конкурирующим точкам. Для определения видимости на П₂ используем фронтально-конкурирующие точки (например, точки 3₂=5₂, где скрещиваются в₂ и А₂В₂). Очевидно, что точка 3₁ ближе к нам, чем точка 5₁. Следовательно, на П₂ выше 3₂, тогда в этой точке А₂ В₂ выше, а в₂ лежит под ней. Это верно только до точки пересечения К₂. Далее, естественно, выше будет в₂. Аналогично по горизонтально–конкурирующим точкам (например, 6₁=7₁) определяем, что в точках 6₁=7₁ прямая В₁С₁ лежит выше, чем в₁, так как точка 7₂ расположена выше, чем точка 6₂. Невидимый участок прямой в обозначаем пунктирной линией.

3.6.2. Пересечение плоскостей. Метод вспомогательных секущих плоскостей

Поскольку линией пересечения двух плоскостей является прямая, то для ее построения необходимо определить лишь две точки пересечения плоскостей.

Для решения указанной задачи применяется метод вспомогательных секущих плоскостей, который заключается в следующем.

Вводятся две дополнительные плоскости, пересекающие заданные. Для каждой дополнительной (вспомогательной) плоскости строим линию ее пересечения с заданными плоскостями. Точка пересечения двух полученных линий и будет точкой пересечения заданных плоскостей. Поскольку дополнительных плоскостей две, то и точек пересечения заданных плоскостей тоже две. Соединяя их, получаем линию пересечения плоскостей. Разумеется, каждая дополнительная плоскость должна занимать частное положение в пространстве, тогда на плоскость проекций, к которой вспомогательная плоскость перпендикулярна, она проецируется в прямую. Иначе, если вспомогательная плоскость занимает общее положение, введение дополнительной плоскости не упрощает решение задачи.

Проиллюстрируем на двух примерах.

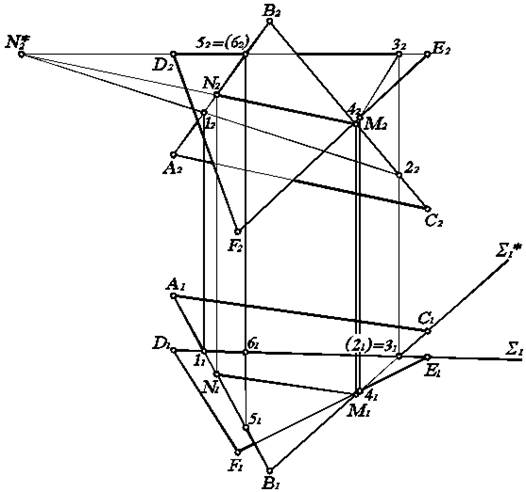
Найти линию пересечения двух треугольников АВС и DEF и определить видимость сторон (рис. 3.9). Построим линию пересечения треугольников, воспользовавшись методом дополнительных секущих плоскостей. Для упрощения решения задачи секущие плоскости будем проводить через стороны треугольников.

Рис. 3.9. Пересечение двух треугольников

Пусть дополнительная горизонтально–проецирующая плоскость S проходит через сторону DE. Тогда S₁= D₁E₁. Это и есть горизонтальная проекция линии пересечения S с DАВС и DDEF. Построим фронтальную проекцию. Для DDEF таковой является, очевидно, D₂E₂. Для DАВС по горизонтальным проекциям 1₁ и 2₁ точек пересечения найдем их фронтальные проекции 1₂ и 2₂, соединив которые, получим фронтальную проекцию линии пересечения плоскости S и DАВС. Продлив линии D₂E₂ и 1₂ 2₂, найдем точку их пересечения N₂*, которая и является точкой пересечения плоскостей, заданных треугольниками. Надо заметить, что точка N₂* не принадлежит треугольникам, поэтому и является точкой пересечения не треугольников, а плоскостей, в которых лежат треугольники.

Аналогично, вводя дополнительную горизонтально–проецирующую плоскость S*, проходящую через сторону ВС треугольника АВС, найдем точку М₂ пересечения заданных треугольников.

Дата добавления: 2017-04-05 ; просмотров: 18857 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф Ф.,

2.5. Плоскость. Способы задания плоскости на комплексном чертеже

Плоскость, простейшая поверхность [5]. Понятие плоскость (подобно точке и прямой) принадлежит к основным понятиям геометрии. Плоскость обладает свойством, что любая прямая, соединяющая две точки плоскости, принадлежит плоскости.

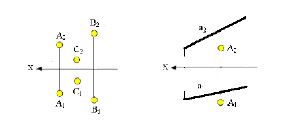
Плоскость на комплексном чертеже однозначно могут определить три точки не расположенные на одной прямой (рис. 2.12 а), прямая и точка, не принадлежащая ей (рис. 2.12 б).

Рис. 2.12. Изображение плоскости, заданной: а – тремя точками; б – точкой и прямой линией

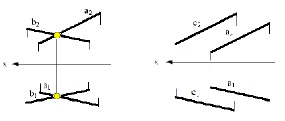
Плоскость на комплексном чертеже можно задать двумя пересекающимися прямыми (рис. 2.13 а) или двумя параллельными прямыми (рис. 2.13 б).

Рис. 2.13.Изображение плоскости, заданной: а – двумя пересекающимися прямыми; б – двумя параллельными прямыми

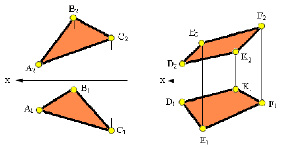
На комплексном чертеже плоскость может быть задана плоской фигурой. На рис. 2.14. а изображён комплексный чертёж, на котором представлена плоскость, заданная плоскостью треугольника. На рис. 2.14 б представлен комплексный чертёж, на котором изображена плоскость, заданная многоугольником.

Рис. 2.14. Изображение плоскости заданной: а – плоскостью треугольника; б – плоскостью многоугольника

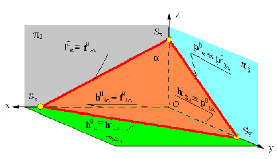
В начертательной геометрии существует ещё один способ задания плоскости на комплексном чертеже – следами. Этот способ обладает преимуществом перед другими вариантами ее изображения на эпюре потому, что сохраняется наглядность изображения и требуется указать только две прямые вместо четырех или шести.

Рис. 2.15. Способ задания плоскости следами плоскости

На рисунке 2.15 показана плоскость общего положения, заданная следами f0, h0, p0, которые расположены, по отношению к плоскостям проекций, под углами, отличными от 90°, но при этом они параллельны соответствующим плоскостям проекций и являются частным случаем изображения линий уровня представленной на рисунке плоскости. Это свойство можно использовать при решении геометрических задач. На рассматриваемом рисунке фронтальный след плоскости α(f0,h0,p0) параллелен фронтальной проекции фронтали этой плоскости f0║f2, горизонтальный след плоскости α(f0,h0,p0) параллелен горизонтальной проекции горизонтали этой плоскости h0║h1,профильный след плоскости α(f0,h0,p0) параллелен профильной проекции профильной прямой этой плоскости p0║p3.

Источник

Лекция 3. Плоскость

3.1. Способы задания плоскости на ортогональных чертежах

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

Плоскость общего положения может иметь три следа: горизонтальный – απ₁, фронтальный – απ₂ и профильный – απ₃, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π₁, фронтальной π₂ и профильной π₃ (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

Рисунок 3.6 – Принадлежность прямой плоскости

\left.\begin\alpha=m\parallel n,\\D\in\alpha\\C\in\alpha\\\end\right\> \Longrightarrow CD\in\alpha

Упражнение

Рисунок 3.7 – Решение задачи

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π₁) (Рисунок 3.8, а; 3.9).

Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π₂) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π₃) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

\alpha=m\cap n\\\left.\begina_2\parallel m_2\\a_1\parallel m_1\\\end\right\> \Rightarrow a\parallel\alpha

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Упражнение

Заданы: прямая АВ общего положения, плоскость σ⊥π₁. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.

Рисунок 3.15 – Пересечение прямой с плоскостью

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π₁ или π₂.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π₂ (рис. 3.15)
Выберем точки, конкурирующие на π₂ – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π₂ надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π₂.
Направление взгляда на π₂ показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π₂, видно, что точка 4₁ располагается ближе к наблюдателю, чем 3₁.
4₁∈E₁F₁ ⇒ 4∈EF ⇒ на π₂ будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π₁.
Для определения видимости выберем точки, конкурирующие на π₁ – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π₁ надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π₁.
Направление взгляда на π₁ показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π₁, видно, что точка 2₂ располагается ближе к наблюдателю, чем 5₂.
2₂∈А₂В₂ ⇒ 2∈АВ ⇒ на π₁ будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Упражнение

Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Упражнение

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Упражнение

Алгоритм решения задачи :

\left.\beginAB\cap\sigma=K\\AC\cap\sigma=L\\\end\right\> \left.\begin\Rightarrow A_1B_1\cap\sigma_1=K_1 \rightarrow K_2\\\Rightarrow A_1C_1\cap \sigma_1=L_1 \rightarrow L_2\\\end\right.

KL – линия пересечения ΔАВС и σ (α∩σ = KL).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Упражнение

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи :

\left.\begin\alpha\cap\sigma=(4-5)\\\beta\cap\sigma=(3-2)\\\end\right\>\\\left.\begin\alpha\cap\tau=(6-7)\\\beta\cap\tau=(1-8)\\\end\right\>\left.\begin(4_1-5_1)\cap(3_1-2_1)=M_1\rightarrow M_2\\(6_1-7_1)\cap(1_1-8_1)=N_1\rightarrow N_2\\\end\right\>\rightarrow\\\left.\beginM_1N_1\\M_2N_2\\\end\right\>\Rightarrow\alpha\cap\beta=MN

Упражнение

Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π₂, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π₂ (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.

3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Упражнение

Задана плоскость σ⊥π₂ и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C₁D₁ должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС

3.9. Задачи для самостоятельного решения

1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.

Постройте фронтальную проекцию точки К.

2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π₂, если его диагональ MN //π₂ (Рисунок 3.26).

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π₁.

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π₁.

Источник