Что нужно сделать чтобы найти 2 множитель в уравнении
Как найти множитель
Как найти неизвестный множитель? Способ первый — применить правило нахождения неизвестного множителя:
Как быть, если нужно решить уравнение, а правило позабылось? В этом случае можно придумать пример на умножение, чтобы разобраться с его помощью, что следует сделать, чтобы найти множитель, и так же найти неизвестный множитель в своем уравнении.
Как найти неизвестный первый множитель — 2? Надо 6 разделить на 3. Вывод: чтобы найти первый множитель, нужно произведение разделить на второй множитель.
Как найти второй множитель — 3? Надо 6 разделить на 2. Значит, чтобы найти второй множитель, нужно произведение разделить на первый множитель.
Так как от перемены мест множителей произведение не меняется, для нахождения неизвестного множителя порядок множителей можно не учитывать.
Рассмотрим на примерах, как найти неизвестный множитель.
1)
| 8 | · | x | = | 72 |
| 1мн. | 2мн. | пр. |
Чтобы найти неизвестный множитель, делим произведение на известный множитель:
| y | · | 10 | = | 280 |
| 1мн. | 2мн. | пр. |
Чтобы найти множитель, надо произведение разделить на известный множитель:
Более сложные примеры, в которых умножение — только одно из действий, мы рассмотрим позже.
Что такое множитель и разложение на простые множители
Дадим определение понятию «множитель» и разберемся что такое множитель. Какие множители бывают и почему некоторые из множителей — простые.
Определение множителя
В младших классах вы учили, что множители — это числа, которые мы умножаем, называя результат их умножения произведением.
Определения множителя как компонента умножения
Сейчас немного расширим понятие множителя.
Давайте рассмотрим определение множителя на примерах. Давайте определим где в представлении числа или выражения прячется множитель?
Пример 1
Пусть нам дано число 15. Это число можно представить в виде произведения 
. Значит, согласно определению 5 — это множитель, 3 — это тоже множитель.
Пример 2
Рассмотрим теперь выражение: 
. Это выражение можно представить в виде произведения 
. Получаем два множителя — первый множитель (2x-3) и второй множитель (2x+3).
Самое простое произведение имеет два множителя, но может быть и больше множителей.
Простые множители
Пример 1
Разложите число 65 на простые множители.
Решение: число 65 будем делить на простые числа, пока оно нацело не разделится. Так мы видим, что число 65 не делится на 2, 3 и 4, так как не соответствует признакам делимости на эти числа. Зато делится на 5, так как оканчивается на 5. При делении мы получаем 13. Число 13 — простое, так как делится только на себя и на единицу. Таким образом, число 
. И мы выполнили разложение числа на простые множители. Теперь вы знаете, как разложить число на простые множители.
Пример 2
Разложите число 270 на простые множители.
Решение: Разделим сначала число 270 на 2 (сначала берем самое маленькое простое число), получим 135. Посмотрим, делится ли это число на 3. Для этого сложим все числа, стоящие в разрядах данного числа — 
. Девять делится на 3, значит, и число 135 разделится на 3: 
. Получившееся число опять делится на 3: 
. И снова число 15 делится на 3: 
. Получили простое число 5. Делим 
.
Итак, запишем разложение числа 270 на простые множители в виде столбца, где справа от черты мы пишем на какое простое число мы делим, а слева — что получаем:
Разложение числа на простые множители в столбик.
Разложение числа на простые множители в строчку записывается так: 
.
Про разложение многочлена на множители поговорим в отдельной теме.
Нахождение неизвестных множителя, делимого или делителя
Урок 23. Математика 4 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Нахождение неизвестных множителя, делимого или делителя»
Множитель, множитель, произведение. Делимое, делитель, частное.
Сегодня у нас непростой урок, ведь нам предстоит разобраться, как находить неизвестные: множитель, делимое или делитель. А для чего это надо уметь? Догадались? Ну конечно для того, чтобы уверенно решать уравнения! И мы, конечно же, решим несколько уравнений. Но прежде надо кое-что вспомнить.
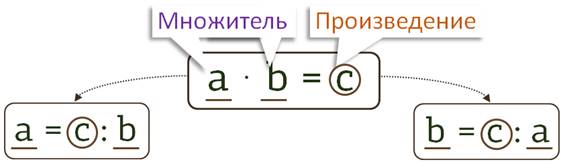
Я предлагаю вам посмотреть на буквенную запись действия умножения.
А и Б в этой записи являются множителями, Ц – произведением. Понятно, что произведение мы получаем действием умножения. Это – целое, то есть наибольшее число. А вот множители являются частями. Значит, их мы находим обратным действием, делением.
То есть, если нужно найти неизвестный множитель, мы произведение делим на известный множитель.
А теперь посмотрим на буквенную запись деления:
Обычно, целое можно разделить на части. Поэтому К, делимое, является целым, а М и Н – это части. И, естественно, что целое мы находим умножением. Поэтому, если надо найти неизвестное делимое, мы перемножаем делитель с частным.
А вот делитель является частью. И, если надо найти неизвестный делитель, то его мы найдём, разделив делимое на частное.
Ну а теперь пришло время решать уравнения. Давайте разберём вот это уравнение:
Посмотрите, это у нас осложнённое уравнение. Поэтому, прежде всего, надо его упростить, то есть, выполнить действие в правой части уравнения. Сто двадцать шесть разделить на два равно шестьдесят три. Переписываем уравнение, заменив действие деления на его результат. Здесь надо найти неизвестный множитель. Чтобы найти неизвестный множитель, мы произведение делим на известный множитель.
Шестьдесят три делим на девять, получается семь.
Не забываем выполнить проверку уравнения. Сначала переписываем его, заменив икс на его значение, которое мы получили – семь. Семью девять – шестьдесят три. Сто двадцать шесть разделить на два – шестьдесят три. Левая и правая части уравнения равны, значит, уравнение решено верно. Решаем следующее уравнение:
Неизвестное делимое находим умножением.
Ну, а следующее уравнение я предлагаю вам решить самостоятельно.
Какой компонент здесь надо найти? Неизвестный делитель. А его мы находим
Проверьте, ребята, так ли решено у вас уравнение?
Видите, как помогает при решении уравнений знание правил.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, надо делитель умножить на частное.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Выучите их, ребята, и не забывайте пользоваться при решении уравнений. Пока! До новых встреч!
Решение простых линейных уравнений
Понятие уравнения
Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.
В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
