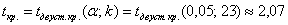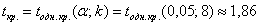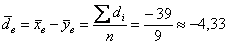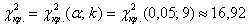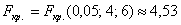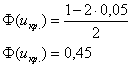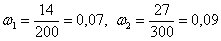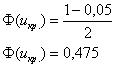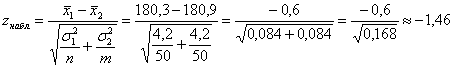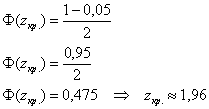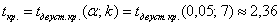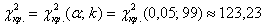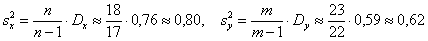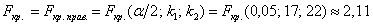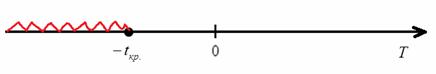Что нужно сделать чтобы проверить гипотезу
Мир статистических гипотез
В современном мире мы обладаем все большим и большим объемом данных о событиях, происходящих вокруг. Зачастую у нас появляются вопросы, на которые хотелось бы быстро ответить на основе имеющейся информации, для этого как нельзя лучше подходит процесс, связанный с проверкой статистических гипотез. Однако, многие считают, что это занятие подразумевает под собой большое число вычислений и в принципе довольно сложно для понимания. На самом деле, алгоритм проверки гипотез достаточно прост, а для осуществления расчетов с каждым годом появляется все больше и больше готовых инструментальных средств, не требующих от человека глубоких познаний в области. Далее я попытаюсь показать, что мало того, что процесс проверки гипотез может быть полезным, так и осуществляется достаточно быстро и без серьезных усилий.
Статистические гипотезы и области их применения
Проверка статистических гипотез является важнейшим классом задач математической статистики. С помощью данного инструмента можно подтвердить или отвергнуть предположение о свойствах случайной величины путем применения методов статистического анализа для элементов выборки. Если в предыдущем предложении какие-либо термины являются не совсем понятными, ниже можно найти пояснение на простом языке.
Для проверки статистических гипотез зачастую применяются статистические тесты, о которых будет рассказано далее.
Алгоритм проверки статистической гипотезы
В обобщенном виде алгоритм выглядит таким образом:
Формулировка основной (H0) и альтернативной (H1) гипотез
Выбор уровня значимости
Выбор статистического критерия
Определения правила принятия решения
Итоговое принятие решения на основе исходной выборки данных
Данные шаги являются унифицированными и схему можно использовать почти во всех случаях. Далее подробнее рассмотрим пример работы данного алгоритма на конкретных данных.
Пример проверки статистической гипотезы
Итак, как вы, наверное, догадались по вышеприведенным примерам, будем проверять гипотезу о том, что имеется существенное различие между числом созданных европейских AI-стартапов в 2019-м и 2020-м годах. Пример достаточно простой, чтобы было проще разобраться в ходе работы алгоритма.
Проверка гипотезы о законе распределения
Для данных 2019-го года проверим нормальность распределения.
H0: случайная величина распределена нормально
H1: случайная величина не распределена нормально
Пусть уровень значимости alpha = 0.05 (как и в 95-ти процентах статистических тестов). Определение уровня значимости достойно отдельного поста, так что не будем заострять на нем внимание.
Будет использован критерий Шапиро-Уилка.
,
,
,
;
Можно сравнить статистику W с критическим значением Wкрит. Критическое значение чаще всего приведено в готовых таблицах (по строкам/столбцам там отмечен объем выборки и уровень значимости, а на пересечении как раз-таки и лежит Wкрит.). Если W>Wкрит., то не отвергаем H0 и наоборот. Но это не очень удобно, поэтому чаще используется второй способ.
Разнообразие статистических критериев
Как мы увидели на примере, важным шагом в проверке статистической гипотезы является выбор критерия. В примере выше я использовала лишь два статистических критерия, но по факту их гораздо больше, так сказать, на все случаи жизни. Данные критерии важно знать и четко нужно осознавать, когда и какой можно применить. Многие из них направлены на сравнение центров распределений случайных величин, например, сравнение средних, медиан, равенство параметра распределения какому-либо числу и т. д. В основном они делятся на параметрические (знаем закон распределения случайной величины) и непараметрические.
Для вашего удобства внизу (рис. 3) приведена таблица с основными, с моей точки зрения, критериями сравнения центров распределения и их классификацией. Надеюсь, она будет вам полезна, ее можно дополнять и расширять по вашему желанию.
Формирование гипотез, запуск A/B-теста и анализ его результатов
Команда аналитиков компании AIC рассказала о принципах A/B-тестирования.
A/B-тестирование — обязательный подход к проверке продуктовых гипотез. Сегодня сложно удивить менеджера или аналитика тем, что организация проводит A/B-тесты на постоянной основе. Крупнейшие ИТ-компании инвестируют большие суммы в формирование отдельных команд, которые занимаются развитием платформ для запуска A/B-тестов, поиском и внедрением новых методик анализа результатов A/B-тестов.
Грамотное и плодотворное A/B-тестирование — это не просто разделение трафика на равные и неравные доли и оценка нескольких чисел в онлайн-калькуляторе. Это совокупность целого ряда статистических методов — тех самых, о которых вы читали в учебниках и изучали в университете.
В этой статье мы пошагово рассмотрим подход AIC к проведению А/В-тестирования — от процесса формирования гипотез до анализа результатов A/B-теста и их интерпретаций.
Важно: все примеры показаны на открытых dataframe. Пожалуйста, отнеситесь к этому с пониманием — мы не можем распространять реальные данные компаний.
Хорошая гипотеза рождается на стыке качественных и количественных данных. Большие данные покажут вам, где болит, а качественные погрузят в контекст проблемы.
Качественные данные указывают исследователю на проблемы реальных пользователей, которые обязательно должны быть подкреплены количественными показателями. Иначе можно столкнуться с тем, что мы начнем решать проблемы одного пользователя и упустим действительно важные вещи.
Процесс формирования гипотез начинается со знакомства с количественными данными. На этом этапе аналитики исследуют поведение пользователей, выявляют особенности продукта и находят узкие места.
Количественные данные собирают в следующие структуры:
Воронка — самое наглядное представление линейного движения пользователя по направлению к целевому действию. Она доступна для понимания даже тем, кто никогда не сталкивался с анализом данных: в простой форме воронка показывает поведение пользователей и выявляет самые проблемные шаги.
Стоит отметить, что самая частая ошибка при построении воронки — отсутствие разделения на сегменты. Допуская такую ошибку, вы рискуете упустить из вида проблемы отдельных групп пользователей.
Представление данных в динамике.
Важно учитывать динамику поведения пользователей в зависимости от дней, недель, месяцев или любых других периодов, которые подходят под бизнес-цикл вашего продукта. Основная ценность метода в том, что он позволяет отличить случайные колебания в данных от статистически значимого роста и падения ключевых метрик.
Не все пользователи, пришедшие на продукт, сразу же совершают целевое действие, будь то заполнение анкеты, покупка товара или приобретение услуги. Уход человека с одного из шагов воронки еще не говорит о наличии проблемы. Скорее всего, клиент просто ушел подумать или поискать альтернативные предложения. Построение когорт способно показать реальную картину прохождения воронки и возвращения пользователей на отдельные этапы. При построении когорт также важно проводить сегментацию.
Сценарии или нелинейные воронки.
Пользователи в продукте ведут себя нелинейно. И чаще всего их реальное поведение оказывается совершенно не таким, как мы себе представляем. Построение сценариев переходов на основе реальных данных помогает трезво посмотреть на поведение аудитории.
Данные по результатам исследований.
После того, как узкие места продукта выявлены, самое время приступить к подробному исследованию найденных проблем. Для этого нужно подобрать оптимальный набор количественных и качественных методов.
Среди них — очные и удаленные юзабилити-исследования, глубинные интервью, включенные наблюдения и прочее. Методов много, поэтому в процессе их выбора важно исходить из бизнес-задачи и не браться за все подряд. Этой теме мы посвятим отдельную статью в скором времени.
После того, как собраны все необходимые данные, можно приступать к формированию и приоритизации гипотез.
Список сформулированных гипотез может получиться очень большим, поэтому он требует приоритизации и определения периодов запуска экспериментов. Для ранжирования гипотез существует несколько методов, среди них — PIE, CXC и другие. Подробнее о приоритете мы расскажем в отдельной статье.
На практике часто приходится работать с продуктами с долгим и сложным циклом разработки. У клиентов практически не остается времени на проработку гипотез, их реализацию и запуск экспериментов, поэтому эту часть работ мы берем на себя.
Для запуска экспериментов мы чаще всего используем GTM или Google Optimize, где разделяем трафик, готовим визуальное представление гипотезы и задаем условия ее отображения (сегменты и тому подобное). В результате мы получаем возможность менять не только цвет и тексты, но и создавать новые функциональные сущности или развивать имеющиеся, а также успешно сегментировать гипотезы еще на этапе запуска. Это дает большое преимущество в условиях ограниченных технических и финансовых ресурсов.
A/B-тестирование — это чистая статистика. Примитивно использовать онлайн-калькулятор для анализа результатов теста, потому что появляется высокий риск ошибки. В этом случае не учитываются особенности данных в динамике.
Для уверенности в достоверности полученных результатов нужно комплексно подходить к процессу анализа. Грамотный процесс аналитики должен содержать в себе шесть этапов.
Первый важный этап анализа данных эксперимента — расчет вариации данных внутри экспериментальных выборок. Чтобы считать данные пригодными для анализа, нужно убедиться, что уровень вариации случайной величины находится в допустимых пределах.
Построение графиков box-plot дает наглядное представление о дисперсии данных внутри групп, наличии или отсутствии выбросов и уровне средней медианы.
Нижняя и высшая точка каждого box-plot представляет наименьшее и наибольшее наблюдаемые значения. Нижняя и верхняя границы широкой части — это вторая и третья квартиль, а линия внутри — медиана. Если на графике присутствуют точки, лежащие за пределами основного тела графика, то в выборке присутствуют выбросы.
Параллельно с построением box-plot рассчитываются основные описательные статистики по целевым действиям (шагам воронки). Для этого в R используется библиотека psych, позволяющая посчитать все описательные статистики для каждой переменной внутри переданного на вход dataframe.
Если эксперимент проходил в течение достаточного количества времени, а собранные данные обладают допустимым уровнем вариации, то распределение чаще всего оказывается нормальным. В любом случае важно точно выявить закон распределения пользователей, чтобы подобрать соответствующие методы оценки достоверности результатов.
Расчет критерия Бартлета, или коэффициента гомогенности дисперсии позволяет выявить разницу межгрупповых дисперсий по всем веткам эксперимента.
Обработка данных делается для понимания природы самих данных и для уверенного выбора метода оценки результатов.
В зависимости от ситуации мы используем несколько методов оценки: критерий Мана-Утни, однофакторный дисперсионный анализ и дисперсионный анализ по Краскелу-Уолису.
Основы науки о данных — A/B тестирование
Если вы уже имели дело со статистикой, вы возможно задавались вопросом: «Разве A/B тестирование не тоже самое, что проверка статистических гипотез?». Так и есть! Поэтому давайте узнаем побольше об A/B тестировании, разобрав на простом примере принцип работы проверки статистических гипотез.
Представьте, что наш клиент — владелец очень успешного приложения для работы с личными финансами. Он обратился к нам со следующей проблемой:
Тони, новый дизайн нашего приложения должен помочь пользователям сэкономить больше денег. Но приводит ли он к этому на самом деле? Пожалуйста помоги нам определить это, чтобы мы могли принять решение о внедрении этого дизайна.
Наша цель — определить, экономят ли пользователи лучше благодаря новому дизайну приложения. Для начала, нам надо узнать, имеем ли мы необходимое нам количество данных, поэтому мы задаем вопрос: «Какие потенциально полезные данные вы уже собрали?»
Оказывается, наш клиент уже провел эксперимент и собрал некоторые данные:
Шесть месяцев назад, наш клиент выбрал 1000 новых пользователей и разделил их на две группы: 500 в контрольной группе и 500 в экспериментальной группе.
Через шесть месяцев, наш клиент фиксирует процент экономии всех 1000 пользователей. Процент экономии (дословно «норма сбережений») представляет собой процент, который конкретный пользователь экономит от расчетного чека за каждый месяц. Наш клиент узнает следующую информацию:
Результаты нашего эксперимента на гистограмме выглядят следующим образом:
Создается впечатление, что по окончании шести месяцев представители экспериментальной группы имели более высокий процент экономии, чем представители контрольной группы. Можем ли мы просто построить данную гистограмму, показать её клиенту и считать работу законченной?
Нет, потому что мы не можем быть уверены в том, что данный рост экономии был вызван новым дизайном. Возможно, нам просто не повезло при выборе пользователей для эксперимента, и все люди с желанием экономить больше попали в экспериментальную группу.
Для решения этой проблемы нам необходимо задать следующий вопрос:
Какова вероятность того, что данный результат мы получили только из-за случайного стечения обстоятельств?
Суть проверки статистических гипотез (и А/В тестирования) как раз и заключается в ответе на данный вопрос.
Давайте представим альтернативную ситуацию, в которой новый дизайн не помог пользователям экономить лучше. Даже в таком случае, несмотря на то что новый дизайн получился бесполезным, мы все еще можем наблюдать рост процента экономии при проведении нашего эксперимента.
Как такое могло произойти? Это может произойти из-за того, что мы используем выборку. Приведу пример: если я случайном образом выберу 100 людей из десяти тысячной толпы и вычислю их средний рост, результат составит, например, 170 см. Но проведя данный эксперимент еще несколько раз, результат будет 177 см, 168 см и так далее.
Так как мы вычисляем статистику используя выборки, а не всё целое, средние значения каждой выборки будут различаться.
Зная, что использование выборок приводит к вариациям, мы можем переформулировать предыдущий вопрос:
В случае если новый дизайн на самом деле никак не влияет на экономию пользователей, какова вероятность того, что мы обнаружим настолько же высокий рост экономии, как и при случайном стечении обстоятельств?
Формально говоря, мы формулируем нулевую гипотезу следующим образом: рост процента экономии контрольной группы равен росту процента экономии экспериментальной группы.
Теперь наша работа заключается в проверке данной нулевой гипотезы. Мы можем сделать это проведя мысленный эксперимент.
Представьте, что мы можем проводить наш эксперимент снова и снова. При этом, мы все еще рассматриваем ситуацию, в которой новый дизайн никак не влияет на экономию пользователей. Что мы будем наблюдать?
Для тех, кому интересно, вот как мы это представляем:
Для каждой группы генерируем 500 нормально распределенных случайных величин с такими же статистическими характеристиками, как и у контрольной группы (среднее значение = 12%, среднеквадратическое отклонение = 5%). Теперь у нас есть контрольная группа и экспериментальная группа (средние значения одинаковы, так как мы рассматриваем ситуацию, в которой новый дизайн не имеет никакого эффекта). Технически, правильнее было бы использовать распределение Пуассона, но мы используем нормальное распределение для простоты примера.
В итоге, мы получаем гистограмму, приведенную ниже. Данная гистограмма показывает, насколько сильно среднее значение процента экономии между группами различается из-за случайного стечения обстоятельств (обусловленное использованием выборки).
Красная вертикальная линия показывает тот результат, который получил наш клиент при проведении эксперимента (1%). Для нас важен процент количества значений справа от красной линии — он показывает вероятность того, что при проведении эксперимента мы получим разность, равную 1% или выше (мы используем односторонний критерий, потому что он легче для понимания).
В данном случае это значение очень маленькое — из 10 000 экспериментов только в 9 мы получили разность процентов экономии групп, равную 1% или выше.
Это означает, что результат, который наш клиент получил при проведении эксперимента, по случайному стечению обстоятельств может быть получен с вероятностью лишь 0.09%!
Данная вероятность, 0.09%, является нашим p-значением. «Каким значением? Хватит забрасывать меня какими-то случайными терминами!» — вы можете подумать. И правда, когда дело доходит до проверки статистических гипотез, приходится использовать много различных терминов, и, мы, пожалуй, оставим их разъяснение Википедии.
Наша задача, как и всегда, состоит в построении интуитивного понимания того, как работают эти инструменты статистики и для чего они пользуются, поэтому по возможности мы постараемся избегать использования терминологии в пользу простоты объяснении. Однако, p-значение является крайне необходимым термином, с которым вы еще не раз встретитесь в мире науки о данных, поэтому его мы должны обсудить. P-значение (в нашем случае 0.09%) представляет собой:
Вероятность получения, наблюдаемого нами результата, в случае если нулевая гипотеза правильна.
Соответственно, мы можем использовать p-значение для проверки справедливости нулевой гипотеза. Основываясь на определении, кажется, что мы хотим, чтобы это значение было минимальным, так как, чем меньше p-значение, тем менее вероятно то, что результат нашего эксперимента был случайным. Но на практике, мы введем уровень значимости для p-значения (называемый «альфа»), и, в случае если p-значение меньше альфа, мы отвергаем нулевую гипотезу и делаем вывод, что полученный результат и эффект реальны (статистически значимы).
Теперь давайте рассмотрим способ быстрого вычисления p-значения.
Время поговорить об одной из фундаментальных концепций статистики. Центральная предельная теорема утверждает, что при сложении независимых случайных величин, их сумма стремится к нормальному распределению по мере сложения всё большего количества величин. Центральная предельная теорема работает даже в случае, если случайные величины не имеют нормального распределения.
Другими словами, если мы вычислим средние значения набора выборок (подразумевая, что все наши наблюдения независимы друг от друга, как, например, друг от друга не зависят броски монетки), распределение всех этих выборок будет близко к нормальному.
Взгляните на гистограмму, которую мы построили ранее. Выглядит как нормальное распределение, не так ли? Мы можем проверить нормальность с помощью КК (квантиль-квантиль) графика, который сравнивает квантиль нашего распределения с другим квантилем (в нашем случае, с нормальным распределением). Если наше распределение нормальное, то КК график будет близок к красной линии, находящейся под углом в 45°. И именно так и получается, здорово!
Значит, когда мы проводили наш эксперимент снова и снова, это был пример работы центральной предельной теоремы!
Так почему же это так важно?
Помните, как мы проверяли нашу нулевую гипотезу, проводя 10 000 экспериментов? Звучит очень утомительно, не так ли? На практике, это и утомительно, и дорого. Но благодаря центральной предельной теореме мы можем это избежать!
Теперь мы знаем, что распределение наших повторяющихся экспериментов будет нормальным, и мы можем использовать это знание для определения того, как распределяться наши 10 000 экспериментов без их проведения!
Здорово! Теперь у нас есть всё, что нам требуется для проверки гипотезы. Давайте завершим работу для нашего клиента.
Среднеквадратическое отклонение равно 5% как для контрольной группы, так и для экспериментальной группы, поэтому наша выборочная дисперсия равна 0.0025. N — это количество наблюдений в каждой группе, поэтому N равно 500. Подставляем числа в формулу и получаем стандартную ошибку, равную 0.316%.
from scipy.stats import norm
P-значение (0.0016) меньше альфа (0.05), поэтому мы отвергаем нулевую гипотезу и говорим клиенту, что новый дизайн на самом деле помогает пользователям лучше экономить. Ура, победа!
Но обратите еще внимание на то, что p-значение, которое мы вычислили аналитически (0.0016), отличается от значения 0.0009, которое мы получили ранее. Связано это с тем, что наша симуляция была односторонней (односторонний тест более легок для понимания и визуализации). Мы можем удвоить данное значение для получения 0.0018, примерно равного настоящему 0.0016.
В реальной жизни A/B тестирование не настолько легко как в нашем выдуманном примере. Скорее всего, наш клиент не будет обладать готовыми данными, и нам придется самим искать нужные данные. Приведу несколько трудных моментов, с которыми вы можете встретиться при A/B тестировании:
Надеюсь, данная статья была для вас полезна!
12. Проверка статистических гипотез
Продолжаем проверять статистические гипотезы – всё новые и новые, новые и новые, до полного насыщения! Исправляя оплошность (запамятовал), хочу порекомендовать эту увлекательную тему в качестве основного или дополнительного материала для вашего научного проекта (курсовика, диплома, диссертации) или прикладного исследования. Причём, самому широкому кругу читателей, в том числе экономистам, социологам, психологам – всем, кто работает со статистическими данными. Здесь и научная новизна, и практическая значимость, и широкий простор для творчества! И несложные вычисления, что немаловажно.
Как вы знаете (а если нет, то ссылка выше), все статистические гипотезы делятся на два вида:
I) Гипотеза о законе распределения статистической совокупности. Этому виду гипотез посвящен следующий урок – Критерий согласия Пирсона.
II) Вторая большая группа гипотез касается числовых характеристик стат. совокупностей, закон распределения которых уже известен:
Существуют и другие статистические гипотезы, с которыми можно ознакомиться, например, в учебном пособии В. Е. Гмурмана (поздние издания). Кроме того, в рамках сайта я рассмотрю статистическую гипотезу о значимости коэффициента корреляции и не только – со временем добавлю их в этот список.
Вникаем, решаем и получаем удовольствие!
Гипотеза о равенстве генеральных средних двух распределений
Постановка задачи: из двух генеральных совокупностей извлечены выборки объёмов 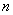
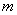
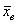
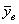

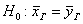
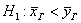
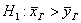
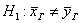
При этом возможны следующие вариации задачи:
а) выборки независимы, генеральные совокупности распределены нормально и известны их дисперсии  .
.
Тогда для проверки нулевой гипотезы используют статистический критерий 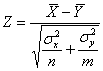
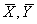
Критическая область однозначно определяется критическим значением 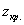
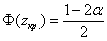
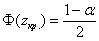
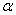
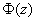
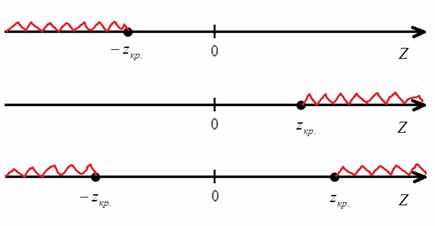
Далее на основании выборочных данных рассчитывается наблюдаемое значение критерия:
Если 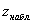
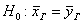
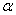
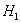
По выборке объема 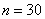
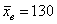
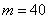
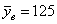
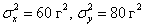
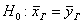
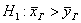
. я, конечно, не знаю, у каких современных станков могут быть такие конские дисперсии, тут, скорее, речь о двух бабулях, которые пекут одинаковые пирожки дедовским методом 🙂 И нужно выяснить, одинаковый ли у них выхлоп или первая бабушка более щедрая.
Решаем: по условию, известны генеральные дисперсии, поэтому для проверки гипотезы о равенстве генеральных средних используем критерий 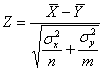
Для конкурирующей гипотезы 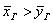

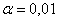
По таблице значений функции Лапласа или с помощью Калькулятора (Пункт 5*) определяем, что этому значению функции соответствует аргумент 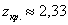
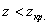
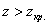

На чистовике эти чертежи выполнять не обязательно – они нужны, чтобы вы лучше видели ситуацию.
По выборочным данным вычислим наблюдаемое значение критерия:
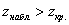
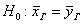
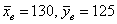
Но это ещё не значит, что нужно покупать пирожки у «иксовой» бабули, они ведь могут оказаться менее вкусными 🙂
Ответ: на уровне значимости 0,01 нулевую гипотезу отвергаем.
И еще раз повторим, что это значит. Это значит, что с вероятностью 1% мы совершили ошибку первого рода (отвергли правильную гипотезу).
Следующая задача для самостоятельного решения:
Из продукции двух автоматических линий извлечены по 50 гвоздей и вычислены их выборочные средние длины 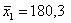
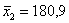
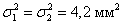
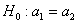
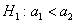
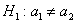
Краткое решение и ответ в конце урока, особую аккуратность проявите в обозначениях – в аналогичных задачах они бывают разными.
Та же гипотеза, другая ситуация:
б) независимые выборки достаточно большие  , генеральные дисперсии неизвестны, причём ген. совокупности могут иметь и другое распределение (не нормальное)
, генеральные дисперсии неизвестны, причём ген. совокупности могут иметь и другое распределение (не нормальное)
Условие 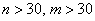
В этом случае можно использовать похожий, но приближенный критерий 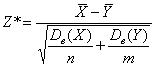
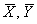
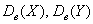
Исправлением дисперсий тут можно пренебречь (т.к. выборки большие), но лично я бы исправил. Впрочем, результаты такой проверки всё равно будут менее «авторитетными».
Ситуация более тяжелая:
в) это малые независимые выборки  , ген. совокупности распределены нормально и дисперсии их не известны
, ген. совокупности распределены нормально и дисперсии их не известны
В этом случае выборочные дисперсии дают плохую оценку генеральных дисперсий, поэтому критерий предыдущего пункта не годится. Но если предположить или доказать, что генеральные дисперсии одинаковы (хотя и не известны), то для проверки гипотезы 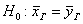
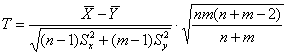
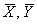
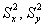
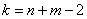
Из двух партий деталей, изготовленных одинаковыми станками, извлечены выборки объемами 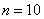
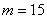
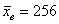
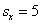
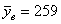
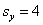
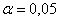
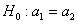
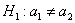
В этом тяжелом случае нам удалось раздобыть всего лишь 10 и 15 гвоздей, но ситуацию спасает то, что станки одинаковые, поэтому можно смело допустить, что их погрешности (ген. дисперсии) одинаковы. Кроме того, можно проверить гипотезу о равенстве генеральных дисперсий, до которой мы ещё доберёмся.
Решение: полагая, что генеральные дисперсии одинаковы, используем критерий 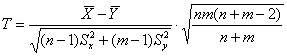
Поскольку конкурирующая гипотеза имеет вид 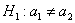
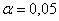
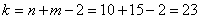
При 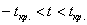
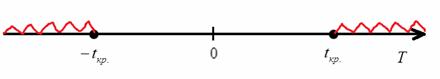
Вычислим наблюдаемое значение критерия: 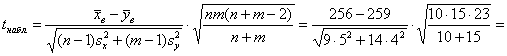
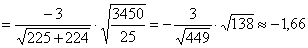
Таким различие выборочных средних 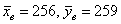
Ответ: на уровне значимости 0,05 гипотезу 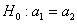
Задача для самостоятельного решения будет в параграфе Гипотеза о равенстве двух генеральных дисперсий, поскольку для того, чтобы пользоваться равенством ген. дисперсий, строго говоря и по меньшей мере, его нужно ещё проверить статистически.
И ещё один случай:
г) ген. совокупности распределены нормально, ген. дисперсии неизвестны, выборки зависимы
Здесь рассматриваются выборки одинакового объёма, варианты которых попарно зависимы. Что это значит? Пример: возьмём 50 помидоров и измерим их диаметр линейкой: 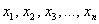
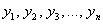
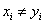
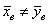
В случае зависимых выборок гипотеза о равенстве генеральных средних сводится к уже разобранной гипотезе о значении генеральной средней. Представим, что описанные выше попарные опыты проводятся много-много раз. Тогда речь заходит о случайной величине 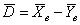
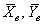
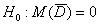
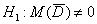
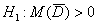
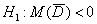
Технику решения рассмотрим на конкретном примере, социологическая задача, и никаких гвоздей:
Физическая подготовка 9 спортсменов была проведена при поступлении в спортивную школу, а затем после недели тренировок. Итоги проверки в баллах оказались следующими: 
(в 1-й строке число баллов при поступлении, во 2-й – после недели тренировок)
Требуется на уровне значимости 0,05 установить, значимо или незначимо улучшилась физическая подготовка спортсменов, в предположении, что число баллов распределено нормально.
И предположение это небезосновательно, т. к. человеческие характеристики, как правило, распределены нормально.
Решение: проверим гипотезу о том, что матожидание случайной величины 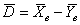
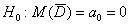
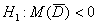
Так как генеральная дисперсия этой случайной величины не известна, то используем знакомый критерий 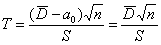
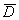
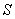
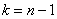
Для уровня значимости 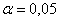

При 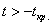
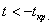
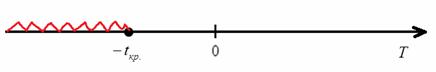
Для нахождения наблюдаемого значения критерия 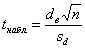
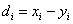
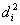
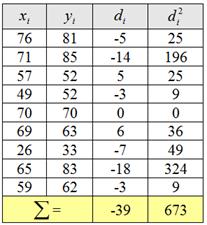
Вычислим выборочную среднюю разницу:
Вычислим исправленное стандартное отклонение, не сторонник я «ускоренных» формул, но здесь она удобна:
Таким образом: 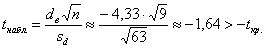
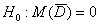
В данном случае это более удачная формулировка, нежели «гипотезу принимаем».
Таким образом, средняя разница 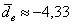
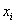
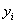
Ответ: на уровне значимости 0,05 нет оснований утверждать, что после недельной тренировки физическая форма спортсменов значимо улучшилась.
Продолжаем тему самостоятельно:
Две химические лаборатории исследовали 8 проб на допинг одним и тем же методом. Получены следующие результаты (процент содержания некоторого вещества в соответствующих пробах):
Требуется на уровне значимости 0,05 определить, значимо или незначимо различаются средние результаты анализов, в предположении, что они распределены нормально.
Иными словами, определите, не занесли ли в какую-нибудь лабораторию деньги 🙂
Как обычно, все числа уже в Экселе; продублирую также ссылки на таблицу критических точек распределению Стьюдента и Калькулятор (Пункт 10в).
С другими гипотезами всё проще:
Гипотеза о генеральной дисперсии нормального распределения
Она по своей сути похожа на гипотезу о генеральной средней: есть основания полагать, что генеральная дисперсия 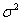
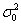
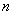
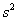
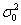
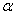
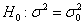
Для проверки этой гипотезы использует критерий 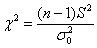
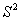
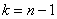
Критическая область зависит от вида конкурирующей гипотезы, а критические значения можно определить по соответствующей таблице либо с помощью Калькулятора (Пункт 11б).
1) Для гипотезы 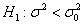
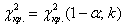

2) Для гипотезы 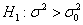
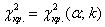

3) И для гипотезы 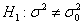
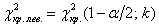
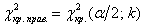

Если наблюдаемое значение критерия 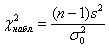
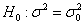
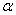
Классическая задача по теме – это задача о точности какого-нибудь прибора, станка или метода измерения:
Допустимая погрешность измерительного прибора по паспорту составляет 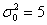
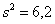
Или, попросту говоря, не лажает ли этот прибор.
Решение: полагая, что погрешность измерений распределена нормально, проверим гипотезу о том, что генеральная дисперсия действительно равна 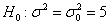
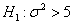
Используем критерий 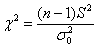
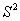
Найдём правостороннюю критическую область. Для уровня значимости 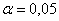
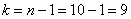
При 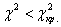
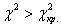

Вычислим наблюдаемое значение критерия: 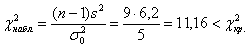

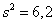
Возможно, у вас сложилось впечатление, что значения 5 и 6,2 различаются существенно, но это иллюзия – ведь дисперсия имеет квадратичную размерность, и стандартные отклонения действительно довольно близкИ друг к другу: 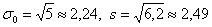
Ответ: на уровне значимости 0,05 точность прибора соответствует норме.
Партия изделий принимается, если дисперсия контролируемого размера значимо не превышает 0,2. Исправленная выборочная дисперсия, найденная по выборке объема 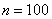
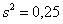
Таблица здесь не годится, поэтому пользуемся Калькулятором (Пункт 11б). За неимением Экселя используйте приближенную формулу Уилсона-Гильферти: 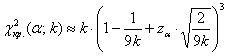
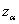
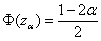
Сейчас для интереса проверил – погрешность составила всего одну сотую!
Гипотеза о равенстве генеральных дисперсий двух нормальных распределений
Две средние мы уже сравнивали, очередь за дисперсиями. Из двух нормальных ген. совокупностей извлечены независимые выборки объёмом 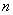
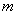
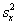
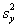
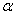
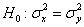
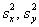
Для проверки этой гипотезы используют критерий 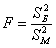
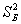
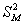
Данная случайная величина имеет распределение Фишера-Снедекора (так называемое F-распределение) со степенями свободы 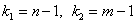
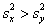
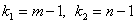
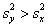
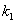
В качестве альтернативы рассматривают одну из следующих гипотез:
1) 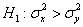
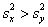
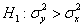
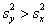

Критическое значение 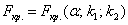
2) 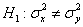

Однако для решения нашей задачи достаточно найти лишь правое критическое значение 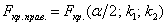
Дело в том, что 
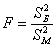
Далее на основании выборочных данных рассчитывается наблюдаемое значение критерия 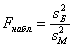
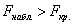
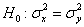
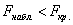
Рассматриваемая гипотеза часто возникает, когда требуется сравнить точность двух приборов, инструментов, станков, двух методов исследования. И сейчас мы разберём эту стандартную задачу:
Некоторая физическая величина измерена 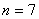
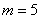
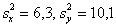
Ситуации тут могут быть разные: это измерение двумя однотипными инструментами (например, двумя линейками), или инструментами разными (например, линейкой и штангенциркулем), или речь вообще идёт о двух методах измерения (например, с зажмуренным левым и правым глазом).
И возникает вопрос: различие между 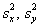
Решение: полагая, что погрешности измерений распределены нормально, проверим гипотезу 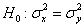
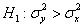
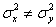
Для проверки гипотезы используем критерий 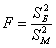
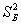
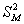
Найдём критическое значение 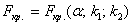
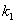
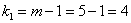
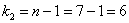
При 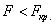
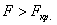
Вычислим наблюдаемое значение критерия: 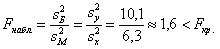
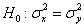
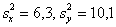
Так, если бы было проведено в 10 раз больше измерений 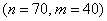
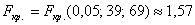
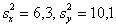
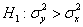
Ответ: на уровне значимости 0,05 точность способов измерения одинакова.
Творческая задача для самостоятельного решения, случай из жизни:
Две группы студентов-первокурсников написали контрольную по математическому анализу со следующими результатами: 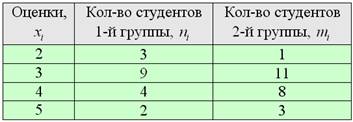
Предполагая, что успеваемость студентов распределена нормально, на уровне значимости 0,1:
1) Проверить гипотезу 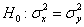
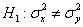
и в случае однородности групп обещанный пунктик:
2) Проверить гипотезу 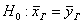
Вспоминаем, что такое дискретный вариационный ряд и как рассчитываются его характеристики. Не позволяй душе лениться! – в жизни пригодится, все числа уже в Экселе.
Ну что, порешаем ещё задачки? …конечно, порешаем! – ведь я маньяк в лучшем смысле этого слова:
Гипотеза о вероятности события
Пусть в достаточно большом количестве 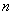
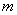
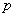
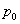
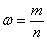
Для проверки гипотезы 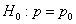
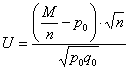
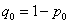
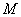

Далее технически всё похоже на гипотезу о генеральной средней. Для конкурирующей гипотезы 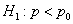
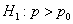
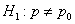
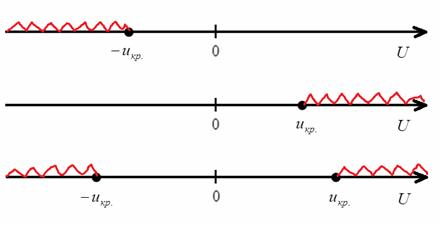
Критическое значение отыскивается из соотношения 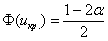
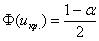
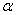
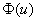
Если наблюдаемое значение критерия 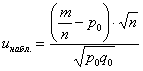
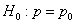
В результате длительных наблюдений установлено, что вероятность полного выздоровления больного, принимавшего лекарство 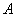
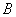
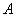
Итак, в результате использования нового лекарство получена относительная частота полного выздоровления 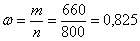
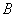
Решение: на уровне значимости 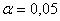
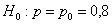
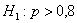
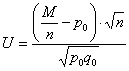
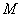
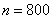
Критическое значение правосторонней критической области найдём из соотношения 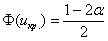
По таблице значений функции Лапласа или с помощью Калькулятора (Пункт 5*), определяем, что этому значению функции соответствует аргумент 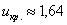
При 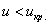
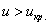
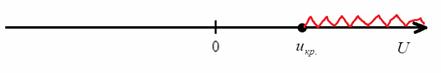
Вычислим 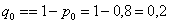
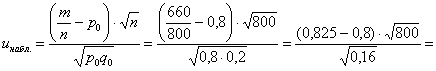
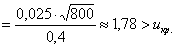
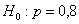
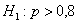
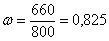
Ответ: на пятипроцентном уровне значимости новое лекарство эффективнее лекарства 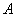
Завод рассылает рекламные каталоги возможным заказчикам. Как показал опыт, вероятность того, что организация, получившая каталог, закажет рекламируемое изделие, равна 0,08. Завод разослал 1000 каталогов новой улучшенной формы и получил 98 заказов. Можно ли считать, что новая форма рекламы значимо эффективнее?
Примите уровень значимости 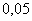
И заключительный параграф этой интереснейшей статьи:
Сравнение вероятностей двух биномиальных распределений
На самом деле о вероятности биномиального распределения речь уже шла в предыдущей гипотезе, и теперь перед нами стоит задача сравнить вероятности двух биномиальных распределений.
Пусть в двух генеральных совокупностях проводятся независимые испытания, в каждом из которых событие 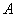
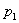
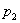
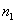
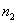
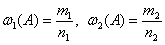
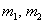
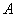
Требуется оценить, значимо или незначимо отличаются друг от друга относительные частоты. Незначимое отличие объяснимо случайными факторами и справедливостью гипотезы 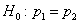
Для проверки этой гипотезы используют критерий: 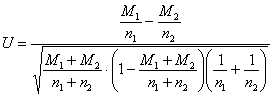
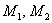
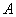
В качестве альтернативы рассматривают гипотезу 
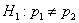
Возвращаемся к нашим помидорам:
От двух поставщиков в магазин поступило 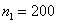
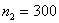
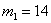
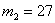
Очевидно, что здесь существуют вполне конкретные вероятности 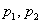
И возникает вопрос: эта разница случайна или нет?
Решение: на уровне значимости 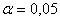
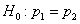
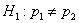
Критическое значение двусторонней критической области найдём из соотношения 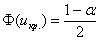
По таблице значений функции Лапласа или с помощью Калькулятора (Пункт 5*) определяем 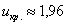
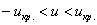
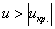

Вычислим наблюдаемое значение критерия: 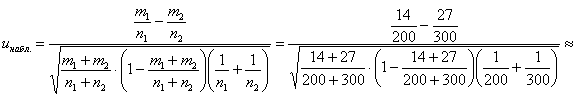
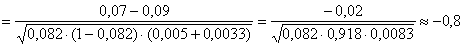
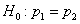
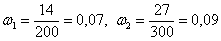
Ответ: на уровне значимости 0,05 нет оснований отдавать предпочтение какому-то одному из поставщиков
Как говорится, что там помидоры, что там.
И почётное право завершить этот урок предоставляется героям, которые помогали нам на протяжении всего курса тервера, ну а может и некоторые читатели уже взялись за оружие:))
Два стрелка совершили по 50 выстрелов в цель. Первый стрелок поразил цель 41 раз, а второй – 36. Можно ли на уровне значимости 0,1 утверждать, что первый стрелок более меткий?
Решение и ответ совсем близко.
Но и это ещё не всё! На очереди важнейшая и очень распространённая гипотеза о законе распределения генеральной совокупности.
Пример 41. Решение: по условию, известны генеральные дисперсии, поэтому для проверки гипотезы используем критерий 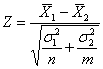
а) Для гипотезы 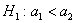
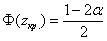
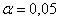
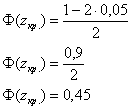
По таблице значений функции Лапласа определяем 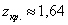
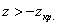
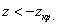
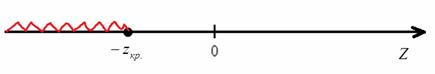
Вычислим наблюдаемое значение критерия:
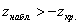
б) Для гипотезы 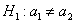

Критическое значение найдём из соотношения 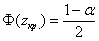
Наблюдаемое значение критерия 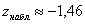
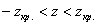
Ответ: в обоих случаях гипотезу 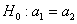
Напоминаю, что это не 100%-ное доказательство гипотезы, т.к. существует 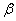
Пример 44. Решение: рассмотрим случайную величину 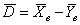
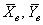
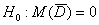
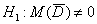
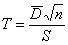
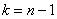
Для уровня значимости 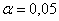
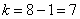
Таким образом, при 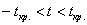
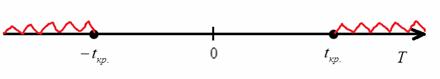
Найдём наблюдаемое значение критерия. Для этого нужно вычислить выборочную среднюю разницу 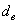
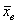
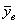
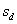
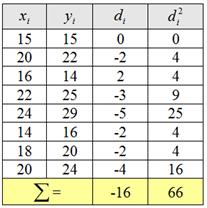
Таким образом:
Наблюдаемое значение критерия:
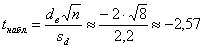
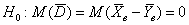
Ответ: на уровне значимости 0,05 результаты лабораторий отличны друг от друга.
Пример 46. Решение: полагая, что погрешности размера выпускаемых изделий распределены нормально, проверим гипотезу 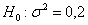
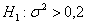
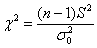
Так как в конкурирующей гипотезе речь идёт о бОльших значениях дисперсии, то критическая область будет правосторонней. Найдём критическое значение. Для уровня значимости 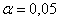
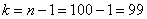
При 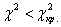
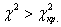
Вычислим наблюдаемое значение критерия: 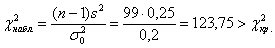
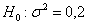
Иными словами, выборочный результат 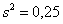
Ответ: на уровне значимости 0,05 партию изделий принять нельзя.
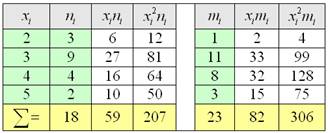
Пример 48. Решение: Заполним расчётную таблицу:
Вычислим выборочные характеристики. Средний балл: 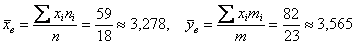
Выборочные дисперсии: 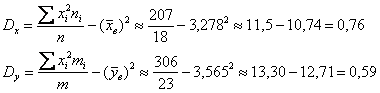
Исправленные дисперсии:
1) На уровне значимости 0,1 проверим гипотезу 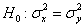
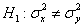
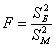
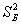
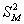
Найдём правое критическое значение двусторонней критической области. Для уровня значимости 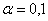
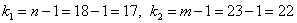
Вычислим наблюдаемое значение критерия: 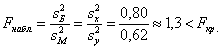
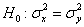
Замечание: здесь, конечно, речь идёт не о строгом, а о примерном равенстве генеральных дисперсий.
2) На уровне значимости 0,1 проверим гипотезу 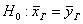
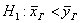
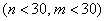
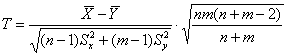
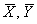
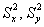
При 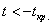
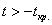
Вычислим наблюдаемое значение критерия: 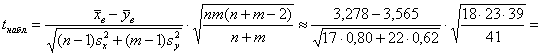

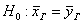
Таким образом, по результатам контрольной работы нельзя утверждать, что различие между средними оценками 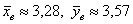
Ответ: на уровне значимости 0,1 нет оснований отвергнуть нулевые гипотезы.
Пример 50. Решение: на уровне значимости 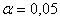
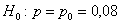
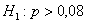
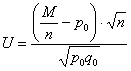
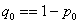
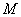
Найдём критическое значение правосторонней критической области: 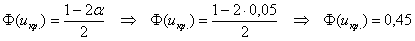
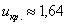
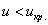
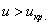
Вычислим наблюдаемое значение критерия: 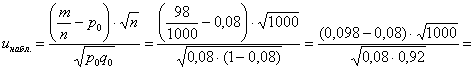
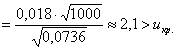
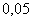
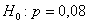
Ответ: на уровне значимости 0,05 новая форма рекламы значимо эффективнее.
Пример 52. Решение: на уровне значимости 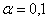
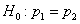
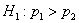
Найдём критическое значение правосторонней критической области: 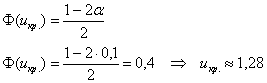
При 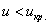
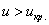
Вычислим наблюдаемое значение критерия: 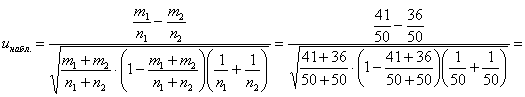
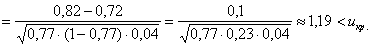
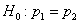
Ответ: на уровне значимости 0,1 нет оснований считать, что 1-й стрелок более меткий.
Автор: Емелин Александр
(Переход на главную страницу)


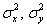 .
.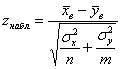
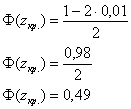
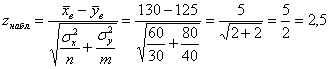
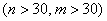 , генеральные дисперсии неизвестны, причём ген. совокупности могут иметь и другое распределение (не нормальное)
, генеральные дисперсии неизвестны, причём ген. совокупности могут иметь и другое распределение (не нормальное)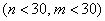 , ген. совокупности распределены нормально и дисперсии их не известны
, ген. совокупности распределены нормально и дисперсии их не известны