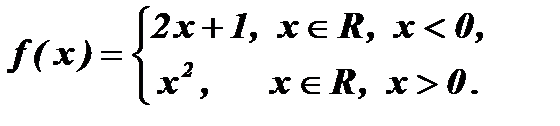Что нужно указать чтобы функция считалась заданной
Функция. Способы задания функций.
Функция является заданной, иначе говоря, известной, если для каждого значения возможного числа аргументов можно узнать соответствующее значение функции. Наиболее распространенные три способа задания функции: табличный, графический, аналитический, существуют еще словесный и рекурсивный способы.
1. Табличный способ наиболее широко распространен (таблицы логарифмов, квадратных корней), основное его достоинство – возможность получения числового значения функции, недостатки заключаются в том, что таблица может быть трудно читаема и иногда не содержит промежуточных значений аргумента.
Аргумент х принимает заданные в таблице значения, а у определяется соответственно этому аргументу х.
2. Графический способ заключается в проведении линии (графика), у которой абсциссы изображают значения аргумента, а ординаты – соответствующие значения функции. Часто для наглядности масштабы на осях принимают разными.
Например: для нахождения по графику у, которому соответствует х = 2,5 необходимо провести перпендикуляр к оси х на отметке 2,5. Отметку можно довольно точно сделать с помощью линейки. Тогда найдем, что при х = 2,5 у равно 7,5, однако если нам необходимо найти значение у при х равном 2,76, то графический способ задания функции не будет достаточно точным, т.к. линейка не дает возможности для столь точного замера.
Достоинства этого способа задания функций заключаются в легкости и целостности восприятия, в непрерывности изменения аргумента; недостатком является уменьшение степени точности и сложность получения точных значений.
3. Аналитический способ состоит в задании функции одной или несколькими формулами. Основным достоинством этого способа является высокая точность определения функции от интересующего аргумента, а недостатком является затрата времени на проведение дополнительных математических операций.
4. Словесный способ состоит в задании функции обычным языком, т.е. словами. При этом необходимо дать входные, выходные значения и соответствие между ними.
Словесно можно задать функцию (задачу), принимающуюся в виде натурального аргумента х с соответствующим значением суммы цифр, из которых состоит значение у. Поясняем: если х равно 4, то у равно 4, а если х равно 358, то у равен сумме 3 + 5 + 8, т. е 16. Далее аналогично.
5. Рекурсивный способ состоит в задании функции через саму себя, при этом значения функции определяются через другие ее же значения. Такой способ задания функции используется в задании множеств и рядов.
При разложении числа Эйлера задается функцией:
Ее сокращение приведено ниже:
При прямом расчёте возникает бесконечная рекурсия, но можно доказать, что значение f(n) при возрастании n стремится к единице (поэтому, несмотря на бесконечность ряда, значение числа Эйлера конечно). Для приближённого вычисления значения e достаточно искусственно ограничить глубину рекурсии некоторым наперёд заданным числом и по достижении его использовать вместо f(n) единицу.
Как решать задачи на функцию
Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок «Что такое функция в математике».
После того, как вы действительно поймете, что такое функция (возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.
В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.
Как получить значение функции
Рассмотрим задание. Функция задана формулой « y = 2x − 1 »
Для того, чтобы вычислить « y » при « x = 15 » достаточно подставить в функцию вместо « x » необходимое числовое значение.
Запись решения выглядит следующим образом.
Для того, чтобы найти « x » по известному « y », необходимо подставить вместо « y » в формулу функции числовое значение.
Мы получили линейное уравнение с неизвестным « x », которое решается по правилам решения линейных уравнений.
Не забывайте про правило переноса в уравнениях.
Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас требуется умножить и левую, и правую часть на « −1 » для смены знака.
Как проверить верно ли равенство для функции
Рассмотрим задание. Функция задана формулой « f(x) = 2 − 5x ».
Верно ли равенство « f(−2) = −18 »?
Чтобы проверить верно ли равенство, нужно подставить в функцию « f(x) = 2 − 5x » числовое значение « x = −2 » и сопоставить с тем, что получится при расчетах.
Когда подставляете отрицательное число вместо « x », обязательно заключайте его в скобки.
Не забывайте использовать правило знаков.
Неправильно
Правильно
С помощью расчетов мы получили « f(−2) = 12 ».
Это означает, что « f(−2) = −18 » для функции « f(x) = 2 − 5x » не является верным равенством.
Как проверить, что точка принадлежит графику функции
Рассмотрим функцию « y = x 2 −5x + 6 »
Для этой задачи нет необходимости, строить график заданной функции.
Чтобы определить, принадлежит ли точка функции, достаточно подставить её координаты в функцию (координату по оси « Ox » вместо « x » и координату по оси « Oy » вместо « y »).
Вместо « x » подставим « 1 ». Вместо « y » подставим « 2 ».
У нас получилось верное равенство, значит, точка с координатами (1; 2) принадлежит заданной функции.
Вместо « x » подставим « 0 ». Вместо « y » подставим « 1 ».
В этом случае мы не получили верное равенство. Это означает, что точка с координатами (0; 1) не принадлежит функции « y = x 2 − 5x + 6 »
Как получить координаты точки функции
С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат в формулу функции получается верное равенство.
Рассмотрим функцию « y(x) = −2x + 1 ». Её график мы уже строили в предыдущем уроке.
Для этого из значения « 2 » на оси « Ox » проведем перпендикуляр к графику функции. Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси « Oy ».
Полученное значение « −3 » на оси « Oy » и будет искомым значением « y ».
Убедимся, что мы правильно сняли координаты точки для x = 2
в функции « y(x) = −2x + 1 ».
Значит, мы правильно получили координаты с графика функции.
Все полученные координаты точки с графика функции обязательно проверяйте подстановкой значений « x » в функцию.
При подстановке числового значения « x » в функцию в результате должно получиться то же значение « y », которое вы получили на графике.
При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».
Только подстановка значений в формулу функции дает точные результаты.
Способы задания функции
Замечание: Функция считается заданной, если известна область определения функции и указано правило, по которому для каждого значения аргумента из области определения можно найти соответствующее значение функции.
1. Табличный способ: значения аргумента и соответствующие значения функции записаны в виде таблицы.
Достоинства: простой способ.
Недостатки: не дает полного представления о функции; не является наглядным.
Замечание: В результате экспериментального изучения какого-нибудь явления или процесса (испытание самолетов, моторов, урожайности семян) всегда устанавливается функциональная зависимость между переменными в виде таблицы.
2. Графический способ:функция задана с помощью графика.
Определение: Графиком функции называется множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Достоинства: наглядный способ.
Недостатки: небольшая точность при определении значений функции при данных значениях аргумента; ограниченность промежутка, на котором может быть построен график функции.
Замечание: Иногда табличный и графический способы задания функции являются единственно возможными, в других случаях используются как дополнительные. Метеорологи составляют таблицы выпавших осадков.В медицине о работе сердца судят по кардиограмме, которую создает прибор – кардиограф; вибратор регистрирует колебания различных сооружений (мостов, судов, зданий).
3. Аналитический способ:функция задана с помощью формулы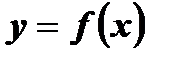 
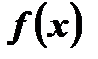
, где
–выражение с переменной х.
Достоинства: значения функции могут быть вычислены для любого значения аргумента из области определения функции.
Недостатки: не является наглядным.
Замечание:
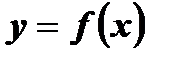
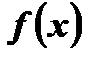
1. Для аналитически заданной функции иногда не задают область определения явно. В таком случае область определения функции совпадает с областью определения выражения 
.
2. Одной и той же формулой можно задать различные функции, изменяя область определения.
3. Функция может быть задана различными формулами на различных промежутках области определения.
Пример:
1. Если функция задана формулой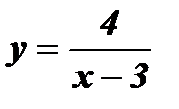 
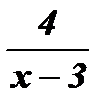
без указания области ее определения, то предполагается, что область определения этой функции – множество всех действительных чисел, кроме числа 3 (при х = 3 выражение 
не имеет смысла ).
3. 
4. 
. 
– целая часть числа х, то есть наибольшее целое число, не превосходящее х. 
; 
; 
; 
.
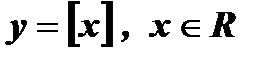
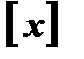
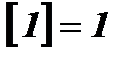
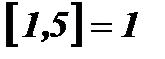
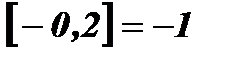
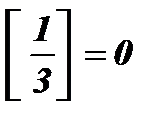
4. Словесное описание:если формулу, задающую функцию, записать сложно или невозможно, пользуются словесным описанием способа, задающего функцию.
Пример: Функция Дирихле:
, если х – рационально; 
, если х – иррационально.
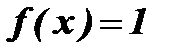
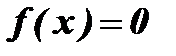
Упражнения:
а)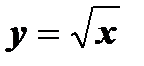 
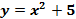
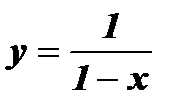
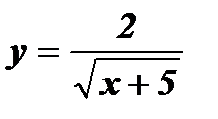
; б) 
; в) 
; г) 
;
д) 
; е) 
; ж) 
; з)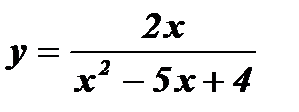 
.
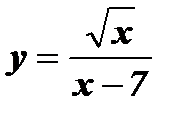
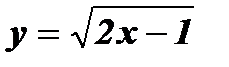
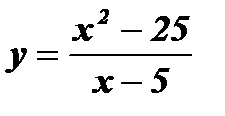
Дата добавления: 2016-11-02 ; просмотров: 1249 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Как решать задачи на функцию
Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок «Что такое функция в математике».
После того, как вы действительно поймете, что такое функция (возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.
В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.
Как получить значение функции
Рассмотрим задание. Функция задана формулой « y = 2x − 1 »
Для того, чтобы вычислить « y » при « x = 15 » достаточно подставить в функцию вместо « x » необходимое числовое значение.
Запись решения выглядит следующим образом.
Для того, чтобы найти « x » по известному « y », необходимо подставить вместо « y » в формулу функции числовое значение.
Мы получили линейное уравнение с неизвестным « x », которое решается по правилам решения линейных уравнений.
Не забывайте про правило переноса в уравнениях.
Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас требуется умножить и левую, и правую часть на « −1 » для смены знака.
Как проверить верно ли равенство для функции
Рассмотрим задание. Функция задана формулой « f(x) = 2 − 5x ».
Верно ли равенство « f(−2) = −18 »?
Чтобы проверить верно ли равенство, нужно подставить в функцию « f(x) = 2 − 5x » числовое значение « x = −2 » и сопоставить с тем, что получится при расчетах.
Когда подставляете отрицательное число вместо « x », обязательно заключайте его в скобки.
Не забывайте использовать правило знаков.
Неправильно
Правильно
С помощью расчетов мы получили « f(−2) = 12 ».
Это означает, что « f(−2) = −18 » для функции « f(x) = 2 − 5x » не является верным равенством.
Как проверить, что точка принадлежит графику функции
Рассмотрим функцию « y = x 2 −5x + 6 »
Для этой задачи нет необходимости, строить график заданной функции.
Чтобы определить, принадлежит ли точка функции, достаточно подставить её координаты в функцию (координату по оси « Ox » вместо « x » и координату по оси « Oy » вместо « y »).
Вместо « x » подставим « 1 ». Вместо « y » подставим « 2 ».
У нас получилось верное равенство, значит, точка с координатами (1; 2) принадлежит заданной функции.
Вместо « x » подставим « 0 ». Вместо « y » подставим « 1 ».
В этом случае мы не получили верное равенство. Это означает, что точка с координатами (0; 1) не принадлежит функции « y = x 2 − 5x + 6 »
Как получить координаты точки функции
С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат в формулу функции получается верное равенство.
Рассмотрим функцию « y(x) = −2x + 1 ». Её график мы уже строили в предыдущем уроке.
Для этого из значения « 2 » на оси « Ox » проведем перпендикуляр к графику функции. Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси « Oy ».
Полученное значение « −3 » на оси « Oy » и будет искомым значением « y ».
Убедимся, что мы правильно сняли координаты точки для x = 2
в функции « y(x) = −2x + 1 ».
Значит, мы правильно получили координаты с графика функции.
Все полученные координаты точки с графика функции обязательно проверяйте подстановкой значений « x » в функцию.
При подстановке числового значения « x » в функцию в результате должно получиться то же значение « y », которое вы получили на графике.
При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».
Только подстановка значений в формулу функции дает точные результаты.
Порядок действий в математике
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные операции в математике
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Подставляем полученные значения в исходное выражение:
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!