Что обозначает k в линейной функции
Как найти k и b по графику линейной функции?
В статье я расскажу про два простых способа найти \(k\) и \(b\), если известен график линейной функции.
Способ 1
Первый способ основывается на трех фактах:
Линейная функция пересекает ось \(y\) в точке \(b\).
Примеры:
Но не советую определять так \(b\), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.
Если функция возрастает, то знак коэффициента \(k\) плюс, если убывает – минус, а если постоянна, то \(k=0\).
Чтоб конкретнее определить \(k\) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить \(k\) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.

Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.
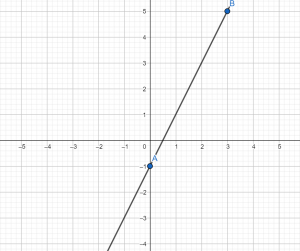
\(b=3\) – это сразу видно. Функция идет вниз, значит \(k 0\). \(k=+\frac
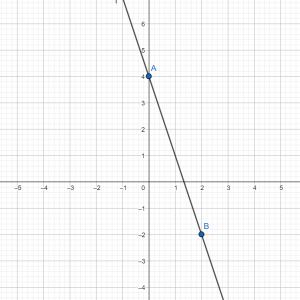
Теперь перейдем к функции \(g(x)\). Найдем координаты точек \(D\) и \(E\): \(D(-2;4)\), \(E(-4;1)\). Можно составить систему:
Вычтем второе уравнение из первого, чтоб убрать \(b\):
\(g(x)=1,5x+7\). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем \(f(x)\) и \(g(x)\).
Картинку в хорошем качестве, можно скачать нажав на кнопку «скачать статью».
График линейной функции, его свойства и формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Линейная функция, ее свойства и график
теория по математике 📈 функции
Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.
Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.
Число k называется угловым коэффициентом прямой.
Свойства линейной функции
Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.
Пример №1
Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:
Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).
Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:
Вписываем в таблицу значения у:
Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5), проводим через эти две точки прямую.
Итак, по формуле мы видим, что угловой коэффициент — положительный, значит, график – возрастает, что мы и видим на нашем графике.
Пример №2.
Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).
Пример №3
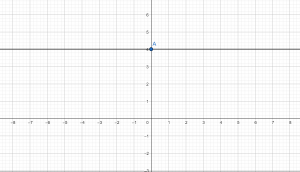
Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:
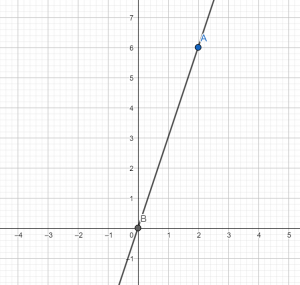
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ассмотрим коэффициенты под №3. Если k 90 0 ) угол с положит.направлением оси абсцисс (Ох). Если b 0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом ( 0 ). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b 0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
График данной функции зависит от k и b.
pазбирался: Даниил Романович | обсудить разбор | оценить
Линейная функция (ЕГЭ 2022)
Зависимость одной величины от другой математики называют функций одной величины от другой.
Количество денег — это функция вашей зарплаты (иногда говорят «от зарплаты»).
Вес — это функция от съеденных круассанов. Чем меньше съел, тем меньше весишь.
Расстояние — это функция времени. Чем дольше ты будешь идти, тем больше пройдешь.
Ну а теперь перейдем к одному из видов функций – линейной функции.
Линейная функция — коротко о главном
Линейная функция –это функция вида \( y=kx+b\), где \( k\) и \( b\) – любые числа (коэффициенты).
Рассмотрим, как коэффициенты влияют на месторасположение графика:
Общие варианты представлены на рисунке:
Линейная функция
Но сначала официальное определение «Функции» – теперь ты его поймешь. Держи в уме: деньги – зарплата, вес – круассаны, расстояние – время.
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).
Что значит «допустимому»?
Все дело в понятии «область определения»: для некоторых функций не все аргументы «одинаково полезны» — не все можно подставить в зависимость.
Например, для функции \( y=\sqrt
Ну и вернемся, наконец, к теме данной статьи.
Линейной называется функция вида \( y=kx+b\), где \( k\) и \( b\) – любые числа (они называются коэффициентами).
Другими словами, линейная функция – это такая зависимость, что функция прямо пропорциональна аргументу.
Как думаешь, почему она называется линейной?
Все просто: потому что графиком этой функции является прямая линия. Но об этом чуть позже.
Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения \( D\left( y \right)\) и область значений \( E\left( y \right)\).
Область определения линейной функции
Какими могут быть значения аргумента линейной функции \( y=kx+b\)? Правильно, любыми. Это значит, что область определения – все действительные числа:
\( D\left( y \right)=\mathbb
А множество значений?
Область значений линейной функции
Тут тоже все просто: поскольку функция прямо пропорциональна аргументу, то чем больше аргумент \( x\), тем больше значение функции \( y\).
Значит, \( y\) так же как и \( x\) может принимать все возможные значения, то есть \( E\left( y \right)=\mathbb
Верно, да не всегда. Есть такие линейные функции, которые не могут принимать любые значения. Как думаешь, в каком случае возникают ограничения?
Вспомним формулу: \( y=kx+b\). Какие нужно выбрать коэффициенты \( k\) и \( b\), чтобы значение функции y не зависело от аргумента \( x\)?
А вот какие: \( b\) – любое, но \( k=0\). И правда, каким бы ни был аргумент \( x\), при умножении на \( k=0\) получится \( 0\)!
Тогда функция станет равна \( y=0\cdot x+b=b\), то есть она принимает одно и то же значение при всех \( x\):
\( y = kx + b:<\rm< >>\left[ \begin
Теперь рассмотрим несколько задач на линейную функцию.
Три задачи на линейную функцию
Решение задачи №1
Пусть начальное значение аргумента равно некому числу \( <
Чему была равна функция до увеличения? Подставляем аргумент в формулу:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Решение задачи №2
Аналогично предыдущей задаче:
Начальное значение аргумента равно \( <
Начальное значение функции: \( <
В этот раз функция не увеличилась, а уменьшилась. Это значит, что конечное значение будет меньше начального, а значит, изменение (разность конечного и начального) будет отрицательным:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Определение прямой пропорциональной зависимости
Если проанализировать решения этих двух задач, можно прийти к важному выводу.
При изменении аргумента линейной функции на \( \Delta x\) функция изменяется на \( k\cdot \Delta x\). То есть изменение функции всегда ровно в \( \mathbf
\) раз больше изменения аргумента.
По сути это является определением прямой пропорциональной зависимости.
Решение задачи №3
Подставим известные значения аргумента и функции в формулу \( y=kx+b\):
Получили два уравнения относительно \( k\) и \( b\). Теперь достаточно решить систему этих двух уравнений:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
График линейной функции
Как я уже упоминал ранее, график такой функции – прямая линия.
Как известно из геометрии, прямую можно провести через две точки (то есть, если известны две точки, принадлежащие прямой, этого достаточно, чтобы ее начертить).
Предположим, у нас есть функция линейная функция \( y=2x+1\). Чтобы построить ее график, нужно вычислить координаты любых двух точек.
То есть нужно взять любые два значения аргумента \( x\) и вычислить соответствующие два значения функции.
Затем для каждой пары \( \left( x;y \right)\) найдем точку в системе координат, и проведем прямую через эти две точки.
Проще всего найти функцию, если аргумент \( x=0:y\left( 0 \right)=2\cdot 0+1=1\).
Итак, первая точка имеет координаты \( \left( 0;1 \right)\).
Теперь возьмем любое другое число в качестве \( x\), например, \( x=1:y\left( 1 \right)=2\cdot 1+1=3\).
Вторая точка имеет координаты \( \left( 1;3 \right)\).
Ставим эти две точки на координатной плоскости:
Теперь прикладываем линейку, и проводим прямую через эти две точки:
Вот и все, график построен!
Давай теперь на этом же рисунке построим еще два графика: \( y=
Построй их самостоятельно так же: посчитай значение y для любых двух значений \( x\), отметь эти точки на рисунке и проведи через них прямую.
Должно получиться так:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Видно, что все три прямые по-разному наклонены и в разных точках пересекают координатные оси. Все дело тут в коэффициентах \( \displaystyle k\) и \( \displaystyle b\).
Давай разберемся, на что они влияют.
Коэффициенты линейной функции
Для начала выясним, что делает коэффициент \( \displaystyle b\). Рассмотрим функцию \( \displaystyle y=x+b\), то есть \( \displaystyle k=1\).
Меняя \( \displaystyle b\) будем следить, что происходит с графиком.
Что ты можешь сказать о них? Чем отличаются графики?
Это сразу видно: чем больше \( \displaystyle b\), тем выше располагается прямая.
Более того, заметь такую вещь: график пересекает ось \( \displaystyle \mathbf
И правда. Как найти точку пересечения графика с осью \( \displaystyle y\)? Чему равен \( \displaystyle x\) в такой точке?
В любой точке оси ординат (это название оси \( \displaystyle y\), если ты забыл) \( \displaystyle x=0\).
Значит достаточно подставить \( \displaystyle x=0\) в функцию, и получим ординату пересечения графика с осью \( \displaystyle y\):
\( \displaystyle y=k\cdot 0+b=b\)
Теперь по поводу \( \displaystyle k\). Рассмотрим функцию \( \displaystyle \left( b=0 \right).\) Будем менять \( \displaystyle k\) и смотреть, что происходит с графиком.
Так, теперь ясно: \( \displaystyle k\) влияет на наклон графика.
Чем больше \( \displaystyle k\) по модулю (то есть несмотря на знак), тем «круче» (под большим углом к оси абсцисс – \( \displaystyle Ox\)) расположена прямая.
Если \( \displaystyle k>0\), график наклонен «вправо», при \( \displaystyle k
Выберем на графике две точки \( \displaystyle A\) и \( \displaystyle B\). Для простоты выберем точку \( \displaystyle A\) на пересечении графика с осью ординат. Точка \( \displaystyle B\) – в произвольном месте прямой, пусть ее координаты равны \( \displaystyle \left( x;y \right)\).
Рассмотрим прямоугольный треугольник \( \displaystyle ABC\), построенный на отрезке \( \displaystyle AB\) как на гипотенузе.
Из рисунка видно, что \( \displaystyle AC=x\), \( \displaystyle BC=y-b\).
Подставим \( \displaystyle y=kx+b\) в \( \displaystyle BC:BC=y-b=kx+b-b=kx\).
Получается, что \( BC = k \cdot AC<\rm< >> \Rightarrow <\rm< >>k = \frac<
Итак, коэффициент \( \displaystyle k\) равен тангенсу угла наклона графика, то есть угла между графиком и осью абсциссс.
Именно поэтому его (коэффициент \( \displaystyle k\)) обычно называют угловым коэффициентом.
В случае, когда \( k
Если же \( \displaystyle k=0\), тогда и \( <\mathop<\rm tg>\nolimits> \alpha = 0,\) следовательно \( \displaystyle \alpha =0\), то есть прямая параллельна оси абсцисс.
Понимать геометрическое значение коэффициентов очень важно, оно часто используется в различных задачах на линейную функцию.
Разбор еще трех задач на линейную функцию
1. Найдите коэффициенты \( \displaystyle k\) и \( \displaystyle b\) линейной функции, график которой приведен на рисунке. Запишите уравнение этой функции.
2. Найдите коэффициенты \( \displaystyle k\) и \( \displaystyle b\) линейной функции, график которой приведен на рисунке. Запишите уравнение этой функции.
3. График какой из функций изображен на рисунке?
Решение задачи №1
Коэффициент \( b\) найти проще простого – это ведь точка пересечения графика с осью \( \displaystyle Oy\):
Угловой коэффициент \( \displaystyle k\) – это тангенс угла наклона прямой.
Для его нахождения выберем две точки \( \displaystyle A\) и \( \displaystyle B\) на графике и построим прямоугольный треугольник с гипотенузой \( \displaystyle AB\):
Что обозначает k в линейной функции
Уравнение вида y = kx + b задается как парой переменных x и y, так и парой параметров k, b. Поэтому возник вопрос, возможно ли изобразить прямую из плоскости ху соответствующим ей объектом в плоскости параметров (k; b), что будет представлять собой этот объект, как будут изображены семейства прямых со схожими свойствами.
1) отображение графиков линейных функций на плоскости параметров;
2) определение семейства прямых, отображенных на плоскости параметров в виде прямых или областей;
1) научиться выполнять построения графиков линейных функций на плоскости параметров, и наоборот, уметь выполнить построение графика в плоскости ху по соответствующему объекту из плоскости параметров аb;
2) выяснить, какие семейства прямых из плоскости ху изображаются на плоскости параметров в виде прямых, в виде областей;
3) обобщить полученные результаты для правил построения любого семейства прямых.
Если прямые на плоскости (x; y) пересекаются в одной точке или параллельны, то соответствующие им точки на плоскости (k; b) лежат на одной прямой.
2) аналитико – синтетический.
Предмет исследования: отображение графиков линейных функций на плоскость параметров (k, b).
Объект исследования: график линейной функции.
Семейства прямых на координатной плоскости (х; у), соответствующих точкам плоскости (k; b)
Линейным уравнением с двумя переменными называется уравнение вида y = kx + b, где x и y – переменные, k, b – некоторые числа.
Графиком линейного уравнения с двумя переменными является прямая.
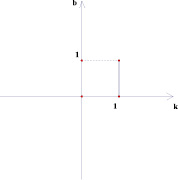
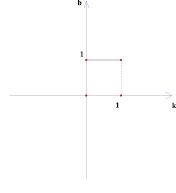
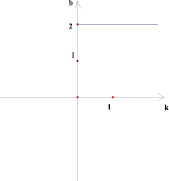
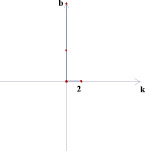
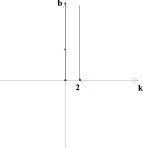
Рассмотрим координатную плоскость (k; b). Каждая прямая вида у = kх + b изображается на этой плоскости в виде точки с координатами (k; b).
Например, прямая у = 2х + 5 изображается на плоскости (k; b) в виде точки (2; 5), а прямая у = – 2 в виде точки (0; – 2).
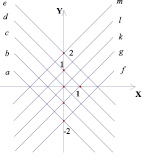
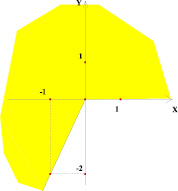
Выполняя построения графиков линейных функций на плоскости параметров, было замечено, что параллельные прямые отображаются на этой плоскости в виде точек, лежащих на одной прямой, перпендикулярной оси Оk (рис. 1).
Плоскость (x; y) Плоскость (k; b)
Действительно, у точек, лежащих на таких прямых координата k одинакова, а это коэффициент при х, по которому можно определить взаимное расположение графиков прямых на плоскости (x; y).
Чем ближе вертикальные прямые к началу координат, тем меньше угол наклона между возрастающими прямыми и осью Ох и больше угол наклона между убывающими прямыми и осью Ох (рис. 2).
На плоскости, кроме точек и прямых, можно изображать области (будем их выделять цветом).
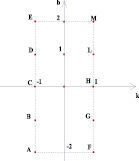
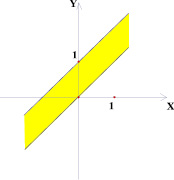
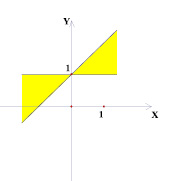
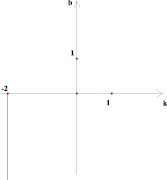
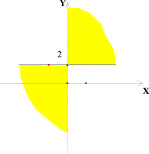
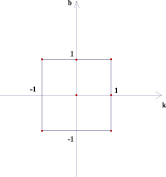
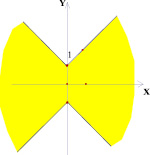
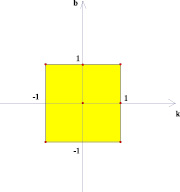
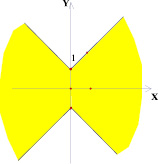
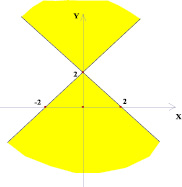
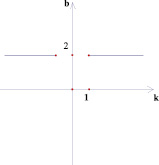
Рассмотрим следующую задачу: на координатной плоскости (k; b) изображено множество точек, соответствующее некоторому семейству прямых вида у = kх + b. На плоскости (х; у) все эти прямые покрашены. Изобразить на плоскости (х; у) получившуюся покрашенную область. Были получены следующие результаты (рис. 2–7).
Точки внутри квадрата на плоскости (k; b) в 5 и 6 случае имеют одинаковые закрашенные области на плоскости (х; у), потому что любая точка внутри квадрата лежит на отрезке, параллельном оси абсцисс плоскости (k; b) с концами на сторонах квадрата. На плоскости (х; у) это будет означать, что соответствующая выбранной точке прямая будет лежать в полосе между прямыми, соответствующими концам отрезка, то есть в покрашенной области.
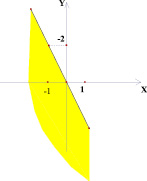
Исследуем обратную задачу: на координатной плоскости (х; у) покрашено некоторое семейство прямых. В результате на плоскости получилась покрашенная область. Изобразите на координатной плоскости (k; b) множество точек, соответствующее этому семейству прямых. Оказывается, в некоторых случаях это можно сделать не единственным образом (рис. 8–9).
Как видно из рис. 9 возможно несколько решений. Например, объединение луча (полуоси ординат в положительном направлении) и отрезка [0; 2] на оси абсцисс. Или объединение двух лучей: полуоси ординат в положительном направлении и параллельного луча с вершиной в точке (2; 0).
Прямая на плоскости (k; b)
Рассмотрим на плоскости (k; b) прямую b = k. Каждая точка этой прямой задает на плоскости (х; у) прямую, а вся прямая b = k задает на плоскости (х; у) семейство прямых. Для определения свойства семейства прямых сначала были взяты несколько конкретных точек на прямой b = k и построены соответствующие им прямые на плоскости (х; у). Оказалось, что все прямые проходят через точку (– 1; 0).
Докажем это утверждение. Так как b = k, то на плоскости (х; у) мы получаем семейство прямых вида у = kx + k. Если записать их в виде у = k(x + 1), то можно заметить, что все эти прямые проходят через точку (– 1; 0).
На координатной плоскости (k; b) проведем три прямые, проходящие через одну точку. Каждая такая прямая изображает пучок прямых на плоскости (х; у). Три точки на плоскости (х; y), через которые проходят соответствующие пучки прямых, сами лежат на одной прямой.
На координатной плоскости (k; b) проведем три параллельные прямые. Каждая такая прямая изображает некоторое семейство прямых на плоскости (х; у). Три точки на плоскости (х; y), через которые проходят соответствующие пучки прямых, также лежат на одной прямой.
В случае пересечения три точки лежат на наклонной прямой, а в случае параллельности прямая вертикальна.
Можно сделать вывод, что три параллельные прямые и три прямые, имеющие общую точку, ведут себя одинаково (их образы лежат на одной прямой). Если договориться считать, что параллельные прямые также имеют общую точку – бесконечно удалённую, то не надо будет рассматривать эти два случая отдельно.
В ходе исследования были выполнены построения графиков линейных функций на плоскости параметров, и наоборот, выполнены построения графика в плоскости (х; у) по соответствующему объекту из плоскости параметров (k; b). Графики и их образы выполнялись как вручную, так и с помощью программы «Математический конструктор».
Были сделаны следующие выводы:
– семейство пересекающихся прямых в одной точке из плоскости (х; у) изображается на плоскости параметров в виде прямой;
– замкнутая область из плоскости параметров представляет собой закрашенную область, ограниченную двумя парами пресекающихся прямых;
– образы параллельных прямых лежат на одной прямой, перпендикулярной оси Оk в плоскости параметров.
Одинаковое поведение образов параллельных прямых и прямых, имеющих общую точку (лежат на одной прямой), позволяет не рассматривать эти случаи отдельно, если считать, что параллельные прямые также имеют общую точку – бесконечно удалённую.
Было доказано, что прямая b = k задает на плоскости (х; у) семейство пересекающихся прямых, проходящих через точку (– 1; 0).
Предположение о том, что если прямые на плоскости (x; y) пересекаются в одной точке или параллельны, то соответствующие им точки на плоскости (k; b) лежат на одной прямой, подтвердилось.
Результаты исследования можно использовать на факультативных занятиях в старших классах при введении понятия проективной плоскости, а также для углубленного изучения свойств графиков линейной функции.
Планируется создать программу для построения образов линейной функции на плоскости параметров и для обратной задачи.