Что обозначает каждая цифра в записи чисел

4 класс. Моро. Учебник №1. Ответы к стр. 25

Авг 18

4 класс. Моро. Учебник №1. Ответы к стр. 25

Числа от 1 до 1000

Числа, которые больше 1000
Нумерация

Ответы к стр. 25

100. Запиши и прочитай числа, в которых:
1) 30 единиц II класса и 870 единиц I класса;

2) 8 единиц II класса и 600 единиц I класса;

3) 104 единицы II класса, а единицы I класса отсутствуют.

356 409 км, 406 740 км

2) Что обозначает каждая цифра в записи этих чисел?

356 409 (три единицы разряда сотен тысяч, пять единиц разряда десятков тысяч, 6 единиц разряда единиц тысяч, 4 единицы разряда сотен, 9 единиц).

406 740 (4 единицы разряда сотен тысяч, 6 единиц разряда единиц тысяч, 7 единиц разряда сотен, 4 единицы разряда десятков).

95. Замени данные числа суммой по образцу.

108 201 = 108 000 + 201 91 007 = 91 000 + 7
360 400 = 360 000 + 400 50 070 = 50 000 + 70

804 : 4 = 201 627 : 3 = 209

103. Купили 3 пакета семян тыквы, по 200 г в каждом, и 3 пакета семян укропа, по 100 г в каждом. На сколько граммов больше купили семян тыквы, чем семян укропа?

Последняя таблетка будет принята через 4 часа.

Запиши цифрами число восемьсот две тысячи тридцать восемь.

ЗАДАНИЕ НА ПОЛЯХ:
Цепочка

Источник

Учебник Моро 4 класс 1 часть. Страница 25

Упражнения:

100. Запиши и прочитай числа, в которых:

101. 1) Запиши числа цифрами.

Наименьшее расстояние от Земли до Луны составляет триста пятьдесят шесть тысяч четыреста девять километров, а наибольшее — четыреста шесть тысяч семьсот сорок километров.

2) Что обозначает каждая цифра в записи этих чисел?

102. Реши:

103. Купили 3 пакета семян тыквы, по 200 г в каждом, и 3 пакета семян укропа, по 100 г в каждом. На сколько граммов больше купили семян тыквы, чем семян укропа?

1) 200 • 3 = 600 (г) — семян тыквы.

2) 100 • 3 = 300 (г) — семян укропа.

3) 600 — 300 = 300 (г) — семян тыквы больше, чем семян укропа.

104. До обеденного перерыва в магазине продали 3 мешка сахарного песка, по 45 кг в каждом, а после перерыва — 5 таких мешков.

Объясни, что означают выражения:

45 • 5 — 45 • 3 — на сколько больше кг сахара продали после перерыва на обед, чем до перерыва на обед.

45 • 5 + 45 • 3 — количество (в кг) всего проданного сахара за день.

105. Реши:

8 + 0 + 0 + 6 = 8 + 6 = 14
8 — 0 + 0 • 6 = 8 — 0 + 0 = 8

9 — 0 — 6 • 1 = 9 — 0 — 6 = 9 — 6 = 3
9 + 0 + 6 : 1 = 9 + 0 + 6 = 15

0 : 7 + 0 • 5 + 3 = 0 + 0 + 3 = 3
7 : 7 — 0 • (4 + 2) = 1 — 0 = 1

106. «Вот вам 3 таблетки, — сказал доктор. — Принимайте по одной через каждые 2 часа». Через сколько времени будет принята последняя таблетка?

2 + 2 = 4 (часа) — будет выпита последняя таблетка.

Ответ: через 4 часа.

Запиши цифрами число восемьсот две тысячи тридцать восемь — 802 038

Задание на полях

Цепочка:

Источник

Конспект урока в 4 классе на тему «Значение цифры в записи числа»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Тема урока: Значение цифры в записи числа.

Тип урока : изучение нового материала

Цель урока: Учить детей читать и записывать многозначные числа, показать, что обозначает каждая цифра в записи.

1. Совершенствовать вычислительные навыки умения решать задачи и уравнения.

2. Развивать мыслительные процессы (анализ, синтез, сравнение, память, внимание).

3. Развивать умение выполнять задания логического характера.

4. Воспитывать познавательный интерес.

для учителя: учебник, методическое пособие.

для учащихся: учебник, тетрадь, ручка.

Наглядность к уроку: карточки, опорные схемы.

У.: Здравствуйте, дети!

Прозвенел уже звонок,
Сядьте тихо и неслышно,
И скорей начнём урок.
Будем мы писать, трудиться,
Ведь заданья нелегки.
Нам, друзья, нельзя лениться,
Так как мы ученики.

У.: Найдите значение выражения удобным способом:

(Ученик выходит к доске, выполняет решение, затем вслух проговаривает.)

У.: Предлагаю провести

«Географо – математическую минутку».

У.: Поговорим сегодня о самых, самых, самых…

Вы запишите в тетрадь многозначные числа, которые прозвучат в предложении:

а) Самый крупный океан земного шара – Тихий океан или Великий.

б) Самое глубокое место в Тихом океане – Марианский желоб, Марианская впадина глубиной 11.034 метра.

в) Самое чистое и глубокое озеро – Байкал, его глубина 1741 метр.

г) Самый крупный материк земного шара – Евразия.

д) Самая высокая вершина – Эверест или Джомолунгма в Гималаях, ее высота 8848 метров.

Дети записывают числа в тетради, затем идет самопроверка. Ответы записаны на карточках, которые показывает учитель.

У.: Сколько единиц II класса в этих числах?

У.: Сколько сотен в числе 11034?

У.: Сколько всего сотен в этом числе?

У.: А если вы пропустите в записи числа цифру 0, то какое получится число?

У.: Чтобы не делать ошибки нужно прежде выяснить, сколько разрядных единиц в числе.

У.: Используя цифры 1 и 5, напишите четырехзначные

числа, в которых цифра 5 встречается один раз.

Ученик выходит к доске, записывает числа, проговаривая вслух.

Д.: 5111,1511, 1151, 1115.

У.: Какие числа встречались в задании?

Д: Многозначные числа.

Ученики давали верные ответы.

У.: Сегодня мы откроем еще один секрет многозначных чисел. Будем говорить о значении цифры в записи числа.

У.: Давайте понаблюдаем, как путешествует по числам цифра 5.

У.: В числе 5111 – 5 это?

У.: В числе 1511 – 5 это?

У.: В числе 1151 – 5 это?

У.: В числе 1115 – 5 это?

У.: От чего же зависит значение цифры?

Д.: От места, которое она занимает.

У.: Правильно, также говорят, что значение цифры зависит от позиции, которую она занимает.

Дети читают параграф на стр. 22. Объяснение материала.

У.: Выполните упр. 97 на стр.24.

У.: Разбейте число на классы. Скажите, сколько в нем единиц каждого класса:

7300 29608 305220 400400 90060

7340 29680 305020 400004 60090

Дети объясняют с места.

У.: Запишите и прочитайте числа, в которых:

1) 30 единиц II класса и 870 единиц I класса;

2) 8 единиц II класса и 600 единиц I класса;

3) 104 единицы II класса, а единицы I класса отсутствуют.

Дети выполняют задание с комментированием у доски.

У.: Запишите числа цифрами:

Наименьшее расстояние от Земли до Луны составляет триста пятьдесят шесть тысяч четыреста девять километров, а наибольшее – четыреста шесть тысяч семьсот сорок километров.

Что обозначает каждая цифра в записи этих чисел?

Дети записывают числа и объясняют с места, учитель показывает карточки.

У.: Вы устали, мы немного отдохнем!

а) За 5 м ткани заплатили с руб. Сколько стоит 1 метр?

б) Купили 3 одинаковых коробки конфет, всего x граммов. Сколько весит одна коробка?

в) На клумбе распустилось а ирисов и в пионов. На сколько больше распустилось пионов?

г) В одном ящике х груш, а в другом у кг слив. Во сколько раз груши тяжелее слив?

Ученики называют выражения, учитель показывает карточки.

У.: Прочитайте задачу:

В альбоме 100 листов. Сколько таких альбомов получится из 15000 листов? Сколько листов в 1000таких альбомов?

Сделайте краткую запись и решите ее.

1) 1 а. – 100 л. 2) 1а. – 100 л.

Решение самостоятельное. Один ученик решает у доски.

У.: Найдите упр. 130 на стр.28. Решите уравнения:

У.: Первую строку решают 1 вариант, вторую строку – 2 вариант.

У.: Вспомните, как найти неизвестное слагаемое? уменьшаемое? Вычитаемое?

Учитель показывает опорные схемы. (См. Приложение)

Проводится взаимопроверка в парах.

У.: Упражнение 126 решите самостоятельно.

1) Числа 57, 90, 200 увеличь в 10 раз, в 100 раз.

2) Числа 4000, 60000, 152000 уменьши в 1000 раз.

Ученики комментируют у доски.

1) 57*10=570 90*10=900 200*10=2000

57*100=5700 90*100=9000 200*100=20000

2) 4000:1000=4 60000:1000=60 152000:1000=152

У.: Откройте дневники, запишите домашнее задание.

У.: Что обозначает цифра 2 в числе 8342?

А в числе 35287? В числе 67827?

У.: От чего зависит значение цифры?

У.: Ребята, что вы сегодня делали на уроке?

У.: Что вы нового узнали на уроке?

1. О. А. Мокрушина, О.И. Дмитриева. Математика 4 класс: Поурочные разработки к учебнику М. И. Моро, М. А. Бантовой и др. – М.: ВАКО, 2003. – 400 с.

2. Математика. Учебник для 4 класса начальной школы в 2 ч. Ч. 1 (Первое полугодие)/ (М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.). – 2 –е изд. – М.: Просвещение, 2005. – 112 с.

3. Программа «Школа России», А.А. Плешаков, 2005.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-688400

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Госдума приняла закон об использовании онлайн-ресурсов в школах

Время чтения: 2 минуты

В Оренбурге школьников переведут на дистанционное обучение с 9 декабря

Время чтения: 1 минута

Псковских школьников отправили на дистанционку до 10 декабря

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Разряды и классы чисел

Числа и цифры

Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.

Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …

От количества цифр в числе зависит его название.

Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.

Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.

Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.

Каждая цифра в записи многозначного числа занимает определенное место — позицию.

Классы чисел

Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.

Названия классов многозначных чисел справа налево:

Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:

А теперь прочитаем число единиц каждого класса слева направо:

Разряды чисел

От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:

Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.

Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.

У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.

Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.

Низший (младший) разряд многозначного натурального числа — разряд единиц.

Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.

Разрядные единицы обозначают так:

Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.

Чтобы легче понимать математику — записывайтесь на наши курсы по математике!

Потренируемся

Пример 1. Записать цифрами число, в котором содержится:

Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:

Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.

Пример 2. Сколько сотен содержится в числе 6284?

В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.

Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.

Значит, в данном числе содержится 62 сотни.

Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.

Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:

Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.

Источник

Что обозначает каждая цифра в записи чисел

*Заочная математическая школа

Составитель преподаватель КубГУ Соколова И.В.

Тема 1. Десятичная запись натурального числа.

Первые представления о числе приобретены людьми с незапамятной древности. Они возникли изсчета людей, животных, плодов, различных изделий человека и других предметов. Результатом счета являются числа 1, 2, 3, 4, 5,… Этот ряд продолжается без конца; он называется натуральным рядом, а числа–натуральными.

Способы записи чисел называют системами счисления. Нашу систему счисления называют позиционной, т.к. каждая из цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) имеет различное значение в зависимости от позиции цифры в записи числа. Например, каждая цифра 3 в записи числа 333 имеет различное числовое значение: первая слева обозначает 3 сотни, вторая – 3 десятка, третья – 3 единицы. За основание нашей системы счисления взято число 10, поэтому она называется десятичной.

Любое натуральное число в десятичной системе счисления можно записать в виде суммы числа единиц, десятков, сотен и т.д. Например, запись 27 354 выражает, что в составе числа имеются 4 единицы, 5 десятков, 3 сотни, 7 тысяч и 2 десятка тысяч. В виде суммы оно запишется так:

27 354=2 · 10 000 + 7 · 1 000 + 3 · 100 + 5 · 10 + 4.

.

Двузначное число разделили на его первую цифру. В результате получили 14. Найти все такие двузначные числа.

У трехзначного числа поменяли местами последние 2 цифры. В результате число уменьшилось на 18. Найдите это число.

Тема 2. Деление с остатком.

Известно, что всякое натуральное число a можно разделить на другое натуральное число b с остатком, т.е. единственным образом представить a в виде:

В страну Арифметику прибыла “делегация” чисел, при делении которых на 11 получались частные равные остаткам. Какой вид имели эти числа и сколько их было?

Тема 3. Правила нахождения остатков.

Рассмотрим правила нахождения остатков при делении натуральных чисел на 2, 3, 4, 5, 10, 25:

1. Число делится на 2 (на 5, на 10), если его последняя цифра делится на 2 (на 5, на 10);

2. Число делится на 4 (на 25), если число, записанное двумя его последними цифрами, делится на 4 (на 25);

3. Число делится на 3 (на 9), если сумма его цифр делится на 3 (на 9).

Упражнение 2. Получить указанные правила на примере делимости трехзначных чисел.

Решение. Воспользуемся свойством: если и , то

1. . Пусть левая часть равенства делится на 2, тогда так как в правой части первое слагаемое делится на 2 (в разложении его на множители есть число 2), то число c тоже должно делиться на 2. Получили. что последняя цифра c числа делится на 2. Аналогично доказывается для делимости на 5 и 10 (доказательство провести самостоятельно).

2. . Пусть делится на 4. Так как в правой части 100 × а делится на 4, то тоже должно делится на 4, т.е., число, записанное двумя последними цифрами делится на 4.

3.. Пусть . Так как в правой части то a+b+c тоже должно делится на 3. Получили что сумма цифр числа делится на 3. Докажите самостоятельно для делимости на 9.

Сформулируйте признаки делимости чисел на 2, 3, 4, 5, 10, 25.

Упражнение 3. Докажите, что если в трехзначном числе средняя цифра равна сумме крайних, то число делится на 11.

Решение. Если цифры числа (слева направо) a, a+b, b, то само число: .

Получили, что в разложении числа на множители есть 11, следовательно, число делится на 11.

Из трех различных цифр, отличных от нуля составили всевозможные двузначные числа так, что цифры в записи числа не повторялись. Докажите, что сумма всех полученных чисел делится на 22 независимо от исходного выбора цифр.

Докажите, что число составное.

Если натуральные числа a и b делятся на некоторое натуральное число d, то d называется их общим делителем. Наибольший из общих делителей называется их наибольшим общим делителем и обозначается НОД(a, b). Если НОД(a, b)=1, то числа a и b называют взаимно простыми.

Упражнение 4. Найти все пятизначные числа вида 34x5y, каждое из которых делится на 36.

Решение. Число 36 можно представить в виде произведения взаимно простых чисел 9 и 4, следовательно, искомые числа делятся на 4 и 9. Число 5y должно делиться на 4, значит y=2 или y=6. 3+4+x+5+y=12+x+y должно делится на 9. При y=2 находим такую цифру x, чтобы , отсюда x=4. При y=6 , отсюда x=0 или x=9. Значит, условию задачи удовлетворяют три числа: 34 452, 34 056, 34 956.

Чтобы получить доступ к секретной информации компьютера, необходимо набрать код – четырехзначное число. Известно, что 1-я и 3-я цифра кода – единицы, а все число делится на 15, но не делится на 2. Найдите минимальное количество кодов, которые нужно перебрать, чтобы обнаружить искомый код.

Тема 4. Алгоритм Евклида.

Для разыскания НОД чисел применяется и другой метод. Он называется алгоритмом Евклида. Познакомимся с алгоритмом Евклида на примерах.

а) НОД(6621,111); б) НОД(40,5).

а) Делим 6621 на 111 с остатком:

Теперь делим делитель 111 на остаток 72:

Снова делим делитель на остаток и т.д.

Процесс закончен, если на некотором шаге получаем остаток, равный нулю. НОД данных чисел равен последнему отличному от нуля остатку в алгоритме Евклида. В нашем случае это 3, т.е. НОД(6621,111)=3. Процесс, описанный в алгоритме Евклида не бесконечен, так как остатки убывают, оставаясь неотрицательными, а самый маленький из них ноль: 72>39>33>6>3>0=0.

б) Разделим 40 на 5: 40=5·8+0. На первом шаге получили остаток 0. В этом случае НОД(40,5) равен меньшему из чисел, т.е. 5.

Если натуральное число k делится на числа a и b, то оно называется общим кратным чисел a и b. Наименьшее из таких общих кратных называется наименьшим общим кратным чисел a и b и обозначается НОК(a, b).

НОК двух чисел равно их произведению, деленному на их НОД, т.е.

Пользуясь алгоритмом Евклида, найдите НОД и НОК номера вашего дома и почтового индекса.

Из победителей математической олимпиады был сформирован отряд, в котором больше 100, но меньше 150 детей. Для отправки в летнюю математическую школу их разместили вначале в 8, а затем в 10 автобусах. При этом в обоих случаях детей в автобусах оказалось поровну. Сколько в отряде было девочек и мальчиков, если девочек было на 40 человек меньше, чем мальчиков?

Для учеников трех шестых классов школа к новогоднему вечеру закупила шоколадные конфеты: 390, 405 и 420 штук. Сколько подарков получил каждый класс, если в каждом подарке одинаковое количество конфет и число их – наибольшее из всех возможных.

а) б) в) ; г)

Даны две равные дроби. Одна из них , а сложив числитель со знаменателем второй дроби, получили 91. Найдите вторую дробь.

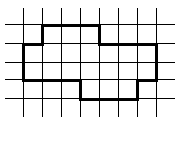
Укажите различные способы разрезания данной фигуры на 4 равные части, чтобы линия разреза шла по сторонам клеток. (Способы считаются различными, если части, получаемые при одном способе разрезания не равны частям, полученным при другом способе).

Источник