Что обозначает r в технической механике

Теоретическая механика. В помощь студенту

Теоретическая механика – это раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел.

Теоретическая механика является наукой, в которой изучаются перемещения тел с течением времени (механические движения). Она служит базой других разделов механики (теория упругости, сопротивление материалов, теория пластичности, теория механизмов и машин, гидроаэродинамика) и многих технических дисциплин.

Механическое движение — это изменение с течением времени взаимного положения в пространстве материальных тел.

Механическое взаимодействие – это такое взаимодействие, в результате которого изменяется механическое движение или изменяется взаимное положение частей тела.

Статика твердого тела

Статика — это раздел теоретической механики, в котором рассматриваются задачи на равновесие твердых тел и преобразования одной системы сил в другую, ей эквивалентную.

Основные понятия и законы статики

Кинематика

Кинематика — раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела.

Основные понятия кинематики

Динамика

Динамика — это раздел теоретической механики, в котором изучаются механические движении материальных тел в зависимости от причин, их вызывающих.

Основные понятия динамики

Примеры решения задач

Решение примеров по теме: «Статика твердого тела»

Пример 1. Условия равновесия

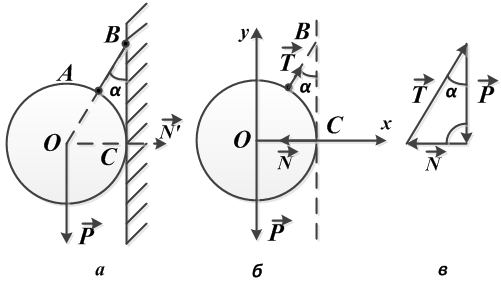
Висящий на нити, под углом в сорок пять градусов к гладкой стене шар весом в десять Ньютон, находится в состоянии равновесия (рис. а). Необходимо определить давление однородного шара на гладкую стенку и натяжение нити.

Решение.
Отбрасываем связи, а их действие на шар заменяем реакциями.
Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т — вдоль нити от точки А к точке В.
Тем самым выявляется полная система сил, приложенных к покоящемуся шару.

Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. б).

Реакции N и Т по величине неизвестны. Для их определения следует воспользоваться условиями равновесия (в той или иной форме — геометрической, аналитической).

При геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема синусов, теорема косинусов, теорема Пифагора и т.д.).

В данном случае это замкнутый силовой треугольник (рис. в), из которого получаем:

После подстановки в формулы числовых значений, получим:
.

Ответ: .

Решение примеров по теме: «Кинематика»

Пример 2. Уравнение траектории точки

Дано:
Движение точки задано уравнениями ;
(x, у — в сантиметрах, t — в секундах).
Найти: уравнение траектории точки в координатной форме.

Решение. Для определения уравнения траектории из уравнений движения исключаем время t. Для этого из первого уравнения выражаем и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:
.

Опуская промежуточные выражения, получаем уравнение траектории:
.

Ответ: .

Решение примеров по теме: «Динамика»

Пример 3. Основной закон динамики точки

Свободная материальная точка, масса которой десять килограмм, движется прямолинейно с ускорением пол метра в секунду в квадрате. Определить силу, приложенную к точке.

Решение.
Согласно основному закону динамики: .

Подставив значения в формулу, получим:

В помощь студенту

Формулы, правила, законы, теоремы, уравнения, примеры решения задач

Список литературы:
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах.
Буторин Л.В., Бусыгина Е.Б. Теоретическая механика. Учебно-практическое пособие.

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Обозначения

Какие обозначения приняты в сопромате?

А – площадь поперечного сечения брутто, м 2 ;

а – размер стороны прямоугольника, м;

а – расстояние между параллельными осями, м;

а – длина силового участка, м;

а – ордината эпюры изгибающих моментов, Нм;

b – расстояние между параллельными осями, м;

b – ширина сечения, м;

b – ордината эпюры изгибающих моментов, Нм;

С – центр тяжести сечения;

с – размер сечения или его части, м;

с – длина силового участка, м;

с – ордината эпюры изгибающих моментов, Нм;

D – диаметр наружный сечения, м;

d– ордината эпюр изгибающих моментов, м;

d– диаметр внутренний сечения, м;

Е – модуль упругости I рода, модуль Юнга, Па;

F – сила, Н;

— 1 единичная сила, н;

G – модуль сдвига, Па;

g – ускорение свободного падения (м/с 2 );

Н – высота падения ударяющего тела, м;

I_x, I_y – осевые моменты инерции сечения, м 4 ;

I_ρ – полярный момент инерции сечения, м 4 ;

I_max, I_min – главные центральные моменты инерции сечения, м 4 ;

i – индекс у сил и усилий;

k_σ, k_τ– эффективные коэффициенты концентрации напряжений, безразмерные;

ℓ — длина стержня или силового участка, м;

М – сосредоточенный момент, Нм;

М_х, М_у – изгибающие моменты (внутренние), Нм;

М_к – крутящий момент (внутренний, может обозначаться Т (фр.)).

М_к, М_н – значения внутренних изгибающих моментов в конце и начале силового участка, Нм;

— единичная пара сил,

N – нормальная или продольная сила (внутренняя), н;

n – коэффициент запаса прочности (может быть обозначен как k);

[n] или n_adm – допускаемый коэффициент запаса прочности;

[n_уст ] или n_{уст adm}– допускаемый коэффициент запаса на устойчивость;

n_в – скорость вращения вала, об/мин;

Р – полное напряжение, Па;

Q (Q_x, Q_y) – поперечная сила (внутренняя), н;

q – погонная нагрузка, н/м;

q_σ,q_τ – коэффициенты чувствительности к концентрации напряжений, безразмерная;

R – равнодействующая сил, н;

S_x, S_y – статические моменты площади сечения, м 3 ;

t_i – усилие в ветви ремня (ременной передачи), н;

u – удельная потенциальная энергия деформирования;

u_р – удельная потенциальная энергия изменения формы;

u_max, u_min – главные центральные оси;

u – перемещение в направлении оси Х, м;

v – перемещение в направлении оси у, м;

v – скорость ударяющего тела. м/с 2 ;

w – перемещение в направлении оси z, м;

W_i – мощность, передаваемая шестерней, колесом и т.п., кВт;

W_x, W_y – осевые моменты сопротивления, м 3;

W_ρ – полярный момент сопротивления, м 3 ;

W_к – момент сопротивления при кручении, м 3 ;

х – горизонтальная ось сечения;

у – вертикальная ось сечения;

х₀, у₀ – центральные оси сечения;

y_max – координата точки, наиболее удаленной от нейтральной линии;

[σ] или σ_adm – допускаемое напряжение, Па;

σ_к – критическое напряжение, Па;

τ (τ_ху, τ_уz, τ_zx) – касательное напряжение, Па;

φ – угол поворота сечения при кручении, град;

φ – коэффициент понижения допускаемого напряжения, безразмерный;

α – угол, определяющий положение осей, град;

α₀ – угол, определяющий положение главных центральных осей, град;

β_σ β_τ – коэффициент, учитывающий влияние качества поверхности на усталость, безразмерная;

γ – удельный вес, н/м 3 ;

∆ – перемещение (линейное, м; угловое, рад);

∆ℓ – абсолютная линейная деформация (удлинение или укорочение), м;

∆b – абсолютная поперечная деформация, м;

∆S – абсолютный сдвиг, м;

ε – относительная линейная деформация, безразмерная;

ε_пр, ε_поп – относительные продольная и поперечная деформации, безразмерные;

ε_σ ε_τ – коэффициенты, учитывающие влияние размеров деталей на предел выносливости, безразмерные;

θ – относительный (погонный) угол поворота, рад/м;

λ – гибкость стержня, безразмерная;

μ – коэффициент Пуассона, безразмерная;

ν – коэффициент приведения длины, безразмерная;

σ (σ_х, σ_у, σ_z) – нормальное напряжение, Па;

σ₁, σ₂, σ₃ – главные напряжения, Па;

σ_пр или σ_pr– предел пропорциональности, Па;

σ_т илиσ_у – предел текучести, Па;

σ_пр или σ_u– предел прочности, Па.

Источник

Тема 1.6. Основные понятия кинематики

§1. Кинематика точки. Введение в кинематику.

Кинематикой (от греческого «кинема» — движение) называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.

Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.

Для определения положения движущегося тела (или точки) в разные моменты времени с телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, образующую вместе с этим телом систему отсчета.

Рис.1. Система отчета

Изображать систему отсчета будем в виде трех координатных осей (не показывая тело, с которым они связаны).

Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем, как трехмерное евклидово пространство.

Время является скалярной, непрерывно изменяющейся величиной. В задачах кинематики время t принимают за независимое переменное (аргумент). Все другие переменные величины (расстояния, скорости и т. д.) рассматриваются как изменяющиеся с течением времени, т.е. как функции времени t.

Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано).

Основная задача кинематики точки твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих дан­ное движение.

Положение тела можно определить с помощью радиус-вектора или с помощью координат.

Рис.2. Радиус-вектор

Рис.3. Координаты точки М

Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.

Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движе­нии все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.

В дальнейшем под словом «тело» будем понимать «материальная точка».

Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. Вид траектории зависит от выбора системы отсчета.

В зависимости от вида траектории различают прямолинейное и криволинейное движение.

где и — радиус-векторы тела в эти моменты времени.Единицы измерения в системе СИ: м (метр).

Модуль перемещения не может быть больше пути: ≤s.

Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.

Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:

Видео-урок «Механическое движение»

§2. Способы задания движения точки

Для задания движения точки можно применять один из следую­щих трех способов:

1) векторный, 2) координатный, 3) естественный.

1. Векторный способ задания движения точки.

Рис.4. Движение точки М

При движении точки М вектор будет с течением времени изме­няться и по модулю, и по направлению. Следовательно, является переменным вектором (вектором-функцией), зависящим от аргу­мента t:

Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки.

2. Координатный способ задания движе­ния точки.

Положение точки можно непосредственно опре­делять ее декартовыми координатами х, у, z (рис.4), которые при движении точки будут с течением времени изменяться. Чтобы знать закон дви­жения точки, т.е. ее положение в пространстве в любой момент вре­мени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости

Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.

3. Естественный способ задания движе­ния точки.

Рис.5. Движение точки М

Естественным способом задания движения удобно пользоваться в тех слу­чаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ явля­ется траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.5) Выберем на этой траектории какую-нибудь неподвижную точку О’, которую примем за начало отсчета, и установим на траектории положительное и отрицатель­ное направления отсчета (как на координат­ной оси).

Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость s=f(t).

§3. Вектор скорости точки

Одной из основных кинематических характеристик движе­ния точки является векторная величина, называемая скоростью точки. Понятие скорости точки в равномерном прямолинейном движении относится к числу элементарных понятий.

Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с.

Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным.

Для равномерно-прямолинейного движения ∆r=v∆t, где v – постоянный вектор скорости.

Из соотношения видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени.

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Архив рубрики: Обозначения Сопромата

Изменения обозначений, принятых в сопромате, в соответствии с рекомендациями ИСО

Изменение русских индексов на латинские, соответствующие первым буквам аналогичного английского слова

Прочностные характеристики материала:

Напряжения:

Деформации:

Допускаемое значение величины обозначено не с помощью квадратных скобок, а с помощью индекса adm от англ. admissible — допускаемое

Применяемые индексы сокращений в сопромате

Применяемые индексы в обозначениях сопромата

Обозначения

Какие обозначения приняты в сопромате?

А – площадь поперечного сечения брутто, м 2 ;

а – размер стороны прямоугольника, м;

а – расстояние между параллельными осями, м;

а – длина силового участка, м;

а – ордината эпюры изгибающих моментов, Нм;

b – расстояние между параллельными осями, м;

b – ширина сечения, м;

b – ордината эпюры изгибающих моментов, Нм;

С – центр тяжести сечения;

с – размер сечения или его части, м;

с – длина силового участка, м;

с – ордината эпюры изгибающих моментов, Нм;

D – диаметр наружный сечения, м;

d– ордината эпюр изгибающих моментов, м;

d– диаметр внутренний сечения, м;

Е – модуль упругости I рода, модуль Юнга, Па;

F – сила, Н;

— 1 единичная сила, н;

G – модуль сдвига, Па;

g – ускорение свободного падения (м/с 2 );

Н – высота падения ударяющего тела, м;

I_x, I_y – осевые моменты инерции сечения, м 4 ;

I_ρ – полярный момент инерции сечения, м 4 ;

I_max, I_min – главные центральные моменты инерции сечения, м 4 ;

i – индекс у сил и усилий;

k_σ, k_τ– эффективные коэффициенты концентрации напряжений, безразмерные;

ℓ — длина стержня или силового участка, м;

М – сосредоточенный момент, Нм;

М_х, М_у – изгибающие моменты (внутренние), Нм;

М_к – крутящий момент (внутренний, может обозначаться Т (фр.)).

М_к, М_н – значения внутренних изгибающих моментов в конце и начале силового участка, Нм;

— единичная пара сил,

N – нормальная или продольная сила (внутренняя), н;

n – коэффициент запаса прочности (может быть обозначен как k);

[n] или n_adm – допускаемый коэффициент запаса прочности;

[n_уст ] или n_{уст adm}– допускаемый коэффициент запаса на устойчивость;

n_в – скорость вращения вала, об/мин;

Р – полное напряжение, Па;

Q (Q_x, Q_y) – поперечная сила (внутренняя), н;

q – погонная нагрузка, н/м;

q_σ,q_τ – коэффициенты чувствительности к концентрации напряжений, безразмерная;

R – равнодействующая сил, н;

S_x, S_y – статические моменты площади сечения, м 3 ;

t_i – усилие в ветви ремня (ременной передачи), н;

u – удельная потенциальная энергия деформирования;

u_р – удельная потенциальная энергия изменения формы;

u_max, u_min – главные центральные оси;

u – перемещение в направлении оси Х, м;

v – перемещение в направлении оси у, м;

v – скорость ударяющего тела. м/с 2 ;

w – перемещение в направлении оси z, м;

W_i – мощность, передаваемая шестерней, колесом и т.п., кВт;

W_x, W_y – осевые моменты сопротивления, м 3;

W_ρ – полярный момент сопротивления, м 3 ;

W_к – момент сопротивления при кручении, м 3 ;

х – горизонтальная ось сечения;

у – вертикальная ось сечения;

х₀, у₀ – центральные оси сечения;

y_max – координата точки, наиболее удаленной от нейтральной линии;

[σ] или σ_adm – допускаемое напряжение, Па;

σ_к – критическое напряжение, Па;

τ (τ_ху, τ_уz, τ_zx) – касательное напряжение, Па;

φ – угол поворота сечения при кручении, град;

φ – коэффициент понижения допускаемого напряжения, безразмерный;

α – угол, определяющий положение осей, град;

α₀ – угол, определяющий положение главных центральных осей, град;

β_σ β_τ – коэффициент, учитывающий влияние качества поверхности на усталость, безразмерная;

γ – удельный вес, н/м 3 ;

∆ – перемещение (линейное, м; угловое, рад);

∆ℓ – абсолютная линейная деформация (удлинение или укорочение), м;

∆b – абсолютная поперечная деформация, м;

∆S – абсолютный сдвиг, м;

ε – относительная линейная деформация, безразмерная;

ε_пр, ε_поп – относительные продольная и поперечная деформации, безразмерные;

ε_σ ε_τ – коэффициенты, учитывающие влияние размеров деталей на предел выносливости, безразмерные;

θ – относительный (погонный) угол поворота, рад/м;

λ – гибкость стержня, безразмерная;

μ – коэффициент Пуассона, безразмерная;

ν – коэффициент приведения длины, безразмерная;

σ (σ_х, σ_у, σ_z) – нормальное напряжение, Па;

σ₁, σ₂, σ₃ – главные напряжения, Па;

σ_пр или σ_pr– предел пропорциональности, Па;

σ_т илиσ_у – предел текучести, Па;

σ_пр или σ_u– предел прочности, Па.

Источник