Что обозначает т в матрице

От действий над матрицами к пониманию их сути…

Очень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья «Математика на пальцах», и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.

Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя). Сдаётесь? — тогда читаем дальше.

Сразу хочу сказать, что я не математик ни по образованию, ни по должности. Разве что мне интересна суть вещей, и я порой пытаюсь до них «докопаться». Так же было и с определителем: нужно было разобраться со множественной регрессией, а в этом разделе эконометрики практически всё делается через… матрицы, будь они неладны. Вот и пришлось мне самому провести небольшое исследование, поскольку ни один из знакомых математиков не дал внятного ответа на поставленный вопрос, изначально звучавший как «что такое определитель». Все утверждали, что определитель — это такое число, которое особым образом посчитано, и если оно равно нулю, то… В общем, как в любом учебнике по линейной алгебре. Спасибо, проходили.

Если какую-то идею придумал один человек, то другой человек должен быть в состоянии её понять (правда, для этого порой приходится вооружаться дополнительными знаниями). Обращение к «великому и могучему» поисковику показало, что «площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма». Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.

Получается, что для одномерного пространства определитель — это длина отрезка, для плоскости — площадь фигуры, для трёхмерной фигуры — её объём… дальше идут n-мерные пространства, вообразить которые нам не дано. Если объём фигуры (то есть определитель для матрицы 3*3) равен нулю, то это означает, что сама фигура не является трёхмерной (она может быть при этом двухмерной, одномерной или вообще представлять собой точку). Ранг матрицы — это истинная (максимальная) размерность пространства, для которого определитель не равен нулю.

Так, с определителем почти всё понятно: он определяет «объёмность» фигуры, образованной описанными системой уравнений векторами (хотя непонятно, почему его значение не зависит от того, имеем мы дело с исходной матрицей, или с транспонированной — возможно, транспонирование — это вид аффинного преобразования?). Теперь нужно разобраться с действиями над матрицами…

Если матрица — это система уравнений (а иначе зачем нам таблица каких-то цифр, не имеющих к реальности никакого отношения?), то мы можем с ней делать разные вещи. Например, можем сложить две строки одной и той же матрицы, или умножить строку на число (то есть каждый коэффициент строки умножаем на одно и то же число). Если у нас есть две матрицы с одинаковыми размерностями, то мы их можем сложить (главное, чтобы при этом мы не сложили бульдога с носорогом — но разве математики, разрабатывая теорию матриц, думали о таком варианте развития событий?). Интуитивно понятно, тем более что в линейной алгебре иллюстрациями подобных операций являются системы уравнений.

Однако в чём смысл умножения матриц? Как я могу умножить одну систему уравнений на другую? Какой смысл будет иметь то, что я получу в этом случае? Почему для умножения матриц неприменимо переместительное правило (то есть произведение матриц В*А не то что не равно произведению А*В, но и не всегда осуществимо)? Почему, если мы перемножим матрицу на вектор-столбец, то получим вектор-столбец, а если перемножим вектор-строку на матрицу, то получим вектор-строку?

Ну, тут уж не то что Википедия, — тут даже современные учебники по линейной алгебре бессильны дать какое-либо внятное объяснение. Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…

Если совокупность обычных векторов, т.е. направленных геометрических отрезков, является трёхмерным пространством, то часть этого пространства, состоящая из векторов, параллельных некоторой плоскости, является двумерным пространством, а все векторы, параллельные некоторой прямой, образуют одномерное векторное пространство.

В книгах об этом напрямую не говорится, но получается, что векторам, параллельным некоторой плоскости, необязательно лежать на этой плоскости. То есть они могут находиться в трёхмерном пространстве где угодно, но если они параллельны именно этой плоскости, то они образуют двумерное пространство… Из приходящих мне на ум аналогий — фотография: трёхмерный мир представлен на плоскости, при этом вектору, параллельному матрице (или плёнке) фотоаппарата, будет соответствовать такой же вектор на картинке (при условии соблюдении масштаба 1:1). Отображение трёхмерного мира на плоскости «убирает» одно измерение («глубину» картинки). Если я правильно понял сложные математические концепции, перемножение двух матриц как раз и представляет собой подобное отражение одного пространства в другом. Поэтому, если отражение пространства А в пространстве В возможно, то допустимость отражения пространства В в пространстве А — не гарантируется.

Любая статья заканчивается в тот момент, когда автору надоедает её писать. Поскольку я не ставил перед собой цели объять необъятное, а исключительно хотел понять суть описанных операций над матрицами и то, как именно матрицы связаны с решаемыми мной системами уравнений, я не полез в дальнейшие дебри линейной алгебры, а вернулся к эконометрике и множественной регрессии, но сделал это уже более осознанно. Понимая, что и зачем я делаю и почему только так, а не иначе. То, что у меня получилось в этом материале, можно озаглавить как «глава о сути основных операций линейной алгебры, которую почему-то забыли напечатать в учебниках». Но ведь мы же не читаем учебников, правда? Если честно, когда я учился в университете, мне очень не хватало именно понимания затронутых здесь вопросов, поэтому я надеюсь, что, изложив этот непростой материал по возможности простыми словами, я делаю доброе дело и помогаю кому-то вникнуть в саму суть матричной алгебры, переведя операции над матрицами из раздела «камлание с бубном» в раздел «практические инструменты, применяемые осознанно».

Источник

Матрицы: определение и основные понятия.

Определение матрицы

Количество строк и столбцов задают размеры матрицы.

Обозначение

A =		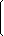4	1	-7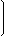
		-1	0	2

Элементы матрицы

Элементы матрицы A_4×4:

A =		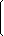4	1	-7	2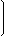
		-1	0	2	44
		4	6	7	9
		11	3	1	5

Демонстрация нулевых и ненулевых строк матрицы:

Демонстрация нулевых и ненулевых столбцов матрицы:

4

1

-7

не не нулевой столбец

Диагонали матрицы

Демонстрация главной и побочной диагонали матрицы:

Источник

Что обозначает т в матрице

ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ

Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:

Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.

В общем виде матрицу размером m×n записывают так

.

Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами a_ij: первый указывает номер строки, а второй – номер столбца. Например, a₂₃ – элемент стоит во 2-ой строке, 3-м столбце.

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.

Различаются также матрицы, имеющие только одну строку или один столбец.

Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.

Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,

.

Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

.

Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .

ДЕЙСТВИЯ НАД МАТРИЦАМИ

Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a_ij = b_ij. Так если и , то A=B, если a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁ и a₂₂ = b₂₂.

Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если , то .

Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.

Связь между матрицей A и её транспонированной можно записать в виде .

Например. Найти матрицу транспонированную данной.

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,

Примеры. Найти сумму матриц:

Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .

Для любых чисел a и b и матриц A и B выполняются равенства:

.

Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.

Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:

.

Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c₁₃, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.

В общем случае, если мы умножаем матрицу A = (a_ij) размера m×n на матрицу B = (b_ij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент c_ij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.

Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.

Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,

.

.

, B·A – не имеет смысла.

Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.

Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.

Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.

Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.

Например, если , то

.

Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов .

Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a₁₁a₂₂ – a₁₂a₂₁.

Определитель обозначается символом .

Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.

Примеры. Вычислить определители второго порядка.

Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.

Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:

.

Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a₁₁, a₁₂, a₁₃ и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.

Примеры. Вычислить определитель третьего порядка.

.

Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.

Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.

Источник

Основные сведения о матрицах

В этом разделе мы даем основные сведения о матрицах, необходимые для понимания статистики и анализа данных.

Матрицей размера m x n (читается m на n) называется прямоугольная таблица чисел, содержащая m строк и n столбцов.

Числа, составляющие матрицу, называются элементами матрицы.

В сокращенной записи обозначаем A =( a_ij ); i =1,2,… m ; j =1,2,…, n

Приведем пример матрицы 2 на 2:

Наряду с круглыми скобками используются и другие обозначения матрицы:

Две матрицы A и B одного размера называются равными, если они совпадают поэлементно, a_ij = b_ij для любых i =1,2,… m ; j =1,2,… n

Виды матриц

B=

Например,

Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.

Операции над матрицами

1. Умножение матрицы на число. Произведение матрицы А на число называется матрица B=A, элементы которой b_ij=a_ij для i=1,2,…m; j=1,2,…n

Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы.

В частности, произведение матрицы А на число 0 есть нулевая матрица.

2. Сложение матриц. Суммой двух матриц А и В одинакового размера m называется матрица С=А+В, элементы которой c_ij=a_ij+b_ij для i=1,2,…m; j=1,2,…n (т.е. матрицы складываются поэлементно).

4. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц A_m ∙B _kназывается такая матрица C_m, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:

Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из этих операций):

Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:

a) Если АВ существует, то после перестановки сомножителей местами произведение матриц ВА может и не существовать.

b) Если АВ и ВА существуют, то они могут быть матрицами разных размеров.

Из определения следует, что если матрица А имеет размер m , то транспонированная матрица А’ имеет размер n

В литературе встречаются и другие обозначения транспонированной матрицы, например, А Т

Источник

• ← Что обозначает считать ворон
• Что обозначает т1 и т2 на электросчетчике →

	0	1	-7
	0	0	2