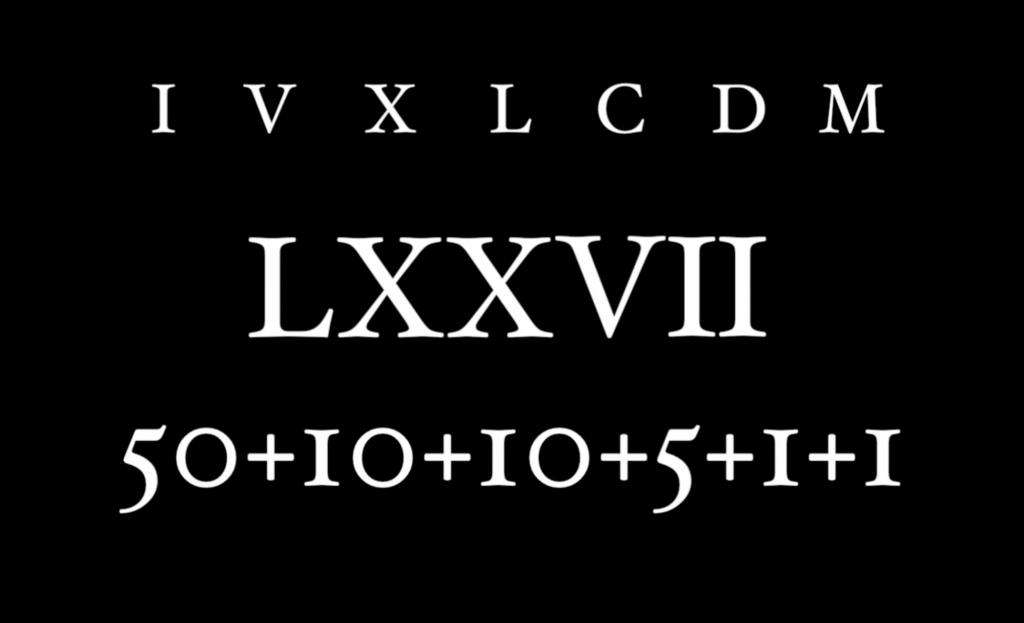Что обозначают римскими цифрами

Римские цифры

Системы счисления в культуре
Индо-арабская система счисления
Арабская Индийские Тамильская Бирманская	Кхмерская Лаоская Монгольская Тайская
Восточноазиатские системы счисления
Китайская Японская Сучжоу Корейская	Вьетнамская Счётные палочки
Алфавитные системы счисления
Абджадия Армянская Ариабхата Кириллическая	Греческая Эфиопская Еврейская Катапаяди
Другие системы
Вавилонская Египетская Этрусская Римская	Аттическая Кипу Майская
Позиционные системы счисления
Десятичная система счисления (10)
2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60
Нега-позиционная система счисления
Симметричная система счисления
Смешанные системы счисления
Фибоначчиева система счисления
Непозиционные системы счисления
Единичная (унарная) система счисления
Список систем счисления

Римские цифры — цифры, использовавшиеся древними римлянами в своей непозиционной системе счисления.

Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая — перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры.

Римские цифры появились за 500 лет до нашей эры у этрусков.

Содержание

Цифры

1	I	лат. unus
5	V	лат. quinque
10	X	лат. decem
50	L	лат. quinquaginta
100	C	лат. centum
500	D	лат. quingenti
1000	M	лат. mille

В русском языке для закрепления в памяти буквенных обозначений цифр в порядке убывания существуют мнемонические правила:

Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам

Соответственно M, D, C, L, X, V, I

Примеры

Число	Римское обозначение	Примечание
0	—
4	IV	до XIX века — IIII
8	VIII
9	IX
31	XXXI
46	XLVI
99	XCIX
583	DLXXXIII
888	DCCCLXXXVIII	от 1 до 1000 — самое длинное
1668	MDCLXVIII
1989	MCMLXXXIX
2010	MMX
2011	MMXI
2012	MMXII
3999	MMMCMXCIX
5000	ↁ
10 000	ↂ

Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.

При этом некоторые из цифр (I, X, C, M) могут повторяться, но не более трёх раз; таким образом, с их помощью можно записать любое целое число не более 3999 (MMMCMXCIX). В ранние периоды существовали знаки для обозначения бо́льших цифр — 5000, 10 000, 50 000 и 100 000 [источник не указан 683 дня] (тогда максимальное число по упомянутому правилу равно 399 999). При записи чисел в римской системе счисления меньшая цифра может стоять справа от большей; в этом случае она прибавляется к ней. Например, число 283 по-римски записывается как CCLXXXIII, то есть 100+100+50+30+3=283. Здесь цифра, изображающая сотню, повторена два раза, а цифры, изображающие соответственно десяток и единицу, повторены по три раза.

Пример: число 1988. Одна тысяча M, девять сотен CM, восемь десятков LXXX, восемь единиц VIII. Запишем их вместе: MCMLXXXVIII.

Повсеместно записывать число «четыре» как «IV» стали только в XIX веке, до этого наиболее часто употреблялась запись «IIII». Однако запись «IV» можно встретить уже в документах манускрипта «Forme of Cury», датируемых 1390 годом. На циферблатах часов в большинстве случаев традиционно используется «IIII» вместо «IV», главным образом, по эстетическим соображениям: такое написание обеспечивает визуальную симметрию с цифрами «VIII» на противоположной стороне, а перевёрнутую «IV» прочесть труднее, чем «IIII».

Меньшая цифра может быть записана и слева от большей, тогда её следует вычесть из большей. В этом случае повторения меньшей цифры не допускаются. По-римски число 94 будет XCIV=100-10+5-1=94 — так называемое «правило вычитания» (появилось в эпоху поздней античности, а до этого римляне писали число 4 как IIII, а число 40 — как XXXX). Существует шесть вариантов использования «правила вычитания»:

Необходимо отметить, что другие способы «вычитания» не допустимы; так, число 99 должно быть записано как XCIX, но не как IC. Однако, в наши дни в некоторых случаях используется и упрощенная запись римских чисел: например, в программе Microsoft Excel при преобразовании арабских цифр в римские при помощи функции «РИМСКОЕ()» можно использовать несколько видов представления чисел, от классического до сильно упрощенного (так, число 499 может быть записано как CDXCIX, LDVLIV, XDIX, VDIV или ID). Упрощение состоит в том, что для уменьшения какой-либо цифры слева от неё может писаться любая другая цифра:

С помощью римских цифр можно записывать и большие числа. Для этого над теми цифрами, которые обозначают тысячи, ставится черта, а над цифрами, которые обозначают миллионы, — двойная черта. Например, число 123123 будет выглядеть так:

Применение

В русском языке римские цифры используются в следующих случаях:

Римские цифры широко употреблялись в СССР при указании даты для обозначения месяца года: 11/III-85 или 9.XI.89. Для указания дат жизни и смерти на надгробиях часто использовался особый формат, где месяц года также обозначался римскими цифрами. С переходом на компьютерную обработку информации форматы даты, основанные на римских цифрах, практически вышли из употребления.

В других языках сфера применения римских цифр может иметь особенности, например, в западных странах римскими цифрами иногда записывается номер года.

Если разложить цифры графически, то получается следующее:

№

I

I

I

I

V

I

I

I

I

X

I

I

I

I

V

I

I

I

I

X

I

I

I

I

V

I

I

I

I

X

I

I

I

I

V

I

I

I

I

X

I

I

I

I

V

I

I

I

I

L

I

I

I

I

V

I

I

I

I

X

1

I

2

I

I

3

I

I

I

4

I

V

5

V

6

V

I

7

V

I

I

8

V

I

I

I

9

I

X

10

X

11

X

I

12

X

I

I

13

X

I

I

I

14

X

I

V

15

X

V

16

X

V

I

17

X

V

I

I

18

X

V

I

I

I

19

X

I

X

20

X

X

21

X

X

I

22

X

X

I

I

23

X

X

I

I

I

24

X

X

I

V

25

X

X

V

26

X

X

V

I

27

X

X

V

I

I

28

X

X

V

I

I

I

29

X

X

I

X

30

X

X

X

31

X

X

X

I

32

X

X

X

I

I

33

X

X

X

I

I

I

34

X

X

X

I

V

35

X

X

X

V

36

X

X

X

V

I

37

X

X

X

V

I

I

38

X

X

X

V

I

I

I

39

X

X

X

I

X

40

X

L

41

X

L

I

42

X

L

I

I

43

X

L

I

I

I

44

X

L

I

V

45

X

L

V

46

X

L

V

I

47

X

L

V

I

I

48

X

L

V

I

I

I

49

X

L

I

X

50

L

и т. д. до MMMCMXCIX (3999)

Юникод

Римские цифры в Юникод

Код	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Значение [4]	1	2	3	4	5	6	7	8	9	10	11	12	50	100	500	1 000
U+2160	Ⅰ 2160	Ⅱ 2161	Ⅲ 2162	Ⅳ 2163	Ⅴ 2164	Ⅵ 2165	Ⅶ 2166	Ⅷ 2167	Ⅸ 2168	Ⅹ 2169	Ⅺ 216A	Ⅻ 216B	Ⅼ 216C	Ⅽ 216D	Ⅾ 216E	Ⅿ 216F
U+2170	ⅰ 2170	ⅱ 2171	ⅲ 2172	ⅳ 2173	ⅴ 2174	ⅵ 2175	ⅶ 2176	ⅷ 2177	ⅸ 2178	ⅹ 2179	ⅺ 217A	ⅻ 217B	ⅼ 217C	ⅽ 217D	ⅾ 217E	ⅿ 217F
Значение	1 000		5 000		10 000		—	—	6		50		50 000		100 000
U+2160! U+2180	ↀ 2180		ↁ 2181		ↂ 2182		Ↄ	ↄ	ↄ		ↄ		ↄ		ↄ

Отображение всех этих символов требует наличия программного обеспечения, поддерживающего стандарт Юникод, и шрифта, содержащего соответствующие этим символам глифы.

Регулярные выражения

Регулярное выражение для проверки римских цифр — ‘^(?i)M<0,3>(D?C<0,3>|C[DM])(L?X<0,3>|X[LC])(V?I<0,3>|I[VX])$’. В языке Perl для поиска римских цифр в строке можно использовать регулярное выражение ‘m/((?i)M<0,3>(D?C<0,3>|C[DM])(L?X<0,3>|X[LC])(I[VX]|V?I<0,3>))/g’.

Источник

netrmed

Об этом нужно знать

Как разобраться в римских цифрах?

Мы все пользуемся римскими цифрами – отмечаем ими номера веков или месяцев года. Римские цифры находятся на часовых циферблатах, в том числе на курантах Спасской башни. Мы их используем, но знаем про них не так много.

Как устроены римские цифры

Римская система счета в ее современном варианте состоит из следующих базовых знаков:

X 10

L 50

C 100

D 500

M 1000

Чтобы запомнить цифры, непривычные для нас, пользующихся арабской системой, существует несколько специальных мнемонических фраз на русском и английском языках:

Мы Dарим Сочные Lимоны, Хватит Vсем Iх

Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам

I Value Xylophones Like Cows Dig Milk

Важно, что любая цифра не должна повторять больше трех раз, таким образом, самое длинное число до тысячи – 888 = DCCCLXXXVIII (500+100+100+100+50+10+10+10+5+1+1+1).

Альтернативные варианты

Запрет на четвертое использование одной и той же цифры подряд стал появляться только в XIX веке. Поэтому в старинных текстах можно увидеть варианты IIII и VIIII вместо IV и IX, и даже IIIII или XXXXXX вместо V и LX. Остатки этого написания можно увидеть на часах, где четыре часто отмечается именно с помощью четырех единиц. В старых книгах также нередки случаи двойных вычитаний – XIIX или IIXX вместо стандартных в наши дни XVIII.

Происхождение

На данный момент не существует единой теории происхождения римских цифр. Одна из самых популярных гипотез гласит, что этрусско-римские цифры произошли от системы счета, которая использует вместо цифры штрихи-зарубки.

Именно благодаря такой записи цифр подряд мы обязаны особой системе сложения римских цифр: со временем запись числа 8 (IIIIΛIII) могла сократиться до ΛIII, что убедительно демонстрирует, каким образом римская система счета получила свою специфику. Постепенно зарубки превратились в графические символы I, V и X, и приобрели самостоятельность. Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.

Альтернативная теория принадлежит Альфреду Куперу, который предположил рассмотреть римскую систему счета с точки зрения физиологии. Купер считает, что I, II, III, IIII – это графическое представление количества пальцев правой руки, выкидываемых торговцем при назывании цены. V – это отставленный большой палец, образующий вместе с ладонью подобную букве V фигуру.

Именно поэтому римские цифры суммируют не только единицы, но и складывают их с пятерками – VI, VII и т.п. – это откинутый большой палец и другие выставленные пальцы руки. Число 10 выражали с помощью перекрещивания рук или пальцев, отсюда пошел символ X. Еще один вариант – цифру V попросту удвоили, получив X. Большие числа передавали с помощью левой ладони, которая считала десятки. Так постепенно знаки древнего пальцевого счета стали пиктограммами, которые затем начали отождествлять с буквами латинского алфавита.

Современное применение

Сегодня в России римские цифры нужны, в первую очередь, для записи номера века или тысячелетия. Римские цифры удобно ставить рядом с арабскими – если написать век римскими цифрами, а затем год – арабскими, то в глазах не будет рябить от обилия одинаковых знаков. Римские цифры имеют некоторый оттенок архаичности. С их помощью также традиционно обозначают порядковый номер монарха (Петр I), номер тома многотомного издания, иногда – главы книги. Также римские цифры используются в циферблатах часов под старину. Важные числа, такие, как год олимпиады или номер научного закона, могут также фиксироваться при помощи римских цифр: II мировая, V постулат Евклида.

В разных странах римские цифры употребляются немножко по-разному: в СССР было принято указывать с помощью них месяц года (1.XI.65). На западе римскими цифрами часто пишут номер года в титрах фильмов или на фасадах зданий.

В части Европы, в особенности в Литве, нередко можно встретить обозначение римскими цифрами дней недели (I – понедельник и так далее). В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр.

В России при письме рукой принято подчеркивать римские числа снизу и сверху одновременно. Однако часто в других странах подчеркивание сверху значило увеличение регистра числа в 1000 раз (или 10000 раз при двойном подчеркивании).

Существует распространенное заблуждение о том, что современные западные размеры одежды имеют некую связь с римскими цифрами. На самом деле обозначения XXL, S, M, L и т.п. не имеют никакой связи с ними: это аббревиатуры английских слов eXtra (очень), Small (маленький), Large (большой).

Источник

Римская нумерация: история и значение

Римская нумерация возникла, как следует из названия, в Древнем Риме. Существует семь основных символов: I, V, X, L, C, D и M. Впервые эти символы начали использовать между 900 и 800 годами до н. э.

Цифры были разработаны для использования в качестве общего метода подсчета, необходимого для развития отношений и торговли. Подсчет пальцев выходил из-под контроля, так сказать, когда при счете доходили до 10.

Значение римских цифр

Считается, что система подсчета была разработана на основе руки человека.

Одна линия, или I, символизирует одну штуку чего-либо, или, соответственно, один палец. V представлял собой пять пальцев, в частности V-образную форму, сделанную большим и указательным пальцами. X соответствовал двум рукам (соединенные в одной точке, они образуют две V).

Однако точное происхождение этих цифр римской нумерации неясно. При этом изменения в их формах с III века до нашей эры хорошо известны. Представленное выше происхождение римских цифр основано на теории истории римской нумерации немецкого ученого Теодора Моммсена (1850), получившей широкое признание. Однако изучение надписей, оставленных этрусками, которые правили Италией до латинян, показывает, что римляне приняли этрусскую численную систему, начиная с V века до нашей эры. Но есть и явное различие: этруски читали свои числа справа налево, а римляне читали их слева направо.

Римская нумерация: числа с большим значением, полученные из других символов

M = 1000. Первоначально это значение представляла греческая буква phi – Φ. Иногда оно представлялось как C, I и обратная C: CIƆ, что отдаленно похоже на М. Исследователи считают совпадением, что латинское слово mille используется для обозначения тысячи.

D = 500. Символом для этого числа первоначально был знак IƆ – половина тысячи (CIƆ).

C = 100. Первоначальным символом этого числа, вероятно, был тета (Θ), а позже стала буква C.

L = 50. Первоначально значение этого символа рассматривалось как наложенные V и I или буква psi – Ψ, сглаженная таким образом, чтобы выглядеть, как инвертированная T. Затем, в конце концов, она стала похожа на L.

Как читать числа

При нумерации римскими цифрами числа формируются путем объединения различных букв и нахождения суммы этих значений. Цифры помещаются слева направо, а порядок цифр определяет, добавляются или вычитаются значения. Если одна или несколько букв помещаются после буквы большей ценности, значит, значение добавляют. Если буква помещается перед буквой большего значения, ее значение вычитают. Например, VI = 6, поскольку V больше I. Но IV = 4, так как I меньше V.

Существует ряд других правил, связанных с римскими цифрами. Например, нельзя использовать один и тот же символ более трех раз подряд. Когда дело доходит до вычитаемых сумм, вычитаются только степени 10, такие, как I, X или C, но не V или L. Например, 95 не является VC. 95 обозначается как XCV. XC равно 100 минус 10 или 90, поэтому XC плюс V или 90 плюс 5 равно 95.

Кроме того, только одно число может быть вычтено из другого. Например, 13 не является IIXV. Легко понять, как строится ход рассуждения: 15 минус 1 минус 1. Но, следуя правилу, вместо этого пишется XIII, или 10 плюс 3.

Кроме того, нельзя вычесть число из числа, которое больше исходного более чем в 10 раз. То есть, можно вычесть 1 из 10 (IX), но нельзя вычесть 1 из 100, нет такого числа, как IC. Вместо этого следует написать XCIX (XC + IX или 90 + 9). Для больших чисел в тысячах черта, помещенная над буквой или строкой букв, умножает значение цифры на 1000.

Самые большие числа

Недостатки римской системы нумерации

Эти цифры не лишены недостатков. Например, нет символа, обозначающего ноль, также нет возможности рассчитать дроби. Это затрудняло возможность развития общепринятой сложной математической системы, затрудняло торговлю. В конечном счете римские цифры уступили место более универсальной арабской системе, где числа читаются как одно число в последовательности. Например, 435 как четыреста тридцать пять.

Использование римских цифр

Когда Римская империя рухнула тысячу лет спустя, христианство продолжало использовать систему численности этой культуры.

На сегодняшний день римская нумерация появляется в научных работах и даже в титрах фильмов. Она используется в именованиях монархов, пап, кораблей и спортивных событий, таких как Олимпиада и Суперкубок.

Латинские цифры используются в астрономии для обозначения лун и в химии для обозначения групп периодической таблицы. Их можно увидеть в оглавлениях и рукописей, поскольку римские цифры верхнего и нижнего регистров разбивают информацию на легко организованную структуру. Теория музыки также использует римские цифры в своих обозначениях.

Эти виды использования объясняются скорее эстетическими соображениями, чем функциональными целями. Визуально цифры римской нумерации передают ощущение истории и вневременности, что особенно актуально в часах.

Источник