Что обозначено s1х на рисунке
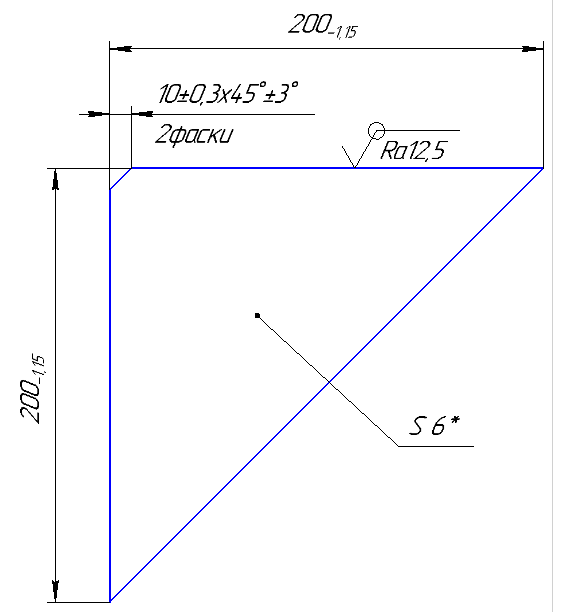
Что означает буква S на линии-выноске на чертеже, например «S4*»?
На чертежах можно встретить различные обозначения. Всем известно, что означает буквы «R», «М» и прочие на выносных линиях. А что обозначают буквой S?
Стоит заметить, что на чертежах с буквой S на линии-выноске изображается 1-2 вида. Приглядевшись, вы увидите, что не хватает размеров.
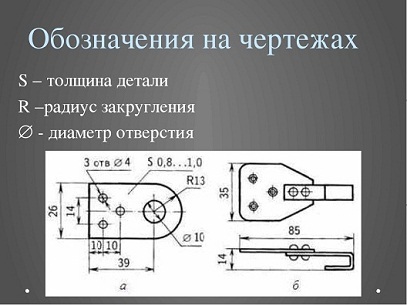
Буквой S на выносной линии обозначают толщину детали. Следующая за буквой цифра – числовое значение в миллиметрах.
Буквой «s» на линии-выноске деталировочного чертежа указывается толщина листового металла, из которого изготавливается изделие. В данном случае, обозначение S4 на линии-выноске означает, что толщина листа плоского изделия составляет 4 миллиметра.
Такой приём позволяет избежать вычерчивания лишней проекции детали.
Для удобства проектирования в программе Компас существуют привязки. В старых версиях программы меню привязок можно найти панели Текущее состояние. Оно располагается вверху окна.
В новых версиях программы (с 17) разработчики поменяли интерфейс. Теперь привязки находятся в области чертежа. Значок остался прежним – Магнит.
Для удобства можно пользоваться командой быстрого доступа. Одновременно на клавиатуре нажмите Ctrl+D. Она работает во всех версиях Компас.
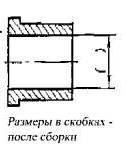
Приведу пример чертежа детали с круглыми скобками.
В круглые скобки на чертеже заключают размер детали, который должен получиться в итоге, то есть уже после сборки, соединения данной детали с другими деталями. Круглые скобки на чертеже указывают на минимальный размер детали без учета предельных отклонений и без учета припуска на механическую обработку при сборке.
В программе «Компас» нет таких спецзнаков в библиотеке. Поэтому придется действовать по старинке. Есть 2 варианта:
Как в комплекте документов отличить сборочный чертеж от монтажного?
Монтажный чертеж внешне очень похож на сборочный чертеж. Монтажные чертежи выполняются по правилам, аналогичным правилам для сборочных чертежей. Есть несколько отличий.
В монтажном чертеже помимо монтируемого изделия должны быть изображены:
Более подробную информацию можно найти в ГОСТ 2.109-73 ЕСКД.
Суть «размеров для справок», или «справочных размеров» проистекает из их названия).
Такие размеры не подлежат выполнению по рассматриваемому чертежу. Они просто указываются для большего удобства чтения и пользования чертежом, только и всего).
Обычно справочные размеры отмечаются знаком » * «. А в технических требованиях чертежа пишут:»*Размеры для справок».
Сборник тестов по инженерной графики
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Государственное бюджетное образовательное учреждение
среднего профессионального образования
«Выксунский политехнический колледж»
учебное пособие для самостоятельного контроля знаний
Преподаватель _Шаталова Н.А.
г. Выкса
Пособие предназначено для самостоятельного контроля знаний студентов всех специальностей по инженерной графике, а также в аудитории под руководством преподавателя. Этот сборник поможет облегчить и труд преподавателей, так как представляет собой дидактический материал для работы на практических занятиях.
Ключевые слова: рабочий чертеж, эскиз, сборочный чертеж, чертеж общего вида.
С помощью тестов студенты смогут проконтролировать себя, оценить реально свои знания, обнаружить слабые места в своей подготовке по инженерной графике и вовремя устранить их.
Материал располагается в соответствии с программой по инженерной графике:
.Изображения: Виды, разрезы, сечения (ГОСТ 2.305-68) 3.Нанесение размеров (ГОСТ 2.107-68)
4.Резьба и резьбовые соединения (ГОСТ 2.311-68)
Условия выполнения заданий изложены в доступной форме и направлены на выработку грамотного чтения чертежей изделий, что поможет студентам применить свои знания на практике, подготовиться к выходному контролю, а в дальнейшем выдержать контроль на остаточные знания по разделам инженерной графики.
Количество заданий в тестах по различным разделам подобрано таким образом, чтобы отразить основное содержание предмета.
Все тесты снабжены ключами-ответами.
Этот сборник поможет облегчить и труд преподавателей, так как представляет собой дидактический материал для работы на практических занятиях.
Сборник тестов предназначен как для самостоятельной работы, так и в аудитории под руководством преподавателя.
Инструкция для студентов: тест состоит из 20 вопросов. На его выполнение отводиться 15 минут. Чтобы ответить на вопросы, приведенные в таблице 1.1, нужно предварительно изучить ГОСТы 2.301-68, 2.302-68, 2.303-68, 2.304-68. Предложенные задания рекомендуется выполнять по порядку. Если студенту задание не удается выполнить самостоятельно, советуем обратиться к учебнику по инженерной графике и более внимательно прочитать содержание темы, относящейся к поставленному вопросу.
Прямоугольная система координат. Ось абсцисс и ординат
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Прямоугольная декартова система координат
Французский математик Рене Декарт преддложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.
Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.
Прямоугольная система координат в трехмерном пространстве
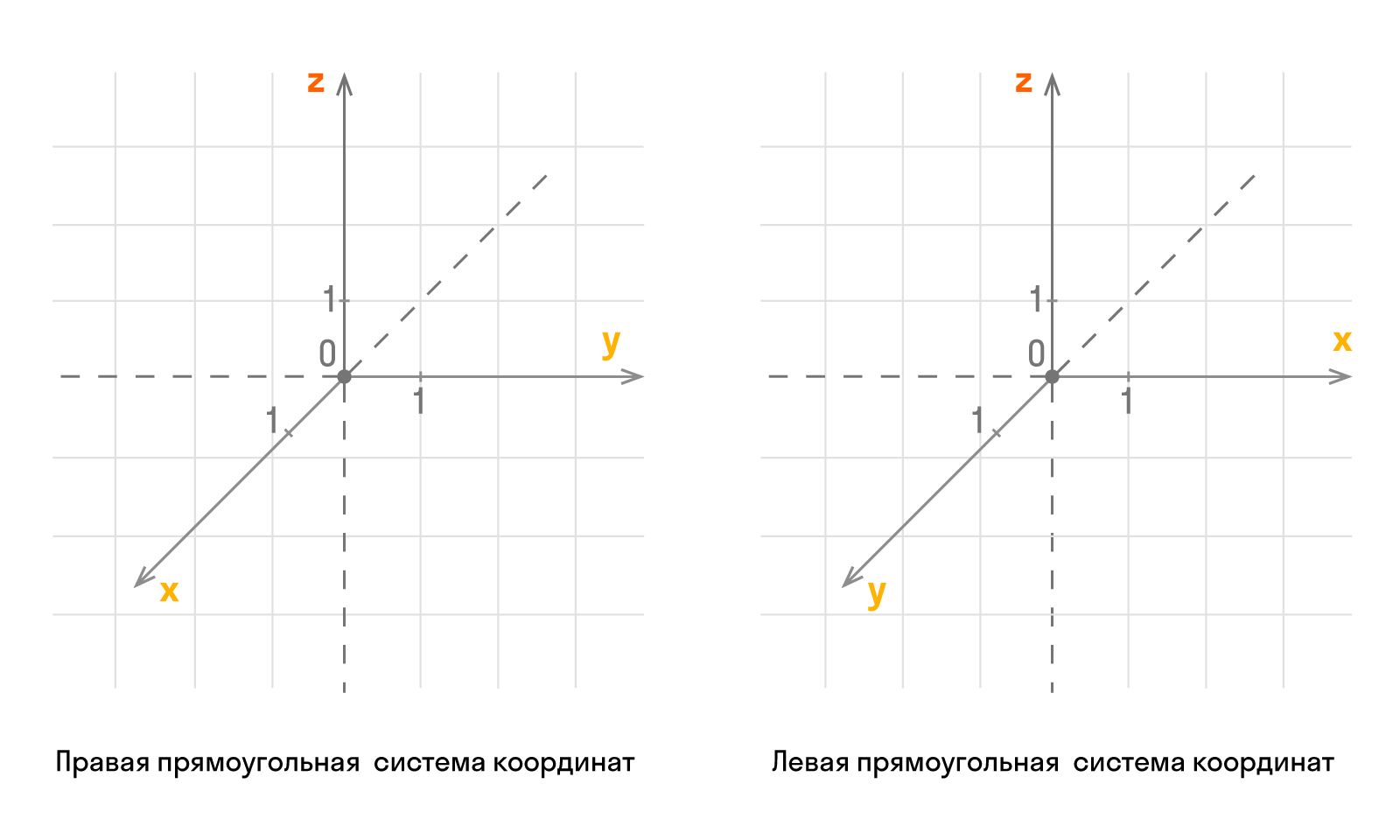
Трехмерное евклидово пространство состоит из трех взаимно перпендикулярных прямых: Ох, Оу, Оz, где Оz — ось аппликат. По направлению координатных осей есть разделение на правую и левую прямоугольные системы координат трехмерного пространства.
Оси координат пересекаются в точке О, которую называют началом. У каждой оси есть положительное направление, которое отмечается стрелкой. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Объясняем на пальцах! Если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.
Также образуется левая система координат. Совмещать обе системы нет смысла, так как соответствующие оси не совпадут.
Координаты точки в декартовой системе координат
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.
Каждая точка М, которая расположена на Ох, равна действительному числу xM. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.
Число xM — это координата точки М на заданной координатной прямой.
Пусть точка будет проекцией точки Mx на Ох, а My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения Mx и My.Тогда у точки Mx на оси Оx есть соответствующее число xM, а My на Оу — yM. Как это выглядит на координатных осях:
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса М — это xM, ордината М — это yM.
Обратное утверждение тоже верно: каждая пара (xM, yM) имеет соответствующую точку на плоскости.
Координаты точки в трехмерном пространстве
Сформулируем определение точки М в трехмерном пространстве.
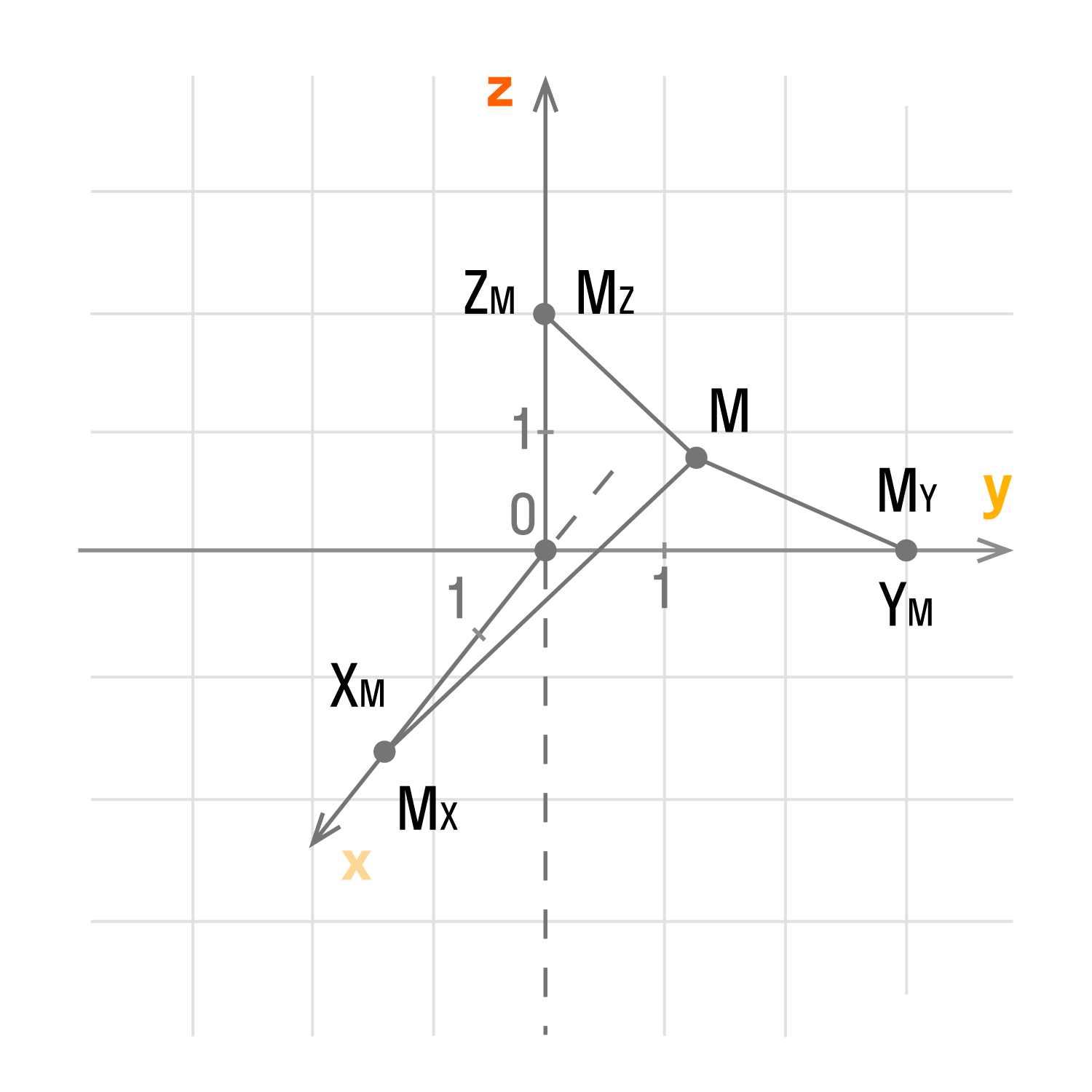
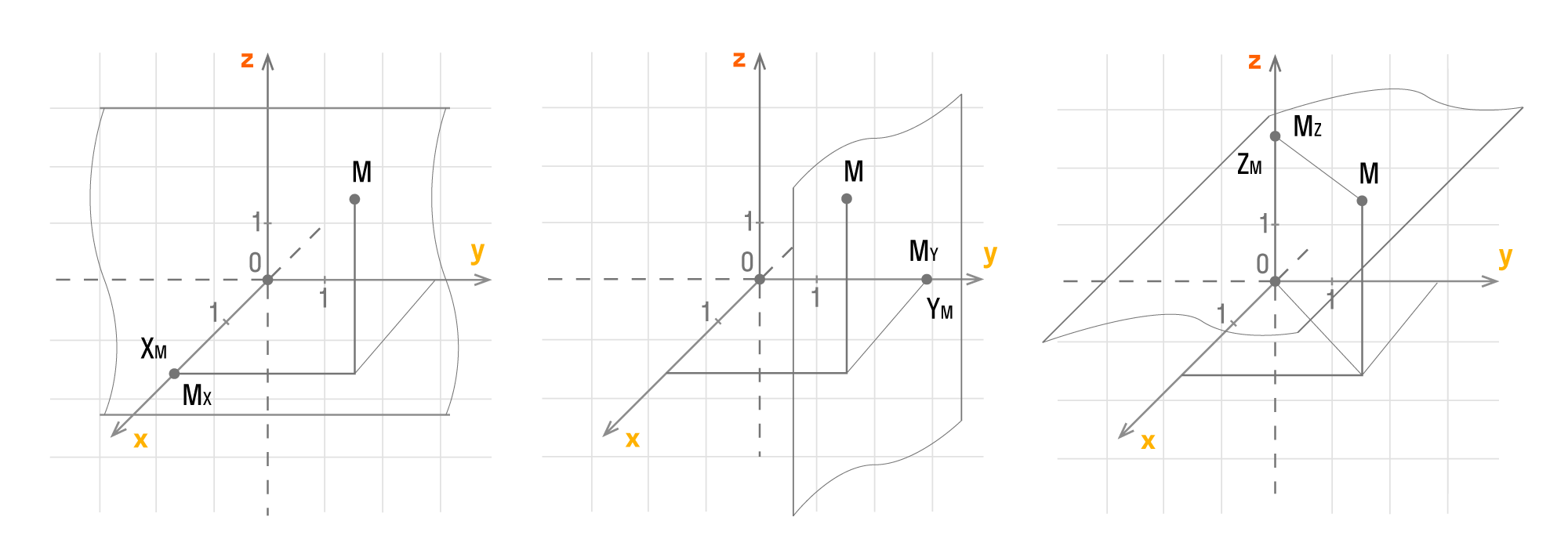
Пусть Mx, My, Mz — это проекции точки М на соответствующие оси Оx, Оy, Оz. Тогда значения этих точек на осях примут значения xM, yM, zM. Как это выглядит на координатных прямых:
Чтобы получить проекции точки М, нужно добавить перпендикулярные прямые Оx, Оy, Оz, продолжить их и изобразить в виде плоскостей, которые проходят через М. Так плоскости пересекутся в Mx, My, Mz.
У каждой точки трехмерного пространства есть свои данные (xM, yM, zM), которые являются координатами точки М.
xM, yM, zM — это числа, которые являются абсциссой, ординатой и аппликатой данной точки М. Верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (xM, yM, zM) в заданной прямоугольной системе координат имеет одну соответствующую точку М трехмерного пространства.
Что обозначено s1х на рисунке
Какими цифрами обозначены на рисунке полые вены? Какой цифрой обозначены вены, несущие артериальную кровь? Какой цифрой обозначен сосуд, в который поступает кровь из левого желудочка?
1) Верхняя и нижняя полые вены обозначены соответственно цифрами 2 и 3.
2) Легочные вены обозначены цифрой 5.
3) Аорта обозначена цифрой 1.
В ответе на второй вопрос не хватает аорты. Она тоже несет артериальную кровь.
В вопросе спрашивают: «Какой цифрой обозначены вены, несущие артериальную кровь?»
Аорта относится к артериям.
а если написать и про легочные вены и про аорту? будет считаться ошибкой? ведь спрашивали именно про вены
а что обозначено на рисунке цифрой 4?
Легочная артерия (кровь в ней венозная)
Определите, какой буквой на рисунке обозначен орган, отделяющий грудную полость от брюшной, как он называется? Какие другие функции выполняет, какой мышечной тканью образован. Чем эта ткань отличается от других мышечных тканей?
2) Диафрагма образована сухожилиями и поперечно-полосатой мышечной тканью. Другие функции: участвует в дыхании (при сокращении увеличивает объем грудной клетки), является верхней стенкой брюшной полости, с другими мышцами живота осуществляет функции брюшного пресса.
3) Поперечнополосатая мышечная ткань состоит из длинных многоядерных волокон и образует скелетные мышцы, которые работают как произвольно (по воле человека), так и рефлекторно. Волокна этой ткани способны к быстрому сокращению и долго могут находиться в сокращенном или расслабленном состоянии. Из-за чередования белков разной плотности (актина и миозина) в мышечных волокнах, данная ткань под микроскопом имеет поперечную исчерченность.