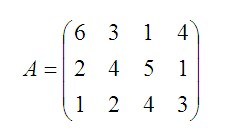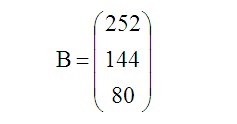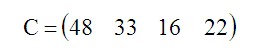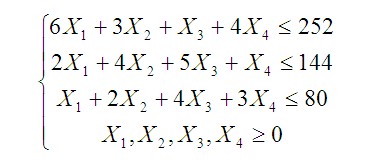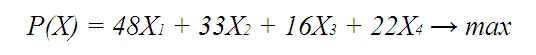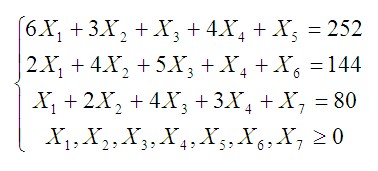Что образуют базисные столбцы в составе симплекс таблицы
Что образуют базисные столбцы в составе симплекс таблицы
Процесс нахождения экстремума с помощью симплекс-метода оформляется в виде специальных симплекс-таблиц. Симплекс-таблица составляется для каждой итерации по определенным правилам, что облегчает перебор базисных решений и позволяет избежать случайных ошибок.
Предположим, что все исходные переменные задачи x1, x2. xn – небазисные. Тогда дополнительные переменные будут базисными, и частное решение системы ограничений имеет вид
Начальная симплекс-таблица (симплекс-табл. 1) составляется на основании уравнений (2) и (4). Если перед дополнительными переменными xn+j стоит знак «+», как в (2), то все коэффициенты перед переменными xi и свободный член bj заносятся в симплекс-таблицу без изменения. Коэффициенты функции цели при ее максимизации заносятся в нижнюю строку симплекс-таблицы с противоположными знаками. Свободные члены в симплекс-таблице определяют решение задачи.
Алгоритм решения задачи следующий:
1-й шаг. Просматриваются элементы столбца свободных членов. Если все они положительные, то допустимое базисное решение найдено и следует перейти к шагу 5 алгоритма, соответствующему нахождению оптимального решения. Если в начальной симплекс-таблице есть отрицательные свободные члены, то решение не является допустимым и следует перейти к шагу 2.
2-й шаг. Для нахождения допустимого решения осуществляется пересчет симплекс-таблицы, при этом нужно решать, какую из небазисных переменных включить в базис и какую переменную вывести из базиса.
| базисные переменные | Свободные члены в ограничениях | Небазисные переменные | |||||
| x1 | x2 | . | xl | . | xn | ||
| xn+1 | b1 | a11 | a12 | . | a1l | . | a1n |
| xn+2 | b2 | a21 | a22 | . | a2l | . | a2n |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| xn+r | b2 | ar1 | ar2 | . | arl | . | arn |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| xn+m | bm | am1 | am2 | . | aml | . | amn |
| F(x)max | F0 | -c1 | -c2 | . | -c1 | . | -cn |
Для этого выбирают любой из отрицательных элементов столбца свободных членов (пусть это будет b2 ведущим, или разрешающим. Если в строке с отрицательным свободным членом нет отрицательных элементов, то система ограничений несовместна и задача не имеет решения.
Сначала в новой симплекс-таблице заполнятся строка и столбец, которые в предыдущей симплекс-таблице были ведущими. Выражение (5) означает, что элемент a’rl на месте ведущего равен обратной величине элемента предыдущей симплекс-таблицы. Элементы строки ari делятся на ведущий элемент, а элементы столбца ajl также делятся на ведущий элемент, но берутся с противоположным знаком. Элементы b’r и c’l рассчитываются по тому же принципу.
Остальные формулы легко записать с помощью правила прямоугольника.
4-й шаг. Анализ новой симплекс-таблицы начинается с 1-го шага алгоритма. Действие продолжается, пока не будет найдено допустимое базисное решение, т.е. все элементы столбца свободных членов должны быть положительными.
Рис. 1. Правило прямоугольника
6-й шаг. Рассчитываем новую симплекс-таблицу по правилам, изложенным на 3-м шаге. Процедура продолжается до тех пор, пока не будет найдено оптимальное решение или сделан вывод, что оно не существует.
Если в процессе оптимизации решения в ведущем столбце все элементы неположительные, то ведущую строку выбрать невозможно. В этом случае функция в области допустимых решений задачи не ограничена сверху и Fmax->&∞.
Если же на очередном шаге поиска экстремума одна из базисных переменных становится равной нулю, то соответствующее базисное решение называется вырожденным. При этом возникает так называемое зацикливание, характеризующееся тем, что с определенной частотой начинает повторяться одинаковая комбинация БП (значение функции F при этом сохраняется) и невозможно перейти к новому допустимому базисному решению. Зацикливание является одним из основных недостатков симплекс-метода, но встречается сравнительно редко. На практике в таких случаях обычно отказываются от ввода в базис той переменной, столбцу которой соответствует максимальное абсолютное значение отрицательного коэффициента в функции цели, и производят случайный выбор нового базисного решения.
Пример 1. Решить задачу
симплексным методом и дать геометрическую интерпретацию процесса решения.
Графическая интерпретация решения задачи представлена на рис. 2. Максимальное значение функции цели достигается в вершине ОДЗП с координатами [0,4]. Решим задачу с помощью симплекс-таблиц. Умножим второе ограничение на (-1) и введём дополнительные переменные, чтобы неравенства привести к виду равенств, тогда
Симплексный метод решения задач линейного программирования
При графическом методе решения задач ЛП мы фактически из множества вершин, принадлежащих границе множества решений системы неравенств, выбрали такую вершину, в которой значение целевой функции достигало максимума (минимума). В случае двух переменных этот метод совершенно нагляден и позволяет быстро находить решение задачи.
Если в задаче три и более переменных, а в реальных экономических задачах как раз такая ситуация, трудно представить наглядно область решений системы ограничений. Такие задачи решаются с помощью симплекс-метода или методом последовательных улучшений. Идея метода проста и заключается в следующем.
Рассмотрим симплексный метод на конкретном примере задачи о составлении плана.
Еще раз заметим, что симплекс-метод применим для решения канонических задач ЛП, приведенных к специальному виду, т. е. имеющих базис, положительные правые части и целевую функцию, выраженную через небазисные переменные. Если задача не приведена к специальному виду, то нужны дополнительные шаги, о которых мы поговорим позже.
Рассмотрим задачу о плане производства, предварительно построив модель и приведя ее к специальному виду.
Эта задача имеет специальный вид (с базисом, правые части неотрицательны). Ее можно решить симплекс-методом.
II этап. Проверка опорного плана на оптимальность.
Данной таблице 3.4 соответствует следующий опорный план:
Возможны различные ситуации.
1. В индексной F-строке нет отрицательных элементов. Значит, план оптимален, можно выписать решение задачи. Целевая функция достигла своего оптимального значения, равного числу, стоящему в правом нижнем углу, взятому с противоположным знаком. Переходим к IV этапу.
2. В индексной строке есть хотя бы один отрицательный элемент, в столбце которого нет положительных. Тогда делаем вывод о том, что целевая функция F→∞ неограниченно убывает.
3. В индексной строке есть отрицательный элемент, в столбце которого есть хотя бы один положительный. Тогда переходим к следующему III этапу. пересчитываем таблицу, улучшая опорный план.
III этап. Улучшение опорного плана.
Из отрицательных элементов индексной F-строки выберем наибольший по модулю, назовем соответствующий ему столбец разрешающим и пометим «↑».
Чтобы выбрать разрешающую строку, необходимо вычислить отношения элементов столбца свободных членов только к положительным элементам разрешающего столбца. Выбрать из полученных отношений минимальное. Соответствующий элемент, на котором достигается минимум, называется разрешающим. Будем выделять его квадратом.
Выбрав разрешающий элемент, делаем перечет таблицы по правилам:
1. В новой таблице таких же размеров, что и ранее, переменные разрешающей строки и столбца меняются местами, что соответствует переходу к новому базису. В нашем примере: х1 входит в базис, вместо х5, которая выходит из базиса и теперь свободная (табл. 3.6).
2. На месте разрешающего элемента 2 записываем обратное ему число ½.
3. Элементы разрешающей строки делим на разрешающий элемент.
4. Элементы разрешающего столбца делим на разрешающий элемент и записываем с противоположным знаком.
5. Чтобы заполнить оставшиеся элементы таблицы 3.6, осуществляем пересчет по правилу прямоугольника. Пусть мы хотим посчитать элемент, стоящий на месте 50.
Соединяем этот элемент мысленно с разрешающим, находим произведение, вычитаем произведение элементов, находящихся на другой диагонали получившегося прямоугольника. Разность делим на разрешающий элемент.
Итак, 




После пересчета таблицы убеждаемся, что в индексной строке нет отрицательных элементов, следовательно, задача решена, базисный план оптимален.
IVэтап. Выписывание оптимального решения.
— необходимо в план выпуска включить 20 изделий типа А, 40 изделий типа В, при этом прибыль будет максимальной и будет равна 220 руб.
В конце этого параграфа приведем блок-схему алгоритма симплекс-метода, которая в точности повторяет этапы, но, возможно, для некоторых читателей будет более удобна в пользовании, т. к. стрелочки указывают четкую направленность действий.
Ссылки над прямоугольниками в блок-схеме показывают, к какому этапу или подпункту относится соответствующая группа преобразований. правило нахождения первоначального опорного плана будет сформулировано в пункте 3.7.
Условно стандартная задача линейного программирования
Решение производственной задачи табличным симплекс-методом
Рассмотрим алгоритм табличного симплекс-метода на примере решения производственной задачи, которая сводится к нахождению производственного плана обеспечивающего максимальную прибыль.
Решение задачи табличным симплекс-методом
Решение задачи происходит в несколько последовательных этапов. Разберем их на небольшом примере производственной задачи.
1. Определение исходных данных
В нашем примере, по условиям задачи предприятие выпускает 4 вида изделий, обрабатывая их на 3 станках.
Исходные данные для производственной задачи запишем в формате матриц :
Таким образом, нормы времени (мин./шт.) на обработку изделий на станках, заданы матрицей A:
Фонд времени работы станков (мин.) задан в матрице B:
Прибыль от продажи каждой единицы изделия (руб./шт.) задана матрицей C:
Кроме того, обозначим через Xi планируемое количество изделий каждого вида. Тогда искомый план: X1, X2, X3, X4.
2. Запись ограничений плана в виде системы неравенств
Запишем ограничения плана в виде системы неравенств:
Коэффициенты при переменных в левой части системы неравенств берем из матрицы A, значения из правой части — из матрицы B.
Неравенства задают для каждого станка ограничение на суммарное время обработки им всех видов изделий, которое не должно превышать соответствующий ему фонд времени (т. к. станок чисто физически не может проработать ни минутой больше).
Также добавляем условие, согласно которому переменные не могут быть меньше нуля, так как произвести отрицательное количество изделий невозможно.
3. Определение целевого показателя
В нашей задаче целевой показатель — прибыль, которую следует максимизировать путем составления оптимального плана производства.
Тогда целевая прибыль может быть записана через следующее равенство:
Коэффициенты при переменных берем из матрицы C. То есть мы перемножаем прибыль от производства единицы изделия каждого вида на их планируемое количество, для получения значения суммарной прибыли (которая должна быть максимальной).
4. Приведение системы неравенств к системе линейных уравнений
Для решения получившейся задачи на условный экстремум, заменим систему неравенств системой линейных уравнений путем ввода в нее дополнительных неотрицательных переменных (X5, X6, X7).
Эти переменные являются фиктивными изделиями, на которые мы списываем неиспользованные остатки фондов времени работы станков.
5. Формирование опорного плана
Примем следующий опорный план (предварительный вариант, который в процессе решения задачи будет итерационно улучшаться):
Здесь основным переменным (количеству изделий производимых в рамках плана) сопоставляем нулевые значения, а дополнительным (фиктивным) переменным — соответствующие величины фондов времени работы станков.
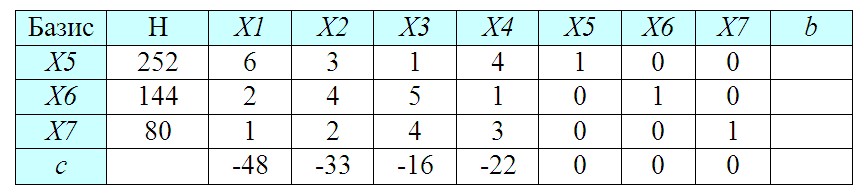
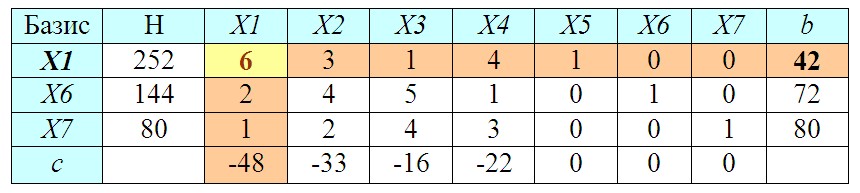
6. Составление симплекс-таблицы
Занесем исходные данные в специальную симплекс-таблицу.
В столбец Базис выписываем дополнительные переменные (X5..X7). В колонку H вносим величины фонда времени работы станков. В столбцы X1..X7 помещаем коэффициенты при этих переменных из составленной ранее системы уравнений (если переменных в уравнении нет, как например, X6 и X7 в первом равенстве, то коэффициенты будут равны 0). Кроме того, следует предусмотреть дополнительный столбец (b) для показателя, который мы будем рассчитывать на следующем этапе.
Количество строк в таблице соответствует числу дополнительных переменных (X5..X7). В последнюю строку (c) заносим коэффициенты при целевой функции с обратным знаком (коэффициенты при дополнительных переменных X5..X7 будут нулевыми).
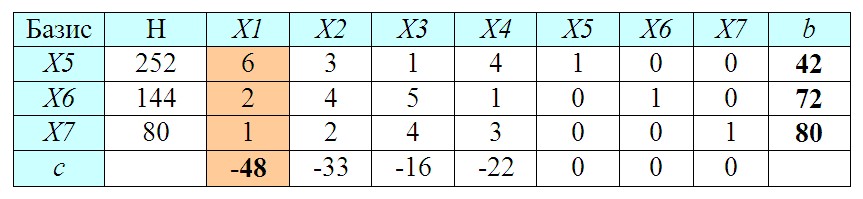
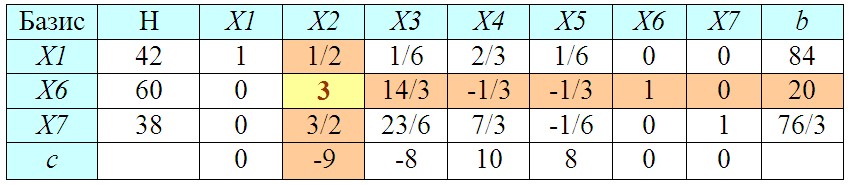
7. Вычисление показателя b
Выбираем в последней строке наибольшее (по модулю!) отрицательное число.
Далее вычислим для столбца, которому соответствует выбранное число, специальный показатель bi = Нi / ai, где ai — значение ячейки выбранного столбца и соответствующей строки.
8. Нахождение разрешающего элемента
Среди вычисленных значений b выбираем наименьшее.
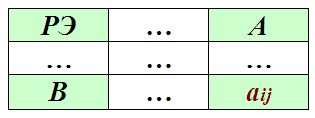
Пересечение выбранных столбца и строки даст нам разрешающий элемент (РЭ). Меняем базисную переменную (из первой колонки в выбранной строке) на переменную соответствующую разрешающему элементу (X5 на X1).
9. Перерасчет элементов симплекс-таблицы
Теперь необходимо пересчитать все элементы симплекс-таблицы, кроме столбца b (который очищается).
При перерасчете элементов симплекс-таблицы следует придерживаться следующих правил:
Формула здесь следующая: aij * = aij — ( A × B / РЭ )
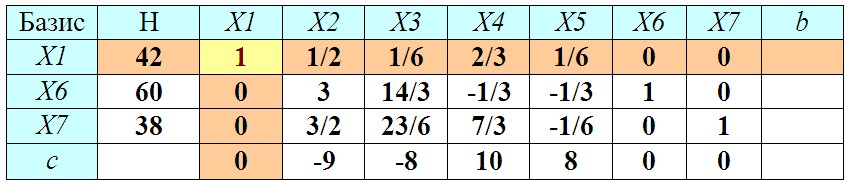
Полученные в результате перерасчета значения заносим в новую симплекс-таблицу:
10. Проверяем последнюю строку симплекс-таблицы на наличие отрицательных чисел: если их нет — оптимальный план найден (п. 11), если есть — план требует улучшения (п. 7)
Вновь проверяем последнюю строку (c) на наличие отрицательных чисел. Если их нет — оптимальный план найден, переходим к последнему этапу решения задачи (пункт 11). Если есть — план еще не оптимален, и симплекс-таблицу вновь нужно пересчитать.
Так как у нас в последней строке снова имеются отрицательные числа, начинаем новую итерацию (повторение) вычислений с пункта 7.
В нашем примере мы снова ищем в последней строке наибольшее по модулю отрицательное число, вычисляем для соответствующего ему столбца показатель b, определяем разрешающий элемент, меняем базис и пересчитываем элементы симплекс-таблицы.
Пересчитав таблицу мы видим, что на сей раз в последней строке нет отрицательных чисел, следовательно оптимальный план (позволяющий получить максимальную прибыль) найден и можно переходить к завершающему пункту решения.
Еще раз обращаю ваше внимание, что отсутствие в последней строке отрицательных элементов указывает на то, что нами найден оптимальный план производства позволяющий получить максимально возможную прибыль при заданных условиях.
11. Определение производственного плана и вычисление общей прибыли
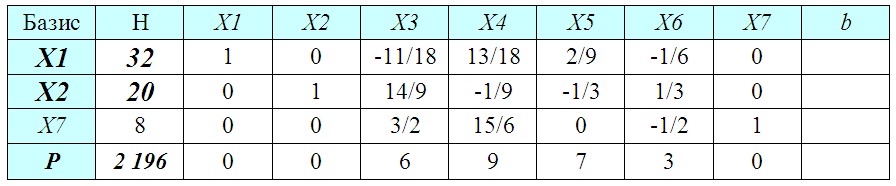
В соответствии с найденным планом (смотрим какие переменные перешли в колонку «Базис») выпускать мы будем изделия X1 и X2 (X7 не учитываем, т. к. это фиктивное изделие, не производимое на предприятии и введенное для приведения системы неравенств к системе уравнений).
Прибыль от производства каждой единицы продукции нам известна (матрица C). Остается перемножить ее с найденными объемами выпуска изделий X1 и X2 (значения X3 и X4 нулевые, т. к. эти изделия производить оказалось невыгодно), для получения общей (максимально возможной!) прибыли.
Ответ План производства: X1 = 32 шт., X2 = 20 шт., X3 = 0 шт., X4 = 0 шт., общая прибыль: P = 48 × 32 + 33 × 20 = 2 196 руб.
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Подробный разбор симплекс-метода
Пролог
Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.
Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.
§1. Постановка задачи линейного программирования
Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.
Общая задача линейного программирования (далее – ЛП) имеет вид:
§2. Каноническая форма задачи ЛП
Каноническая форма задачи ЛП:
Замечание: Любая задача ЛП сводится к канонической.
Алгоритм перехода от произвольной задачи ЛП к канонической форме:
Замечание: ≥0.
§3. Угловые точки. Базисные/свободные переменные. Базисные решения
Определение: Точка называется угловой точкой, если представление
возможно только при
.
Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е.
– не внутренняя точка).
Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.
Определение: Пусть есть система m уравнений и n неизвестных (m