Что общего у арифметической средней и гармонической средней
Гармоническое Среднее
Что такое Гармоническое Среднее?
Гармоническое среднее – это разновидность среднего численного значения. Он рассчитывается путем деления количества наблюдений на обратную величину каждого числа в серии. Таким образом, гармоническое среднее является величиной, обратной среднему арифметическому обратных величин.
Среднее гармоническое значение 1, 4 и 4 равно:
Краткая справка
Обратное значение числа n равно 1 / n.
Основы гармонического среднего
Гармоническое среднее помогает найти мультипликативные отношения или отношения делителей между дробями, не беспокоясь об общих знаменателях. Гармонические средние часто используются для усреднения таких вещей, как скорости (например, средняя скорость движения при продолжительности нескольких поездок).
Средневзвешенное гармоническое среднее используется в финансах для усреднения мультипликаторов, таких как соотношение цены и прибыли, поскольку оно придает одинаковый вес каждой точке данных. Использование взвешенного среднего арифметического для усреднения этих соотношений даст больший вес высоким точкам данных, чем низким точкам данных, потому что соотношение цена / прибыль не нормализуется по цене, в то время как прибыль выравнивается.
Ключевые моменты
Сравнение среднего гармонического и среднего арифметического и среднего геометрического
Другие способы вычисления средних значений включают простое среднее арифметическое и среднее геометрическое. Среднее арифметическое – это сумма серии чисел, деленная на количество этой серии чисел. Если бы вас попросили найти среднее (арифметическое) среднее количество баллов за тест, вы просто сложите все баллы учащихся, а затем разделите эту сумму на количество учащихся. Например, если пять студентов сдали экзамен и их баллы составили 60%, 70%, 80%, 90% и 100%, средняя арифметическая оценка по классу будет 80%.
Среднее геометрическое среднее из набора продуктов, расчет которых обычно используется для определения результатов эффективности инвестиций или портфеля. Технически это определяется как «произведение корня n-й степени из n чисел». Среднее геометрическое должно использоваться при работе с процентами, которые выводятся из значений, в то время как стандартное среднее арифметическое работает с самими значениями.
Гармоническое среднее лучше всего использовать для таких дробей, как ставки или кратные.
Пример среднего гармонического
В качестве примера возьмем две фирмы. Один имеет рыночную капитализацию 100 миллиардов долларов и прибыль 4 миллиарда долларов (P / E 25), а другой – рыночную капитализацию 1 миллиард долларов и прибыль 4 миллиона долларов (P / E 250). В индексе, составленном из двух акций, с 10% инвестиций в первую и 90% во вторую, коэффициент P / E индекса равен:
Средняя арифметическая и средняя гармоническая величины



Сущность и значение средних величин, их виды
Наиболее распространенной формой статистического показателя является средняя величина. Показатель в форме средней величины выражает типичный уровень признака в совокупности. Широкое применение средних величин объясняется тем, что они позволяют и сравнивать значения признака у единиц, относящихся к разным совокупностям. Например, можно сравнивать среднюю продолжительность рабочего дня, средний тарифный разряд рабочих, средний уровень заработной платы по различным предприятиям.
Сущность средних величин заключается в том, что в них взаимопогашаются отклонения значений признака у отдельных единиц совокупности, обусловленные действием случайных факторов. Поэтому средние величины должны рассчитываться для достаточно многочисленных совокупностей (в соответствии с законом больших чисел). Надежность средних величин зависит также от колеблемости значений признака в совокупности. В общем случае, чем меньше вариация признака и чем больше совокупность, по которой определяется средняя величина, тем она надежнее.
Типичность средней величины непосредственным образом связана также с однородностью статистической совокупности. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. В противном случае метод средних используется в сочетании с методом группировок. Если совокупность неоднородна, то общие средние заменяются или дополняются групповыми средними, рассчитанными по качественно однородным группам.
Выбор вида средних определяется экономическим содержание ем исследуемого показателя и исходных данных. Наиболее часто в статистике применяются следующие виды средних величин: степенные средние (арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т. д.), средняя хронологическая, а также структурные средние (мода и медиана).
Средняя арифметическая величина наиболее часто встречается в социально-экономических исследованиях. Средняя арифметическая применяется в форме простой средней и взвешенной средней.
Средняя арифметическая простая рассчитывается по несгруппированным данным на основании формулы (4.1):
где x— индивидуальные значения признака (варианты);
n— число единиц совокупности.
Пример. Требуется найти среднюю выработку рабочего в бригаде, состоящей из 15 человек, если известно количество изделий, произведенных одним рабочим (шт.): 21; 20; 20; 19; 21; 19; 18; 22; 19; 20; 21; 20; 18; 19; 20.
Средняя арифметическая простая рассчитывается по несгруппированным данным на основании формулы (4.2):
∑f — общее число единиц совокупности (∑f = n).
Пример. На основании имеющихся данных о распределении рабочих бригады по количеству выработанных ими изделий требуется найти среднюю выработку рабочего в бригаде.
| Выработка деталей одним рабочим, шт., x | Число рабочих, чел., f | xf |
| ВСЕГО |
Примечание 1. Средняя величина признака в совокупности может рассчитываться как на основании индивидуальных значений признака, так и на основании групповых (частных) средних, рассчитанных по отдельным частям совокупности. При этом используется формула средней арифметической взвешенной, а в качестве вариантов значений признака рассматриваются групповые (частные) средние (xj).
Пример. Имеются данные о среднем стаже рабочих по цехам завода. Требуется определить средний стаж рабочих в целом по заводу.
| Номер цеха | Средний стаж работы, лет., X | Число рабочих, чел., f |
| ВСЕГО | — |
Пример. Имеются данные о распределении рабочих предприятия по уровню заработной платы.
| Группы рабочих по заработной плате, тыс.руб. | Число рабочих, чел., f | Средняя заработная плата, тыс.руб. x ’ | x ’ f |
| До 250 250-350 350-450 450-550 550-650 650 и более | |||
| ВСЕГО | — |
Средняя гармоническая величина является модификацией средней арифметической. Применяется в тех случаях, когда известны индивидуальные значения признака, т. е. варианты (x), и произведений вариант на частоту (xf = М), но неизвестны сами частоты (f).
Средняя гармоническая взвешенная рассчитывается по формуле (4.3):
Пример. Требуется определить средний размер заработной платы работников объединения, состоящего из трех предприятий, если известен фонд заработной платы и средняя заработная плата работников по каждому предприятию.
| Предприятие | Фонд заработной платы, тыс. руб., xf | Средняя заработная плата, тыс. руб., x |
| 40 700 | ||
| 38 700 | ||
| 50 700 | ||
| ВСЕГО | — |
Средняя гармоническая простая в практике статистики используется крайне редко. В тех случаях, когда xf = Mm = const, средняя гармоническая взвешенная превращается в среднюю гармоническую простую (4.4):
Другие виды степенных средних. Средняя хронологическая
Средняя геометрическая величина используется при расчете средних показателей динамики. Средняя геометрическая применяется в форме простой средней (для несгруппированных данных) и взвешенной средней (для сгруппированных данных).
Средняя геометрическая простая (4.5):
где n — число значений признака;
П — знак произведения.
Средняя геометрическая взвешенная (4.6):
Средняя квадратическая величина используется при расчете показателей вариации. Применяется в форме простой и взвешенной.
Средняя квадратическая простая (4.7):
Средняя квадратическая взвешенная (4.8):
Средняя кубическая величина используется при расчете показателей асимметрии и эксцесса. Применяется в форме простой взвешенной.
Средняя кубическая простая (4.9):
Средняя кубическая взвешенная (4.10) :
Средняя хронологическая величина используется для расчета среднего уровня ряда динамики (4.11):
Структурные средние
Помимо рассмотренных выше средних величин в статистике используются структурные средние, к которым относятся мода и медиана.
Модой (Мо) называется значение изучаемого признака (вариант), которое чаще всего встречается в совокупности. В дискретном ряду мода определяется достаточно просто — по максимальному показателю частоты. В интервальном вариационном ряду мода приблизительно соответствует центру модального интервала, т. е. интервала, имеющего большую частоту (частость).
Конкретное значение моды рассчитывается по формуле (4.12):
где 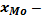
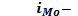
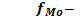
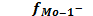
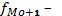
Для ранжированного ряда с нечетным числом членов медианой является варианта, расположенная в центре ряда. Положение медианы определяется порядковым номером единицы ряда в соответствии с формулой (4.13):
Для ранжированного ряда с четным числом членов медианой является среднее арифметическое из двух смежных значений, находящихся в центре ряда.
В интервальном вариационном ряду для нахождения медианы применяется следующая формула (4.14):
где 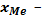
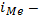
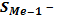
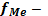
Пример. Рабочие бригады, состоящей из 9 чел., имеют следующие тарифные разряды: 4; 3; 4; 5; 3; 3; 6; 2;6. Требуется определить модальное и медианное значения тарифного разряда.
Поскольку в данной бригаде больше всего рабочих 3-го разряда, то этот разряд и будет модальным, т. е. Мо = 3.
Для определения медианы осуществим ранжирование исходного ряда в порядке возрастания значений признака:
Центральным в этом ряду является пятое по счету значение признака. Соответственно Ме = 4.
Пример. Требуется определить модальный и медианный тарифный разряд рабочих завода по данным следующего ряда распределения.
| Разряд | Кол-во рабочих, чел. | Накопленная частота S |
| 13+25=38 38+30=68 68+19=87 87+10=97 97+3=100 | ||
| ВСЕГО |
Поскольку исходный ряд распределения является дискретным, то модальное значение определяется по максимальному показателю частоты. В данномпримере на заводе больше всего рабочих 3-го разряда (fmax = 30), т.е. этот разряд является модальным (Мо = 3).
Определим положение медианы. Исходный ряд распределения построен на основании ранжированного ряда, упорядоченного по возрастанию значений признака. Середина ряда находится между 50-м и 51-м порядковыми номерами значений признака. Выясним, к какой группе относятся рабочие с этими порядковыми номерами. Для этого рассчитаем накопленные частоты. Накопленные частоты указывают на то, что медианное значение тарифного разряда равно трем (Ме = 3), поскольку значения признака с порядковыми номерами от 39-го до 68-го, в том числе 50-е и 51-е, равны 3.
Пример. Требуется определить модальную и медианную заработную плату рабочих завода по данным следующего ряда распределения.
| Размер заработной платы, тыс.руб. | Кол-во рабочих, чел. | Накопленная частота S |
| 1 | 2 | 3 |
| 180-240 240-300 300-360 360-420 420-480 480-540 540-600 | 5 15 20 30 15 10 5 | 5 20 40 70 85 95 100 |
| ВСЕГО | 100 | 100 |
Поскольку исходный ряд распределения является интервальным, то модальное значение заработной платы рассчитывается по формуле. При этом модальным является интервал 360-420 с максимальной частотой, равной 30.
Медианное значение заработной платы также рассчитывается по формуле. При этом медианным является интервал 360-420, накопленная частота которого равна 70, тогда как накопленная частота предыдущего интервала составляла только 40 при общем числе единиц, равном 100.
Средние величины и показатели вариации
Понятие и виды средних величин
Существует 2 класса средних величин: степенные и структурные.
К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.
Степенные средние величины
Степенные средние могут быть простыми и взвешенными.
Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле:
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:
Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида, которые будут далее подробно рассмотрены.
Средняя арифметическая
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической простой: (3+4+4+5)/4 = 16/4 = 4.
Средняя арифметическая взвешенная имеет следующий вид:
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической взвешенной: (3*1 + 4*2 + 5*1)/4 = 16/4 = 4.
Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X отсутствует нижняя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X.
Средняя арифметическая применяется чаще всего, но бывают случаи, когда необходимо применение других видов средних величин. Рассмотрим такие случаи далее.
Средняя гармоническая
Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:
Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:
Средняя геометрическая
Средняя геометрическая применяется при определении средних относительных изменений, о чем сказано в теме Ряды динамики. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.
Средняя квадратическая
Средняя квадратическая применяется в тех случая, когда исходные значения X могут быть как положительными, так и отрицательными, например при расчете средних отклонений.
Главной сферой применения квадратической средней является измерение вариации значений X, о чем пойдет речь позднее в этой лекции.
Средняя кубическая
Средняя кубическая применяется крайне редко, например, при расчете индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН.
Структурные средние величины
К наиболее часто используемым структурным средним относятся статистическая мода и статистическая медиана.
Статистическая мода
Если X задан дискретно, то мода определяется без вычисления как значение признака с наибольшей частотой. В статистической совокупности бывает 2 и более моды, тогда она считается бимодальной (если моды две) или мультимодальной (если мод более двух), и это свидетельствует о неоднородности совокупности.
Если X задан равными интервалами, то сначала определяется модальный интервал как интервал с наибольшей частотой f. Внутри этого интервала находят условное значение моды по формуле:
где Мо – мода;
ХНМо – нижняя граница модального интервала;
hМо – размах модального интервала (разность между его верхней и нижней границей);
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующего модальному;
fМо+1 – частота интервала, следующего за модальным.
Если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.
Статистическая медиана
Если X задан дискретно, то для определения медианы все значения нумеруются от 0 до N в порядке возрастания, тогда медиана при четном числе N будет лежать посередине между X c номерами 0,5N и (0,5N+1), а при нечетном числе N будет соответствовать значению X с номером 0,5(N+1).
Если X задан в виде равных интервалов, то сначала определяется медианный интервал (интервал, в котором заканчивается одна половина частот f и начинается другая половина), в котором находят условное значение медианы по формуле:
где Ме – медиана;
ХНМе – нижняя граница медианного интервала;
hМе – размах медианного интервала (разность между его верхней и нижней границей);
fМе – частота медианного интервала; 
Также как и в случае с модой, при определении медианы если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.
Показатели вариации
Размах вариации
Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:
Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.
Cреднее линейное отклонение
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4. Рассчитаем среднее линейное отклонение простое: Л = (|3-4|+|4-4|+|4-4|+|5-4|)/4 = 0,5.
Вернемся к примеру про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4 и среднее линейное отклонение простое = 0,5. Рассчитаем среднее линейное отклонение взвешенное: Л = (|3-4|*1+|4-4|*2+|5-4|*1)/4 = 0,5.
Линейный коэффициент вариации
С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.
В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, линейный коэффициент вариации составит 0,5/4 = 0,125 или 12,5%.
Дисперсия
В уже знакомом нам примере про студента, который сдал 4 экзамена и получил оценки: 3, 4, 4 и 5, ранее уже была рассчитана средняя арифметическая = 4. Тогда дисперсия простая Д = ((3-4) 2 +(4-4) 2 +(4-4) 2 +(5-4) 2 )/4 = 0,5.
В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию взвешенную: Д = ((3-4) 2 *1+(4-4) 2 *2+(5-4) 2 *1)/4 = 0,5.
Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то можно получить еще одну формулу для ее расчета как разность средней квадратов и квадрата средней:
В уже знакомом нам примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию методом разности средней квадратов и квадрата средней:
Д = (3 2 *1+4 2 *2+5 2 *1)/4-4 2 = 16,5-16 = 0,5.

Cреднее квадратическое отклонение
Выше уже было рассказано о формуле средней квадратической, которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:
Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:
В примере про студента, в котором выше рассчитали дисперсию, найдем среднее квадратическое отклонение как корень квадратный из нее:
.
Квадратический коэффициент вариации
В примере про студента, в котором выше рассчитали среднее квадратическое отклонение, найдем квадратический коэффициент вариации V = 0,707/4 = 0,177, что меньше критериального значения 0,333, значит вариация слабая и равна 17,7%.



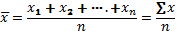
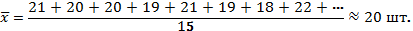
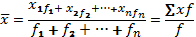
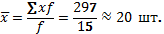
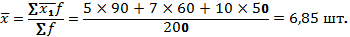

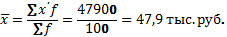
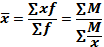
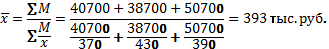
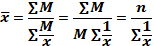
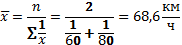
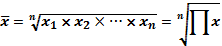
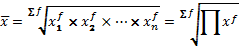
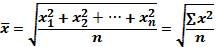
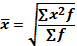
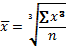
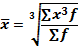
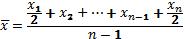
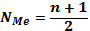
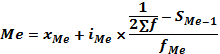
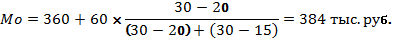




















 .
.