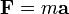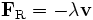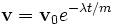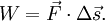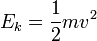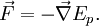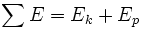Что объясняет механика ньютона
Ньютоновская механика
| Фундаментальные понятия |
|---|
| Пространство · Время · Масса · Сила Энергия · Импульс |
| Формулировки |
|---|
| Ньютоновская механика Лагранжева механика Гамильтонова механика |
| Разделы |
|---|
| Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика |
| Учёные |
|---|
| Галилей · Кеплер · Ньютон Эйлер · Лаплас · Д’Аламбер Лагранж · Гамильтон · Коши |
Класси́ческая меха́ника — вид механики (раздела физики, изучающей законы изменения положений тел и причины, это вызывающие), основанный на 3 законах Ньютона и принципе относительности Галилея. Поэтому её часто называют «Ньютоновской механикой». Важное место в классической механике занимает существование инерциальных систем. Классическая механика подразделяется на кинематику (которая изучает геометрическое свойство движения без рассмотрения его причин), статику (которая рассматривает равновесие тел) и динамику (которая рассматривает движение тел).
Классическая механика дает очень точные результаты в рамках повседневного опыта. Но для систем, движущихся с большими скоростями, приближающимися к скорости света, более точные результаты дает релятивистская механика, для систем микроскопических размеров — квантовая механика, а для систем, обладающих обеими характеристиками — квантовая теория поля. Тем не менее, классическая механика сохраняет свое значение, поскольку (1) она намного проще в понимании и использовании, чем остальные теории, и (2) в обширном диапазоне она достаточно хорошо приближается к реальности. Классическую механику можно использовать для описания движения таких объектов, как волчок и бейсбольный мяч, многих астрономических объектов (таких, как планеты и галактики), и даже многих микроскопических объектов, таких как органические молекулы.
Хотя классическая механика в общих чертах совместима с другими «классическими теориями», такими как классическая электродинамика и термодинамика, в конце 19 века были найдены несоответствия, которые удалось разрешить только в рамках более современных физических теорий. В частности, классическая электродинамика предсказывает, что скорость света постоянна для всех наблюдателей, что трудно совместить с классической механикой, и что привело к необходимости создания специальной теории относительности. При рассмотрении совместно с классической термодинамикой, классическая механика приводит к парадоксу Гиббса в котором невозможно точно определить величину энтропии и к ультрафиолетовой катастрофе, в которой абсолютно чёрное тело должно излучать бесконечное количество энергии. Попытки разрешить эти проблемы привели к развитию квантовой механики.
Содержание
Описание теории
Перейдем к изложению основных понятий классической механики. Для простоты, мы будем рассматривать только материальную точку, т. е. тело, размером которого можно пренебречь. Движение материальной точки характеризуется несколькими параметрами: её положением, массой, и приложенными к ней силами. Рассмотрим каждый из них по очереди.
В действительности, любое тело, которое подчиняется законам классической механики, обязательно имеет ненулевой размер. Настоящие материальные точки, такие, как электрон, подчиняются законам квантовой механики. Тела ненулевого размера могут испытывать более сложные движения, поскольку может меняться их внутренняя конфигурация, например, потому что теннисный мяч может двигаться, вращаясь. Тем не менее, мы сможем применить к подобным телам результаты, полученные для материальных точек, рассматривая такие тела, как совокупности большого количества взаимодействующих материальных точек. Мы сможем показать, что такие сложные тела ведут себя, как материальные точки, при условии, что они малы в масштабах рассматриваемой задачи.
Радиус-вектор и его производные
Радиус-вектор материальной точки указывает на её положение по отношению к произвольной точке, зафиксированной в пространстве, которая обычно называется началом координат, и обозначается O. Это вектор r соединяющий начало координат с частицей. В общем случае, материальная точка движется, поэтому r является функцией t, промежутка времени прошедшего с произвольного начального момента. Скорость изменения положения со временем, определяется так:
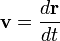
Ускорение, или скорость изменения скорости, это:
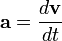
Вектор ускорения может меняться за счет изменения его направления, величины, или и того и другого. Если скорость уменьшается, иногда пользуются термином «замедление», но вообще, термин «ускорение» относится к любому изменению скорости.
Второй закон Ньютона
Второй закон Ньютона связывает массу и скорость частицы с векторной величиной, известной как сила. Пусть m — масса тела и F — векторная сумма всех приложенных к нему сил (то есть равнодействующая сила.) Тогда второй закон Ньютона выглядит так:
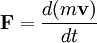
Величина mv называется импульсом. В большинстве случаев, масса m не изменяется со временем, и закон Ньютона можно записать в упрощенной форме
где a — ускорение, определенное выше. Не всегда выполняется условие независимости массы от времени. Например, масса ракеты уменьшается по мере использования горючего. В таких случаях последнее выражение неприменимо, и следует пользоваться полной формой второго закона Ньютона.
Второго закона Ньютона недостаточно для описания движения частицы. Дополнительно требуется описание силы F, полученное из рассмотрения сущности физического взаимодействия, в котором участвует тело. Например, сила трения может быть смоделирована как функция скорости частицы, а именно
где λ — некоторая положительная постоянная. Получив независимое выражение для каждой силы, действующей на тело, мы можем подставить его во второй закон Ньютона и получим дифференциальное уравнение, называемое уравнением движения. Продолжая наш пример, примем, что на тело действует только сила трения. Тогда уравнение движения будет иметь вид
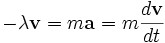
Это можно интегрировать, что даст
где v0 — начальная скорость. Это означает, что скорость тела экспоненциально уменьшается со временем до нуля. Проинтегрировав последнее выражение, мы можем получить радиус-вектор r тела, как функцию времени.
Важными силами являются сила всемирного тяготения и сила Лоренца для электромагнетизма. Помимо этого, для определения сил, действующих на тело, используется третий закон Ньютона: если мы знаем, что тело A действует с силой F на тело B, значит B должно действовать с равной по величине и противоположной по направлению силой реакции, −F, на A.
Энергия
Если сила 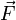
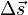
Если масса частицы постоянна, а Wtotal полная работа, совершенная частицей, определяемая как сумма работ совершенных приложенными к частице силами, то второй закон Ньютона примет вид:
где Ek называется кинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до скорости v :
Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.
Если все силы, действующие на частицу консервативны, и Ep является полной потенциальной энергий, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:
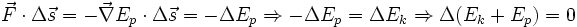 . . |
Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы
является постоянной относительно времени. Это очень полезно, потому что часто приходится сталкиваться с консервативными силами.
Механика Ньютона
Формирование классической механики и основанной на ней механистической картины мира происходило по двум направлениям:
· обобщение полученных ранее результатов и прежде всего законов свободно падающих тел, открытых Галилеем, а также законов движения планет, сформулированных Кеплером;
· создание методов для количественного анализа механического движения в целом.
Великий английский ученый Исаак Ньютон (1643–1727) создал свой вариант дифференциального и интегрального исчисления непосредственно для решения основных проблем механики: определения мгновенной скорости как производной от пути по времени движения, и – ускорения как производной от скорости по времени. Благодаря этому ему удалось сформулировать основные законы динамики и закон всемирного тяготения. Теперь количественный подход к описанию движения кажется чем-то само собой разумеющимся, но в XVII в. это было крупнейшим завоеванием научной мысли.
Механика Ньютона–законченная система классической механики, основанная на понятиях количества материи (массы тела), количества движения, силы и трех законах движения: закона инерции, закона пропорциональности силы и ускорения и закона равенства действия и противодействия – изложена в знаменитом труде Ньютона «Математические начала натуральной философии» (1687). В своей механике Ньютон отказался от построения всеобъемлющей картины Вселенной и создал свой метод физического исследования, опирающийся на опыт, ограничивающийся фактами и не претендующий на познание конечных причин. Основной задачей механики Ньютона является нахождение движения по силам, или, наоборот, нахождение действующих сил по движениям без анализа природы взаимодействия.
Классическая механика Ньютона сыграла и играет до сих пор огромную роль в развитии естествознания. Она объясняет множество физических явлений и процессов в земных и в неземных условиях, составляет основу для многих технических достижений. На ее фундаменте базируются многие методы научных исследований в различных отраслях естествознания.
В основе классической механики лежит концепция Ньютона, определившая лицо естествознания вплоть до ХХ в. Согласно ньютоновской концепции, физическая реальность характеризуется понятиями пространства, времени, материальной точки и силы (взаимодействия материальных точек). В ньютоновской концепции под физическими событиями следует понимать движение материальных точек в пространстве, управляемое неизменными законами. Материальную точку мыслят как аналогию подвижных тел, лишенных таких признаков, как протяженность, форма, ориентация в пространстве, и всех «внутренних» свойств, за исключением только инерции и перемещения. Материальные тела, которые психологически привели к образованию понятия «материальной точки», сами рассматриваются как системы материальных точек.
В 1667 г. Ньютон сформулировал три закона динамики, составляющие основной раздел классической механики и являющиеся, как и большинство физических законов, обобщением результатов огромного человеческого опыта. Законы Ньютона рассматривают обычно как систему взаимосвязанных законов.
Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние.
Стремление тела сохранить состояние покоя или равномерного прямолинейного движения называется инертностью, или инерцией. Поэтому первый закон Ньютона называют также законом инерции.
Для количественной формулировки второго закона динамики вводятся понятия ускорения а, массы тела m и силы F. Ускорением характеризуется быстрота изменения скорости движения тела. Масса тела – физическая величина, одна из основных характеристик материи, определяющая ее инерционные свойства (инертная масса) и гравитационные свойства (тяжелая или гравитационная масса). Сила F – это векторная величина, мера механического воздействии на тело со стороны других тел или полей, в результате которого тело приобретает ускорение, или изменяет свою форму и размеры.
Второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе и обратно пропорционально массе материальной точки (тела)
Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго. Действительно, в случае равенства нулю равнодействующих сил (при отсутствии воздействия на тело со стороны других тел) ускорение также равно нулю. Однако первый закон Ньютона рассматривается как самостоятельный закон, а не как следствие второго закона, так как именно он утверждает существование инерциальных систем отсчета.
Взаимодействие между материальными точками (телами) определяется третьим законом динамики– законом равенства действия и противодействия.
Третий закон Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:
где F12 – сила, действующая на первую материальную точку со стороны второй; F21 – сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы. Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек, характеризующихся парным взаимодействием.
Одним из достижений механики Ньютона является закон всемирного тяготения, открытый в 1665–1666 гг. и выражающий общее свойство всех тел притягивать друг друга с силой, пропорциональной произведению масс тел m1, m2 и обратно пропорциональной квадрату расстояния R между ними:
где g – гравитационная постоянная.
Законы Ньютона позволяют решить многие задачи механики – от простых до сложных. Спектр таких задач значительно расширился после разработки Ньютоном и Лейбницем нового для того времени математического аппарата – дифференциального и интегрального исчисления, весьма эффективного при решении многих динамических задач и особенно задач небесной механики.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Законы механики Ньютона
В отсутствие внешних силовых воздействий тело будет продолжать равномерно двигаться по прямой.
Ускорение движущегося тела пропорционально сумме приложенных к нему сил и обратно пропорционально его массе.
Всякому действию сопоставлено равное по силе и обратное по направлению противодействие.
Законы Ньютона — в зависимости от того, под каким углом на них посмотреть, — представляют собой либо конец начала, либо начало конца классической механики. В любом случае это поворотный момент в истории физической науки — блестящая компиляция всех накопленных к тому историческому моменту знаний о движении физических тел в рамках физической теории, которую теперь принято именовать классической механикой. Можно сказать, что с законов движения Ньютона пошел отсчет истории современной физики и вообще естественных наук.
Однако Исаак Ньютон взял названные в его честь законы не из воздуха. Они, фактически, стали кульминацией долгого исторического процесса формулирования принципов классической механики. Мыслители и математики — упомянем лишь Галилея (см. Уравнения равноускоренного движения) — веками пытались вывести формулы для описания законов движения материальных тел — и постоянно спотыкались о то, что лично я сам для себя называю непроговоренными условностями, а именно — обе основополагающие идеи о том, на каких принципах зиждется материальный мир, которые настолько устойчиво вошли в сознание людей, что кажутся неоспоримыми. Например, древним философам даже в голову не приходило, что небесные тела могут двигаться по орбитам, отличающимся от круговых; в лучшем случае возникала идея, что планеты и звезды обращаются вокруг Земли по концентрическим (то есть вложенным друг в друга) сферическим орбитам. Почему? Да потому, что еще со времен античных мыслителей Древней Греции никому не приходило в голову, что планеты могут отклоняться от совершенства, воплощением которой и является строгая геометрическая окружность. Нужно было обладать гением Иоганна Кеплера, чтобы честно взглянуть на эту проблему под другим углом, проанализировать данные реальных наблюдений и вывести из них, что в действительности планеты обращаются вокруг Солнца по эллиптическим траекториям (см. Законы Кеплера).
Первый закон Ньютона
Учитывая столь серьезный, исторически сложившийся провал, первый закон Ньютона сформулирован безоговорочно революционным образом. Он утверждает, что если какую-либо материальную частицу или тело попросту не трогать, оно будет продолжать прямолинейно двигаться с неизменной скоростью само по себе. Если тело равномерно двигалось по прямой, оно так и будет двигаться по прямой с неизменной скоростью. Если тело покоилось, оно так и будет покоиться, пока к нему не приложат внешних сил. Чтобы просто сдвинуть физическое тело с места, к нему нужно обязательно приложить стороннюю силу. Возьмем самолет: он ни за что не стронется с места, пока не будут запущены двигатели. Казалось бы, наблюдение самоочевидное, однако, стоит нам отвлечься от прямолинейного движения, как оно перестает казаться таковым. При инерционном движении тела по замкнутой циклической траектории его анализ с позиции первого закона Ньютона только и позволяет точно определить его характеристики.
Представьте себе что-то типа легкоатлетического молота — ядро на конце струны, раскручиваемое вами вокруг вашей головы. Ядро в этом случае движется не по прямой, а по окружности — значит, согласно первому закону Ньютона, его что-то удерживает; это «что-то» — и есть центростремительная сила, которую вы прилагаете к ядру, раскручивая его. Реально вы и сами можете ее ощутить — рукоять легкоатлетического молота ощутимо давит вам на ладони. Если же вы разожмете руку и выпустите молот, он — в отсутствие внешних сил — незамедлительно отправится в путь по прямой. Точнее будет сказать, что так молот поведет себя в идеальных условиях (например, в открытом космосе), поскольку под воздействием силы гравитационного притяжения Земли он будет лететь строго по прямой лишь в тот момент, когда вы его отпустили, а в дальнейшем траектория полета будет всё больше отклоняться в направлении земной поверхности. Если же вы попробуете действительно выпустить молот, выяснится, что отпущенный с круговой орбиты молот отправится в путь строго по прямой, являющейся касательной (перпендикулярной к радиусу окружности, по которой его раскручивали) с линейной скоростью, равной скорости его обращения по «орбите».
Теперь заменим ядро легкоатлетического молота планетой, молотобойца — Солнцем, а струну — силой гравитационного притяжения: вот вам и ньютоновская модель Солнечной системы.
Такой анализ происходящего при обращении одного тела вокруг другого по круговой орбите на первый взгляд кажется чем-то само собой разумеющимся, но не стоит забывать, что он вобрал в себя целый ряд умозаключений лучших представителей научной мысли предшествующего поколения (достаточно вспомнить Галилео Галилея). Проблема тут в том, что при движении по стационарной круговой орбите небесное (и любое иное) тело выглядит весьма безмятежно и представляется пребывающим в состоянии устойчивого динамического и кинематического равновесия. Однако, если разобраться, сохраняется только модуль (абсолютная величина) линейной скорости такого тела, в то время как ее направление постоянно меняется под воздействием силы гравитационного притяжения. Это и значит, что небесное тело движется равноускоренно. Кстати, сам Ньютон называл ускорение «изменением движения».
Первый закон Ньютона играет и еще одну важную роль с точки зрения нашего естествоиспытательского отношения к природе материального мира. Он подсказывает нам, что любое изменение в характере движения тела свидетельствует о присутствии внешних сил, воздействующих на него. Условно говоря, если мы наблюдаем, как железные опилки, например, подпрыгивают и налипают на магнит, или, доставая из сушилки стиральной машины белье, выясняем, что вещи слиплись и присохли одна к другой, мы можем чувствовать себя спокойно и уверенно: эти эффекты стали следствием действия природных сил (в приведенных примерах это силы магнитного и электростатического притяжения соответственно).
Второй закон Ньютона
Если первый закон Ньютона помогает нам определить, находится ли тело под воздействием внешних сил, то второй закон описывает, что происходит с физическим телом под их воздействием. Чем больше сумма приложенных к телу внешних сил, гласит этот закон, тем большее ускорение приобретает тело. Это раз. Одновременно, чем массивнее тело, к которому приложена равная сумма внешних сил, тем меньшее ускорение оно приобретает. Это два. Интуитивно эти два факта представляются самоочевидными, а в математическом виде они записываются так:
где F — сила, m — масса, а — ускорение. Это, наверное, самое полезное и самое широко используемое в прикладных целях из всех физических уравнений. Достаточно знать величину и направление всех сил, действующих в механической системе, и массу материальных тел, из которых она состоит, и можно с исчерпывающей точностью рассчитать ее поведение во времени.
Именно второй закон Ньютона придает всей классической механике ее особую прелесть — начинает казаться, будто весь физический мир устроен, как наиточнейший хронометр, и ничто в нем не ускользнет от взгляда пытливого наблюдателя. Назовите мне пространственные координаты и скорости всех материальных точек во Вселенной, словно говорит нам Ньютон, укажите мне направление и интенсивность всех действующих в ней сил, и я предскажу вам любое ее будущее состояние. И такой взгляд на природу вещей во Вселенной бытовал вплоть до появления квантовой механики.
Третий закон Ньютона
За этот закон, скорее всего, Ньютон и снискал себе почет и уважение со стороны не только естествоиспытателей, но и ученых-гуманитариев и попросту широких масс. Его любят цитировать (по делу и без дела), проводя самые широкие параллели с тем, что мы вынуждены наблюдать в нашей обыденной жизни, и притягивают чуть ли не за уши для обоснования самых спорных положений в ходе дискуссий по любым вопросам, начиная с межличностных и заканчивая международными отношениями и глобальной политикой. Ньютон, однако, вкладывал в свой названный впоследствии третьим закон совершенно конкретный физический смысл и едва ли замышлял его в ином качестве, нежели как точное средство описания природы силовых взаимодействий. Закон этот гласит, что если тело А воздействует с некоей силой на тело В, то тело В также воздействует на тело А с равной по величине и противоположной по направлению силой. Иными словами, стоя на полу, вы воздействуете на пол с силой, пропорциональной массе вашего тела. Согласно третьему закону Ньютона пол в это же время воздействует на вас с абсолютно такой же по величине силой, но направленной не вниз, а строго вверх. Этот закон экспериментально проверить нетрудно: вы постоянно чувствуете, как земля давит на ваши подошвы.
Тут важно понимать и помнить, что речь у Ньютона идет о двух силах совершенно разной природы, причем каждая сила воздействует на «свой» объект. Когда яблоко падает с дерева, это Земля воздействует на яблоко силой своего гравитационного притяжения (вследствие чего яблоко равноускоренно устремляется к поверхности Земли), но при этом и яблоко притягивает к себе Землю с равной силой. А то, что нам кажется, что это именно яблоко падает на Землю, а не наоборот, это уже следствие второго закона Ньютона. Масса яблока по сравнению с массой Земли низка до несопоставимости, поэтому именно его ускорение заметно для глаз наблюдателя. Масса же Земли, по сравнению с массой яблока, огромна, поэтому ее ускорение практически незаметно. (В случае падения яблока центр Земли смещается вверх на расстояние менее радиуса атомного ядра.)
По совокупности же три закона Ньютона дали физикам инструменты, необходимые для начала комплексного наблюдения всех явлений, происходящих в нашей Вселенной. И, невзирая на все колоссальные подвижки в науке, произошедшие со времен Ньютона, чтобы спроектировать новый автомобиль или отправить космический корабль на Юпитер, вы воспользуетесь все теми же тремя законами Ньютона.