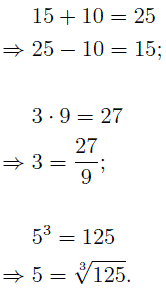Что означает арифметические действия
Основные арифметические действия: определения, примеры
В данной публикации мы рассмотрим определения, общие формулы и примеры 4 основных арифметических (математических) действий с числами: сложения, вычитания, умножения и деления.
Сложение
Сложение – это математическое действие, в результате которого находится сумма.
Обозначается сложение специальным знаком “+“ (плюс), а сумма – “Σ“.
Пример: найдем сумму чисел.
1) 3, 5 и 23.
2) 12, 25, 30, 44.
Ответы:
1) 3 + 5 + 23 = 31
2) 12 + 25 + 30 + 44 = 111.
Вычитание
Вычитание чисел – это обратное сложению математическое действие, в результате коротого находится разность ( c ). Например:
Обозначается вычитание специальным знаком “–“ (минус).
Пример: найдем разность чисел.
1) 62 минус 32 и 14.
2) 100 минус 49, 21 и 6.
Ответы:
1) 62 – 32 – 14 = 16.
2) 100 – 49 – 21 – 6 = 24.
Умножение
Умножение – это арифметическое действие, в результате которого вычисляется произведение.
Обозначается умножение специальными знаками “·“ или “x“.
Пример: найдем произведение чисел.
1) 3, 10 и 12.
2) 7, 1, 9 и 15.
Ответы:
1) 3 · 10 · 12 = 360.
2) 7 · 1 · 9 · 15 = 945.
Деление
Деление чисел – это обратное умножению действие, в результате коротого вычисляется частное ( d ). Например:
Обозначается деление специальными знаками “:“ или “/“.
Пример: найдем частное чисел.
1) 56 разделим на 8.
2) 100 разделим на 5, затем на 2.
Ответы:
1) 56 : 8 = 7.
2) 100 : 5 : 2 = 10 (, ).
Арифметика. Арифметические действия
Содержание
 Арифметика. Арифметические действия |
| Обратные арифметические действия |
| Свойства арифметических действий |
| Порядок выполнения арифметических действий |
| Умножение натуральных чисел на 10, 100, 1000; и т.д. |
Арифметика. Арифметические действия
Арифметическим действием называют операцию, удовлетворяющую ряду свойств и позволяющую по нескольким данным числам найти новое число.
Арифметикой называют науку, изучающую простейшие свойства чисел и арифметических действий.
Существуют шесть арифметических действий: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.
Обратные арифметические действия
Вычитание – это арифметическое действие, обратное к сложению, деление – действие, обратное к умножению, извлечение корня – действие, обратное к возведению в степень.
Свойства арифметических действий
Порядок выполнения арифметических действий
Сложение и вычитание называют действиями первой ступени, умножение и деление – действиями второй ступени, возведение в степень и извлечение корня – действиями третьей ступени.
Действия одной ступени выполняются в том же порядке, в каком они записаны в формуле.
Если в формуле содержатся действия разных ступеней, то сначала выполняют действия высших ступеней, а затем низших ступеней.
Если формула содержит скобки, то сначала выполняют действия в скобках. Скобки бывают круглыми, квадратными и фигурными, причем между ними нет никакой разницы.
Если скобки содержат другие скобки, то сначала выполняют действия во «внутренних» скобках.
Умножение натуральных чисел на 10, 100, 1000 и т.д.
Действительно, например, число 3610 состоит из трёх тысяч, шести сотен и одного десятка, поэтому
Порядок действий в математике
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные операции в математике
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Подставляем полученные значения в исходное выражение:
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!
Действия первой и второй ступени
Арифметические действия делятся на действия первой и второй ступени.
Порядок действий
Если выражение содержит действия только одной ступени и в нём нет скобок, то действия выполняются в порядке их следования слева направо.
Пример 1. Вычислить значение выражения:
Решение: Данное выражение содержит действия только одной ступени — первой (сложение и вычитание). Надо определить порядок действий и выполнить их.
| 1 | 2 | 3 | 4 | |||||
|---|---|---|---|---|---|---|---|---|
| 15 | + | 17 | — | 20 | + | 8 | — | 12 |
Пример 2. Вычислить значение выражения:
Решение: Данное выражение содержит действия только одной ступени — второй (умножение и деление). Надо определить порядок действий и выполнить их.
| 1 | 2 | 3 | 4 | |||||
|---|---|---|---|---|---|---|---|---|
| 60 | : | 15 | · | 7 | : | 2 | · | 3 |
Если выражение содержит действия обеих ступеней, то первыми выполняются действия второй ступени, в порядке их следования (слева направо), а затем действия первой ступени.
Пример. Вычислить значение выражения:
Решение: Данное выражение содержит четыре действия: два первой ступени и два второй. Определим порядок их выполнения: согласно правилу первым действием будет деление, вторым — умножение, третьим — сложение, а четвёртым — вычитание.
Основные арифметические действия
Сложение
Сложение – одна из основных операций, позволяющая объединить два слагаемых.
Запись сложения: 8 + 3 = 11
Вычитание
Вычитание – действие, обратное сложению.
Умножение
Умножение – арифметическое действие в виде краткой записи суммы одинаковых слагаемых.
Запись: 12 × 5 = 60 или 12 • 5 = 60
12 × 5 = 12 + 12 + 12 + 12 + 12
В случае если множимое и множитель поменять ролями, произведение остается одним и тем же. Например:
2 × 5 = 2 + 2 + 2 + 2 + 2 = 10
Поэтому и множитель, и множимое называются «сомножителями».
Деление
Деление – арифметическое действие обратное умножению.
Запись: 48 : 6 = 8 или 48 / 6 = 8
В случае, когда делимое не делится полностью, иногда применяют так называемое деление с остатком. Деление с остатком, это отыскание наибольшего подходящего целого числа, которое в произведении с делителем дает нужное число, не превышающее делимое.
Такое искомое число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком, которое всегда меньше делителя.
Возведение в степень
Возведение степень – операция умножения числа на самого себя несколько ( n ) раз.
Основание степени называется число, которое повторяется сомножителем определённое количество раз.
Показателем степени называется число, которое указывает, сколько раз берется одинаковый множитель.
Степенью называется число, получаемое в результате взаимодействия основания и показателя степени.
3 – основание степени
4 – показатель степени
Вторая степень называется иначе квадратом, третья степень – кубом. Первой степенью числа называют само это число.
Извлечение корня
Извлечение корня – арифметическое действие, обратное возведению в степень.
81 – подкоренное число
4 – показатель корня
З 4 = 81 – возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня)
2 √16 = 4 – корень второй степени называется – квадратным.
При знаке квадратного корня показатель корня принято опускать: √16 = 4
3 √8 = 2 – корень третьей степени называется – кубичным.
Сложение и вычитание, умножение и деление, а так же возведение в степень и извлечение корня попарно представляют собой обратными действиями.
Правила первых четырех действий регулирующие взаимодействия с целыми числами предполагаются известными. Возведение в степень выполняется повторным умножением.