Что означает атомистичность электрического заряда
ГЛАВА 13. ОСНОВЫ ЭЛЕКТРОСТАТИКИ
Атомистичность заряда. Закон сохранения заряда
Имеется два вида электрических зарядов, условно называемых «положительными» и «отрицательными». Заряды одного знака отталкиваются, разных знаков – притягиваются.
Электрический заряд является неотъемлемым свойством некоторых так называемых элементарных частиц. Заряд всех заряженных элементарных частиц одинаков по абсолютной величине. Его можно назвать элементарным зарядом. Обозначать его будем буквой е.
К числу элементарных частиц принадлежат – электрон (отрицательно заряжен), протон (положительно заряжен) и нейтрон (не заряжен).
Обычно частицы, несущие заряды разных знаков, присутствуют в равных количествах и распределены в теле с одинаковой плотностью. В этом случае алгебраическая сумма зарядов в любом элементарном объеме тела равна нулю, и каждый такой объем будет нейтральным.
Поскольку всякий заряд q образуется совокупностью элементарных зарядов, он является целым кратким е:
.
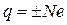
Электрические заряды могут исчезать и возникать вновь. Однако всегда возникают или исчезают одновременно два элементарных заряда противоположных знаков. Поэтому суммарный заряд электрически изолированной системы не может изменяться. Это утверждение носит название закона сохранения электрического заряда.
Электрический заряд измеряется в системе СИ в Кулонах (Кл).
Закон Кулона
В 1785 г. Кулон экспериментально, с помощью крутильных весов установил, что сила взаимодействия двух точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними
, (13.1)
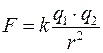
или в векторном виде
. (13.2)
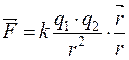
В этом выражении под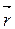 
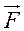
следует подразумевать вектор, проведенный от одного заряда к другому и имеющий направление к тому из зарядов, к которому приложена сила 
.
В системе СИ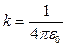 
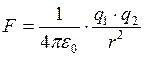
. Тогда закон Кулона примет вид
. (13.3)
Взаимодействие между зарядами осуществляется через электрическое поле. Всякий заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле. Поле проявляет себя в том, что на помещенный в какую-либо его точку электрический заряд действует сила. По величине силы можно судить об «интенсивности» поля.
Силу, действующую на единичный положительный заряд, помещенный в данную точку поля, называют напряженностью электрического поля в этой точке
. (13.4)
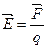
Из закона Кулона следует, что
. (13.5)
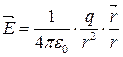
За единицу напряженности электрического поля принимается напряженность в такой же точке, в которой на заряд, равный единице действует единичная сила (в СИ 1к – заряд, 1н – сила).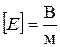 
.
Опыт показывает, что сила, с которой система зарядов действует на некоторый не входящий в систему заряд, равна векторной сумме сил, с которыми действует на данный заряд каждый из зарядов системы в отдельности. Отсюда вытекает, что напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности:
(13.6)
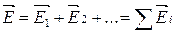
это утверждение носит название принципа суперпозиции (наложения) электрических полей.
ГЛАВА 13. ОСНОВЫ ЭЛЕКТРОСТАТИКИ
Атомистичность заряда. Закон сохранения заряда
Имеется два вида электрических зарядов, условно называемых «положительными» и «отрицательными». Заряды одного знака отталкиваются, разных знаков – притягиваются.
Электрический заряд является неотъемлемым свойством некоторых так называемых элементарных частиц. Заряд всех заряженных элементарных частиц одинаков по абсолютной величине. Его можно назвать элементарным зарядом. Обозначать его будем буквой е.
К числу элементарных частиц принадлежат – электрон (отрицательно заряжен), протон (положительно заряжен) и нейтрон (не заряжен).
Обычно частицы, несущие заряды разных знаков, присутствуют в равных количествах и распределены в теле с одинаковой плотностью. В этом случае алгебраическая сумма зарядов в любом элементарном объеме тела равна нулю, и каждый такой объем будет нейтральным.
Поскольку всякий заряд q образуется совокупностью элементарных зарядов, он является целым кратким е:
.
Электрические заряды могут исчезать и возникать вновь. Однако всегда возникают или исчезают одновременно два элементарных заряда противоположных знаков. Поэтому суммарный заряд электрически изолированной системы не может изменяться. Это утверждение носит название закона сохранения электрического заряда.
Электрический заряд измеряется в системе СИ в Кулонах (Кл).
Закон Кулона
В 1785 г. Кулон экспериментально, с помощью крутильных весов установил, что сила взаимодействия двух точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними
, (13.1)
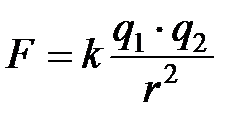
или в векторном виде
. (13.2)
В этом выражении под 
следует подразумевать вектор, проведенный от одного заряда к другому и имеющий направление к тому из зарядов, к которому приложена сила 
.
| q1 |
| q2 |
| r |
 |
В системе СИ 
. Тогда закон Кулона примет вид
. (13.3)
Взаимодействие между зарядами осуществляется через электрическое поле. Всякий заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле. Поле проявляет себя в том, что на помещенный в какую-либо его точку электрический заряд действует сила. По величине силы можно судить об «интенсивности» поля.
Силу, действующую на единичный положительный заряд, помещенный в данную точку поля, называют напряженностью электрического поля в этой точке
. (13.4)
Из закона Кулона следует, что
. (13.5)
За единицу напряженности электрического поля принимается напряженность в такой же точке, в которой на заряд, равный единице действует единичная сила (в СИ 1к – заряд, 1н – сила). 
.
Опыт показывает, что сила, с которой система зарядов действует на некоторый не входящий в систему заряд, равна векторной сумме сил, с которыми действует на данный заряд каждый из зарядов системы в отдельности. Отсюда вытекает, что напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности:
(13.6)
это утверждение носит название принципа суперпозиции (наложения) электрических полей.
Поток вектора напряженности
.
Следовательно, N численно равна
,
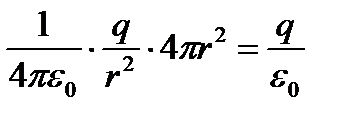
т.е. полное число линий на любом расстоянии от заряда будет одно и то же. Следовательно, линии нигде, кроме заряда, не начинаются и не заканчиваются; они, начавшись на заряде, уходят в бесконечность, либо, приходя из бесконечности, заканчиваются на заряде.
Поскольку густота линий 
выбирается равной численному значению Е, количество линий, пронизывающих площадку dS, перпендикулярных будет численно равна ЕdS. Если площадка dS ориентирована так, что нормаль к ней образует с вектором угол a, то количество линий, пронизывающих площадку, будет численно равно ЕdS cos a= En dS, где En – составляющая вектора по направлению нормали к площадке.
Отсюда для количества линий , пронизывающих произвольную поверхность, получается следующее выражение:
.
Если имеется поле некоторого вектора 
, то выражение 
, где Ап – составляющая вектора по направлению нормали к dS, называется потоком вектора через поверхность S.
Следовательно, поток вектора
(13.7)
численно равен количеству линий , пронизывающих поверхность S.
Теорема Гаусса
В предыдущем разделе было показано, что окружающую точечный заряд qсферическую поверхность любого радиуса r пересекает 
линий . Отсюда вытекает, что из точечного заряда выходит 
линий.
Поток вектора через некоторую поверхность численно равен количеству линий , пересекающих эту поверхность. Следовательно, поток вектора через охватывающую заряд сферическую поверхность равен . Знак потока совпадает со знаком заряда.
Не сферическая поверхность без «морщин» пересекается каждой линией только один раз. Поэтому число пересечений равно количеству линий, выходящих из заряда, т.е. .
| + |
| + |
| + |
| + |
| — |
Если поверхность с «морщинами», то число пересечений может быть только нечетным и потому противоположные вклады, вносимые в общий поток
Рис. 13.3. взаимно уничтожаются, за
Пусть внутри некоторой замкнутой поверхности заключено несколько точечных зарядов произвольный знаков: q1, q2 и т.д. Поток вектора по определению равен
(13.8)
(кружок у знака интеграла указывает на то, что интегрирование производится по замкнутой поверхности).
В силу принципа суперпозиции полей
.
Подставив это в выражение для потока, получим
,
где 
— нормальная составляющая напряженности поля, создаваемого і-м зарядом в отдельности.
Но 
.
Следовательно 
. (13.9)
Доказанное утверждение называется теоремой Гаусса. Эта теорема может быть сформулирована следующим образом: поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e0.
Если внутри поверхности заряды отсутствуют, поток равен нулю.
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, теорема Гаусса должна быть записана следующим образом:
, (13.10)
где интеграл справа берется по объему V, охватываемому поверхностью S.
Теорема Гаусса позволяет найти напряженность поля гораздо проще, чем с использованием формулы для напряженности поля точечного заряда и принципа суперпозиции.
Электрический заряд, атомистичность заряда, элементарный заряд
Все тела в природе способны электризоваться, т.е. приобретать электрический заряд. Причем заряды существуют двух знаков: условно называемые положительными и отрицательными.
Электрический заряд является неотъемлемым свойством некоторых элементарных частиц. Заряд всех элементарных частиц (если он не равен нулю) одинаков по абсолютной величине. Его называют элементарным зарядом. Положительный элементарный заряд обозначают +е, отрицательный – -е.
Поскольку всякий заряд q образуется совокупностью элементарных зарядов, он является целым кратным е:
(1)
Однако электрический заряд настолько мал, что возможную величину макроскопических зарядов можно считать изменяющейся непрерывно.
Если физическая величина может принимать только определённые дискретные значения, говорят, что эта величина квантуется. Факт, выражаемый формулой (1.1), означает, что электрический заряд квантуется.
Величина заряда, измеряемая в различных инерциальных системах отсчёта, оказывается одинаковой. Следовательно, электрический заряд является релятивистки инвариантным. Отсюда вытекает, что величина заряда не зависит от того, движется этот заряд или покоится.
В СИ электрический заряд измеряют в кулонах (Кл). Однако, несмотря на то, что первое понятие в электричестве, с которым мы встретились ‑ это заряд, единица измерения заряда ‑ Кулон (Кл) ‑ в СИ не является основной. Четвертой основной единицей в СИ (наряду с метром, килограммом и секундой) является единица силы тока ‑ 1 Ампер (А). При этом 1 Кл ‑ это такое количество электричества, которое протекает через поперечное сечение проводника за 1 секунду, при силе тока в 1 Ампер ‑ 
.
Сравнительно недавно была высказана гипотеза о существовании в природе частиц с зарядом, равным 1/3 элементарного, так называемых кварков. Предполагают, что из кварков состоят протоны, нейтроны и другие, относительно тяжелые частицы. Однако, обнаружить кварки экспериментально пока не удалось.
Закон сохранения заряда
Таким образом, суммарный заряд электрически изолированной системы не может изменяться. Это утверждение носит название закона сохранения электрического заряда.
Отметим, что закон сохранения электрического заряда тесно связан с релятивисткой инвариантностью заряда. Действительно, если бы величина заряда зависела от его скорости, то, приведя в движение заряды одного какого-то знака, мы изменили бы суммарный заряд изолированной системы.
Закон Кулона
Заряженные тела взаимодействуют друг с другом, причем одноименные заряды отталкиваются, а разноименные притягиваются.
Точное математическое выражение закона этого взаимодействия в 1785 г. установил французский физик Ш.Кулон. С тех пор закон взаимодействия неподвижных электрических зарядов носит его имя.
Заряженное тело, размерами которого можно пренебречь, по сравнению с расстоянием между взаимодействующими телами может быть принято за точечный заряд. Кулон в результате своих опытов установил, что:
Сила взаимодействия в вакууме двух неподвижных точечных зарядов прямо пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними. Индекс « 
» у силы показывает, что это сила взаимодействия зарядов в вакууме.
Установлено, что закон Кулона справедлив на расстояниях от 
до нескольких километров.
Чтобы поставить знак равенства, необходимо ввести некоторый коэффициент пропорциональности, величина которого зависит от выбора системы единиц:
Уже отмечалось, что в СИ заряд измеряется в Кл. В законе Кулона известна размерность левой части ‑ единица силы 
, известна размерность правой части ‑ 
, поэтому коэффициент k получается размерным и равным 
. Однако в СИ этот коэффициент пропорциональности принято записывать в несколько другом виде:
, (2)
следовательно 
или 
,
Величину 
называют электрической постоянной. Это действительно фундаментальная постоянная, фигурирующая во многих уравнениях электродинамики.
Таким образом, закон Кулона в скалярной форме имеет вид:
.
Закон Кулона может быть выражен в векторной форме:
, (3)
Опыт показывает, что сила взаимодействия двух данных зарядов не изменяется, если вблизи них расположить ещё какие-либо другие заряды.
Электростатическое поле
Взаимодействие между покоящимися зарядами осуществляется через промежуточную среду и с конечной скоростью.
Впервые такая идея была высказана М.Фарадеем. Согласно его представлениям заряды не действуют друг на друга непосредственно. Каждый из них создает в окружающем пространстве электрическое поле. Поле одного заряда действует на другой и наоборот. Причем поле заряда не действует на сам заряд.
Если мы изменим положение заряда в пространстве, либо изменим его величину, то поле этого заряда также изменится. Причем изменение поля на некотором расстоянии произойдет не мгновенно c изменением положения заряда или его величины, а спустя некоторый промежуток времени. Таким образом, электрическое поле изменяется не мгновенно, а с конечной скоростью.
Эта скорость называется скоростью распространения электромагнитного взаимодействия, равна скорости света в пустоте и имеет численное значение 
.
Электростатическое поле – это материальная среда, т. к. взаимодействие между телами (зарядами) может передаваться только через материю. Будучи материальной средой, поле обладает свойствами, присущими материи, а именно – массой, энергией и др.
Поле проявляет себя в том, что помещенный в какую-либо его точку электрический заряд оказывается под действием силы. Следовательно, для того чтобы выяснить, имеется ли в данном месте электрическое поле, надо поместить туда заряженное тело («пробный» заряд).
Введем понятие напряжённости поля. Если в поле, создаваемое зарядом 
, поместить пробный точечный заряд 
, то на него действует сила 
, различная в разных точках поля, которая, согласно закону Кулона (3), пропорциональна пробному заряду . Поэтому отношение 
не зависит от и характеризует электростатическое поле в той точке, где пробный заряд находится.
Эта векторная величина называется напряженностью поля 
и является силовой характеристикой электростатического поля. Чем больше напряженность поля, тем с большей силой оно действует на заряд.
В общем случае вектор 
определяется по формуле:
,
а в случае поля точечного заряда
(4)
Напряженность поля ‑ это физическая величина, равная отношению силы, действующей на пробный точечный заряд в данной точке поля к величине этого заряда.
Направлен вектор вдоль радиальной прямой, проходящей через заряд q и данную точку поля A, от заряда, если он положителен, и к заряду, если он отрицателен (рис. 2)
За единицу напряженности электрического поля принимают напряженность такого поля, в котором на заряд в 1 Кл действует сила в 1Н. В СИ эта единица называется «Ньютон на Кулон»: 
, где вольт (В) – единица потенциала электростатического поля.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.