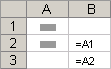
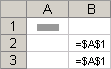
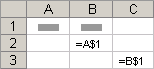
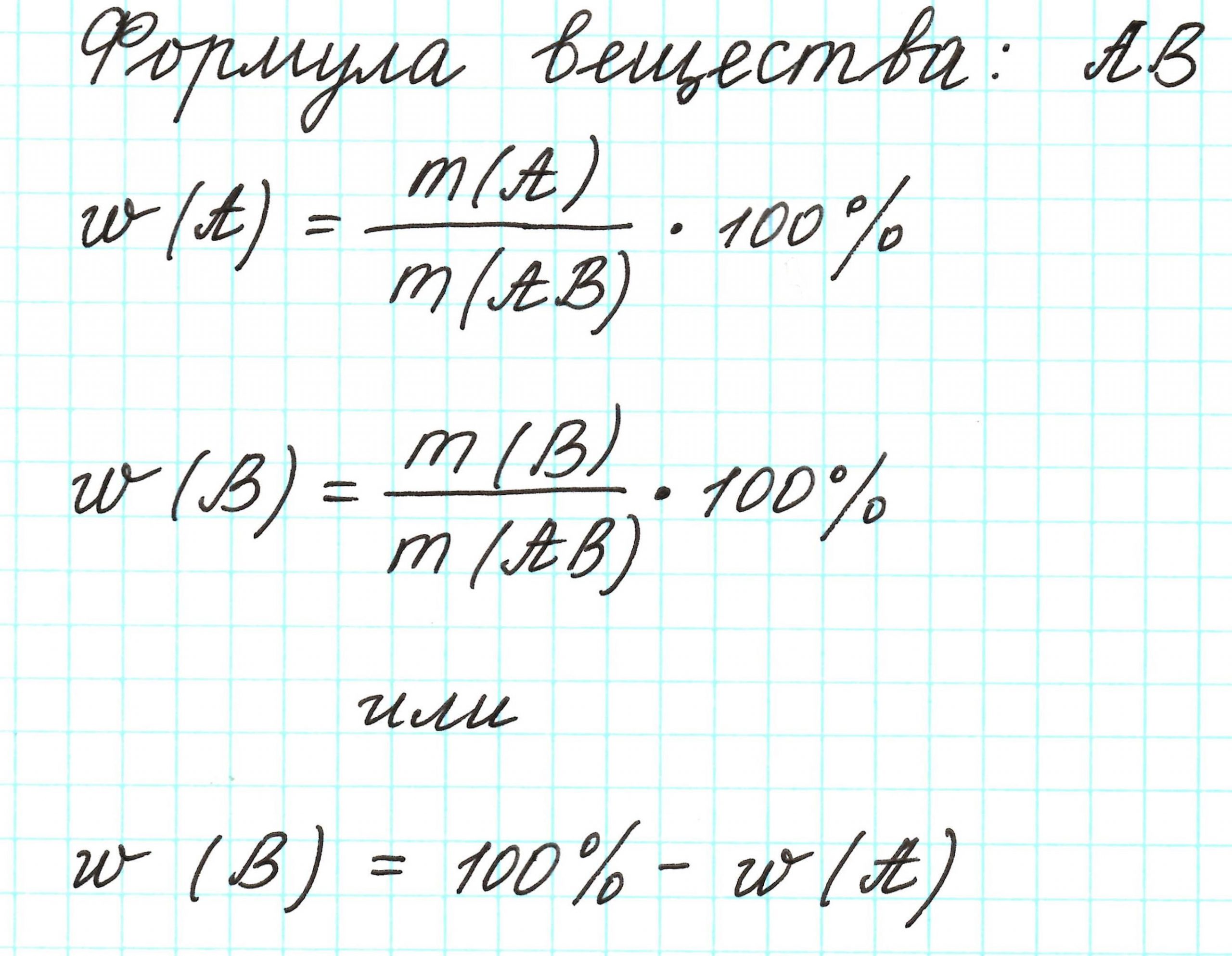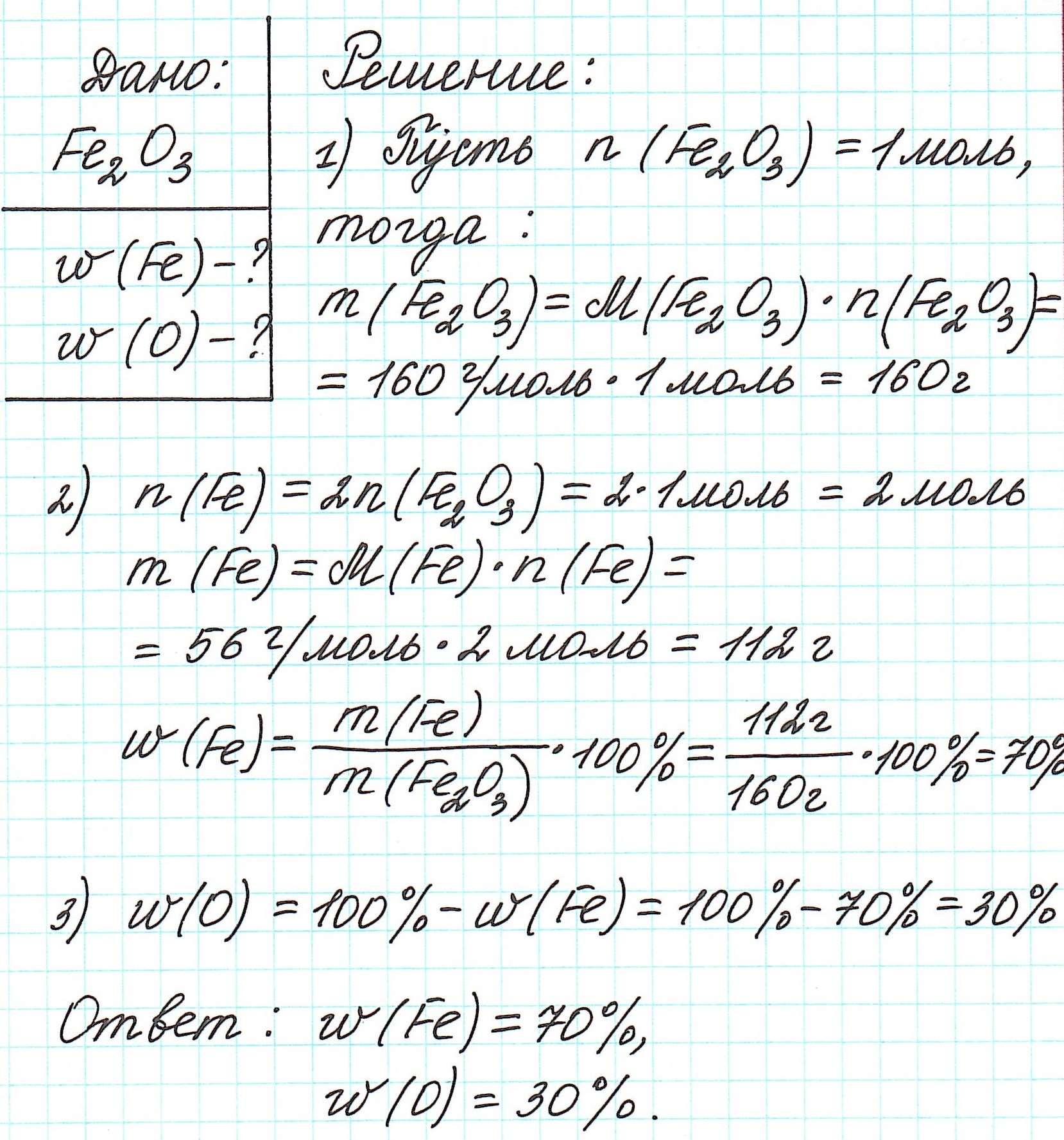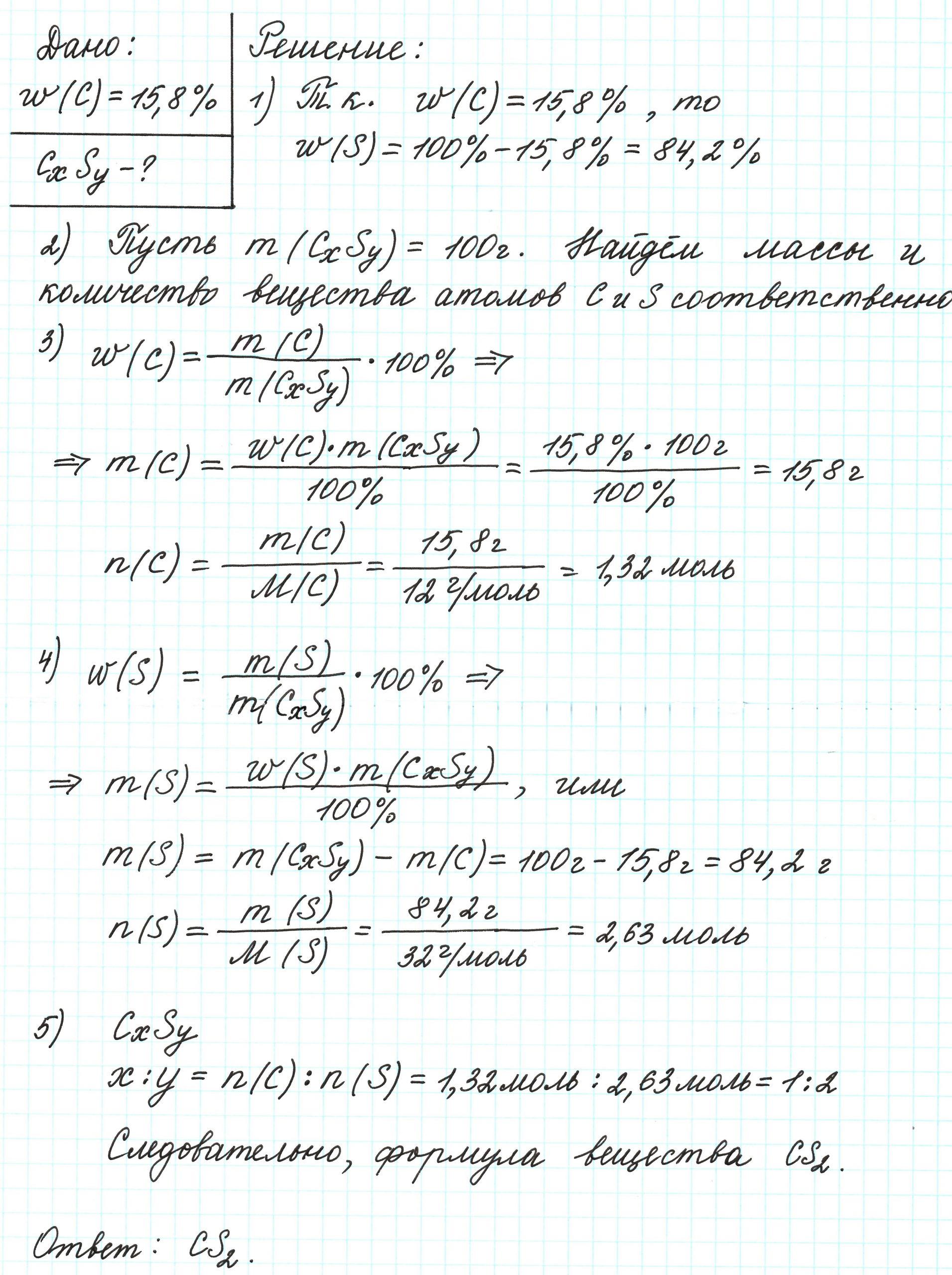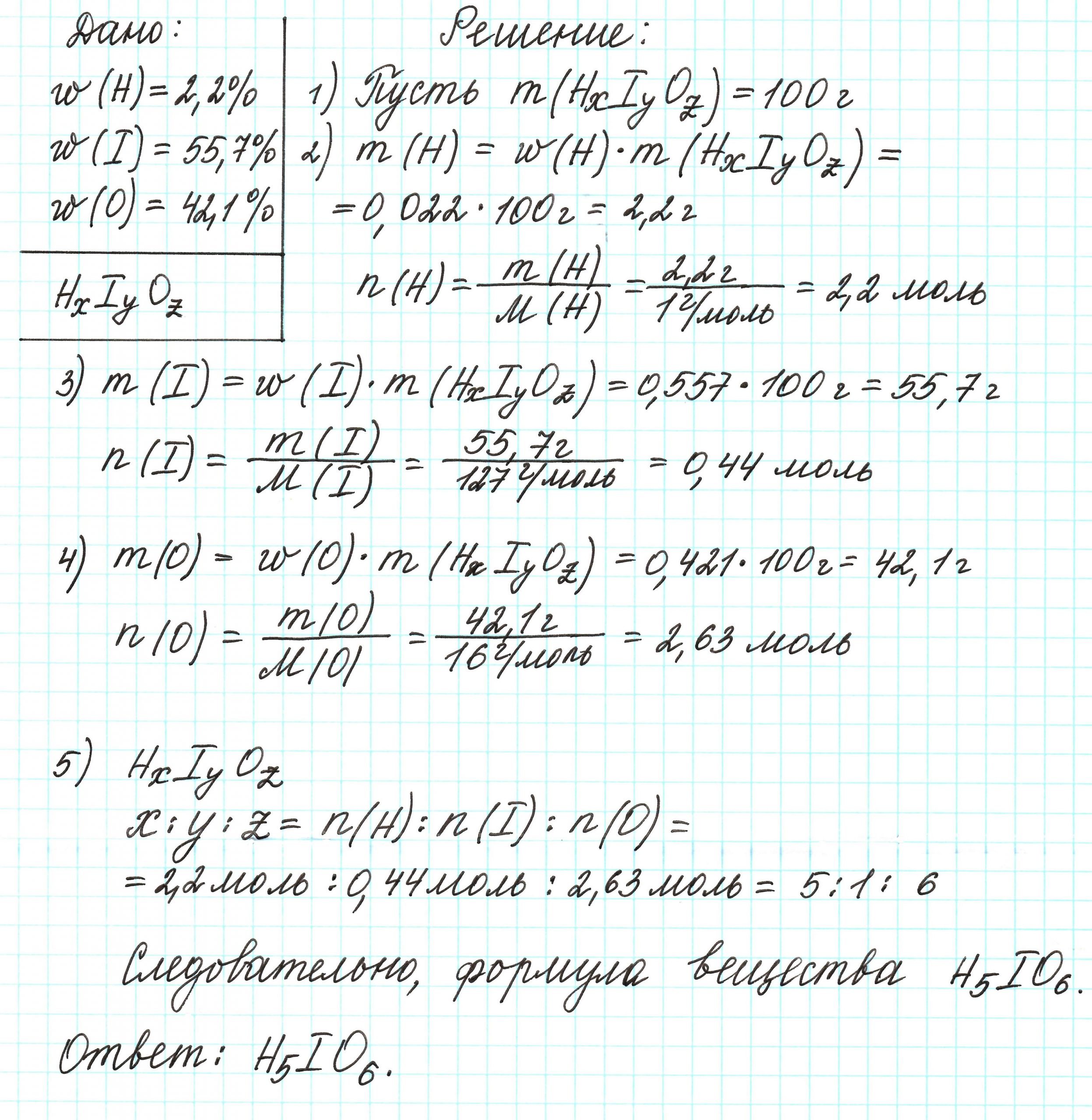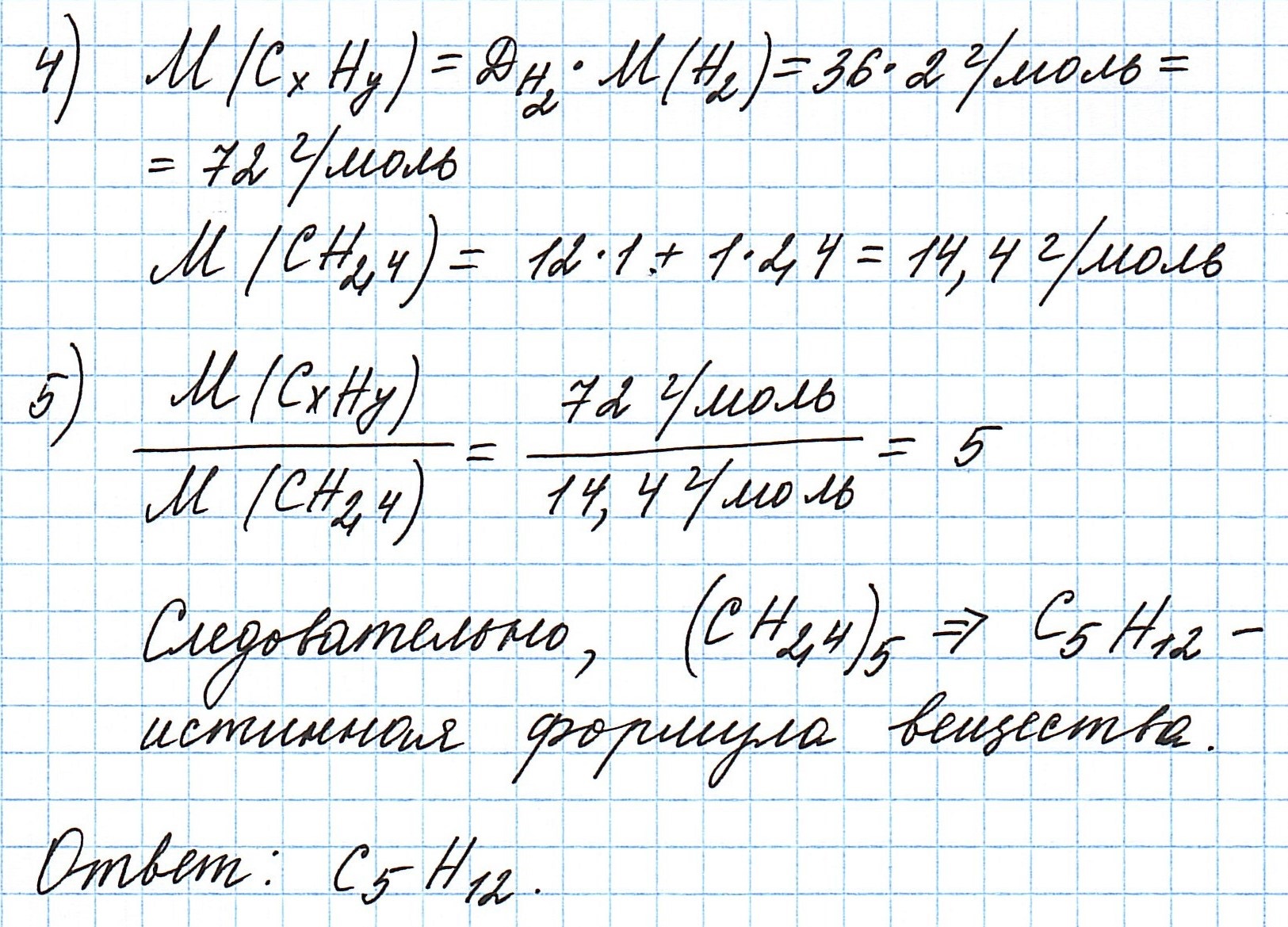Что означает данная формула
Урок 26 Бесплатно Формулы
Сегодня на уроке мы выясним, что называют формулой и где её применяют.
Разберем правила решения и оформления задач, решаемых с помощью формул.
Рассмотрим примеры таких задач и научимся работать с формулами: выражать неизвестные величины через известные.
Формулы
Математический язык- это формальный, искусственно созданный язык, который состоит из математических знаков, символов, терминов, выражений.
В отличие от естественных языков, этот язык более точный, логичный и краткий.
При переходе с разговорного языка на математический многие утверждения, правила, законы становятся яснее и прозрачнее.
Математика, физика, химия и многие другие науки используют язык математики, который в условной форме позволяет представить информацию наглядно и лаконично, не искажая ее при этом.
Естественными языками легче всего выражать качественные характеристики посредством красноречивых предложений.
Математический язык- это в большей степени количественный язык.
Одним из базовых элементов математического языка являются формулы.
У меня есть дополнительная информация к этой части урока!
Давайте разберёмся, что означает слово «Формула».
В толковом словаре русского языка Ожегова есть еще одно интересное толкование этого слова: формула- комбинация математических знаков, выражающая какое-нибудь утверждение
Обобщая все выше написанное, можно сказать, что формула- это правило (высказывание), записанное на математическом языке с помощью осмысленной комбинации знаков и символов.
Формулы представляют собой некоторые суждения, которые понятны любому человеку, любой национальности, и неважно каким разговорным языком человек владеет.
В формулу входят переменные. Она устанавливает взаимосвязь между величинами, входящими в нее.
Любые правила, записанные с помощью букв, будут являться примерами формул.
Вам уже известны некоторые математические формулы.
Приведем несколько примеров.
Правило нахождения периметра треугольника: РАВС = a + b + c— формула.
Правило нахождения периметра прямоугольника: Р = 2(a + b)— формула.
Пройти тест и получить оценку можно после входа или регистрации
Решение задач с помощью формул
Нам часто приходится сталкиваться с решением различных задач.
Существуют различные способы и методы решения задач.
Рассмотрим один из них: решение задач с помощью формул.
Процесс решения задач данным способом можно разделить на несколько основных этапов.
Данная последовательность действий не даст ответа на конкретную задачу, но сделает решение ее более понятным и быстрым и позволит решить даже самые непростые задачи.
Рассмотрим общие правила решения задач с помощью формул.
1. Внимательно прочитать, осмыслить и изучить условие задачи.
Следует установить то, что необходимо найти и что известно.
В задачах в основном содержится только существенная информация, т.е. те данные, которые могут быть использованы при их решении.
2. Для лучшего понимания задачи можно ее условия изобразить графически при помощи рисунка, схемы, чертежа и т.д.
С помощью иллюстрации легче понимать и воспринимать информацию.
3. Определить характерные черты задачи.
Следует понять, какого рода задача, чтобы выбрать верный путь ее решения.
Необходимо определить, какими величинами можно описать происходящие процессы, явления, действия, а также важно выяснить, из какой темы будут взяты формулы (если задача сложная, то могут понадобиться несколько формул).
4. Составить план решения задачи.
5. Выразить неизвестную величину через известные величины, т.е. вывести расчетную формулу.
6. Подставить известные числовые значения и произвести вычисления.
7. Оценить размерность (соответствие единиц измерения) величины, полученной в ответе, проверить найденный ответ на наличие вычислительных ошибок.
Чтобы верно и быстро решить задачу, важно не только действовать четко по определенному алгоритму, но и грамотно записывать и оформлять решение этой задачи.
Задачи, решаемые с помощью формул, удобно делить на два блока: «Дано» и «Решение».
В «Дано» обычно с помощью букв или символов записывают заданные величины и величины, которые требуется определить; т.е. кратко обозначают условие задачи.
Можно использовать любые буквы для обозначения заданных и искомых величин, но тогда необходимо делать краткое описание того, какую величину обозначает та или иная буква, выбранная вами.
Однако чаще всего буквенные обозначения величин, если они не указаны в условиях задачи, выбираются в соответствии с принятыми в науке символами.
Многие величины уже имеют специальные обозначения.
Каждая величина имеет единицу измерения.
Сразу в «Дано» переводят единицы измерения в единую систему, так как одна и та же величина должна быть выражена единой единицей измерения.
Иногда в задачах одноименные величины могут быть выражены разными числовыми мерами.
Например, расстояние может быть выражено в одной и той же задаче километрами, метрами и сантиметрами, или время может быть представлено в одном условии задачи в часах, в другом условии этой же задачи в минутах.
В таком случае необходимо выполнить перевод из разных единиц измерения в одну общую, которая будет фигурировать при числовых подсчетах.
У меня есть дополнительная информация к этой части урока!
Чаще всего выбор единиц измерения диктуется установленными международными нормами.
Наиболее широко используемой системой единиц в мире является единая интернациональная система. Называется она сокращенно «Система СИ».
Система СИ принята как основная система единиц в большинстве стран мира.
Страны, которые используют традиционные единицы, ввели коэффициенты и поправки, чтобы связать свои единицы измерения с системой СИ.
СИ создана на основе метрической системы, которая была создана французскими учеными. (с метрической системой мы немного познакомились, рассматривая тему «Отрезок. Длина отрезка.»).
Система СИ определяет семь основных единиц и производные единицы, а также набор приставок.
Системой СИ установлены стандартные сокращенные обозначения единиц.
Обзор формул
Если вы еще не Excel в Интернете, скоро вы увидите, что это не просто сетка для ввода чисел в столбцах или строках. Да, с помощью Excel в Интернете можно найти итоги для столбца или строки чисел, но вы также можете вычислять платежи по ипотеке, решать математические или инженерные задачи или находить лучшие сценарии в зависимости от переменных чисел, которые вы подключали.
Excel в Интернете делает это с помощью формул в ячейках. Формула выполняет вычисления или другие действия с данными на листе. Формула всегда начинается со знака равенства (=), за которым могут следовать числа, математические операторы (например, знак «плюс» или «минус») и функции, которые значительно расширяют возможности формулы.
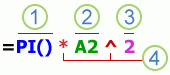
Ниже приведен пример формулы, умножающей 2 на 3 и прибавляющей к результату 5, чтобы получить 11.
Следующая формула использует функцию ПЛТ для вычисления платежа по ипотеке (1 073,64 долларов США) с 5% ставкой (5% разделить на 12 месяцев равняется ежемесячному проценту) на период в 30 лет (360 месяцев) с займом на сумму 200 000 долларов:
Ниже приведены примеры формул, которые можно использовать на листах.
=A1+A2+A3 Вычисляет сумму значений в ячейках A1, A2 и A3.
=КОРЕНЬ(A1) Использует функцию КОРЕНЬ для возврата значения квадратного корня числа в ячейке A1.
=СЕГОДНЯ() Возвращает текущую дату.
=ПРОПИСН(«привет») Преобразует текст «привет» в «ПРИВЕТ» с помощью функции ПРОПИСН.
=ЕСЛИ(A1>0) Анализирует ячейку A1 и проверяет, превышает ли значение в ней нуль.
Элементы формулы
Формула также может содержать один или несколько из таких элементов: функции, ссылки, операторы и константы.
1. Функции. Функция ПИ() возвращает значение числа Пи: 3,142.
2. Ссылки. A2 возвращает значение ячейки A2.
3. Константы. Числа или текстовые значения, введенные непосредственно в формулу, например 2.
4. Операторы. Оператор ^ («крышка») применяется для возведения числа в степень, а оператор * («звездочка») — для умножения.
Использование констант в формулах
Константа представляет собой готовое (не вычисляемое) значение, которое всегда остается неизменным. Например, дата 09.10.2008, число 210 и текст «Прибыль за квартал» являются константами. выражение или его значение константами не являются. Если формула в ячейке содержит константы, но не ссылки на другие ячейки (например, имеет вид =30+70+110), значение в такой ячейке изменяется только после изменения формулы.
Использование операторов в формулах
Операторы определяют операции, которые необходимо выполнить над элементами формулы. Вычисления выполняются в стандартном порядке (соответствующем основным правилам арифметики), однако его можно изменить с помощью скобок.
Типы операторов
Приложение Microsoft Excel поддерживает четыре типа операторов: арифметические, текстовые, операторы сравнения и операторы ссылок.
Арифметические операторы
Арифметические операторы служат для выполнения базовых арифметических операций, таких как сложение, вычитание, умножение, деление или объединение чисел. Результатом операций являются числа. Арифметические операторы приведены ниже.
Возведение в степень
Операторы сравнения
Операторы сравнения используются для сравнения двух значений. Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.
= (знак «больше или равно»)
Текстовый оператор конкатенации
Амперсанд ( &) используется для объединения (соединения) одной или нескольких текстовых строк в одну.
Соединение или объединение последовательностей знаков в одну последовательность
Выражение «Северный»&«ветер» дает результат «Северный ветер».
Операторы ссылок
Для определения ссылок на диапазоны ячеек можно использовать операторы, указанные ниже.
Оператор диапазона, который образует одну ссылку на все ячейки, находящиеся между первой и последней ячейками диапазона, включая эти ячейки.
Оператор объединения. Объединяет несколько ссылок в одну ссылку.
Оператор пересечения множеств, используется для ссылки на общие ячейки двух диапазонов.
Порядок выполнения Excel в Интернете формулах
В некоторых случаях порядок вычисления может повлиять на возвращаемое формулой значение, поэтому для получения нужных результатов важно понимать стандартный порядок вычислений и знать, как можно его изменить.
Порядок вычислений
Формулы вычисляют значения в определенном порядке. Формула всегда начинается со знака равно (=).Excel в Интернете интерпретирует знаки после знака равно как формулу. После знака равно вычисляются элементы (операнды), такие как константы или ссылки на ячейки. Они разделены операторами вычислений. Excel в Интернете вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.
Приоритет операторов
Если в одной формуле несколько операторов, Excel в Интернете выполняет операции в том порядке, который показан в таблице ниже. Если формула содержит операторы с одинаковым приоритетом, например операторы деления и умножения, Excel в Интернете эти операторы оцениваются слева направо.
Возведение в степень
Умножение и деление
Сложение и вычитание
Объединение двух текстовых строк в одну
Использование круглых скобок
Чтобы изменить порядок вычисления формулы, заключите ее часть, которая должна быть выполнена первой, в скобки. Например, следующая формула дает результат 11, так как Excel в Интернете умножение выполняется перед с добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.
Если же изменить синтаксис с помощью скобок, Excel в Интернете сбавляет 5 и 2, а затем умножает результат на 3, чтобы получить 21.
В следующем примере скобки, в которые заключена первая часть формулы, принудительно Excel в Интернете сначала вычислить ячейки B4+25, а затем разделить результат на сумму значений в ячейках D5, E5 и F5.
Использование функций и вложенных функций в формулах
Функции — это заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. Эти функции позволяют выполнять как простые, так и сложные вычисления.
Синтаксис функций
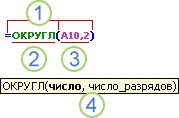
Приведенный ниже пример функции ОКРУГЛ, округляющей число в ячейке A10, демонстрирует синтаксис функции.
1. Структура. Структура функции начинается со знака равно (=), за которым следуют имя функции, открывая скобка, аргументы функции, разделенные запятой, и закрывая скобка.
2. Имя функции. Чтобы отобразить список доступных функций, щелкните любую ячейку и нажмите клавиши SHIFT+F3.
3. Аргументы. Существуют различные типы аргументов: числа, текст, логические значения (ИСТИНА и ЛОЖЬ), массивы, значения ошибок (например #Н/Д) или ссылки на ячейки. Используемый аргумент должен возвращать значение, допустимое для данного аргумента. В качестве аргументов также используются константы, формулы и другие функции.
4. Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Ввод функций
Диалоговое окно Вставить функцию упрощает ввод функций при создании формул, в которых они содержатся. При вводе функции в формулу в диалоговом окне Вставить функцию отображаются имя функции, все ее аргументы, описание функции и каждого из аргументов, текущий результат функции и всей формулы.
Чтобы упростить создание и редактирование формул и свести к минимуму количество опечаток и синтаксических ошибок, пользуйтесь автозавершением формул. После того как вы введите знак «= » (знак равно) и начинательные буквы или триггер отображения Excel в Интернете под ячейкой будет отображаться динамический список действительных функций, аргументов и имен, которые соответствуют этим буквам или триггеру. После этого элемент из раскрывающегося списка можно вставить в формулу.
Вложенные функции
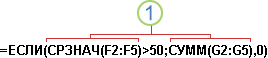
В некоторых случаях может потребоваться использовать функцию в качестве одного из аргументов другой функции. Например, в приведенной ниже формуле для сравнения результата со значением 50 используется вложенная функция СРЗНАЧ.
1. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.
Допустимые типы вычисляемых значений Вложенная функция, используемая в качестве аргумента, должна возвращать соответствующий ему тип данных. Например, если аргумент должен быть логическим, т. е. Если эта функция не работает, Excel в Интернете отобразит #VALUE! В противном случае TE102825393 выдаст ошибку «#ЗНАЧ!».
Использование ссылок в формулах
Ссылка указывает на ячейку или диапазон ячеек на сайте и сообщает Excel в Интернете, где искать значения или данные, которые вы хотите использовать в формуле. С помощью ссылок в одной формуле можно использовать данные, которые находятся в разных частях листа, а также значение одной ячейки в нескольких формулах. Вы также можете задавать ссылки на ячейки разных листов одной книги либо на ячейки из других книг. Ссылки на ячейки других книг называются связями или внешними ссылками.
Стиль ссылок A1
Стиль ссылок по умолчанию По умолчанию в Excel в Интернете используется стиль ссылок A1, который ссылается на столбцы буквами (от A до XFD, всего 16 384 столбца) и ссылается на строки с числами (от 1 до 1 048 576). Эти буквы и номера называются заголовками строк и столбцов. Для ссылки на ячейку введите букву столбца, и затем — номер строки. Например, ссылка B2 указывает на ячейку, расположенную на пересечении столбца B и строки 2.
Ячейка или диапазон
Ячейка на пересечении столбца A и строки 10
Диапазон ячеек: столбец А, строки 10-20.
Диапазон ячеек: строка 15, столбцы B-E
Все ячейки в строке 5
Все ячейки в строках с 5 по 10
Все ячейки в столбце H
Все ячейки в столбцах с H по J
Диапазон ячеек: столбцы А-E, строки 10-20
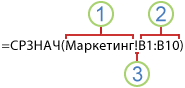
1. Ссылка на лист «Маркетинг».
2. Ссылка на диапазон ячеек с B1 по B10 включительно.
3. Ссылка на лист, отделенная от ссылки на диапазон значений.
Различия между абсолютными, относительными и смешанными ссылками
Стиль трехмерных ссылок
Удобный способ для ссылки на несколько листов Трехмерные ссылки используются для анализа данных из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка содержит ссылку на ячейку или диапазон, перед которой указываются имена листов. Excel в Интернете использует все таблицы, которые хранятся между начальным и конечним именами ссылки. Например, формула =СУММ(Лист2:Лист13!B5) суммирует все значения, содержащиеся в ячейке B5 на всех листах в диапазоне от листа 2 до листа 13 включительно.
При помощи трехмерных ссылок можно создавать ссылки на ячейки на других листах, определять имена и создавать формулы с использованием следующих функций: СУММ, СРЗНАЧ, СРЗНАЧА, СЧЁТ, СЧЁТЗ, МАКС, МАКСА, МИН, МИНА, ПРОИЗВЕД, СТАНДОТКЛОН.Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.
Трехмерные ссылки нельзя использовать в формулах массива.
Трехмерные ссылки нельзя использовать вместе с оператор пересечения (один пробел), а также в формулах с неявное пересечение.
Вставка или копирование Если вставить листы между листами 2 и 6, Excel в Интернете будет включать в расчет все значения из ячеек с A2 по A5 на добавленных листах.
Удалить Если удалить листы между листами 2 и 6, Excel в Интернете вы вычислите их значения.
Переместить Если переместить листы между листами 2 и 6 в место за пределами диапазона, на который имеется ссылка, Excel в Интернете удалит их значения из вычислений.
Перемещение конечного листа Если переместить лист 2 или 6 в другое место книги, Excel в Интернете скорректирует сумму с учетом изменения диапазона листов.
Удаление конечного листа Если удалить лист 2 или 6, Excel в Интернете скорректирует сумму с учетом изменения диапазона листов между ними.
Стиль ссылок R1C1
Можно использовать такой стиль ссылок, при котором нумеруются и строки, и столбцы. Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает на расположение ячейки с помощью R, за которым следует номер строки, и C, за которым следует номер столбца.
относительная ссылка на ячейку, расположенную на две строки выше в том же столбце
Относительная ссылка на ячейку, расположенную на две строки ниже и на два столбца правее
Абсолютная ссылка на ячейку, расположенную во второй строке второго столбца
Относительная ссылка на строку, расположенную выше текущей ячейки
Абсолютная ссылка на текущую строку
При записи макроса Excel в Интернете некоторые команды с помощью стиля ссылок R1C1. Например, если записать команду (например, нажать кнопку «Автоумма»), чтобы вставить формулу, в которую добавляется диапазон ячеек, Excel в Интернете записи формулы со ссылками с помощью стиля R1C1, а не A1.
Использование имен в формулах
Можно создавать определенные имена для представления ячеек, диапазонов ячеек, формул, констант и Excel в Интернете таблиц. Имя — это значимое краткое обозначение, поясняющее предназначение ссылки на ячейку, константы, формулы или таблицы, так как понять их суть с первого взгляда бывает непросто. Ниже приведены примеры имен и показано, как их использование упрощает понимание формул.
Пример использования диапазонов вместо имен
Как легко понять знаки Σ и П с помощью программирования
Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
КАК ВЫЧИСЛИТЬ ФОРМУЛУ ВЕЩЕСТВА
Способов, как определить формулу вещества, достаточно много. Все зависит от исходных данных. Наиболее разнообразны подобные вычисления в органической химии. И это не удивительно, так как органических соединений значительно больше, чем неорганических.
1.Понятие простейшей и истинной формулы вещества
В одних задачах на определение формулы вещества необходимо найти его простейшую формулу, а в других – истинную. В чем разница?
Так, например: СН2 – простейшая формула алкена – показывает, что на каждый 1 атом углерода приходится 2 водородных атома. То есть существует соотношение 1:2. Поэтому для нахождения простейшей (эмпирической) формулы вещества важно рассчитать количество вещества атомов, которые входят в его состав, то есть n(C) и n(H).
Например, для пропилена, относящегося к классу алкенов, истинная (молекулярная) формула будет C3H6. Она говорит о том, что молекула данного вещества включает 3 атома С и 6 атомов Н. Это вполне соответствует простейшей формуле, отвечающей соотношению атомов 1:2. Для нахождения истинной (молекулярной) формулы соединения требуется посчитать его относительную молекулярную (Mr) или молярную массу (M).
2.Массовая доля химического элемента: что означает и как высчитывается
Массовая доля – это отношение массы компонента системы к массе системы, выраженное в процентах или долях от единицы.
Молекула имеет массу. Все атомы в молекуле также имеют свои массы. Атомов одного химического элемента в молекуле может быть 1 или несколько. Важна масса всех атомов одного элемента. Если ее разделить на массу молекулы, то получится массовая доля этого элемента. Ее выражают либо в процентах, которые всегда меньше 100%, либо в долях от единицы, которые всегда меньше 1.
Пример 1. Каковы массовые доли элементов в оксиде железа (III) Fe2O3.
3.Как определить формулу вещества по массовым долям элементов
Нахождение формулы вещества по массовым долям элементов применимо как к органическим, так и к неорганическим соединениям.
Пример 2. Сероуглерод содержит 15,8% углерода по массе. Какова простейшая формула этого вещества?
Поскольку речь идет о массовых долях элементов, то необходимо знать массу вещества. В нашем случае – массу сероуглерода. В условии задачи о ней ничего не говорится. Поэтому допускаем, что масса вещества равна 100 г.
Почему 100 г? Это «круглое» число, и его использование облегчает все расчеты. Так как в итоге будем находить соотношения количеств веществ элементов, то какое-то особенное значение массы вещества не играет никакой роли.
Попробуйте ради эксперимента принять массу сероуглерода равной 23 г, 467 г и т.п. Результат будет один и тот же.
Допустим, что атомов углерода в молекуле х, а атомов серы – у. В таком случае формула вещества примет вид: СхSу.
Пример 3. Содержание углерода в углеводороде составляет 83,33%. Плотность паров соединения по водороду – 36. Какова молекулярная формула углеводорода?
Чтобы не загромождать записи, массовую долю элементов будем считать не в процентах, а в долях от единицы.
Пусть вас не удивляет получившаяся простейшая формула. Ведь, исходя из определения простейшей формулы, на каждый 1 атом углерода приходится 2,4 атома водорода. Это всего лишь соотношение. Соединения с формулой СН2,4 в принципе не существует. Не всегда простейшая и истинная формулы совпадают друг с другом.
А если полученная формула СН2,4 вас все же смущает, вы можете решать задачу и вторым способом. Но это несколько более сложный способ, когда требуется составить и решить уравнение с двумя неизвестными.
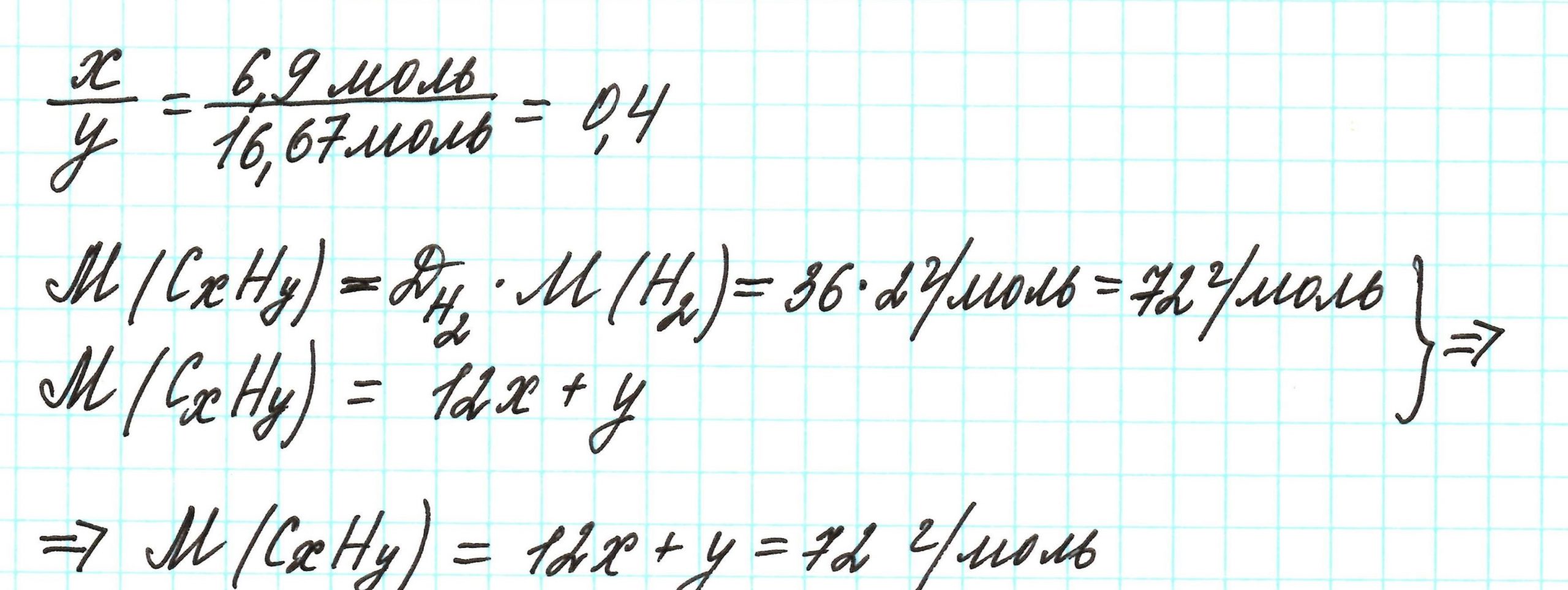
Не все химические вещества являются бинарными, то есть состоят из атомов двух химических элементов. Но в любом случае, алгоритм решения задачи тот же.
Пример 4. Некоторая кислота содержит водород (2,2%), иод (55,7%) и кислород (42,1%). Определите простейшую формулу этой кислоты.
4.Как определить формулу органического соединения
Определить формулу органического вещества можно не только зная массовые доли элементов в его составе.
4.1. Как определить формулу органического соединения
по общей молекулярной формуле вещества
Органические вещества сгруппированы по самостоятельным классам на основе общности строения и свойств. Каждый класс соединений характеризуется своей общей молекулярной формулой. Особенно это наглядно видно на примере углеводородов.
Если другие органические вещества рассматривать как их производные, в молекулы которых введена какая-либо функциональная группа, то и для них также можно составить общую молекулярную формулу.
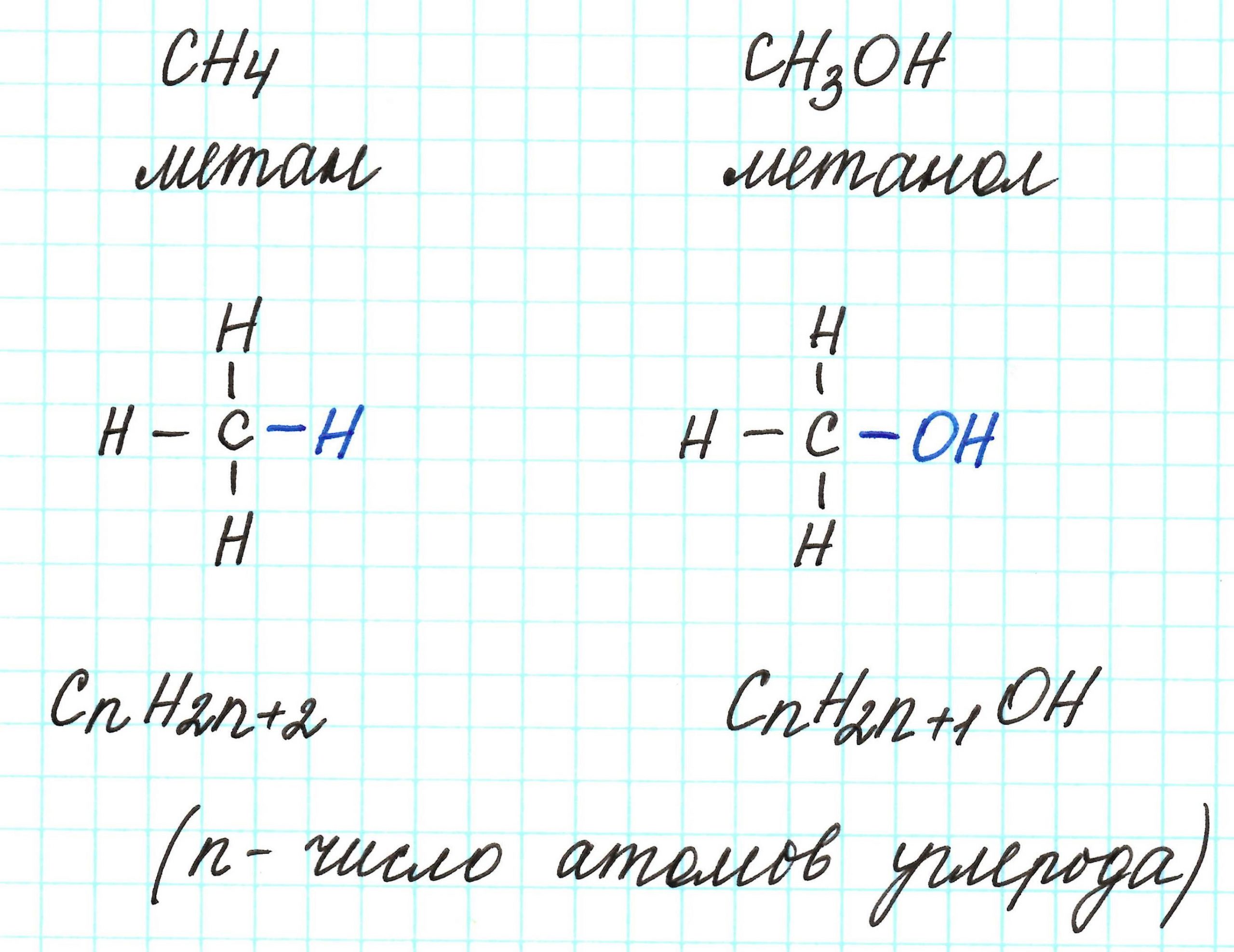
Предельные одноатомные спирты можно рассматривать как производные алканов, в молекулах которых 1 атом водорода замещен на гидроксильную группа –ОН. Таким образом, их общая молекулярная формула такая: СnH2n+1ОН.
Ниже в таблице приведены общие молекулярные формулы основных классов органических соединений.
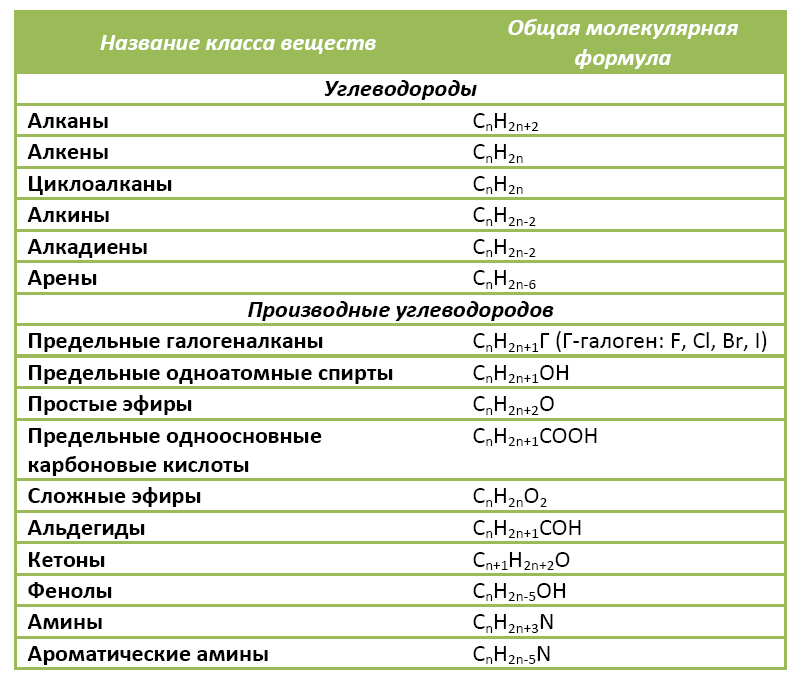
Пример 5. Плотность паров по воздуху некоторого алкана 4,414. Какова формула алкана?

4.2. Как определить формулу органического соединения
по продуктам его сгорания
Это еще один распространенный тип задач на определение формулы органического соединения.
Необходимо запомнить и понять основные моменты:
— так как все органические вещества содержат атомы С, Н, а также атомы О (кислородсодержащие соединения), то всегда при их сгорании выделяется углекислый газ СО2 и образуется вода Н2О;
— все углеродные атомы, входящие в состав органического соединения, окажутся в составе углекислого газа СО2; следовательно, n(С) как в соединении, так и в СО2 – это одна и та же величина;
— все атомы водорода Н, которые имеются в составе вещества, перейдут в состав воды Н2О; следовательно, n(Н) и в данном веществе, и в Н2О – это одна и та же величина;
— при сгорании веществ, включающих в себя азот (например, амины), кроме СО2 и Н2О, образуется еще и N2.
Разберем несколько примеров.
Пример 6. Сожгли 7,2 г углеводорода. Плотность его паров по водороду составляет 36. В результате реакции образовалось 22 г оксида углерода (IV) и 10,8 г воды. Какова молекулярная формула соединения?
Пример 7. В результате сгорания 4,8 г органического соединения выделилось 3,36 л (н.у.) оксида углерода (IV) и образовалось 5,4 г воды. Плотность паров искомого соединения по кислороду равна 1. Вычислите молекулярную формулу вещества.
Пример 8. Результатом сжигания 0,31 г газообразного органического соединения, имеющего плотность 1,384 г/л, стало выделение 0,224 л (с.у.) оксида углерода (IV), 0,112 л азота и образование 0,45 г воды. Вычислите молекулярную формулу этого вещества.

5. Как определить формулу вещества: комбинированные задачи
Наибольший интерес и некоторую трудность представляют комбинированные задачи, сочетающие в себе необходимость найти формулу соединения:
— используя приемы, применяемые в рассмотренных выше задачах;
— используя сведения не только о химических, но и физических свойствах вещества.
Вот несколько примеров.
Пример 9. Какова молекулярная формула предельного углеводорода, при полном сгорании 8,6 г которого выделилось 13, 44 л (н.у.) оксида углерода (IV).
1) известен класс вещества, поэтому возможно применить его общую молекулярную формулу;
2) речь идет о сгорании вещества, поэтому количество атомов в составе молекулы будем искать, используя данные о продукте сгорания – СО2.
Пример 10. Алкен нормального строения содержит двойную связь при первом углеродном атоме. Образец этого алкена массой 0,7 г присоединил бром массой 1,6 г. Вычислите формулу алкена и назовите его.
В предлагаемых условиях:
1) известен класс вещества, следовательно, применим его общую молекулярную формулу;
2) речь идет об одном из химических свойств: способности алкенов присоединять галогены по месту разрыва двойной связи.
Пример 11. После полного сжигания в кислороде арена, имевшего массу 0,92 г, выделился оксид углерода (IV). Пропуская газ через избыток раствора щелочи Ca(OH)2, получили 7 грамм осадка. Какова молекулярная формула арена?
В предлагаемой задаче:
1) известен класс вещества;
2) речь идет о сжигании соединения и образовании в качестве продукта горения углекислого газа, который при взаимодействии со щелочью Са(ОН)2 привел к выпадению осадка известной массы.
Следующий пример очень характерен для задач, встречающихся в заданиях второй части ЕГЭ по химии.
Пример 12. Некоторое соединение, образующее альдегид в реакции окисления, взаимодействует с избытком бромоводородной кислоты, образуя 9,84 г продукта (выход составляет 80% от теоретического), имеющего плотность паров по Н2 61,5. Определите строение этого соединения, а также его массу, вступившую в реакцию?
1) говорится о химических свойствах искомого соединения; анализируя их, приходим к выводу, что заданным веществом является предельный одноатомный спирт;
2) известна общая молекулярная формула предельных одноатомных спиртов;
3) более подробно говорится о взаимодействии заданного вещества с бромоводородной кислотой; спирт, реагируя с HBr, дает галогеналкан, для которого известны его масса, практический выход и относительная плотность по Н2; именно от этих данных и нужно отталкиваться при решении данной задачи.
Итак, способов, как определить формулу вещества, действительно, множество. Мы рассмотрели лишь основные из них. Важно правильно уяснить понятия «простейшая формула вещества» и «истинная формула вещества», чтобы не путать их.
Чтобы самыми первыми узнавать о новых публикациях на сайте, присоединяйтесь в нашу группу ВКонтакте.
Пожалуйста, оцените публикацию