Что означает и как определяется период полупревращения в реакциях первого порядка
Период полупревращения
Мы уже сталкивались с подобным понятием в гл. 1 при обсуждении явления радиоактивности (разд. 1.3), хотя в том случае вместо понятия период полупревращения используется родственный термин-«период полураспада». Период полупревращения-это время, необходимое для того, чтобы исходная концентрация реагента уменьшилась вдвое. Измерение периода полупревращения приносит большую пользу при исследованиях порядка реакции. Например, в реакциях первого порядка период полупревращения г1/2 связан с константой скорости к простым соотношением
Скорость радиоактивного распада не зависит от температуры. Тем не менее, радиоактивный распад тоже протекает по кинетическому уравнению первого порядка. Период полураспада радиоактивного процесса можно определить, измеряя уровень радиоактивности через равные промежутки времени и строя кривую распада. На таком подходе основан, например, метод датировки событий с помощью радиоактивного углерода, описанный в разд. 1.3.
ЗАВИСИМОСТЬ КОНСТAHТЫ СКОРОСТИ ОТ ТЕМПЕРАТУРЫ УРАВНЕНИЕ АРРЕНИУСА
В качестве приближенного правила можно запомнить, что скорость любой химической реакции становится вдвое больше при повышении температуры на каждые 10 К. Это правило позволяет предположить, что между скоростью реакций и температурой есть зависимость
Шведский физикохимик Сванте Аррениус получил Нобелевскую премию по химии в 1903 г. за созданную теорию электролитической диссоциации. В своей докторской диссертации (Уппсальский университет) Аррениус высказал предположение, что такие «молекулы» как хлорид натрия, самопроизвольно распадаются i растворе, образуя ионы, которые выполняют роль реагентов при электролизе. Однако более всего Аррениус известен своим уравнением, определяющим температурную зависимость константы скорости реакции должна существовать экспоненциальная зависимость.
Точное соотношение межд скоростью реакций и температурой впервые установил шведский химик Аррениус 1889 г. Это соотношение, получившее название уравнения Аррениуса, имеет вид
В логарифмической форме уравнение Аррениуса приобретает вид
Если перейти от натуральных логарифмов к десятичным, последнее соотношенв сводится к виду
Именно эта форма уравнения Аррениуса наиболее употребительна.
Для определения констант А и Еа, характеризующих конкретную реакцию, строя график зависимости Ig к от величины 1/Т. (Напомним, что температура должна быт выражена в абсолютной шкале.) Тангенс угла наклона графика к оси абсцисс дае величину Ea/2,303RT. Для определения константы Аррениуса А следует подставить уравнение Аррениуса все остальные известные значения.
Кинетические уравнения. Тема: Порядок реакции. Период полупревращения
Тема. Порядок реакции. Период полупревращения.
Мотивация изучения темы. Химическая кинетика является разделом физической химии, занимающимся изучением скорости и механизмом протекания реакций. На основе исследований строят гипотетическую схему, позволяющую объяснить всю совокупность известных экспериментальных фактов и позволяющую целенаправленно влиять на ту или иную химическую реакцию, осуществлять производственный синтез химических веществ.
Большое значение имеет кинетика и для фармации. Действие различных лекарственных веществ обуславливается в значительной степени скоростью реакций, происходящих в организме. При хранении лекарственных форм могут протекать различные реакции, скорость которых определяет срок годности лекарств.
В фармации используются фармакокинетика и фармакодинамика.
Фармакокинетика изучает распределение во времени фармакологически активных веществ и их метаболитов (продуктов их превращений) в различных частях живого организма (например, в волосах, слюне, в крови, в печени и в других внутренних органах). В отличии от биохимии фармакокинетика не занимается механизмами превращения инородных веществ (в частности лекарственных препаратов).
Фармакодинамика изучает действие во времени на живой организм различных фармакологически активных веществ.
Цель. Приобрести навыки определения кинетических характеристик реакций.
Задания для самостоятельной работы студента во внеучебное время (самоподготовка).
А. Контрольные вопросы.
Б. Список рекомендуемой литературы.
В. Обучающий материал.
Химическая кинетика изучает скорости химических реакций, их зависимость от различных факторов и механизмы реакций. Последовательность и характер стадий химических реакций называют механизмом реакции.
По механизму различают простые и сложные реакции. Простые реакции осуществляются посредством однотипных элементарных актов. Под элементарным актом понимают единичный акт взаимодействия или превращения частиц, в результате которого образуются новые частицы продуктов реакции или промежуточных соединений; В элементарном акте принимает участие одна или две частицы (реже три).
Для осуществления сложных реакций необходимы разнотипные (не менее двух) элементарные акты. Различают следующие типы сложных реакций: параллельные, последовательные, сопряженные, цепные.
пользуются понятием средней скорости в данном интервале времени Дt:
Истинная скорость (в любой момент времени) определяется первой производной концентрации во времени 
Константа скорости зависит от тех лее факторов, что и скорость химической реакции, но не зависит от концентрации реагирующих веществ.
Величина p+q определяет порядок кинетического уравнения реакции, который показывает, каким образом скорость реакции зависит от концентрации реагентов. Порядок кинетического уравнения может принимать значения 0, 1, 2 и более, он может быть также дробным.
Кинетические расчеты позволяют ответить на следующие вопросы:
1) сколько времени требуется для уменьшения концентрации исходного вещества до заданного уровня? (так, например, можно определить оптимальные промежутки времени между приемами лекарственного средства);
2) какой будет концентрация исходного вещества по истечении заданного промежутка времени? (так оценивается, например, остаточное количество токсиканта).

Примерами реакций нулевого порядка являются фотохимические, ферментативные и
когда реагирующее вещество взято в большом избытке или убыль его постоянно восполняется.
Для реакций первого порядка: V = кс;,
Отсюда 

Период полупревращения для реакции первого порядка (подставили в уравнение (1)
вместо С концентрацию со/2):
Период полупревращения для реакции первого порядка не зависит от концентрации исходного вещества. К реакциям первого порядка относят большинство реакций гидролиза органических соединений, процессы выведения лекарственного препарата из организма, разложение лекарственных препаратов при хранении, реакции радиоактивного распада.
Для реакции второго порядка: V = kc1c2. Если концентрации реагирующих веществ равны, то V=kc2. 


Если исходные концентрации реагирующих веществ, вступивших в реакцию, разные, то
Период полупревращения для реакции второго порядка обратно пропорционален начальной концентрации реагирующих веществ.
Кинетике второго порядка подчиняются такие простые бимолекулярные реакции, как, например, щелочной гидролиз сложного эфира.
Из приведенных уравнений можно сделать следующие выводы:
величина константы скорости уравнения первого порядка не зависит от способа выражения концентрации, а констант нулевого и второго порядков зависит. Например, если концентрацию выразить не в моль на л, а в миллимоль на литр, то величина константы скорости кинетических уравнений реакции нулевого порядка увеличится в 1000 раз, а величина константы скорости кинетических уравнений реакций второго порядка в 1000 раз уменьшится; величины констант скорости кинетических уравнений реакций всех порядков зависят от выбранной единицы времени. Например, если время выразить не в секундах, а в минутах, то величины констант возрастут в 60 раз; период полупревращения реакций первого порядка не зависит от начальной концентрации реагента, период полупревращения реакций нулевого порядка возрастает при увеличении с0, а реакций второго порядка уменьшается. Анализируя зависимость периода полупревращения реакции от начальной концентрации реагента, можно определить порядок реакции.
Определение порядка реакции по периоду полупревращения
В методе определения порядка реакции по периоду полупревращенияиспользуют различный характер зависимости t1/2 от начальной концентрации реагента. Для реакций нулевого порядка t1/2 прямо пропорционально начальной концентрации реагента (уравнение (260)), для реакций первого порядка не зависит от начальной концентрации реагирующего вещества (уравнение (265)), для реакций второго порядка – обратно пропорционально начальной концентрации (уравнение (269)).
| Реакция 0-го порядка | Реакция 1-го порядка | Реакция 2-го порядка | |||
 | 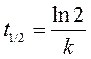 |  | |||
| с0, М | t1/2, с | с0, М | t1/2, с | с0, М | t1/2, с |
| 0,1 | 35,2 | 0,05 | 14,5 | 0,2 | |
| 0,2 | 70,0 | 0,15 | 14,6 | 0,4 | |
| 0,4 | 0,25 | 14,3 | 0,6 |
Для определения порядка изучаемой реакции необходимо экспериментально определить время полупревращения для нескольких начальных концентраций реагентов и установить, какая зависимость существует между ними. Для этого вначале анализируют экспериментальные данные в таблице, а затем, если зависимость между временем полупревращения и начальной концентрацией есть, строят в соответствующих координатах график, подтверждающий вид этой зависимости.
Значение константы скорости реакции находят по наклону прямой в соответствующих координатах используя или уравнение (260) (кинетика 0-го порядка), или (269) (кинетика 2-го порядка) или усреднением значений t1/2 и расчетом константы по уравнению (265), если исследуемая реакция подчиняется кинетике 1-го порядка.
Дифференциальные методы
Метод Вант-Гоффа
Дифференциальный метод, предложенный Вант-Гоффом, заключается в следующем. Пусть изучается кинетика химической реакции
Если начальная концентрация реагента В значительно больше начальной концентрации реагента А, то концентрация В в процессе протекания реакции изменяется незначительно и может быть принята постоянной (метод избытка реагента). Тогда кинетическое уравнение:
 | (271) |
 , , | (272) |
где 
Логарифмирование последнего уравнения приводит к линеаризованному уравнению:
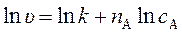 . . | (273) |
Определяя в опытах скорость реакции при различных начальных концентрациях реагирующих веществ и строя график зависимости логарифма скорости реакции от логарифма концентрации, определяют коэффициент наклона полученной прямой, который будет равен порядку реакции по веществу, концентрация которого изменялась. Значение lnu при ln cA = 0 равно lnk. Отсюда находят константу скорости химической реакции k в уравнении (272).
Этот метод можно применять в двух вариантах. В первом варианте определяют скорость реакции как производную dc/dt при разных начальных концентрациях. Проводят касательные к кривым в момент начала реакции.
Во втором варианте проводят только один опыт. Обработка кинетической кривой заключается в расчете наклонов касательных к кривой в различные моменты времени, соответствующие различным значениям концентраций реагентов.
Результаты, полученные в том и другом варианте, используются для построения зависимости логарифма скорости от концентрации реагента.
Примеры решения задач
1. Определить методом подстановки порядок и константу скорости реакции A ® … по зависимости концентрации реагента от времени, прошедшего с момента начала реакции. Температура 298 К.
| № | t, c | cA, М | № | t, c | cA, М |
| 0,180 | 0,0346 | ||||
| 0,128 | 0,0249 | ||||
| 0,0929 | 0,0177 | ||||
| 0,0681 | 0,0129 | ||||
| 0,0474 | 0,0092 |
| № | t, c | cA, М | Константа для реакции |
| 0 порядка | 1 порядка | 2 порядка | |
| 0,180 | – | – | – |
| 0,128 | 0,000520 | 0,00341 | 0,0226 |
| 0,0929 | 0,000436 | 0,00331 | 0,0260 |
| 0,0681 | 0,000373 | 0,00324 | 0,0304 |
| 0,0474 | 0,000332 | 0,00334 | 0,0389 |
| 0,0346 | 0,000291 | 0,00330 | 0,0467 |
| 0,0249 | 0,000259 | 0,00330 | 0,0577 |
| 0,0177 | 0,000232 | 0,00331 | 0,0728 |
| 0,0129 | 0,000209 | 0,00330 | 0,0900 |
| 0,0092 | 0,000190 | 0,00330 | 0,1146 |
| Среднее значение константы, с –1 | 0,00331 |
2. Определить графическим методом порядок и константу скорости реакции A ® … по зависимости концентрации реагента от времени, прошедшего с момента начала реакции. Температура 298 К.
| № | t, c | cA, М | № | t, c | cA, М |
| 0,180 | 0,0273 | ||||
| 0,0907 | 0,0241 | ||||
| 0,0590 | 0,0206 | ||||
| 0,0408 | 0,0193 | ||||
| 0,0328 | 0,0162 |
Для определения порядка реакции этим методом рассчитаем по экспериментальным данным значения ln с, 1/с и построим графики зависимостей «с – t«, «ln с – t«, «1/с – t«, в которых линеаризуются кинетические уравнения (258), (262) и (267) реакций 0-го, 1-го и 2-го порядков соответственно.
| № | t, c | cA, М | ln [с, М] | 1/с, М –1 |
| 0,180 | –1,715 | 5,56 | ||
| 0,0907 | –2,400 | 11,0 | ||
| 0,0590 | –2,830 | 16,9 | ||
| 0,0408 | –3,199 | 24,5 | ||
| 0,0328 | –3,417 | 30,5 | ||
| 0,0273 | –3,601 | 36,6 | ||
| 0,0241 | –3,726 | 41,5 | ||
| 0,0206 | –3,882 | 48,5 | ||
| 0,0193 | –3,948 | 51,8 | ||
| 0,0162 | –4,123 | 61,7 |
| Зависимость для изучаемой реакции является прямолинейной, если использовать уравнение (267), выведенное для кинетики 2-го порядка. Следовательно, изучаемая реакция является реакцией второго порядка по реагенту А. |  |
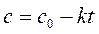 | |
 |  |
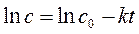 | 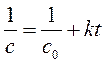 |
Константа скорости реакции в соответствии с уравнением (267) равна коэффициенту наклона 6,10×10 –2 л/(моль×с) в уравнении прямой, которое найдено методом наименьших квадратов.
3. Определить порядок и константу скорости реакции A ® … по времени полупревращения, используя экспериментальные данные, полученные при 298 К
| с0А, М | t1/2, с |
| 0,0317 | 26,9 |
| 0,0528 | 44,8 |
| 0,0916 | 81,5 |
| 0,134 | |
| 0,294 | |
| 0,403 |
Анализ экспериментальной зависимости времени полупревращения от начальной концентрации реагента А (таблица) позволяет из уравнений (260), (265) и (269)

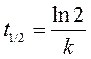

сразу отбросить второе (так как в соответствии с этим уравнением время полупревращения должно быть постоянным, а, судя по таблице, оно не постоянно) и третье уравнение (так как в соответствии с этим уравнением время полупревращения должно уменьшаться с увеличением начальной концентрации реагента, а оно увеличивается).
Остается первое уравнение, выведенное для кинетики 0-го порядка, однако необходимо проверить, действительно ли время полупревращения реагента А, найденное в эксперименте, прямо пропорционально начальной концентрации реагента. Для этого построим график зависимости в координатах «t1/2 – c0«. Если в этих координатах зависимость будет иметь вид прямой, проходящей через начало координат, как и график уравнения (260), то это будет являться подтверждением того, что исследуемая реакция является реакцией 0-го порядка.
Прямолинейность графика и малая величина отрезка, отсекаемого на оси ординат при t1/2 = 0 (2,3), подтверждают вывод о том, что исследуемая реакция имеет 0-ой порядок по реагенту А.
Константу скорости реакции находят из уравнения (260), которое, если выделить коэффициент перед начальной концентрацией, примет вид:

Расчет коэффициентов прямой (t1/2 = 848,1с0 + 2,3), выполненный по методу наименьших квадратов, приводит к ненулевому значению ординаты при с0 = 0 (t1/2 = 2,3). Этим отличием от нуля, которое возникает из-за ошибок, допущенных в эксперименте в определении времени и концентраций, в нашем случае можно пренебречь, так как ошибка в определении этого коэффициента прямой больше самого значения коэффициента (подробности расчета здесь не приводим).
и значение константы скорости равно

4. Монохлоруксусная кислота при температуре 298 К гидролизуется (вода в большом избытке)
Были проведены четыре эксперимента, в которых измерялась концентрация монохлоруксусной кислоты от времени (начальная концентрация кислоты была различна)
| t, мин | ||||
| c1, М | 0,129 | 0,119 | 0,101 | 0,0925 |
| c2, М | 0,0867 | 0,0787 | 0,0669 | 0,0616 |
| c3, М | 0,0508 | 0,0466 | 0,0396 | 0,0363 |
| c4, М | 0,0259 | 0,0237 | 0,0200 | 0,0186 |
Методом Вант-Гоффа определить порядок реакции и рассчитать кажущуюся константу скорости реакции.
Так как вода взята в большом избытке, то можно применить метод Вант-Гоффа. Скорость реакцииравна (А – монохлоруксусная кислота)
По первым двум колонкам таблицы рассчитаем значения средних скоростей реакции (уравнение (252)) и соответствующие им средние значения концентраций (уравнение (253)), а также их натуральные логарифмы (в точных расчетах используют средние значения концентраций по времени; в ориентировочных эту величину можно заменить средней по концентрации).
| cсред | uсред | ln cсред | ln uсред |
| 0,124 | 0,0000500 | –2,087 | –9,903 |
| 0,0827 | 0,0000400 | –2,493 | –10,127 |
| 0,0487 | 0,0000210 | –3,022 | –10,771 |
| 0,0248 | 0,0000110 | –3,697 | –11,418 |
Для нахождения порядка и константы скорости реакции по коэффициентам уравнения (273) строим график в координатах «lnu – ln cA«.
Угловой коэффициент уравнения рассчитанный по графику (рисунок) близок к 1; из этого следует, что порядок реакции по монохлоруксусной кислоте близок к 1, а кажущаяся константа скорости в уравнении (272) равна
Порядок реакции. Уравнение кинетики 1-го и 2-го порядка. Период полупревращения.
22. Зависимость скорости реакции от температуры. Температурный коэффициент скорости реакции.
При повышении температуры в значительной степени увеличивания скорость химических реакций. Это увеличение можно характеризовать при помощи температурного коэффициента скорости реакции, который представляет собой отношение констант скоростей при изменении температуры на 10°. По приближенному правилу (эмпирическое правило Вант Гоффа) повышение температуры на 10° вызывает увеличение скорости реакции примерно в 2 — 4 раза. Более точно зависимость скорости реакции от температуры выражается уравнением Аррениуса. Уравнение показывает, что логарифм отношения констант находится в линейной зависимости от величины, обратной температуре (1/Т). Экспериментальные исследования показывают, что, пользуясь уравнением Аррениуса, можно достаточно точно определить действительные изменения скорости реакций с изменением температуры. Таким образом, для химических процессов, протекающих в организме, выявляется так называемый «температурный оптимум», который для теплокровных животных лежит в интервале примерно 36—42° С.
Возрастание скорости реакции с ростом температуры принято характеризовать температурным коэффициентом скорости реакции — числом, показывающим, во сколько раз возрастает скорость данной реакции при повышении температуры системы на 10 градусов. Температурный коэффициент различных реакций различен. При обычных температурах его значение для большинства реакций лежит в пределах от 2 до 4. Это на первый взгляд небольшое значение температурного коэффициента обусловливает, однако, большое возрастание скорости реакции при значительном повышении температуры. Например, если температурный коэффициент равен 2,9, то при возрастании температуры на 100 градусов скорость реакции увеличивается на 2,9’°, т. е, приблизительно в 50000 раз.
Дата добавления: 2015-02-10 ; просмотров: 1338 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ








