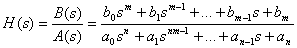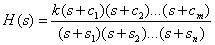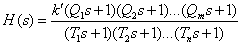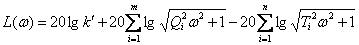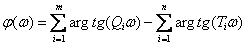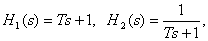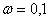Что означает идентификация математической модели
Идентификация модели
Идентификация модели (model identification). Под идентификацией модели принято понимать выбор переменных модели, а также параметров ее уравнений с последующей их оценкой на основе статистических данных, полученных в результате наблюдения или эксперимента (см. Оценка параметров модели).
Эконометрическая модель строится в форме системы одновременных уравнений, число которых должно быть равно числу неизвестных, под ними в эконометрическом уравнении понимаются текущие эндогенные переменные.
Уравнение называется точно идентифицированным, если число входящих в него текущих эндогенных переменных n на единицу больше количества предопределенных переменных, т.е. взятых вместе экзогенных и лаговых эндогенных переменных, содержащихся во всех уравнениях системы, кроме данного. Если первых меньше названного числа, то уравнение называется недоидентифицированным, если больше — сверхидентифицированным. В первом случае система уравнений (т.е. система, содержащая хотя бы одно недоидентифицированное уравнение) — неразрешима; во втором случае для ее решения требуются специальные приемы.
Смотреть что такое «Идентификация модели» в других словарях:
идентификация модели — Под идентификацией модели принято понимать выбор переменных модели, а также параметров ее уравнений с последующей их оценкой на основе статистических данных, полученных в результате наблюдения или эксперимента (см. Оценка параметров модели).… … Справочник технического переводчика
Идентификация объекта — [object identification] 1. Определение характеристик объекта и выявление приложенных к нему воздействий с помощью наблюдения за его входами и выходами и статистической обработки полученных данных. Иными словами, И.о. означает отождествление ему… … Экономико-математический словарь
идентификация объекта — 1. Определение характеристик объекта и выявление приложенных к нему воздействий с помощью наблюдения за его входами и выходами и статистической обработки полученных данных. Иными словами, И.о. означает отождествление ему как оригиналу некоторой… … Справочник технического переводчика
Идентификация портфельных рисков — Идентификация портфельных рисков процесс, который включает выявление рисков, которые могут повлиять на данный портфель и документирование их параметров и характеристик. Содержание 1 Место в системе управления портфелем проектов … Википедия
Идентификация систем — Идентификация систем математический аппарат для построения математических моделей динамической системы по измеренным данным. Математическая модель в данном контексте означает математическое описание динамики поведения какой либо системы или … Википедия
идентификация (в теории управления) — идентификация Процесс определения значений параметров математической модели процессов в объекте (в заданном классе моделей) по значениям координат объекта, измеряемым в процессе функционирования. [Сборник рекомендуемых терминов. Выпуск 107.… … Справочник технического переводчика
идентификация — 4.15 идентификация (identification): Процесс последовательного сопоставления полученного изображения лица со множеством изображений лиц для обнаружения похожего изображения; сопоставление 1:N («один ко многим»). Источник … Словарь-справочник терминов нормативно-технической документации
ИДЕНТИФИКАЦИЯ — процесс неосознаваемого отождествления себя с субъектом общения, деятельности (личностью, социальной общностью, нацией и т. п.), с объектом идентификации (с другим человеком, с определенной группой, общностью людей, другой нацией, народностью), в … Энциклопедический словарь по психологии и педагогике
идентификация домена — 3.15 идентификация домена (domain identification): Фаза модели предприятия, которая идентифицирует домен предприятия, моделируемый в отношении его бизнес задач, входов и выходов домена предприятия и их соответствующих происхождений и назначений.… … Словарь-справочник терминов нормативно-технической документации
Динамическая идентификация объектов управления
Введение
Идентификация объектов управления — совокупность методов для построения математических моделей объекта по данным наблюдений.
Математическая модель в данном контексте означает математическое описание поведения какого-либо объекта или процесса в частотной или временной области, к примеру, физических процессов (движение механической системы под действием внешней силы [1]), экономического процесса (влияние смены курса валют на потребительские цены на товары [2]).
В настоящее время эта область теории управления находит широкое применение на практике и поэтому интересна для рассмотрения.
Область динамической идентификации объектов управления в связи с различной природой самих объектов достаточно обширна, поэтому для начала ограничимся рассмотрением методов обработки так называемой кривой разгона.
Кривой разгона называют процесс изменения во времени выходной переменной, вызванный ступенчатым входным воздействием. Кривая разгона служит для определения динамических свойств объекта.
Постановка задачи
1. Построить математические модели динамической идентификации объекта управления по нормированной переходной характеристике (кривой разгона):
• Методом наименьших квадратов с использованием производных;
• Модифицированным методом площадей.
2. Определить и сравнить адекватность полученных математических моделей объекту управления.
Идентификация состоит в отыскании для объекта адекватной ему модели. Различают структурную и параметрическую идентификацию. При структурной идентификации определяется форма модели из некоторого заданного класса функций, при параметрической идентификации определяются параметры модели.
Если выходные сигналы объекта Y(t) полностью определяются наблюдаемыми входными воздействиями X(t), то для его идентификации достаточно использовать методы активного эксперимента.
Исходной информацией является экспериментально снятая кривая разгона – реакция объекта Y(t) на поданное входное воздействие X(t) в интервале времени 0≤t≤T.
Это структурная схема модели объекта с операторной передаточной функцией W(p). Уравнение динамической характеристики объекта можно условно представить в следующем виде:
(1)
где 
Схема для определения времени запаздывания и коэффициента усиления объекта:
Входные и выходные величины, как правило, масштабируются в стандартном диапазоне от 0 до 1 (нормируются):
После определения k и 

Структурная идентификация объекта
При структурной идентификации априорная информация об объекте используется для определения структуры модели.
Уравнение динамики, как правило, выбирается из класса линейных или линеаризованных характеристик. В нормированных координатах модель объекта с сосредоточенными параметрами, одним входным и одним выходным сигналом является обыкновенным дифференциальным уравнением с постоянными коэффициентами:

где коэффициенты 

По виду кривой разгона можно приближённо определить порядок будущей модели, например, для объекта первого порядка:
Для объектов более высоких порядков:
Обычно X(t) – ступенчатая функция, поэтому порядок уравнения (1) может быть приближенно определен по форме кривой разгона объекта. Если эта характеристика не имеет точек перегиба, то n = 1. Если есть перегиб при t = tп, и tп / T 2. Однако можно снизить порядок модели, вводя фиктивное запаздывание.
Влияние погрешности измерения X(t) и Y(t) и погрешности численных методов обработки информации обычно делает нецелесообразным использование моделей выше третьего-четвертого порядка.
Параметрическая идентификация объекта
При параметрической идентификации данные об объекте обрабатываются для получения о нем апостериорной информации. При этом оцениваются параметры выбранной модели. В простейших случаях такая оценка может выполняться по графику переходной характеристики.
Параметрическая идентификация методом наименьших квадратов с использованием производных
Для идентификации объекта произвольного порядка используется метод наименьших квадратов, требующий минимизации среднего квадрата невязки правой и левой частей уравнения (2):

где: 

Решение задачи (3) сводится к решению системы:

Преобразуя (4) в соответствии с уравнением (3), можно получить систему линейных алгебраических уравнений:

Для решения системы (5) относительно неизвестных параметров 


Погрешность численного дифференцирования, как правило, достаточно высока, поэтому схему определения коэффициентов, 
Параметрическая идентификация модифицированным методом площадей
Для создания модели средствами Python, модификация метода площадей состоит в неизменном масштабе времени. В классическом варианте вводят новый масштаб времени, что при численном решении приводит к дополнительной погрешности.
Обычно, выражение для передаточной функции ищут в виде одной из трех математических моделей:
Выражение 1/W(p), обратное передаточной функции модели, можно разложить в ряд по степени р:
Коэффициенты a,b приведенных передаточных функций связаны с коэффициентами S следующей системой уравнений:
Коэффициенты Si связаны с переходной функцией h(t) соотношениями:

Соотношения (6) оптимальны для решения средствами Python при интерполяции h(t) кубическими сплайнами, что будет доказано на примерах.
Оценка адекватности математических моделей идентификации объектов управления
Для выбора оптимальной модели достаточно использовать показатель адекватности второго порядка:

где 


Лучшей следует считать модель, обеспечивающую максимальное значение
Учитывая существенную погрешность численного дифференцирования при решении системы уравнений (5), реализуем символьное дифференцирование. Для этого применим интерполяцию полиномом в соответствии со следующим листингом:
Время работы программы: 0.802
Высокая степень адекватности модели 0.99743 свидетельствует о том, что полученная передаточная функция:
достаточно точно отображает динамические свойства объекта.
Кривая разгона получена экспериментально, поэтому дельнейшие исследование систем управления объектом на устойчивость [4] и определения параметров регуляторов [5] приобретают практическое значение.
Реализация средствами Python задачи идентификации объекта модифицированным методом площадей
Для решения этой задачи можно использовать численные методы поскольку модель не содержит дифференцирования, а предложенный метод решения согласно соотношениям (6) не предполагает смены координаты времени. Кроме этого, применим интерполяцию сплайном в соответствии со следующим листингом:
Время работы программы: 0.238
Высокая степень адекватности модели 0.99996 и большее быстродействие, чем при символьном дифференцировании, позволяет утверждать, что передаточная функция:
полученная модернизированным методом площадей лучше отображает динамические свойства объекта.
Выводы
1. Публикация знакомит с основами динамической идентификации объекта управления.
2. Реализация решения задачи идентификации на свободно распространяемом языке программирования Python с примерами использования явного представления переходной функции полиномом и сплайнами будет способствовать расширению области применения Python.
3. Для численных решений задач идентификации, можно предложить использование соотношений (6), которые позволяют получить результат без изменения координаты времени.
Что означает идентификация математической модели
Определения и задачи идентификации математических моделей
Идентификация динамических объектов в общем случае состоит в определении их структуры и параметров по наблюдаемым данным входному воздействию и выходным величинам.
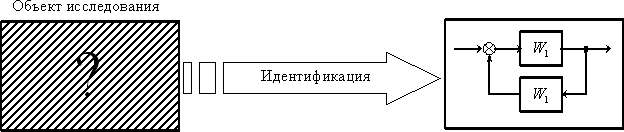
В этом случае объект (элемент системы, объект управления, элемент технологического процесса и т. п.) представляет собой «черный ящик». Исследователю необходимо, подвергая объект внешним воздействиям и анализируя его реакции, получить математическую модель (описание его структуры и параметров), то есть превратить «черный ящик» в «белый ящик», добиться его «информационной прозрачности». Графически процесс идентификации иллюстрирует рис. 1.
Важным моментом этого процесса является выбор точек приложения внешних воздействий и сбор информации о реакциях объекта, то есть размещение управляющих устройств и датчиковых систем.
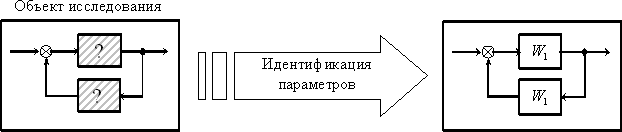
Решается при идентификации объектов и более простая (относительно простая) задача, это задача идентификации параметров, когда заранее известна структура математической модели объекта, но не известны ее параметры. В этом случае говорят о переходе от «серого ящика» к «белому ящику». Графически процесс идентификации параметров иллюстрирует рис. 2.
Задача идентификации параметров может либо входить компонентом в общую задачу идентификации объекта, либо решаться самостоятельно.
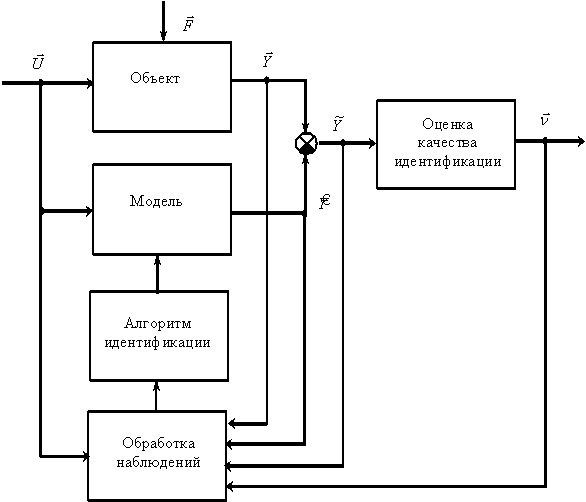
Рассмотрим на обобщенной структуре и процедуре процесса идентификации основы подхода к решению задач идентификации. Обобщенная структура процесса идентификации показана на рис. 3.
Обобщенная процедура идентификации
Выбор для определенного класса объекта настраиваемую модель, то есть модель, структуру и параметры которой можно менять в процессе идентификации.
Выбрать критерий (оценку) качества идентификации, характеризующий в виде функционала доступных для наблюдения переменных отличие модели и объекта.
Выбрать алгоритм идентификации (механизм настройки модели), обеспечивающий сходимость процесса идентификации, минимум критерия качества идентификации.
Методы идентификации принято разделять на две группы:
активная идентификация идентификация вне контура управления,
пассивная идентификация идентификация в контуре управления.
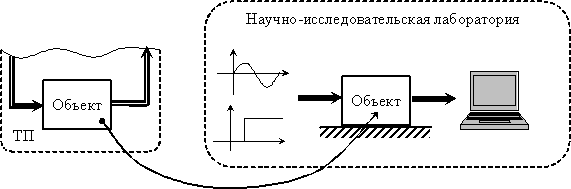
В этом случае объект исследования выводится из условий нормальной окружающей среды (нормальный режим эксплуатации, номинальные параметры рабочего режима и т. п.). Исследования проводятся в специализированных лабораторных условиях, как это показано на рис. 4. На входы объекта (рабочие и дополнительные) подаются тестовые сигналы специального вида. Это могут быть:
ступенчатые и импульсные временные сигналы,
случайные воздействия с заданными параметрами.
Активную идентификацию используют при разработке новых технологий применительно к действующим промышленным объектам, в изучении новых явлений, в первоначальной разработке математической модели.
При пассивной идентификации объект функционирует в контуре управления, находится в процессе нормальной эксплуатации. На его входы поступают только естественные сигналы управления.
Пассивную идентификацию используют для уточнения математической модели, для слежения за изменениями в объекте. Информация оперативно используется в системе управления объектом, процесс такой идентификации иллюстрируется рис. 5.
Кроме перечисленных групп методов реализуются и системы идентификации смешанного типа, когда объект не выводится из нормального режима эксплуатации, но к управляющим сигналам добавляются тестовые воздействия, позволяющие идентифицировать объект, не ухудшая качества основного процесса управления.
Более подробно рассмотрим активную идентификацию.
Активная идентификация объектов управления может производиться как во временной области, так и в частотной области. При этом В каждой области используют собственные алгоритмы и методы идентификации.
При активной идентификации в большинстве случаев используют полученные в результате экспериментов характеристики:
частотные характеристики (АФЧХ, ЛАЧХ, ЛФЧХ и др.),
временные характеристики (ступенчатое изменение задания, «узкий» импульс задания и др.).
Рассмотрим в качестве примера один из подходов решения задачи идентификации структуры и параметров объекта в частотной области. Ограничим рассмотрение объектом с одним входом и одним выходом.
Мы знаем, что если имеется математическая модель такого объекта в виде передаточной функции
то это соответствует наличию полной информации о структуре и параметрах объекта, всех его характеристиках.
Преобразуем передаточную функцию (1) к полюсно-нулевому представлению, форме Боде
где 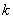

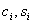
Если среди корней (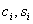
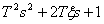
Предполагая для простоты изложения отсутствие комплексно сопряженных корней, можно преобразовать (2) к следующему виду
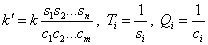
По выражению для передаточной функции в виде (3) получим частотную характеристику объекта
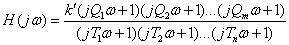
С другой стороны, нам известно, что ЛАЧХ и ЛФЧХ динамических звеньев с передаточными функциями
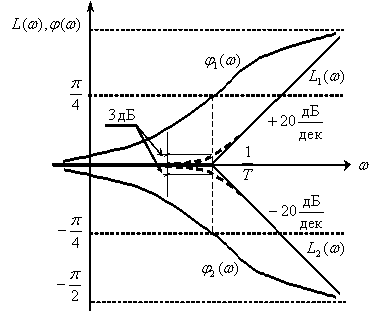
имеет вид, показанный на рис. 6, так как звенья являются соответственно форсирующим и апериодическим динамическими звеньями первого порядка.
Исходя из изложенного материала, можно предложить следующую процедуру активной идентификации структуры и параметров линейной системы с одним входом и одним выходом:
В процессе эксперимента с объекта снимается частотная характеристика в виде ЛАЧХ и ЛФЧХ.
Полученная экспериментально ЛАЧХ аппроксимируется кусочно-линейной криво1 набором отрезков (асимптот) с целочисленным наклоном кратным 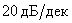
По наклону асимптот и частотам сопряжения асимптот определяется передаточная функция объекта в виде произведения передаточных функций соответствующих асимптотам элементарных динамических звеньев (апериодических и форсирующих).
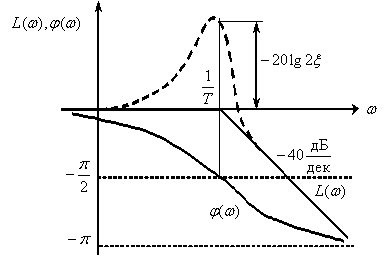
При наличии в полученной ЛАЧХ и ЛФЧХ признаков звеньев второго порядка, то есть асимптот с наклоном кратным 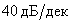
Колебательное звено с передаточной функцией
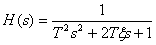
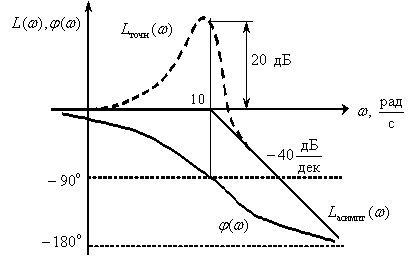
имеет ЛАЧХ и ЛФЧХ, показанные на рис. 7.
Форсирующее звено второго порядка с передаточной функцией
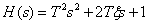
имеет ЛАЧХ (ЛФЧХ) симметричные показанным на рис. 7 характеристикам колебательного звена относительно оси частот.
Рассмотрим пример идентификации по рассмотренной процедуре.
По экспериментально полученной ЛАЧХ объекта определить передаточную функцию.
Аппроксимируем экспериментальную ЛАЧХ набором асимптот, как это показано на рис. 8.
Рассмотрим теперь участки аппроксимированной ЛАЧХ, на которых наклон не изменяется:
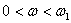
На этом интервале виду асимптоты соответствует ЛАЧХ интегрирующего звена, его передаточная функция

Этому звену соответствует следующее выражение ЛАЧХ
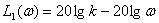
Используем последнее выражение для определение 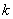

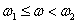
На этом интервале наклон асимптоты возрос на 20 дБ/дек, что соответствует добавлению апериодического звена первого порядка с передаточной функцией
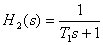
где постоянная времени определяется по точке сопряжения асимптот

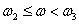
На этом интервале наклон асимптоты уменьшился на 20 дБ/дек, что соответствует добавлению форсирующего звена первого порядка с передаточной функцией
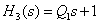
где постоянная времени определяется по точке сопряжения асимптот
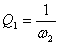
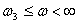
На этом интервале наклон асимптоты возрос на 20 дБ/дек, что соответствует добавлению апериодического звена первого порядка с передаточной функцией
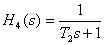
где постоянная времени определяется по точке сопряжения асимптот
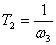
Перемножая полученные передаточные функции, получим передаточную функцию объекта
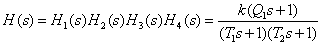
Контрольные вопросы и задачи
Дайте определение процессу идентификации объекта, идентификации параметров.
Какие методы относят к методам пассивной идентификации?
Какие методы относят к методам активной идентификации?
Поясните процедуру идентификации параметров объекта управления по его экспериментальной ЛАЧХ.
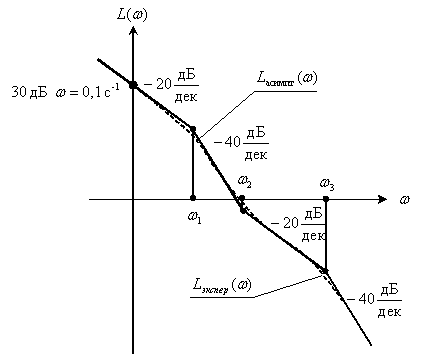
Асимптотическая ЛАЧХ объекта имеет вид
Определите передаточную функцию объекта.
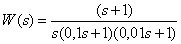
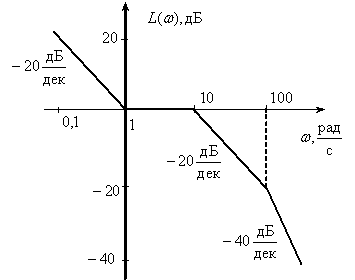
Асимптотическая ЛАЧХ объекта имеет вид
Определите передаточную функцию объекта.
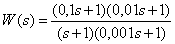
Асимптотическая и точная ЛАЧХ динамического звена имеет вид
Определите передаточную функцию звена.