Что означает математика с греческого
Презентация была опубликована 8 лет назад пользователемРоза Степурина
Похожие презентации
Презентация на тему: » Слово «математика» произошло от греческого (mathema), что означает изучение, знание, наука. Математика-царица наук. В математике изучаются числа и цифры;» — Транскрипт:
2 Слово «математика» произошло от греческого (mathema), что означает изучение, знание, наука. Математика-царица наук. В математике изучаются числа и цифры; меры длины, ширины, объёма, площади, массы; разные фигуры и знаки и т.д. Без математики не может существовать физики, химии, алгебры, геометрии и других наук.
3 Геометрия- в переводе с греческого «измерение земли»; раздел математики, изучающий фигуры: треугольники, квадраты, овалы, круги, ромбы и другие простые фигуры. Но есть и другие более сложные фигуры как например: пирамиды, кубы, параллелепипеды, сферы, полусферы, октаэдры, нонаэдры, додекаэдры, гексаэдры, гептаэдры, икосаэдры, икосододекаэдры, декаэдрические призмы, цилиндры и другие сложные фигуры которые изучаются в геометрии. Икосододекаэдр – это полуправильный многогранник, у которого 32 грани: 20 треугольников и 12 пятиугольников. Неправильная декаэдрическая призма – это торцевые грани призмы – многоугольники в виде звезды. У фигур которых много углов называют многоугольники.
8 Есть и меры длины, веса, скорости и другие меры. Меры длины – миллиметры, сантиметры, дециметры, метры, километры и другие. Меры веса – миллиграммы, граммы, центнеры, тонны и другие меры веса. Меры скорости – километры в час, километры в секунду, Метры в секунду, километры в час и другие меры скорости, их много. И других мер немало.
10 Архимед был великим учёным до нашей эры. Родился в 287г. до н.э.-212 г. до н.э. Умер в одном месте- Сиракузы. Архимед- Древнегреческий математик, физик и инженер из Сиракуз. Он сделал множество открытий. Много его открытий не сохранилось. Архимед открыл закон плавучести тел. Как вода полилась через край. Он смог посчитать может и неправильно, но смог вычислить диаметр солнца.
11 Пифагор родился приблизительно в 580г. До н.э. и умер около 500г. До н.э. Он был: древнегреческий философ, религиозный и политический деятель, основатель пифагореизма и математик. Пифагор учил медицине, принципам политической деятельности, астрономии, математике, музыке, этике и многому другому. Из его школы вышли выдающиеся политические и государственные деятели, историки, математики и астрономы.
Значение слова «математика»
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
матема́тика
1. наука, занимающаяся изучением чисел, геометрических фигур и тел, структур, пространств и преобразований ◆ Грамотку, которую мой всемилостивейший Государь ко мне писал о самом чюднейшем и чрезмеру редко бываемом человеке, господине Даниле Дмитревиче Новицком, что моему всемилостивейшему Государю возвещено о великом его учение, 〈…〉 что он по твоему, моего всемилостивейшего Государя, указу исполнил, и всё выучил, геометрию и математику, а аще и ни одной цыфири не знает, и что день и ночь над начертанием пушек и мортиров, и ныне хочет начать учиться пушки лить; но мне мнится, что столко же будет и столко же выучится, как и математику. Аника Щербаков, письмо Петру I о Д. Д. Новицком (22 июля 1699) // «Письма и бумаги императора Петра Великого», т. I (1688—1701), 1887 г. (цитата из библиотеки Google Книги)
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: приграничный — это что-то нейтральное, положительное или отрицательное?
Математика
Содержание
Основные сведения
Идеализированные свойства исследуемых объектов либо формулируются в виде аксиом, либо перечисляются в определении соответствующих математических объектов. Затем по строгим правилам логического вывода из этих свойств выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Таким образом первоначально, исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.
Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное с математикой положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе было предложено много различных определений математики (см. ниже).
Этимология
В текстах на русском языке слово «математика» или «мафематика» встречается по крайней мере с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год) [5]
Определения
Одно из первых определений предмета математики дал Декарт [6] :
К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики.
Математика… наука о количественных отношениях и пространственных формах действительного мира.
Это определение Энгельса [8] ; правда, далее Колмогоров поясняет, что все использованные термины надо понимать в самом расширенном и абстрактном смысле.
Сущность математики… представляется теперь как учение об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств,— именно тех, которые в качестве аксиом положены в основание теории… Математика есть набор абстрактных форм — математических структур.
Приведём ещё несколько современных определений.
Герман Вейль пессимистически оценил возможность дать общепринятое определение предмета математики:
Вопрос об основаниях математики и о том, что представляет собой в конечном счёте математика, остаётся открытым. Мы не знаем какого-то направления, которое позволит в конце концов найти окончательный ответ на этот вопрос, и можно ли вообще ожидать, что подобный «окончательный» ответ будет когда-нибудь получен и признан всеми математиками.
Разделы математики
1. Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе и образованную дисциплинами:
и высшую математику, изучаемую на нематематических специальностях вузов. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности.
Программа обучения по специальности математика [13] образована следующими учебными дисциплинами:
2. Математика как специальность научных работников Министерством образования и науки Российской Федерации [14] подразделяется на специальности:
3. Для систематизации научных работ используется раздел «Математика» [15] универсальной десятичной классификации (УДК).
4. Американское математическое общество (AMS) выработало свой стандарт для классификации разделов математики. Он называется Mathematics Subject Classification. Этот стандарт периодически обновляется. Текущая версия — это MSC 2010. Предыдущая версия — MSC 2000.
Обозначения
Вследствие того, что математика работает с чрезвычайно разнообразными и довольно сложными структурами, система обозначений также очень сложна. Современная система записи формул сформировалась на основе европейской алгебраической традиции, а также математического анализа (понятия функции, производной и т. д.). Геометрия испокон века пользовалась наглядным (геометрическим же) представлением. В современной математике распространены также сложные графические системы записи (например, коммутативные диаграммы), нередко также применяются обозначения на основе графов.
Краткая история
Академиком А. Н. Колмогоровым предложена такая структура истории математики:
Развитие математики началось вместе с тем, как человек стал использовать абстракции сколько-нибудь высокого уровня. Простая абстракция — числа; осмысление того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, года. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.
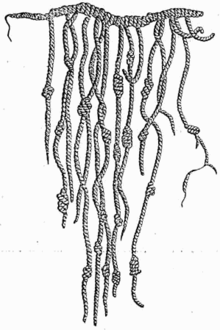
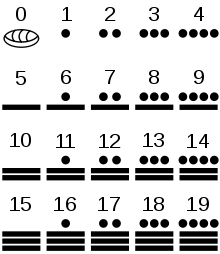
Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления. Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами Среднего царства. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля.
Исторически основные математические дисциплины появились под воздействием необходимости вести расчёты в коммерческой сфере, при измерении земель и для предсказания астрономических явлений и, позже, для решения новых физических задач. Каждая из этих сфер играет большую роль в широком развитии математики, заключающемся в изучении структур, пространств и изменений.
Философия математики
Цели и методы
Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного раздела математики — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.
Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.
Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. «Пространство 

Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.
Основания
Вопрос сущности и оснований математики обсуждался со времён Платона. Начиная с XX века наблюдается сравнительное согласие в вопросе, что надлежит считать строгим математическим доказательством, однако отсутствует согласие в понимании того, что в математике считать изначально истинным. Отсюда вытекают разногласия как в вопросах аксиоматики и взаимосвязи отраслей математики, так и в выборе логических систем, которыми следует при доказательствах пользоваться.
Помимо скептического, известны нижеперечисленные подходы к данному вопросу.
Теоретико-множественный подход
Предлагается рассматривать все математические объекты в рамках теории множеств, чаще всего с аксиоматикой Цермело — Френкеля (хотя существует множество других, равносильных ей). Данный подход считается с середины XX века преобладающим, однако в действительности большинство математических работ не ставят задач перевести свои утверждения строго на язык теории множеств, а оперируют понятиями и фактами, установленными в некоторых областях математики. Таким образом, если в теории множеств будет обнаружено противоречие, это не повлечёт за собой обесценивание большинства результатов.
Логицизм
Данный подход предполагает строгую типизацию математических объектов. Многие парадоксы, избегаемые в теории множеств лишь путём специальных уловок, оказываются невозможными в принципе.
Формализм
Данный подход предполагает изучение формальных систем на основе классической логики.
Интуиционизм
Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства (но, как считается, и более надёжную). Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств — бессмысленными (неформализуемыми).
Конструктивная математика
Основные темы
Числа
Понятие «число» первоначально относилось к натуральным числам. В дальнейшем оно было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.
| |||||||||||||||
 |  | ||||||||||||||
| Комплексные числа | Кватернионы | ||||||||||||||
 Числовые системы Числовые системы | |
|---|---|
| Счётные множества | Натуральные числа ( ) • Целые ( ) • Целые ( ) • Рациональные ( ) • Рациональные ( ) • Алгебраические ( ) • Алгебраические ( ) • Периоды • Вычислимые • Арифметические ) • Периоды • Вычислимые • Арифметические |
| Вещественные числа и их расширения | Вещественные ( ) • Комплексные ( ) • Комплексные ( ) • Кватернионы ( ) • Кватернионы ( ) • Числа Кэли (октавы, октонионы) ( ) • Числа Кэли (октавы, октонионы) ( ) • Седенионы ( ) • Седенионы ( ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) |
| Другие числовые системы | Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа |
| См. также | Двойные числа • Иррациональные числа • Трансцендентные • Числовой луч • Бикватернион |
Преобразования
 | 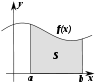 |  |  |
| Арифметика | Дифференциальное и интегральное исчисление | Векторный анализ | Анализ |
 |  |  | |
| Дифференциальные уравнения | Динамические системы | Теория хаоса |
Структуры
Пространственные отношения
Более наглядные подходы в математике.
Дискретная математика
Дискретная математика включает средства, которые применяются над объектами, способными принимать только отдельные, не непрерывные значения.
 |  |  |  |
| Математическая логика | Теория вычислимости | Криптография | Теория графов |
Коды в системах классификации знаний
Онлайновые сервисы
Существует большое число сайтов, предоставляющих сервис для математических расчётов. Большинство из них англоязычные. [20] Из русскоязычных можно отметить сервис математических запросов поисковой системы Nigma.
Что означает математика с греческого
ПРОИСХОЖДЕНИЕ МАТЕМАТИЧЕСКИХ СЛОВ И ЗНАКОВ
Математика. Слово математика пришло к нам из древнегреческого, где означало « учиться», «приобретать знания». И не прав тот, кто говорит: «Мне не нужна математика, я ведь не собираюсь стать математиком». Математика нужна всем. Раскрывая удивительный мир окружающих нас чисел, она учит мыслить яснее и последовательнее, развивает мысль, внимание, воспитывает настойчивость и волю. говорил: «Математика ум в порядок приводит». Одним словом, математика учит нас учиться приобретать знания.
Здесь уместно поговорить о математических терминах и символах. От арабского слова ifr ( «ноль») ведёт происхождение слово « цифра». Первое достоверное свидетельство о записи ноля относится к 876 г.; в настенной надписи из Гвалиора ( Индия) имеется число 270. Некоторые исследователи предполагают, что ноль быль заимствован у греков, которые ввели в качестве ноля букву « о» в шестидесятиричную систему счисления, употребляемую ими в астрономии. Другие, наоборот, считают, что ноль пришёл в Индию с востока, он был изобретён на границе индийской и китайской культур. Обнаружены более ранние надписи от 683 и 686 гг. в нынешних Камбодже и Индонезии, где нуль изображён в виде точки и малого кружка.
Знаки « » и «-» впервые встречаются у немецкого математика Видмана в 1489 г.; возникновение этих знаков неясно. Наверное, они возникли в торговой практике. Первой печатной книгой, содержащей изложение приемов вычислений с применением знаков « » и «-», является руководство немецкого математика Г. Грамматеуса ( 1518). Позже их употребляли М. Штифель ( 1545), А. Ризе ( 1550). В других странах содействовали введению этих символов руководства английских математиков Рекорда ( 1557), Оутрида ( 1631), Гарриота ( 1631) и французских математиков Рамуса ( 1555), Виета ( 1579).
Знак умножения « х» ввел Оутрид ( 1631). Точка в качестве знака умножения появляется у немецкого математика Региомонтана ( XV в.), затем у Гарриота ( 1631), и, наконец, уже у Лейбница ( 1698), который подчеркивал значение точки как знака умножения.
Горизонтальная черточка в качестве знака деления впервые встречается у итальянского математика Леонардо Пизанского ( XIII в.), известного также под именем Фибоначчи. Знак деления « :» впервые встречается у английского математика Джоса ( 1633), затем у Лейбница ( 1684).
Знак равенства « » введен Рекордом ( 1557). Знаки неравенств « » и «» предложены Гарриотом ( 1631).
Круглые скобки появляются у итальянского математика Тартальи ( 1556). Фигурные скобки употребляет Виет ( 1593). Степени а2, а3, …, аn вводит французский математик и философ Декарт ( 1637). Корни — Рудольф ( 1525) и голландский математик Жирар ( 1629). Следует отметить, что если знаки « » и «» были сразу приняты, так как в типографиях была латинская литера V, то другие математические знаки вошли во всеобщее употребление гораздо позже их введения.
Запятая в записи дробей впервые встречается в 1592 г., а в 1617 г. шотландский математик Джон Непер предложил отделять десятичные знаки от целого числа либо запятой, либо точкой.
Современную запись, отделение целой части запятой, предложил Кеплер ( 1571 — 1630).
В странах, где говорят по-английски ( Англия, США, Канада и др.), и сейчас вместо запятой пишут точку, например: 2.3 и читают: два точка три.
Знак « %» происходит, как полагают, от итальянского слова cento ( сtо), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буква t превратилась в наклонную черту ( /), возник современный символ для обозначения процента pro cento-cento-cto-c/o-%
ИЗ ИСТОРИИ МАТЕМАТИЧЕСКИХ ТЕРМИНОВ
«ЛИНИЯ» происходит от латинского слова « линеа» — льняная ( имеется в виду льняная нить). От этого же корня происходит наше слово линолеум, первоначально означавшее льняное полотно.
КВАДРАТ произошел от латинского слова « кваттуор» ( четыре) — фигура с четырьмя сторонами.
РОМБ происходит от латинского слова « ромбус», означающего бубен. Мы привыкли к тому, что бубен имеет круглую форму, но раньше бубны имели форму квадрата или ромба, о чем свидетельствуют изображения « бубен» на игральных картах.
ТРАПЕЦИЯ происходит от латинского слова « трапезиум» — столик. От этого же слова происходит наше слово « трапеза», означающее стол.
ДИАГОНАЛЬ происходит от греческого « диа», что означает « через» и «гония» — угол, рассекающая углы, проходящая через углы.
КОНУС — это латинская форма греческого слова « конос», что означает сосновую шишку.
ЦИЛИНДР происходит от латинского слова « цилиндрус», означающего « валик», «каток».
ПРИЗМА — латинская форма греческого слова « присма» — опиленная ( имелось в виду опиленное бревно).
ПИРАМИДА — латинская форма греческого слова « пюрамис», которым греки называли египетские пирамиды; это слово происходит от древнеегипетского слова « пурама», которым эти пирамиды называли сами египтяне. Рассмотрим истоки слова и термина « пирамида». Сразу стоит отметить что « пирамида» или « pyramid» ( английский), «piramide» ( французский, испанский и славянские языки), «pyramide» ( немецкий) — это западный термин, берущий свой исток в древней Греции. В древнегреческом ( «пирамис» и мн. ч. «пирамидес») имеет несколько значений. Древние греки именовали « пирамис» пшеничный пирог, который напоминал форму египетских сооружений. Позже это слово стало означать « монументальную структуру с квадратной площадью в основании и с наклонными сторонам, встречающимися на вершине». Происхождение греческого слова имеет собственную историю. По одной из версий греки заимствовали это слово из Египта, где есть схожее по звучанию « Pir E Mit», означающее « часть числа» или « составляющая часть совершенства», но не пирамиду, как сооружение. Этимологический словарь указывает, что греческое « пирамис» происходит из египетского « pimar».
Из греческого слово перешло в латинский язык и вплоть до 16 века не трансформировалось в европейских языках, поскольку в средневековой Европе о пирамидах в Египте знали лишь образованные люди, говорящие на латыни. Первое письменное толкование слова « пирамида» встречается в Европе в 1555 г. и означает: «один из видов древних сооружений королей». После открытия пирамид в Мексике и с развитием наук в 18 веке, пирамида стала не просто древним памятников архитектуры, но и правильной геометрической фигурой с четырьмя симметричными сторонами ( 1716 г.).
СФЕРА — латинская форма греческого слова « сфайр» — мяч.
ТОЧКА — лат. «пункт» — пунктир; «пунктум» — укол, медицинский термин « пункция» — прокол.
Термин « параллелограмм» греческого происхождения и, согласно Проклу, был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам.
КОРЕНЬ — ( квадратный или корень уравнения) пришло от арабов. Арабские ученые представляли себе квадрат числа, вырастающий из корня — как растение, и потому называли корнями.
АЛГЕБРА. Математическая наука, объектом изучения которой являются алгебраические системы, например группы, кольца, поля и др. Отдельной ветвью алгебры является элементарная алгебра. Первый учебник алгебры — «Краткая книга об исчислении ал-Джабра и ал-Мукабалы» был написан в 825 г. арабским ученым ал-Хорезми. Слово ал-джабр при этом означало операцию переноса вычитаемых из одной части в другую и его буквальный смысл — «восполнение». Этот термин стал названием науки. В Европе такое название употреблялось уже в самом начале XIII в., но еще Ньютон называл алгебру « Общей арифметикой» ( 1707). Книга ал-Хорезми имеет особое значение в истории математики как руководство, по которому долгое время обучалась вся Европа. Именно под влиянием арабской математики алгебра сформировалась как учение о решении уравнений.
Слово « хорда» происходит от греческого слова « хорде» — «кишка», «струна» ( в древней Греции струны выделывались из воловьих кишок). И в Древней Греции, и в александрийской школе это слово не связывалось с хордой. И Евклид, и Птолемей, и другие александрийские ученые называли хорду « прямой в круге», имея в виду прямолинейный отрезок, вписанный в круг ( треугольник, вписанный в круг, они также называли « треугольником в круге»).
АКСИОМА. Термин впервые встречается у Аристотеля и перешел в математику от философов древней Греции. В переводе с греческого слово означает « достоинство», «уважение», «авторитет». Первоначально термин имел смысл « самоочевидная истина». В современном понимании аксиома — высказывание некоторой теории, принимаемое при построении этой теории без доказательства, принимаемое как исходное, отправное для доказательств других положений этой теории ( теорем). Аксиомы называют также постулатами.
ГЕОМЕТРИЯ ( греч. geometria, от ge — Земля и metreo — мерю), раздел математики, изучающий пространственные отношения и формы, а также другие отношений и формы, сходные с пространственными по своей структуре. Происхождение термина « Геометрия», что буквально означает « землемерие», можно объяснить следующими словами, приписываемыми древнегреческому учёному Евдему Родосскому ( 4 в. до н. э.): «Геометрия была открыта египтянами и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития р. Нил, постоянно смывавшего границы». Уже у древних греков Геометрия означала математическую науку, в то время как для науки об измерении Земли был введён термин геодезия. Судя по сохранившимся отрывкам древнеегипетских сочинений, геометрия развилась не только из измерений Земли, но также из измерений объёмов и поверхностей при земляных и строительных работах Первоначальные понятия Геометрия возникли в результате отвлечения от всяких свойств и отношений тел, кроме взаимного расположения и величины. Первые выражаются в прикосновении или прилегании тел друг к другу, в том, что одно тело есть часть другого, в расположении « между», «внутри». Вторые выражаются в понятиях « больше», «меньше», в понятии о равенстве тел.