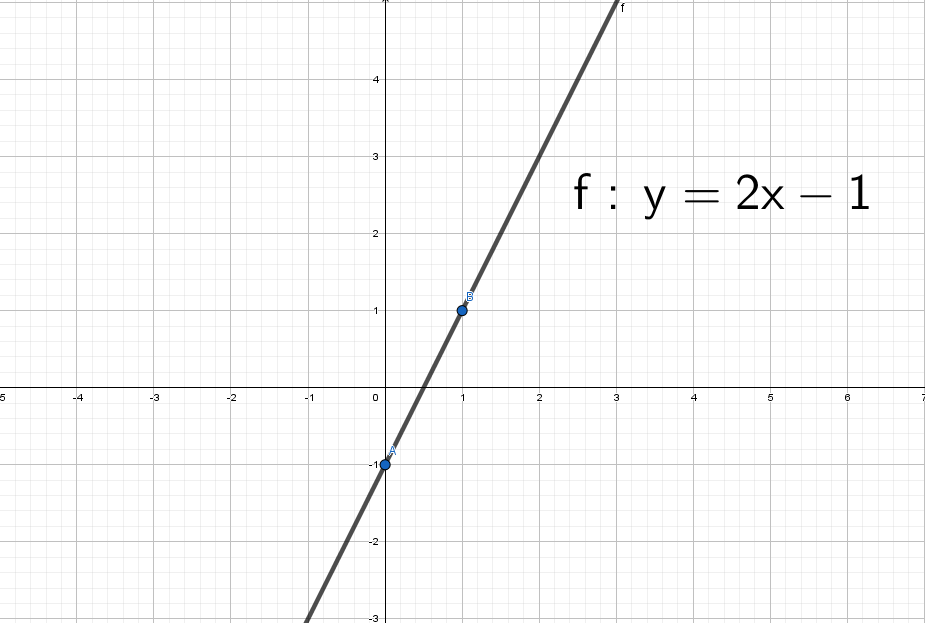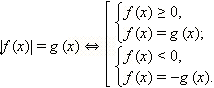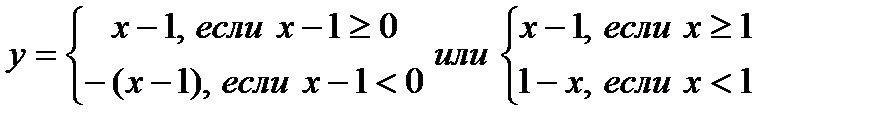Что означает модуль в графиках функций
Построение графиков с модулем
путём преобразований
Модуль аргумента и модуль функции
Если Вы попали на эту страницу из поисковика, миновав предыдущие разделы темы «Графики функций и их преобразования», то рекомендую сначала повторить графики основных элементарных функций и общие правила преобразования графиков функций.
В контексте построения графиков это означает использование преобразования симметрии относительно осей координат.
Пример 1.
Пример 2.
Один из способов быстро и точно построить исходную параболу по характерным точкам показан в видео на канале Mathematichka.
III При построении из графика функции y = f(x) более сложных графиков, например, вида y = k·f (a|x| + b) + c или y = k·|f (ax + b)| + c тщательно соблюдайте последовательность преобразований.
Пример 3.
Заметим, что x 2 = |x| 2 (значение четной степени, как и значение модуля, всегда неотрицательно). Поэтому, выделяя полный квадрат, преобразуем функцию к виду |y| = (|x| − 1) 2 − 6 и строим её график последовательными преобразованиями.
Строим график функции f(x) = (x − 1) 2 − 6 переносом на 1 вправо вдоль оси Ox, а затем переносом вниз на 6 единиц вдоль оси Oy.
Строим график функции f(|x|) = (|x| − 1) 2 − 6 с использованием преобразования симметрии относительно оси Oy.
Строим линии, удовлетворяющие уравнению |y| = (|x| − 1) 2 − 6 с использованием преобразования симметрии относительно оси Ox.
- 1.
 2.
2. 3.
3. 4.
4.
5.
 6.
6.
| 1.y = x 2 | 2.y = (x − 1) 2 | 3.y = (x − 1) 2 − 6 | 4.y = (|x| − 1) 2 − 6 |
| 5.y = (|x| − 1) 2 − 6, y ≥ 0 | 6.|y| = (|x| − 1) 2 − 6 |
Следующий график постройте самостоятельно, чтобы убедиться, что вы правильно поняли материал.
Пример 4.
Сумма модулей
Если формула функции включает сумму или разность несколько модулей, то следует разбить координатную плоскость на участки и построить каждую ветвь графика отдельно. Границы участков определяются приравниванием каждого модуля к нулю и решением соответствующего уравнения. Подробный пример такого подхода можно увидеть в задаче 1 на странице, посвященной решению уравнений с параметрами.
Однако, если подмодульные выражения простые и содержат элементарные функции, графики которых вам хорошо известны, то можно получить результат прямым сложением ординат этих графиков в характерных точках.
Пример 5.
Эти два модуля содержат только линейные функции, графиками которых являются прямые линии. В результате сложения должна получиться ломаная линия, состоящая из трёх звеньев. (2 модуля, следовательно 2 уравнения, каждое из которых имеет одно решение, следовательно 2 границы, которыми плоскость разбита на 3 участка.) Трёхзвенную ломаную можно построить по 4-ём точкам.
Теперь проверьте себя.
Пример 6.
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте ссылки.
Графики функций, содержащих переменную под знаком модуля. Обобщающее повторение при подготовке к экзамену
Разделы: Математика
Определение модуля
Алгебрагическое определение: | x | =
Геометрическое определение: модулем числа называется расстояние от точки, изображающей это число, до начала отсчета.
Понятие модуля впервые вводится в 6 классе, в 7 классе рассматривается линейная функция и ее график и уже можно показывать построение несложных графиков функций, содержащих модуль. Далее, по мере изучения различных функций, их свойств, каждую такую тему можно заканчивать рассмотрением более сложных графиков, в том числе с модулем. В этой статье рассматриваются основные приемы построения графиков таких функций.
I. На алгебрагическом определении основан метод «раскрытия модуля на промежутках».
Например: | x + 2 | = 
у = 
Если модулей несколько, то каждый из них раскрываем на промежутках относительно точек, обращающих каждый из них в нуль. Например, построим график функции у = | 3 – x | – x + | x + 2 | + 1.

у =
Подобно тому, как числовая прямая точками – 2 и 3 разбивается на промежутки, координатная плоскость прямыми х = – 2 и х = 3 разбивается на части («полосы»), в каждой из которых строим свой график. Заметим, что данная функция непрерывна, поэтому на «границах» части графика должны соединяться.

Например, построим график функции у = | log2 x – 1 | – log0,5 x.
Построим сначала график функции у = х 2 – 2х – 3. Графиком этой функции является парабола, ветви которой направлены вверх. Координаты ее вершины: х = 1, у = – 4. Точки пересечения параболы с осями координат: (0; – 3); (– 1; 0); (3; 0). Далее выполняем отображение части графика, лежащей в нижней полуплоскости, относительно оси абсцисс.
2) у = f(| x |). Используем определение модуля: f(| x |) =
Чтобы построить график такой функции строим график функции у = f(x) и берем ту его часть, где х > 0 (в правой полуплоскости). Затем эту часть симметрично отображаем в левую полуплоскость, где х 2 – 2| х | – 3. Сначала строим график функции у = х 2 – 2х – 3, далее выполняем указанные преобразования.
3) Построим график функции y = | f(| x |)|, например, y = | x 2 – 2| х | – 3 |, выполним последовательно преобразования, рассмотренные в пунктах 2 и 1.
4. Рассмотрим зависимость | y | = f(x). Ее нельзя назвать функцией, так как не выполняется условие: каждому значению х должно соответствовать единственное значение у.
Рассмотрим построение графика такой зависимости (можно говорить «графика уравнения»). Используем определение модуля: у = f(x), если у > 0, – у = f(x), y = – f(x), если у 0; чтобы построить график в нижней полуплоскости (где у 2 – 2х – 3
Заметим, что графики, не относящиеся к рассмотренным частным случаям, следует строить « раскрывая модули на промежутках».
IV. Приведем некоторые примеры
1. Построим график уравнения | y | = arccos| x |.
2. Графическим способом можно решать и неравенства с двумя переменными. Например, решением неравенства | y | 2 – 4 | x | + 3 |; y = 
2. Решите графически уравнения c одной и двумя переменными: | 3 – x | – 3 = 2| x | – x 2 ; | y | = 2| x | – x 2 ; 
3. Решите графически неравенства с двумя переменными: | y | > x 2 4x + 3; | x | + | y | 15.11.2011
Что такое модуль действительного числа
В данной публикации мы рассмотрим определение, геометрическую интерпретацию, график функции и примеры модуля положительного/отрицательного числа и нуля.
Определение модуля числа
Модуль действительного числа (иногда называется абсолютной величиной) – это величина, равная ему же, если число положительное или равная противоположному, если оно отрицательное.
Модуль числа a обозначается вертикальными черточками с обеих сторон от него – |a|.
Противоположное число отличается от исходного знаком. Например, для числа 5 противоположным является -5. При этом ноль является противоположным самому себе, т.е.
Геометрическая интерпретация модуля
Модуль числа a – это расстояние от начала координат (O) до точки A на координатной оси, которая соответствует числу a, т.е.
График функции с модулем
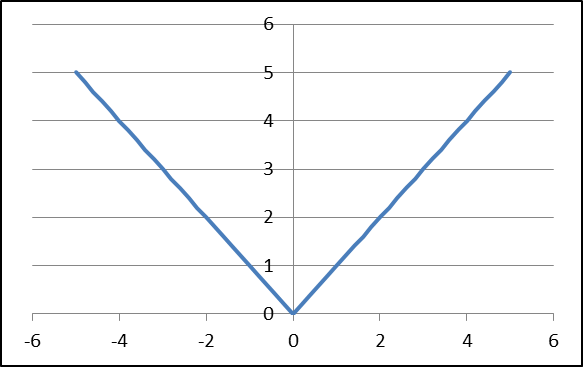
График четной функции y = |х| выглядит следующим образом:
Чему равняются следующие модули |3|, |-7|, |12,4| и |-0,87|.
Решение:
Согласно приведенному выше определению:
Графики прямой, параболы, гиперболы, с модулем
Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
Для понимания друг друга введу немного «обзываний» системы координат:
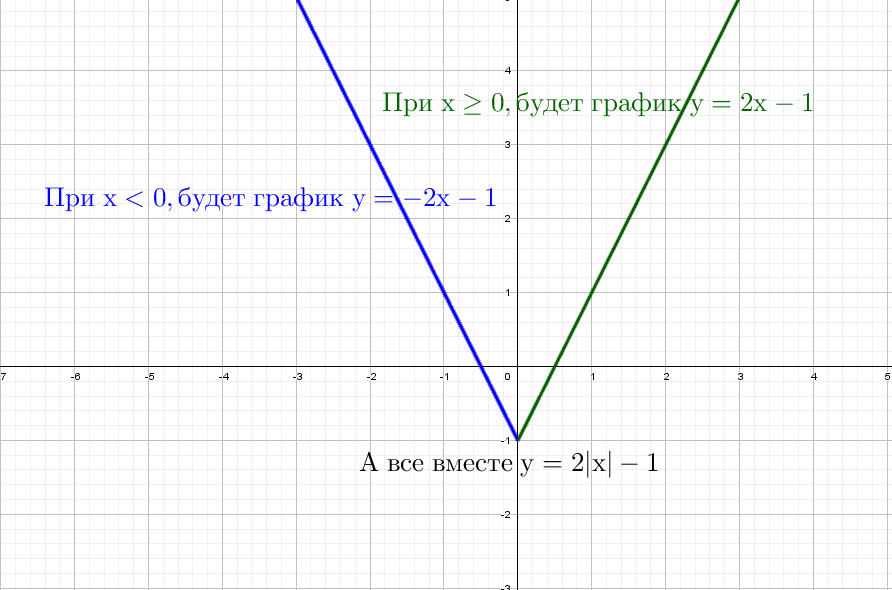
Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.
Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1
Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:
А если теперь добавить модуль y = |2x − 1|.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).
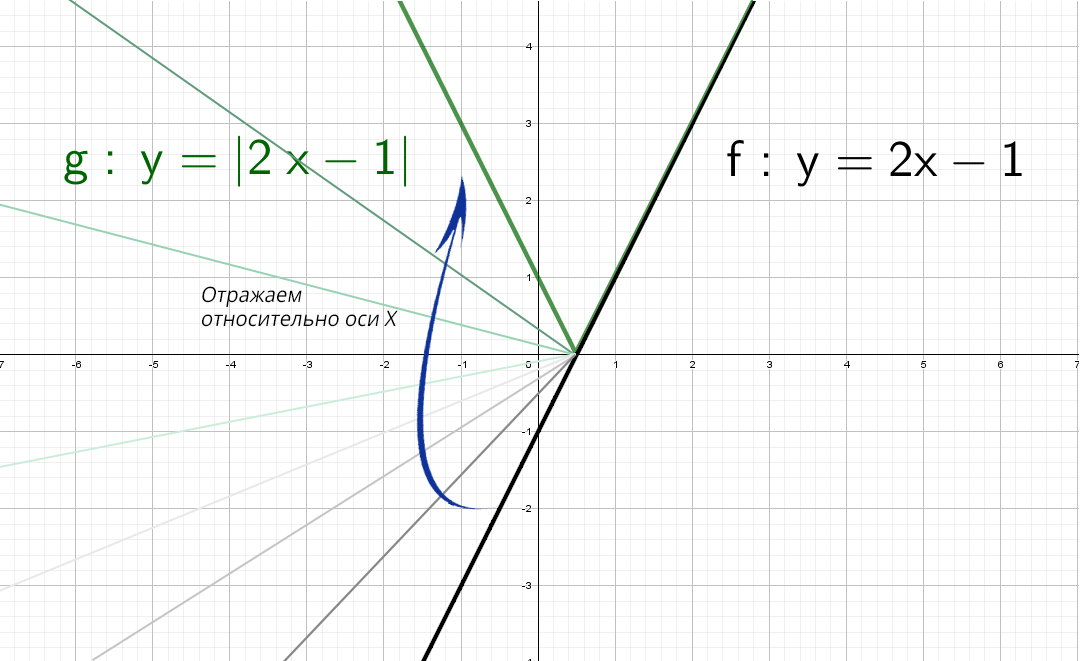
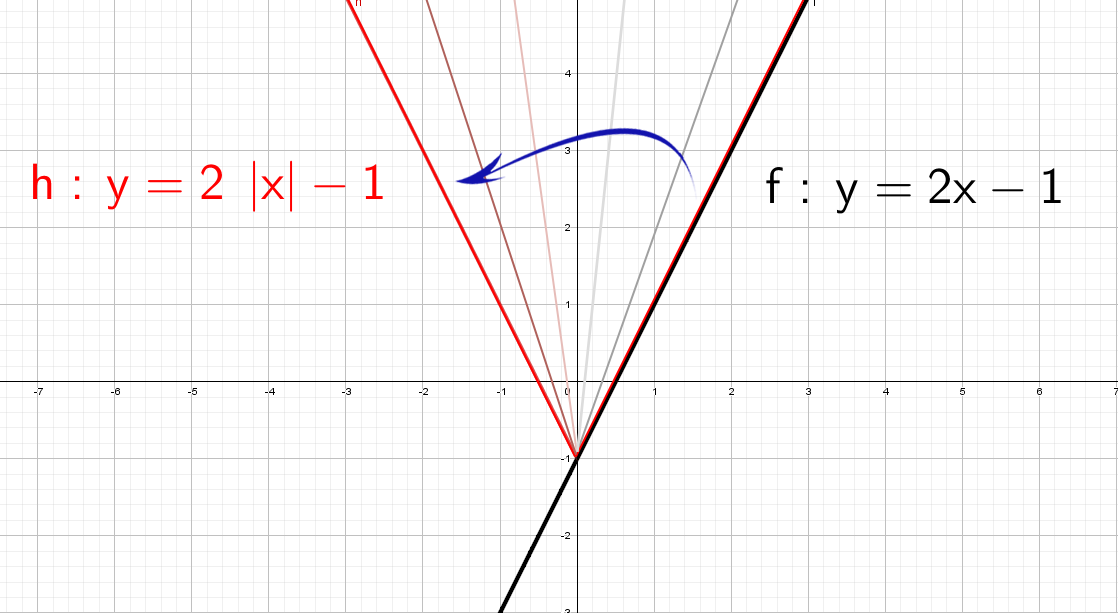
Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
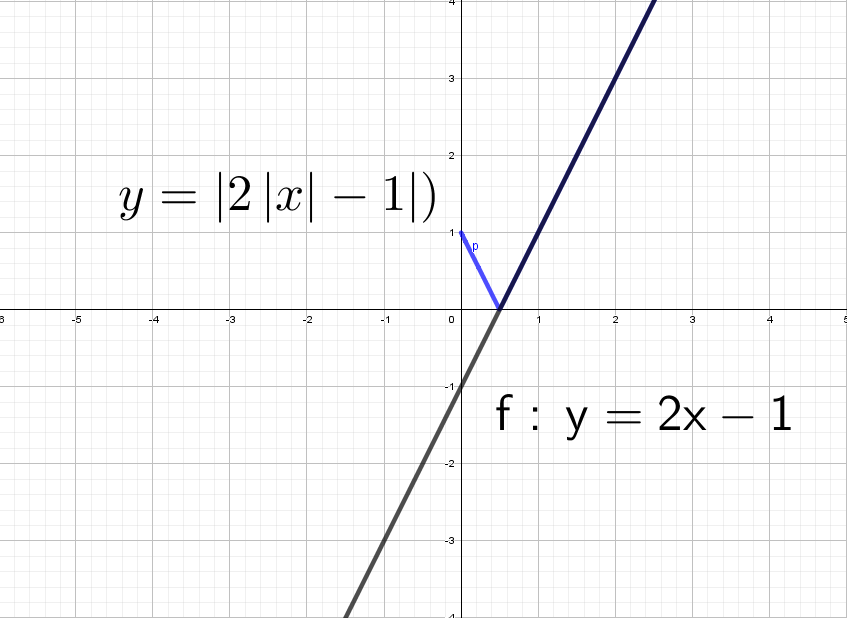
Смертельный номер: y = |2|x| − 1|.
Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.
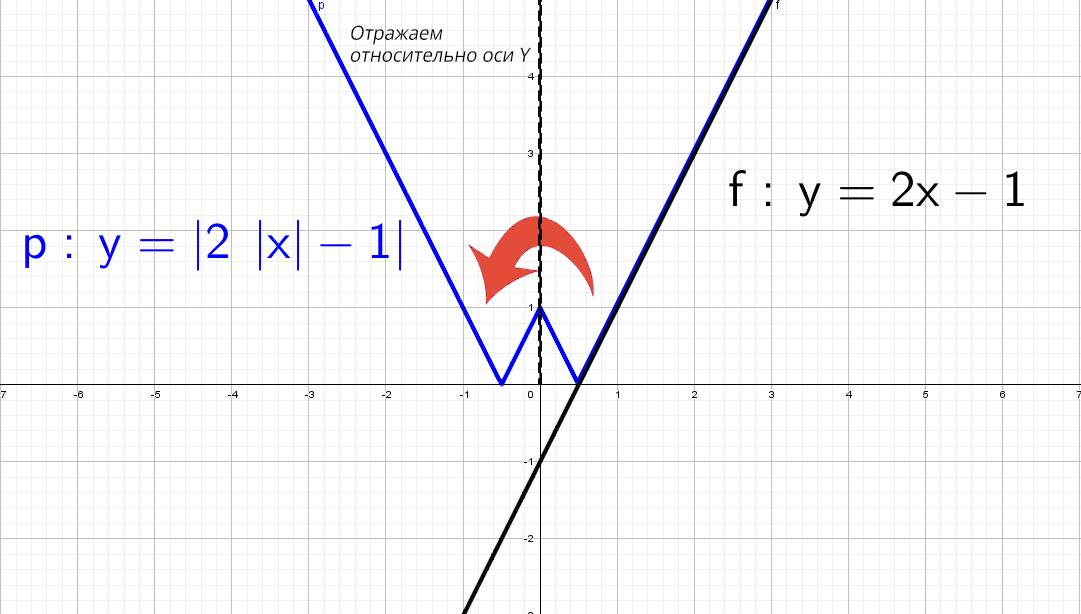
В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!
А после этого отражаем относительно оси «y» то, что мы получили справа налево:
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.
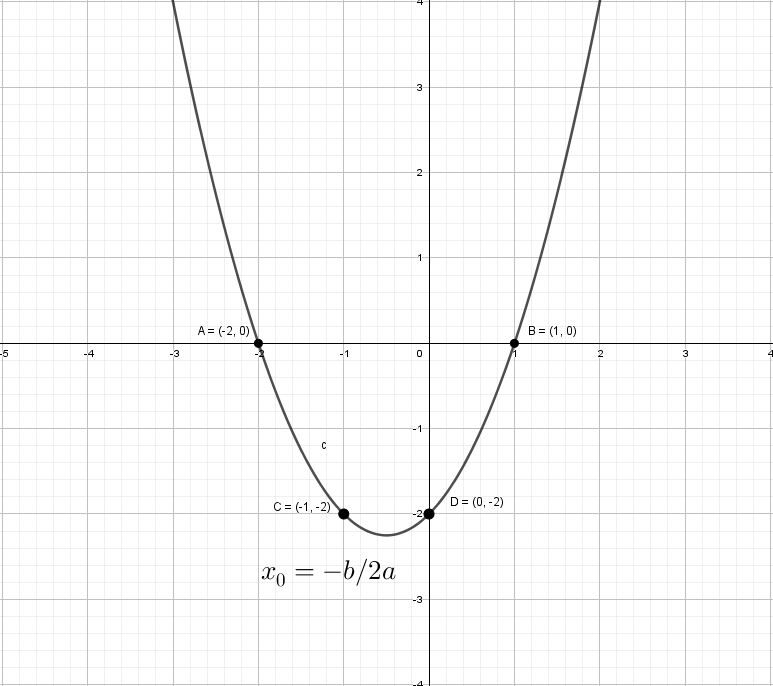
Можно найти вершину у параболы и взять пару точек для точного построения.
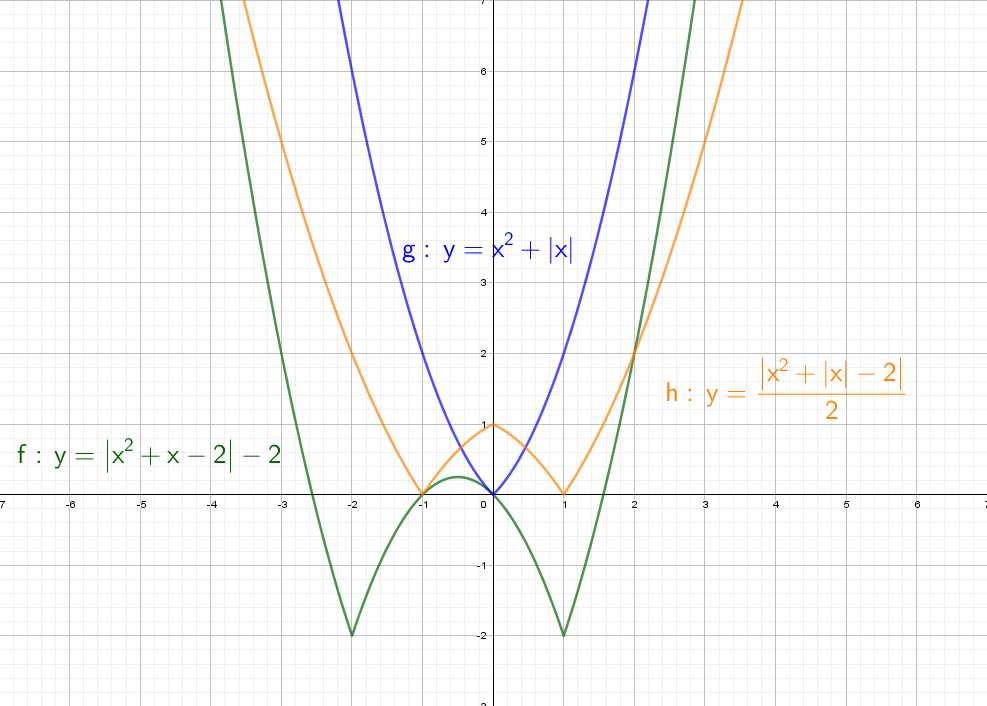
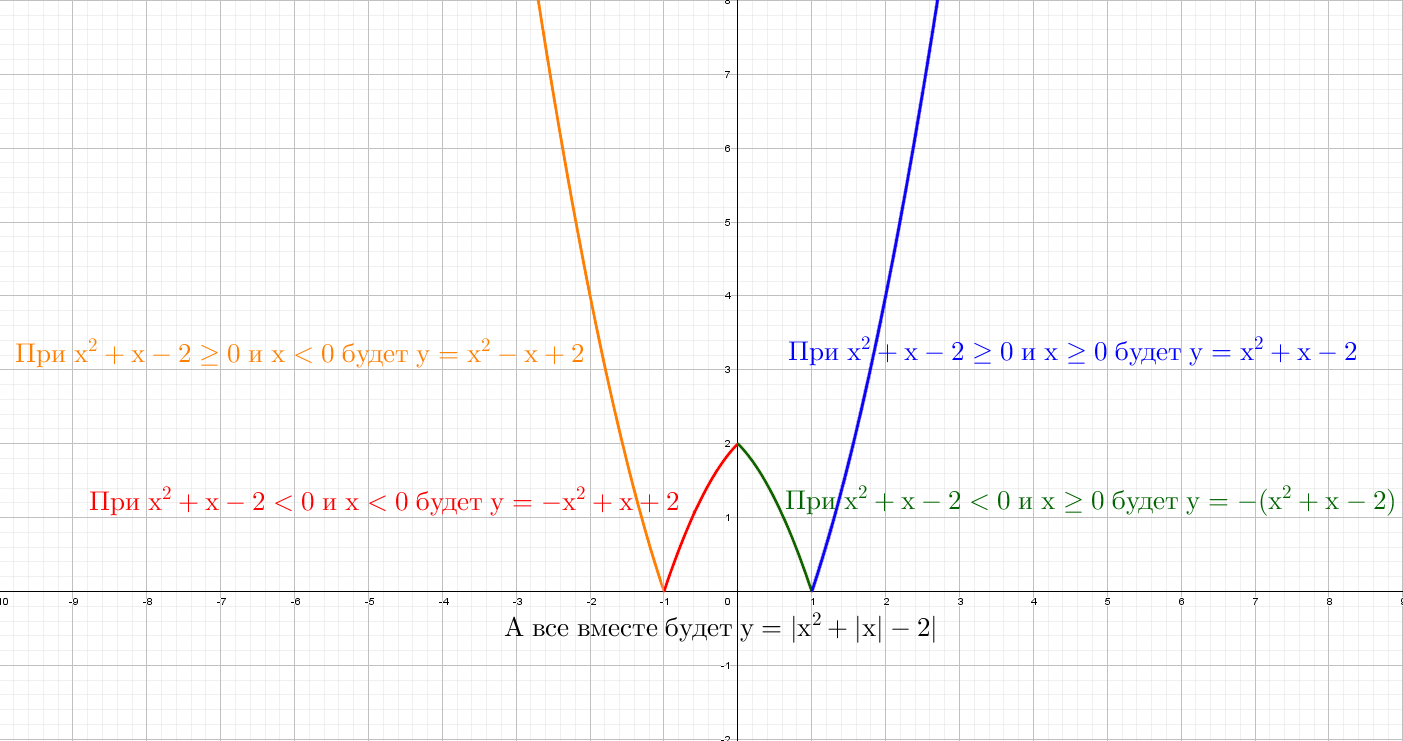
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
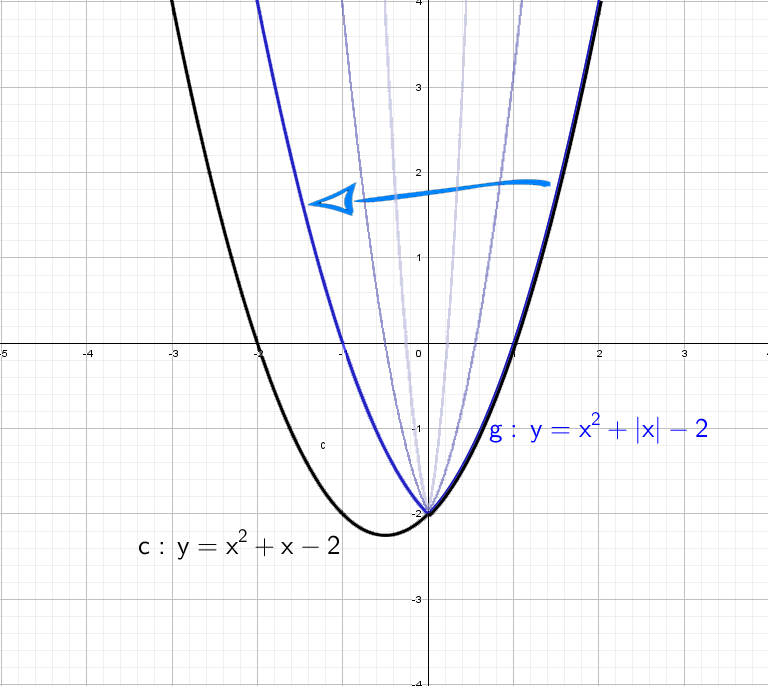
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
А дальше что мелочиться: рассмотри сразу остальные графики с модулем!
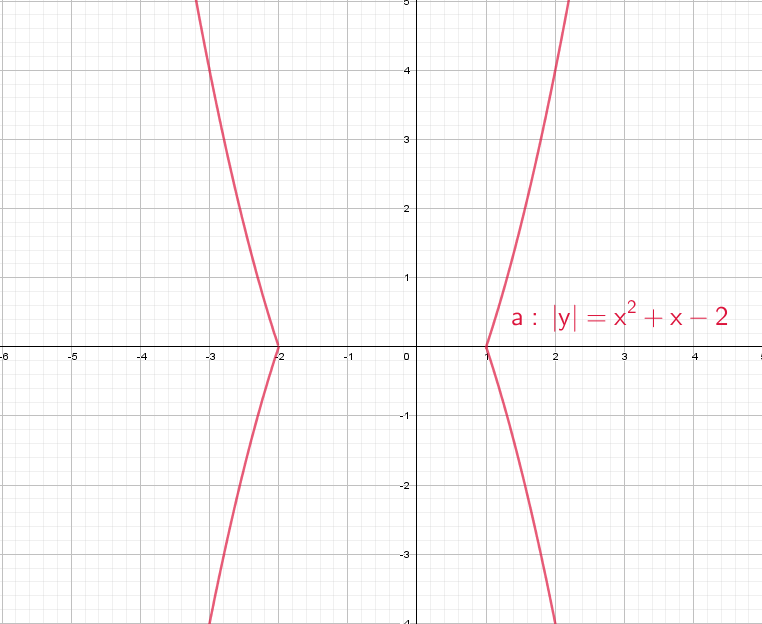
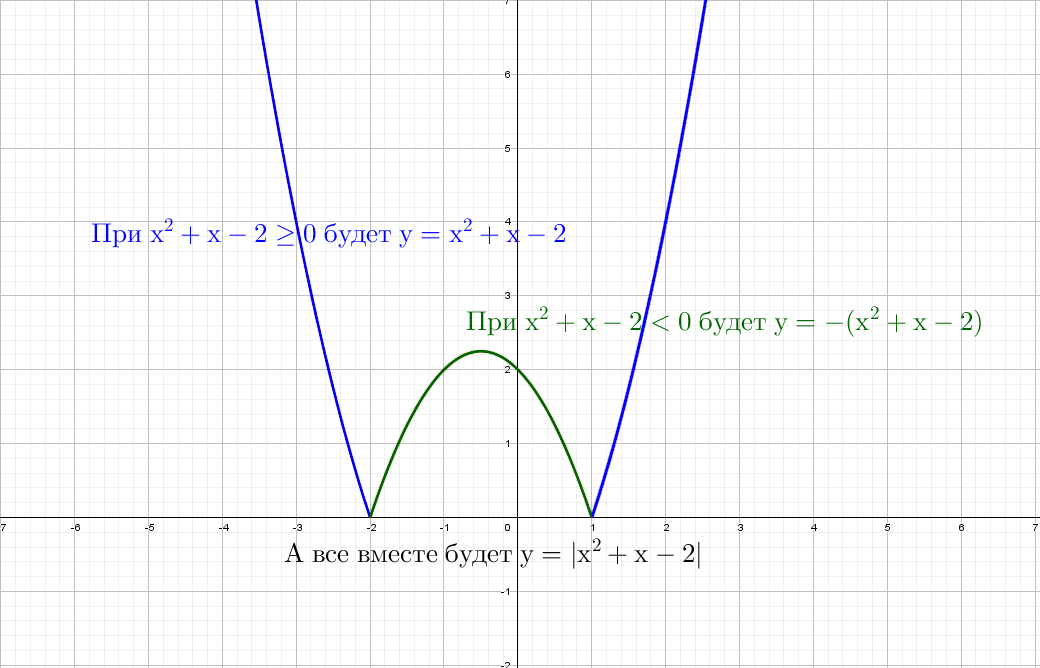
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
А теперь сразу комбо:
Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.
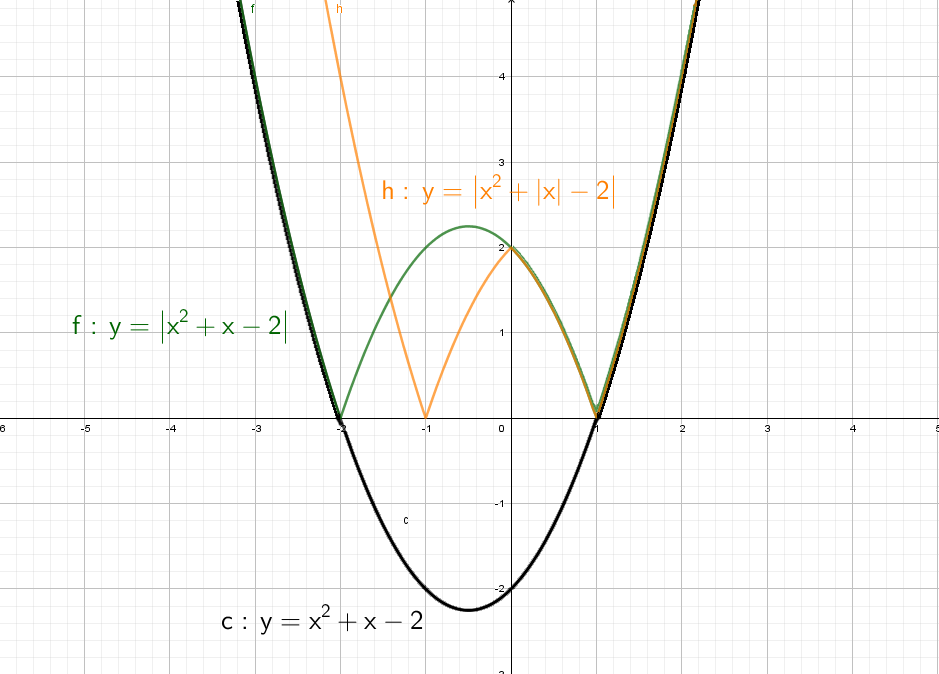
Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.
Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.
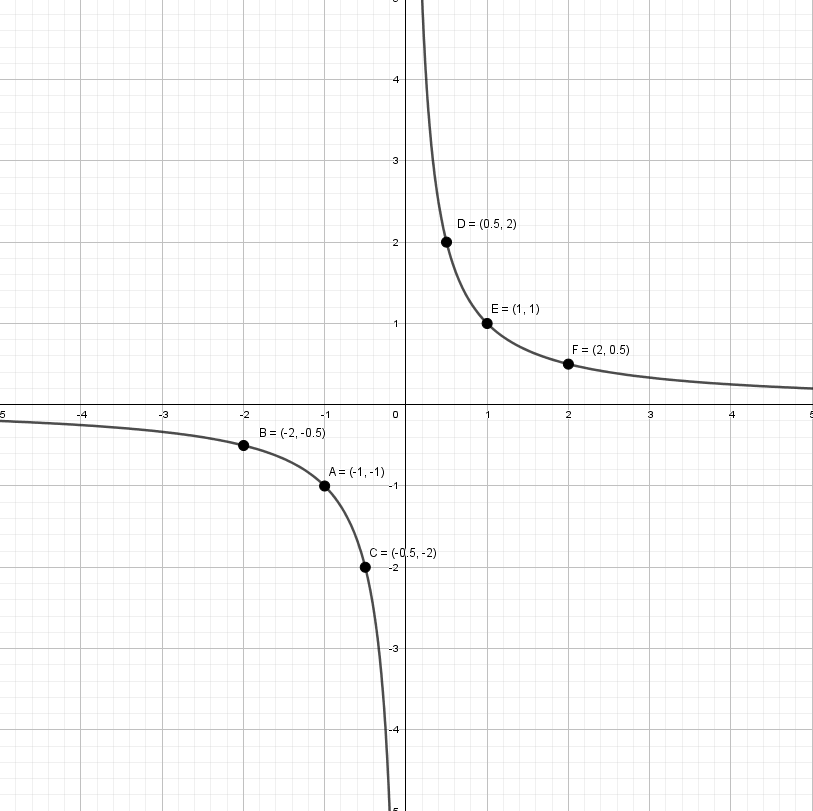
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
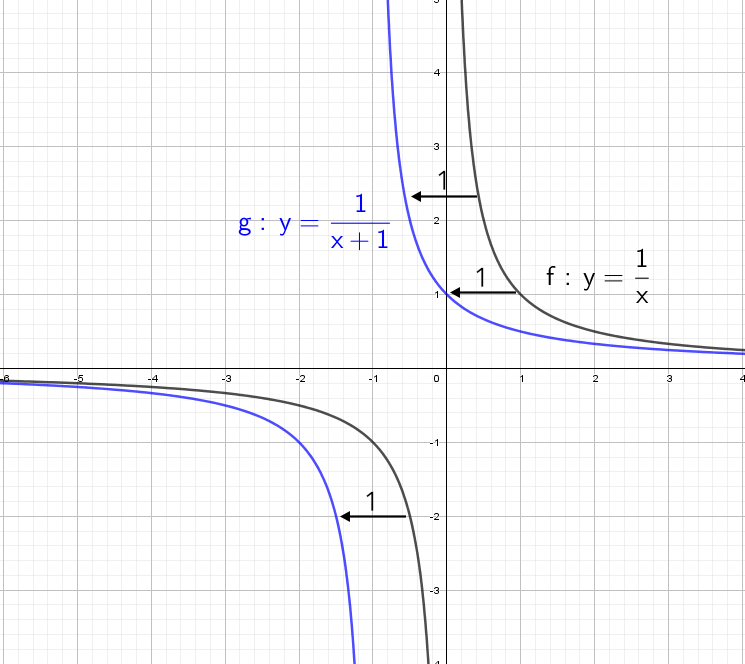
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
А что будет, если мы добавим в знаменателе « − 1»? График сдвинется вправо на единицу.
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!
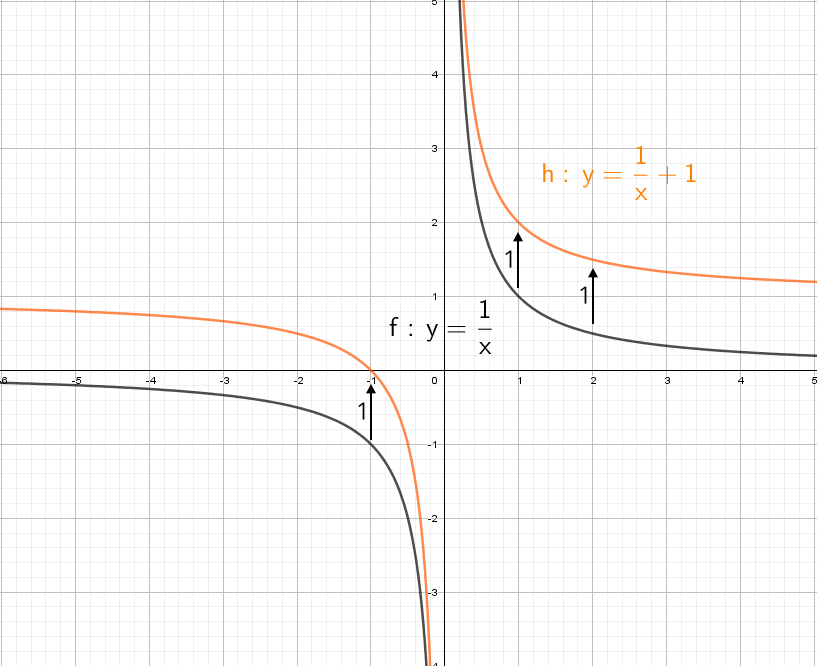
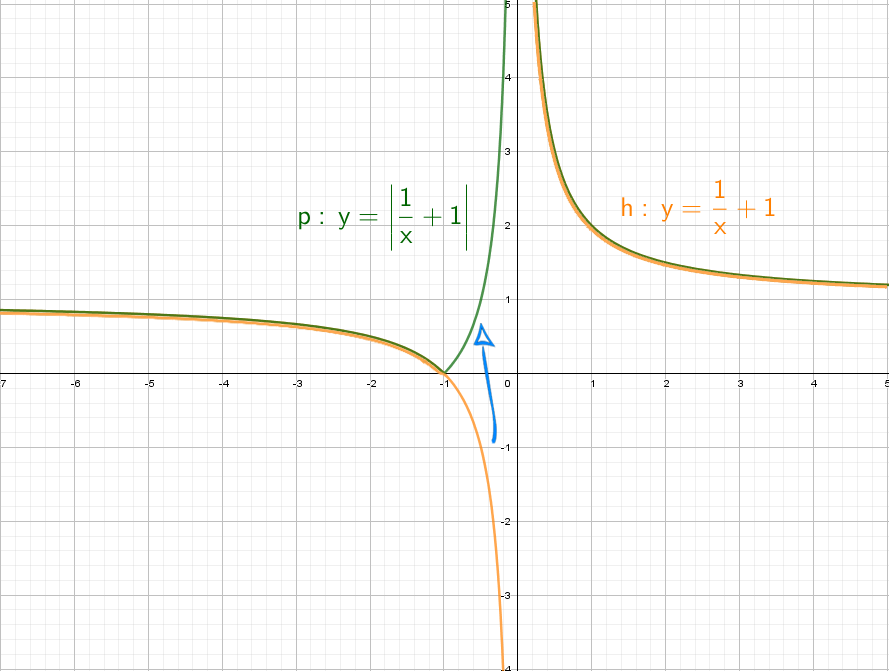
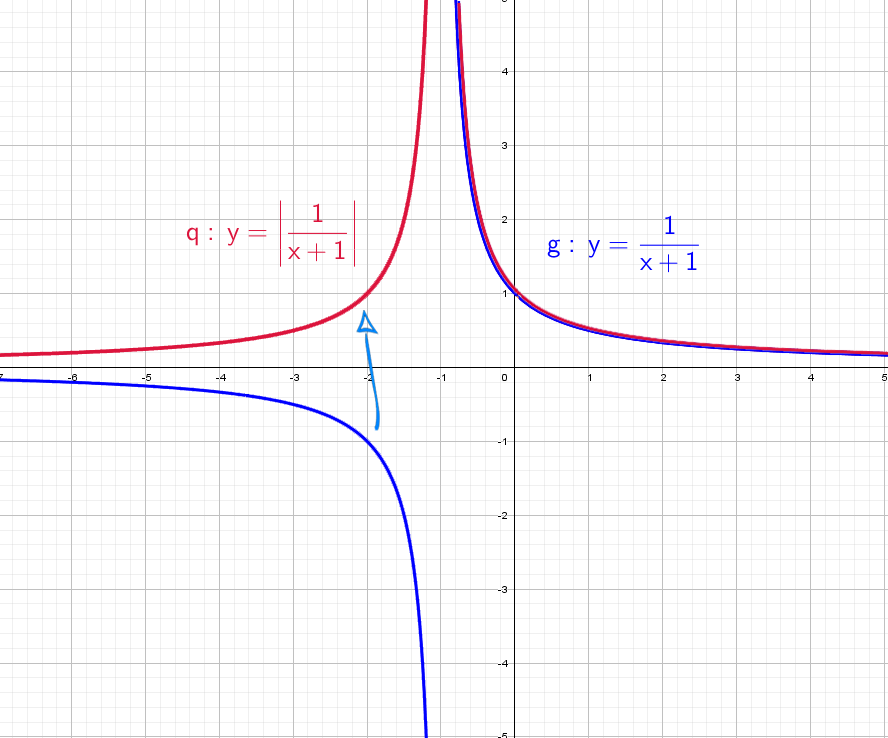
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.
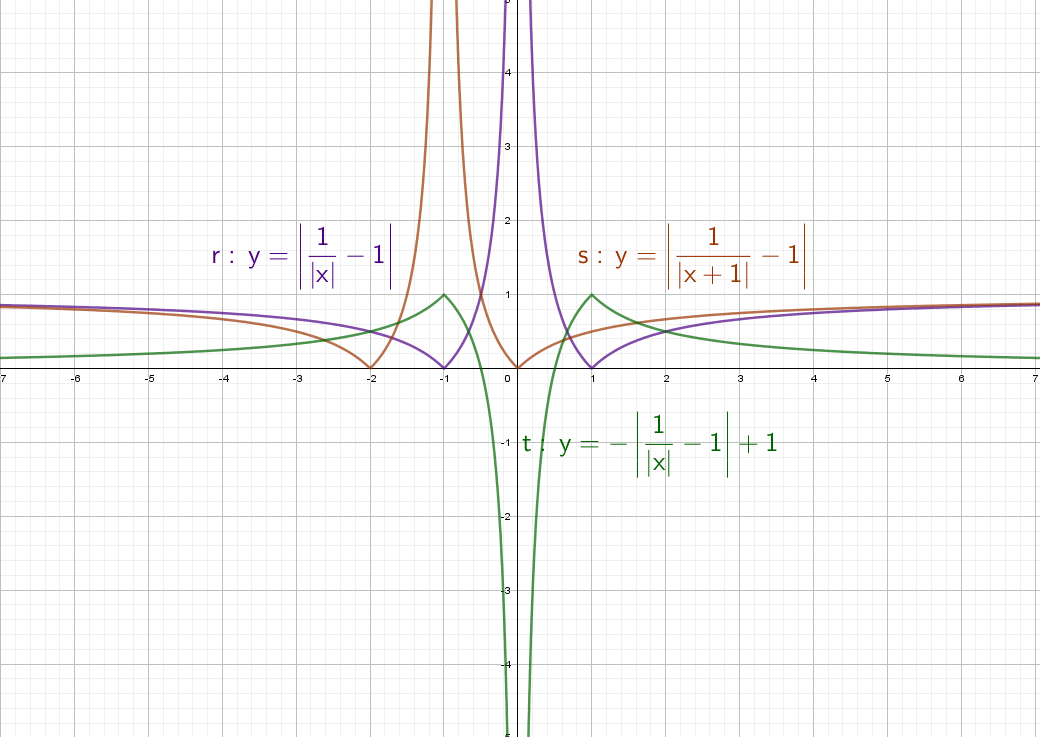
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.
Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.
Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:
Для параболы с одним модулем будет два кусочно-заданных графика:
C двумя модулями кусочно-заданных графиков будет четыре:
Свойство модуля. Построение графика функции «Модуль». Свойства функции



Если рассматривать геометрический смысл модуля, то говорят, что модуль – расстояние до конкретной точки координатной прямой от начала координат в единичных отрезках. Так как никакое расстояние не может быть отрицательным, то легко понять, что значение модуля любого числа – это число неотрицательное. Например, расстояние от начала координат до точки А(-5) равно 5. По-другому, |-5|=5.
Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчёта, т.е. удалена от начала координат на 0 единичных отрезков. Для положительного числа и нуля модуль равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули: |-а|=|а|.
Итак, 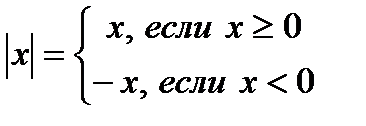
Свойства модулей чисел: 1) |а|≥0; 2) |ab|=|a|⸳|b|; 3) 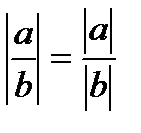
Решим уравнение |x-1|=2, используя определение и смысл модуля.
|-2|=2 и |2|=2. Т.е. х-1= –2 или х-1=2. Получили 2 линейных уравнения. Корнем уравнения х-1= –2 является число х= –1, а корнем уравнения х-1=2 является число х=3.
Проверим решения. |-1-1|=|-2|=2, |3-1|=|2|=2.
Перейдём к построению графика функции у= |х|. Вспомним алгоритм построения графика функции:
1) находим область определения функции;
2) берём несколько точек из области определения функции;
3) подставляем значения х из ООФ в уравнение функции;
4) полученные пары чисел (х;у) – точки графика функции.
Областью определения функции «Модуль» является вся числовая ось. Для построения графика возьмём 3 или 5 точек. 1 точка – вершина графика, 2 или 4 точки – для более точного построения.
| х | -2 | -1 | 0 | 1 | 2 |
| у | 2 | 1 | 0 | 1 | 2 |
Построим график функции у=|х-1|. Так как в формулу функции входит модуль, то его необходимо раскрыть, рассмотрев 2 случая. Поэтому функцию можно записать в виде
То есть при х≥1 строится луч, удовлетворяющий уравнению х-1, а при х
Рассмотрим неравенство |х|≤а, где а>0. Этому неравенству удовлетворяют все точки х, находящиеся на расстоянии, не большем а, от точки 0, т.е. точки отрезка [-a;a].