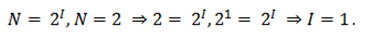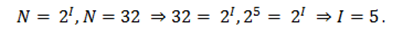Что означает n в формуле хартли

Что означает n в формуле хартли

1.2. Формула Хартли измерения количества информации. Закон аддитивности информации

Как уже упоминалось выше, в качестве основной единицы измерения информации мы будем использовать бит. Соответственно, с точки зрения алфавитного подхода мы будем кодировать информацию при помощи нулей и единиц (двоичных знаков).

Для того чтобы измерить количество информации в сообщении, надо закодировать сообщение в виде последовательности нулей и единиц наиболее рациональным способом, позволяющим получить самую короткую последовательность. Длина полученной последовательности нулей и единиц и является мерой количества информации в битах.

Поставим себе одну из наиболее часто встречающихся задач в теории информации. Пусть у нас есть `N` возможных равновероятных вариантов исходов некоторого события. Какое количество информации нам нужно получить, чтобы оставить только один вариант?

Например, пусть мы знаем, что некоторая интересная для нас книга находится на одной из полок нашего книжного шкафа, в котором `8` полок. Какое количество информации нам нужно получить, чтобы однозначно узнать полку, на которой находится книга?

Решим эту задачу с точки зрения содержательного и алфавитного подходов. Поскольку изначально в шкафу было `8` полок, а в итоге мы выберем одну, следовательно, неопределённость знания о местоположении книги уменьшится в `8` раз. Мы говорили, что один бит – это количество информации, уменьшающее неопределённость знания в `2` раза. Следовательно, мы должны получить `3` бита информации.

Теперь попробуем использовать алфавитный подход. Закодируем номера всех полок при помощи `0` и `1`. Получим следующие номера: `000, 001, 010, 011, 100, 101, 110, 111`. Для того чтобы узнать, на какой полке находится книга, мы должны узнать номер этой полки. Каждый номер состоит из `3` двоичных знаков. А по определению, `1` бит (в алфавитном подходе) – это количество информации в сообщении, состоящем из `1` двоичного знака. То есть мы тоже получим `3` бита информации.

Прежде чем продолжить рассмотрение поставленной общей задачи введём важное математическое определение.

Назовём логарифмом числа `N` по основанию `a` такое число `X`, что Обозначение:

На параметры логарифма налагаются некоторые ограничения. Число `N` обязательно должно быть строго больше `0`. Число `a` (основание логарифма) должно быть также строго больше нуля и при этом не равняться единице (ибо при возведении единицы в любую степень получается единица).

Теперь вернёмся к нашей задаче. Итак, какое же количество информации нам нужно получить, чтобы выбрать один исход из `N` равновероятных? Ответ на этот вопрос даёт формула Хартли: `H=log_aN`, где `N` – это количество исходов, а `H` – количество информации, которое нужно получить для однозначного выбора `1` исхода. Основание логарифма обозначает единицу измерения количества информации. То есть если мы будем измерять количество информации в битах, то логарифм нужно брать по основанию `2`, а если основной единицей измерения станет трит, то, соответственно, логарифм берётся по основанию `3`.

Рассмотрим несколько примеров применения формулы Хартли.

В библиотеке `16` стеллажей, в каждом стеллаже `8` полок. Какое количество информации несёт сообщение о том, что нужная книга находится на четвёртой полке?

Решим эту задачу с точки зрения содержательного подхода. В переданном нам сообщении указан только номер полки, но не указан номер стеллажа. Таким образом, устранилась неопределённость, связанная с полкой, а стеллаж, на котором находится книга, мы всё ещё не знаем. Так как известно, что в каждом стеллаже по `8` полок, следовательно, неопределённость уменьшилась в `8` раз. Следовательно, количество информации можно вычислить по формуле Хартли `H=log_2 8=3` бита информации.

Имеется `27` монет, одна из которых фальшивая и легче всех остальных. Сколько потребуется взвешиваний на двухчашечных весах, чтобы однозначно найти фальшивую монету?

В этой задаче неудобно использовать бит в качестве основной единицы измерения информации. Двухчашечные весы могут принимать три положения: левая чаша перевесила, значит, фальшивая монета находится в правой; правая чаша перевесила, значит, монета находится в левой; или же весы оказались в равновесии, что означает отсутствие фальшивой монеты на весах. Таким образом, одно взвешивание может уменьшить неопределённость в три раза, следовательно, будем использовать в качестве основной единицы измерения количес-тва информации трит.

По формуле Хартли `H = log _3 27 = 3` трита. Таким образом, мы видим, что для того чтобы найти фальшивую монету среди остальных, нам потребуется три взвешивания.

Логарифмы обладают очень важным свойством: `log_a(X*Y)=log_aX+log_aY`.

Если переформулировать это свойство в терминах количества информации, то мы получим закон аддитивности информации: Коли-чество информации`H(x_1, x_2)`, необходимое для установления пары `(x_1, x_2)`, равно сумме количеств информации `H(x_1)` и `H(x_2)`, необходимых для независимого установления элементов `x_1` и `x_2`:

Проиллюстрируем этот закон на примере. Пусть у нас есть игральная кость в форме октаэдра (с `8` гранями) и монета. И мы одновременно подбрасываем их вверх. Нужно узнать, какое количество информации несёт сообщение о верхней стороне монеты после падения (орёл или решка) и числе, выпавшему на игральной кости.

Игральная кость может упасть `8` различными способами, следовательно, по формуле Хартли можно вычислить, что, определив число, выпавшее на игральной кости, мы получаем `3` бита информации. Соответственно, монета может упасть только `2` способами и несёт в себе `1` бит информации. По закону аддитивности информации мы можем сложить полученные результаты и узнать, что интересующее нас сообщение несёт `4` бита информации.

Если в результате вычислений по формуле Хартли получилось нецелое число, а в задаче требуется указать целое число бит, то результат следует округлить в большую сторону.

Источник

Алфавитный подход к оценке количества информации. Формула Хартли

Вы будете перенаправлены на Автор24

Содержательный подход к оценке количества информации, который мы рассматривали ранее, измеряет ее количество, как уменьшение неопределенности наших знаний.

Однако любое техническое устройство не способно воспринимать непосредственно содержание информации, оно лишь понимает наличие или отсутствие электрических сигналов. Вследствие чего в вычислительной технике вынуждены использовать другой подход к оценке количества информации, который называется алфавитным.

Принцип алфавитного подхода к оценке количества информации

Алфавитный подход строится на принципе, утверждающем, что любое сообщение можно представить в виде кодов с помощью конечной последовательности символов, содержащейся в любом алфавите. Носители информации содержат любые последовательности символов, которые могут храниться, передаваться и обрабатываться как с помощью человека, так и с помощью технических устройств, в частности компьютера. Этот подход описал А.Н. Колмогоров, согласно которому, информативность, заключающаяся в последовательности символов, не может зависеть от содержания самого сообщения, а может определяться лишь минимальным количеством символов, необходимых для ее кодирования. Подобный подход к оценке количества информации носит объективный характер, так как не зависит от получателя, принимающего сообщения. Смысл же сообщений может учитываться только на этапе выбора алфавита кодирования либо не учитываться совсем.

В основу принципа этого подхода лег подсчет числа символов в сообщении, таким образом, важна только длина сообщения и совсем не учитывается его содержание. Однако на длину сообщения может влиять мощность алфавита используемого языка.

Мощность алфавита и информационная емкость. Формула Хартли

Все множество символов, из которых состоит язык, можно традиционно назвать алфавитом. Как правило, под алфавитом понимаются только буквы, но кроме них при написании текстов используются знаки препинания, цифры, скобки, пробелы, их тоже, в свою очередь, можно включить в алфавит.

Например:

Готовые работы на аналогичную тему

При алфавитном подходе считают, что каждый символ текста несет в себе определенную информационную емкость, которая, в свою очередь, зависит от мощности алфавита.

Хартли утверждал, что на количество информации, содержащейся в сообщении, может влиять фактор неожиданности, который, в свою очередь, зависит от вероятности получения сообщения. Если эта вероятность получения сообщения высокая, а неожиданность при этом низкая, то сообщение будет содержать мало полезной для человека информации.

Однако при создании своей формулы Р.Хартли полностью исключил фактор неожиданности. Формула Хартли работает только в том случае, когда появление символов равновероятно и они статистически независимы.

Например, с помощью приведенной формулы можно определить количество информации, которое несет знак в двоичной системе счисления:

Информационная емкость знака двоичной системы составляет 1 бит.

Необходимо определить информационную емкость буквы русского алфавита (без учета буквы «ё»).

Решение:

Представим себе, что текст к нам поступает последовательно, по одному знаку, словно бумажная лента, выползающая из телеграфного аппарата. Предположим, что каждый символ, который появляется на ленте, с равной вероятностью может быть любым символом алфавита. В действительности это не совсем так, но для упрощения примем такое предположение.

Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.

Количество информации в сообщении можно определить, используя формулу:

Рассмотрим пример решения задачи

Решение. Чтобы решить задачу, для начала определим количество знаков в сообщении и мощность используемого алфавита.

Необходимо определить какое количество информации содержит слово «Привет».

Однако мы не сможем воспользоваться этой формулой, поскольку нам не известно какое количество информации несет один знак ($I$).

Единицы измерения информации

Проведем несложный расчет и получим, что страница содержит:

$50 \cdot 60 = 3000$ байт информации.

Объем же информации, содержащейся в книге:

$3000 \cdot 50 = 150 \ 000$ байт.

Любая система единиц измерения содержит основные единицы и производные от них.

При измерении больших объемов информации на практике широко используются следующие производные от байта единицы, которые приведены в таблице:

Источник

Алфавитный подход к оценке количества информации. Формула Хартли

Оценка объема информации с точки зрения содержания оценивает количество данных с позиции минимизации неопределенных знаний.

Любой автоматизированный аппарат не имеет возможности улавливать самую суть содержимого данных, ведь автоматическая работа подразумевает лишь регистрировать электроимпульсные, либо их отсутствие. Из за подобной ситуации, ВЭМ требуются специфичный метод оценивания объема данных, который называют «алфавитный подход к определению количества информации».

Количественная оценка объема информации на основе алфавитного подхода

Метод алфавита подразумевает, что все варианты данных можно обозначить как специальный код из своеобразного количества символов, входящих в алфавит (при этом сам алфавит может быть любым). Средства хранения данных содержат разнообразные конечные последовательности, обладающие всеми признаками информации: хранение, передача, обработка человеком и электронно-вычислительными инструментами (например, компьютеры). Данный метод впервые описан Колмогоровым, где он отметил, что информация, содержащаяся в последовательности символов не связана с информацией непосредственного сообщения, а зависит лишь от самого маленького набора символов, которого хватает для составления кода. Такой способ обеспечивает ситуацию, при которой объем информации оценивается максимально объективно и не находится в зависимости от адресата, ожидающего данные. Информационная составляющая несет смысловую нагрузку только в момент выбора алфавита. Иногда ней можно пренебречь полностью.

Базой для развития данного метода является оценка количества символов в данных. Исходя из этого, можно понять, что смысл имеет лишь общая длина данных, без учета информативной ценности.

Следует учитывать, что длина данных может варьироваться в зависимости от такого фактора как «мощность алфавита». Данные особенности можно понять разобрав любую текстовую информацию. Язык не имеет значения, но проще будет оперировать текстом на родном языке.

Емкость информации, алфавитная мощность. Формула количества информации (формула Хартли)

Алфавитом принято называть совокупность символов, составляющих какой-либо язык. Под этими символами подразумеваются буквенные обозначения, реже знаки, цифровые обозначения, символы пробела и так далее.

Что же такое мощность алфавита? Мощность алфавита это обобщенное совокупность всех символов, в их полном количественном представлении.

Приведем пример, как определить мощность алфавита:

При использовании метода алфавита принято считать, что каждый отдельно взятый символ данных уже подразумевает некоторую емкость данных, находящуюся в зависимости от алфавитной мощности.

Последовательность символов для обозначения текстового сообщения содержит знаков – N. При самом простейшем варианте, когда длина кодировки соответствует всего лишь одному символу, источник посылает один из N вариантов текста, с таким количеством данных, которое будет соответствовать I.

Данное равенство названо в честь ученого Хартли, создавшего базу для развития теоретических основ учения об информации. В частности его работы отвечают на такие вопросы, как – «как найти мощность алфавита?» и «как обозначается информационный объём в информатике?».

По мнению Хартли: объем данных в тексте может быть подвержен неожиданных воздействиям извне, что взаимосвязано со степенью вероятного получения данных. Если эта степень минимальна, то данные будут малоинформативны и бесполезны для дальнейшей обработки.

Обратите внимание: в формуле Хартли абсолютно пренебрегается наличие неожиданных вводных. Формула Хартли (информатика) действует лишь при одинаковой степени вероятности расстановки знаков, при самодостаточной статистике.

К примеру, укажите, как записывается формула Хартли для расчета объема данных в символе двоичного кода:

Таким образом, информационная емкость такого символа будет равняться 1 биту.

Задачи: алфавитный подход к измерению информации (Пример 1)

Предположим, что информация создается поэтапно, с последовательностью в один знак (наподобие создания телеграммы). Пусть каждый отдельно взятый знак предположительно может являться любым алфавитным символом или обозначением. На практике, это не совсем соответствует действительности, но такой подход позволяет упростить решение.

Каждый этап появления знака соответствует теоретически любому символу N. С учетом, ранее изученной формулы Хартли, в каждом символе зашифрован определенный объем информации. Как же найти мощность алфавита в информатике? По искомой формуле символ хранит 1 бит данных:

Объем данных одной отдельно взятой буквы родного алфавита равен 5 битам.

То есть, формула отражает взаимосвязь всех возможных вариантов событийности и объем данных в определяемом тексте. В данной задаче: N – символы изучаемого алфавита, I – объем данных на один символ.

Текст содержит последовательность знаков с определённым объемом данных. Что такое мощность алфавита и как определить объем данных в тексте? По формуле: Ic=K*I, где Ic – объем данных текста, I- объем данных на один символ, К – расчет символов в тексте.

Практические примеры применения формулы в решении задач

Требуется подсчитать объем данных во фразе «Привет», с учетом 32х-буквенного алфавита (пренебрегаем символом «ё»».

Подсчитаем число знаков во фразе и алфавитную мощность (что такое мощность алфавита в информатике – смотрите выше).

Число знаков во фразе – 6 (К), алфавитная мощность соответствует 32 (N).

Подсчитываем объем данных на заданную фразу.

Перемножаем объем данных на один символ (I) и общее число символов на фразу, по ранее изученной формуле: Ic=K*I.

В данном моменте возникает трудность: нам не хватает данных об объеме информации на расчет одного знака.

Применим формулу Хартли. Так как текст набран с помощью алфавита с алфавитной мощностью соответствующей 32, мы можем уточнить, что объем данных соответствует 5 битам.

Рассчитав объем данных на один символ используемого алфавита и общий подсчет символов в изучаемой фразе, уточним объем данных фразы: Ic=K*I=6*5=30 бит.

При подобных расчетах чаще всего применяют алфавитный размер, который соответствует полной степени двух. Приведём пример: если N – 16, каждый знак содержит 4 бита данных (24 соответствует 16).

Информационные единицы

Максимум алфавитного размера не имеет никаких ограничений. Но стоит иметь в виду, что существует понятие «достаточности» алфавита; подобный вариант используется для работы на электронно-вычислительных машинах. Алфавитная мощность подобной модели соответствует 256 символам, в том числе содержит латиницу, кириллицу, цифровые обозначения, символы действий в арифметике, препинания.

Учитывая ранее полученный данные, известно, что 256 равно 28, а значит 1 знак такого вида алфавита содержит 8 бит данных. В информатике, это равно 1 байту.

При работе с данным алфавитным видом (ASCII-код) – максимально просто высчитывать количество данных в сообщении. Например, в приведенном примере: 1 знак равен 1 байту данных, что позволяет легко рассчитать общее число знаков (объем информации в виде байтов)

Предположим, что текстовое произведение среднего объема, в распечатке насчитывает около 25 листов (50 страниц). Одна страница имеет 50 строчек, а одна строчка – 60 знаков.

Рассчитаем объем одной страницы:

50*60=3000 байт информации

Рассчитаем объем всех данных произведения:

Каждая схема измерения включает единицы и их производные.

При расчете крупных информационных объемов – используются килобиты, мегабиты, гигабиты, килобайты, мегабайты, гигабайты.

Источник

Формула Хартли

Введение

Не получается понять каким образом производят измерение количества информации с помощью формулы Хартли? Выход есть! Записывайтесь ко мне на репетиторский урок по информатике и ИКТ. На своих индивидуальных уроках я делаю упор на практическое прорешивание колоссального количества различных тематических задач. Вы не только поймете ключевой смысл формулы Хартли, но также решите порядка 10 задач, связанных с измерением количества информации.

Формула Хартли позволяет определить количество информации, которая содержится в информационном сообщении длины n.

Для дальнейшего исследования нам потребуется познакомиться с таким понятием как мощность алфавита.
Мощность алфавита – это количество символов/знаков, из которых состоит рассматриваемый алфавит.

Примеры, связанные с мощностью алфавита

Количество букв в русскоязычном алфавите равно 33, следовательно, мощность русского алфавита составляет 33.

Количество арабских цифр, используя которые мы получаем различные числа, равно 10: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Следовательно, мощность алфавита арабских цифр составляет 10.

Азбука Морзе оперирует закодированными информационными сообщениями, состоящими из точек и тире, следовательно, мощность азбуки Морзе составляет 2.

Аналитический (в виде формульной зависимости) вид формулы Хартли

N – возможное количество различных информационных сообщений, шт;
m – количество символов/знаков в рассматриваемом алфавите, шт;
n – количество букв/элементов в информационном сообщении, шт.

Рассмотрим задачи, решаемые с применением формулы Хартли

Условие задачи №1:
Световое табло состоит из светящихся элементов, каждый из которых может гореть одним из 4-х различных цветов. Сколько различных сигналов можно передать при помощи табло, состоящего из 4-х таких элементов, при условии, что все элементы должны гореть.

Решение:
В данном примере под алфавитом необходимо понимать совокупность различных цветов, которыми могут гореть элементы. В условии задачи было сказано, что допускается четыре различных цвета, следовательно, мощность алфавита различных цветов составляет 4, то есть m = 4.

Под информационным сообщением следует понимать набор светящихся элементов. В условии упражнения говорится о 4-х подобных элементах, следовательно, длина сообщения составляет 4, то есть n = 4.

И осталось лишь определить количество различных сигналов, используя формулу Хартли:

N = m n = 4 4 = (2 2 ) 4 = 2 8 = 128 [сигналов].

Ответ: 128

Условие задачи №2:
Некоторый алфавит содержит 3 различных символа. Сколько слов длиной в 5 символов можно получить из данного алфавита (символы в слове могут повторяться)?

Решение:
В данном примере конкретно не уточняется о каком типе алфавита идет речь. Можно сделать предположение, что это какой-то символьный/знаковый алфавит. В условии задачи было сказано, что рассматриваемый алфавит содержит ровно 3 различных символа, следовательно, мощность данного алфавита составляет 3, m = 3.

Под информационным сообщением следует понимать некое слово. В условии задачи говорится о словах длиной в 5 символов, следовательно, длина информационного сообщения составляет 5, то есть n = 5.

И осталось лишь определить количество различных слов, используя могущественную формулу Хартли:

N = m n = 3 5 = 243 [слова].

Ответ: 243

Остались вопросы

Если у вас остались какие-либо вопросы по теме «Формула Хартли», то лаконично формулируйте и высылайте их мне на электронный адрес или записывайтесь ко мне на эффективный частный урок по информатике.

Источник

Содержание урока

Формула Хартли

Формула Хартли

Ответить на этот вопрос стало возможно только после того, как вы изучили логарифмы в курсе математики. Из формулы

сразу следует, что I — это степень, в которую нужно возвести 2, чтобы получить N, т. е. логарифм:

Эта формула называется формулой Хартли в честь американского инженера Ральфа Хартли, который предложил её в 1928 г.

Пусть, например, на лётном поле стоят 10 самолётов (с номерами от 1 до 10) и известно, что один из них летит в Санкт-Петербург.

Сколько информации в сообщении «Самолёт № 2 летит в Санкт-Петербург»? У нас есть 10 вариантов, из которых выбирается один, поэтому по формуле Хартли количество информации равно

I = log₂ 10 ≈ 3,322 бита.

Обратите внимание, что для значений N, которые не равны целой степени числа 2, количество информации в битах — дробное число.

С помощью формулы Хартли можно вычислить теоретическое количество информации в сообщении. Предположим, что алфавит (полный набор допустимых символов) включает 50 символов (в этом случае говорят, что мощность алфавита равна 50). Тогда информация при получении каждого символа составляет

I = log₂ 50 ≈ 5,644 бита.

Если сообщение содержит 100 символов, его общий информационный объём примерно равен

5,644 • 100 = 564,4 бита.

В общем случае объём сообщения длиной L символов, использующего алфавит из N символов, равен I = L • log₂ N.

Такой подход к определению количества информации называют алфавитным. Конечно, на практике невозможно использовать для кодирования символа нецелое число битов, поэтому используют первое целое число, которое больше теоретически рассчитанного значения. Например, при использовании алфавита из 50 символов каждый символ будет закодирован с помощью 6 битов (50 ≤ 2 6 = 64).

Сколько разных сообщений можно передать, если известен алфавит и длина сообщения? Предположим, что для кодирования сообщения используются 4 буквы, например «А», «Б», «В» и «Г», и сообщение состоит из двух символов. Поскольку каждый символ может быть выбран 4 разными способами, на каждый вариант выбора первого символа есть 4 варианта выбора второго. Поэтому общее число разных двухбуквенных сообщений вычисляется как 4 • 4 = 4 2 = 16. Если в сообщение добавить ещё один символ, то для каждой из 16 комбинаций первых двух символов третий можно выбрать четырьмя способами, так что число разных трёхсимвольных сообщений равно 4 • 4 • 4 = 4 3 = 64.

Следующая страница Задачи

Cкачать материалы урока

Источник