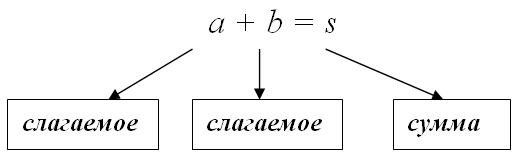
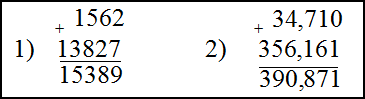Что означает найди сумму чисел
Что такое вычислить сумму чисел
Сумма чисел – это простое (базовое) математическое решение, выражающееся в увеличении исходного числа на заданное.
Визуально операцию суммирования можно представить следующим образом – положите на стол одно яблоко, а затем положите ещё два яблока. Итого получится три яблока. Это и есть сумма чисел яблок.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлено определение суммы чисел и самый простой онлайн калькулятор расчета расчета суммы чисел.
Вычислить сумму чисел до данного
Сделайте три варианта решения:
Пример работы вашей функции:
P.S. Какой вариант решения самый быстрый? Самый медленный? Почему?
Решение с помощью цикла:
Решение через рекурсию:
Решение по формуле: sumTo(n) = n*(n+1)/2 :
P.S. Надо ли говорить, что решение по формуле работает быстрее всех? Это очевидно. Оно использует всего три операции для любого n, а цикл и рекурсия требуют как минимум n операций сложения.
Вариант с циклом – второй по скорости. Он быстрее рекурсии, так как операций сложения столько же, но нет дополнительных вычислительных затрат на организацию вложенных вызовов. Поэтому рекурсия в данном случае работает медленнее всех.
Определение суммы чисел
Задание. Найти сумму чисел:
Ответ.
Свойства суммы чисел
На основании этих свойств можем заключить, что от перестановки мест слагаемых сумма не изменяется.
Дистрибутивность по отношению к умножению
$$(n+m) cdot k=n cdot k+m cdot k$$
Задание. Найти сумму чисел удобным способом:
Решение. По свойствам сложения имеем
При сложении больших чисел или десятичных дробей используется сложение в столбик.
Задание. Найти сумму чисел удобным способом:
Решение. Складываем эти числа в столбик, для этого запишем их друг под другом, разряд под разрядом. В случае десятичных дробей ориентируемся на то, чтобы запятая первого числа стояла под запятой второго. Далее складываем числа стоящие друг под другом, двигаясь справа на лево и записывая результата под чертой дроби. Если сумма чисел в одном столбце превышает десять, то количество десятков прибавляем к числам стоящим в следующем столбце слева от этого столбца:
Сложение рациональных дробей производится по правилу
Задание. Найти сумму чисел:
Решение. Вычислим первую сумму используя правило сложения рациональных чисел
Числитель и знаменатель полученной дроби можно сократить на 2, тогда в ответе получим
Для вычисления второй суммы, преобразуем сначала второе слагаемое в неправильную дробь, для этого умножим целую часть на знаменатель и прибавим полученное число к числителю. Далее применим правило сложение рациональных дробей
Выделим в полученной дроби целую часть, для этого разделим числитель на знаменатель с остатком. Полученное частное запишем в целую часть, а остаток от деления в числитель.
Что такое сумма чисел
Определение суммы чисел
Задание. Найти сумму чисел:
Ответ.
Свойства суммы чисел
На основании этих свойств можем заключить, что от перестановки мест слагаемых сумма не изменяется.
Дистрибутивность по отношению к умножению
$$(n+m) \cdot k=n \cdot k+m \cdot k$$
Что такое сумма чисел не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Найти сумму чисел удобным способом:
Решение. По свойствам сложения имеем
При сложении больших чисел или десятичных дробей используется сложение в столбик.
Задание. Найти сумму чисел удобным способом:
Решение. Складываем эти числа в столбик, для этого запишем их друг под другом, разряд под разрядом. В случае десятичных дробей ориентируемся на то, чтобы запятая первого числа стояла под запятой второго. Далее складываем числа стоящие друг под другом, двигаясь справа на лево и записывая результата под чертой дроби. Если сумма чисел в одном столбце превышает десять, то количество десятков прибавляем к числам стоящим в следующем столбце слева от этого столбца:
Сложение рациональных дробей производится по правилу
Задание. Найти сумму чисел:
Решение. Вычислим первую сумму используя правило сложения рациональных чисел
Числитель и знаменатель полученной дроби можно сократить на 2, тогда в ответе получим
Для вычисления второй суммы, преобразуем сначала второе слагаемое в неправильную дробь, для этого умножим целую часть на знаменатель и прибавим полученное число к числителю. Далее применим правило сложение рациональных дробей
Выделим в полученной дроби целую часть, для этого разделим числитель на знаменатель с остатком. Полученное частное запишем в целую часть, а остаток от деления в числитель.
Сумма и разность чисел
Что такое сумма, и как ее найти
Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.
Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.
Как найти разность чисел

А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.