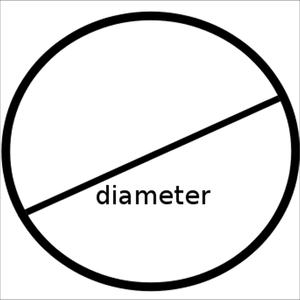
Что означает ноль с палочкой внутри

Символ, обозначение и значок диаметра: три способа его вставки

Все способы будут подробно рассмотрены и представлены в этой статье.

В каких ситуациях появляется потребность символа диаметра?

Существует масса ситуаций, при которых появляется такая потребность вставить знак «Ø» в нужный электронный файл. Для примера, он может потребоваться при составлении чертежей, детальном оформлении прайс-листов, оформлении рекламных продуктов или обозначения трубных изделий или запорной арматуры. Ученики, студенты или работники всяческих учреждений, предприятий либо организаций повседневно используют данный знак в процессе своей учебной, либо трудовой деятельности.

Перечислять примеры применения значка диаметра можно бесконечно долго, но и так понятно, что в некоторых ситуациях без него приходится достаточно трудно либо не комфортно. Именно поэтому далее по тексту мы рассмотрим три способа вставки символа диаметра в электронный документ.

Первый способ

Самым популярным способом можно назвать использование кодов ASCII. Он может быть осуществлен непосредственно самой ОС Windows. Для его реализации важно знать код – «0216», который в таблице кодов ASCII распознается как знак «Ø». Алгоритм ввода будет таковым:

Главное достоинство данного способа это то, что он универсален. Он может работать во многих существующих приложениях. Особенность способа состоит в том что сам символ, в качестве исходника не нужен. Недостаток данного метода в том, что всегда нужно знать код.

Второй способ

Программа Word и другие приложения взаимозаменяемый метод ввода «Ø» связан с определенным набором таких программных приложений, как: Microsoft Office Word, Excel и других. Для примера введем знак диаметра в » Word». В других случаях алгоритм ввода будет аналогичным. Во время работы заходим на панель инструментов на вкладку «Вставка». Она расположена в верхней части экрана между закладками «Главная» и «Разметка страницы». Наводим на эту вкладку курсор мыши и кликаем один раз левой кнопкой. После этого в правой части экрана видим панель «Символы». Там выбираем строку «Символ» и в появившемся списке нажимаем «Другие символы». Все эти действия осуществляются правой кнопкой мышки.

Теперь можно наблюдать открывшееся окно вставки. Находим нужный нам знак «Ø» за счет прокрутки найденных символов. В этом нам поможет колесо мыши. После удачного поиска «Ø», выделяем его одним нажатием левой кнопки мыши и кликаем кнопку «Вставить». После этого закрываем окно. Затем наверняка появиться значок диаметра в Word (в рабочей зоне). Отрицательная сторона данного способа в том, что он будет работать только в одной группе программных продуктов. Поэтому везде его применить невозможно.

Третий способ

Так же одним из способов вставки «Ø» является применение буфера обмена и использование функций «Копировать» и «Вставить». Буфер обмена это определенная часть памяти компьютерной операционной системы, которая предназначена для временного хранения информации. Сначала требуется найти где-нибудь такой символ.

В качестве примера, можно значок диаметра вставить в ворд (word) в соответствии с вышеизложенным алгоритмом. После чего его выделяем и копируем (по желанию можно использовать так называемые горячие клавиши «Ctrl»+»C»). Затем заходим в иное приложение и осуществляем действие вставки («Ctrl»+»V»). Отрицательная сторона данного способа заключается в том, что в любом случае нужен исходный символ. А так бывает далеко не всегда.

Видео

Источник

Математика, которая мне нравится

Математика для школьников и студентов, обучение и образование

Число 0

Выкладываю интересные свойства числа , которые прислал Лейб Александрович Штейнгарц.

1. Число в обычных арифметических операциях ведет себя совершенно уникально:

2. Число — это единственное число, на которое нельзя делить.

3. Очень своеобразно ведет себя число при возведении в степень:

4. Факториал числа тоже совершенно необычен:

5. Число — это единственное действительное число, которое не является ни положительным, ни отрицательным.

6. В центре города Будапешт (Венгрия) находится памятник НУЛЮ.

Цифра означает начало всех дорог по Венгрии. От этого памятника отмеряются все расстояния в стране.
Нуль — это единственная цифра, которой поставлен памятник.

7. В теории множеств Георг Кантор обозначил минимальную мощность бесконечных множеств (то есть мощность счетных множеств) так:

8. До конца XIX века в различных странах для отсчёта географических долгот использовали свои собственные национальные НУЛЕВЫЕ меридианы. По мере развития геодезии отсутствие стандартной системы долгот было признано международным астрономическим сообществом неудобным.

В 1884 году на Международной меридианной конференции в Вашингтоне за начало отсчёта долгот (то есть за НУЛЕВОЙ меридиан) на всём земном шаре было предложено принять Гринвичский меридиан.

9. Число 0 имеет два названия: НУЛЬ и НОЛЬ.

Оба названия в свободном употреблении — равноправны. Но в некоторых устойчивых выражениях эти слова не взаимозаменяемы. Например, только нуль в выражениях:

Но только ноль в таких выражениях:

10. Абсолютный НУЛЬ температуры — минимальный предел температуры, которую может иметь физическое тело во Вселенной. Абсолютный нуль служит началом отсчёта абсолютной температурной шкалы. По шкале Цельсия абсолютному нулю соответствует температура −273,15° C.

11. Из всех векторов только НУЛЕВОЙ вектор нельзя изобразить в виде направленного отрезка.

12. На любом калькуляторе после его включения сразу появляется ЕДИНСТВЕННОЕ число — цифра .

13. Первая цифра натурального числа может быть любой, кроме цифры .

14. 4. В полночь на электронных часах появляются четыре НУЛЯ.
Начинается новый день!

15. КРЕСТИКИ-НОЛИКИ — логическая игра, в которой один из игроков играет “крестиками”, а второй — “ноликами”.

16. Только цифра пишется точно так же, как одна из букв — а именно, как буква О.

Раньше цифра писалась с черточкой внутри знака (иногда, как пишется греческая буква Тэта), чтобы отличать ее от буквы О.

Ноль без этой палочки был то ли цифрой, то ли буквой. Поэтому и стали иногда говорить “НОЛЬ БЕЗ ПАЛОЧКИ”,

17. Жест рукой, изображающий цифру , в англоговорящих странах имеет значение “ВСЕ В ПОРЯДКЕ”, “ВСЕ НОРМАЛЬНО”, “ВСЕ ОТЛИЧНО”.

18. Замкнутая орбита любого космического тела — это ЭЛЛИПС, который по форме полностью совпадает с формой цифры .

19. НУЛИ функции — это числа из области определения функции, при которых она принимает НУЛЕВОЕ значение.

20. Следующее свойство числа очень хорошо иллюстрируется известным стихотворением Самуила Яковлевича Маршака.

21. На клавиатуре компьютера цифры изображают в таком порядке

Эта числовая последовательность является ПОЧТИ возрастающей. Нарушает порядок только лишь цифра .

22. В 1964 году была впервые напечатана замечательная книга “ПРИКЛЮЧЕНИЯ НУЛИКА”. Эта “сказка да не сказка”, которую придумали Эмилия Александрова и Владимир Лёвшин о числах, их загадках и странностях.

А затем по этой книге был создан музыкальный спектакль, и даже была выпущена пластинка.

23. Это стихотворение о НУЛЯХ сочинил доктор физико-математических наук Герцен Исаевич Копылов (1925–1976), чья замечательная задача о правильном многоугольнике также имеется в САЛОНЕ КРАСОТЫ
(см. п. 10 здесь)

Комментариев: 20

1 Алексей:

Полагаю, что в пункте 16 толкование выражения – “нуль без палочки”, ошибочно. Вспомним А.С. Пушкина: “Мы почитаем всех нулями, а единицами – себя!” Под палочкой подразумевается “единица” с соответствующим изменением предложенного толкования в п.16.

Лейб Reply:
Февраль 24th, 2013 at 14:31

Конечно, можно придерживаться и такой версии.

2 Вячеслав:

К пункту 4, непонятно, как факториал числа 0 может быть равен 1.

Иван Reply:
Январь 10th, 2016 at 19:28

По определению факториала

3 Лейб:

Так математики приняли – по определению.
По разным причинам, математики посчитали, что так УДОБНО.
Доказать это нельзя.
Так же, как, например, принято, что
.

.
.
Это тоже принято ПО ОПРЕДЕЛЕНИЮ.

Елена Reply:
Июнь 2nd, 2013 at 1:00

Вовсе нет.
(а^n):(а^n)=1,
C другой стороны
(а^n):(а^n)=а^(n-n)=a^0
отсюда
a^0=1

Лейб Reply:
Июнь 5th, 2013 at 10:19

К сожалению, эти рассуждения нельзя принять за доказательство.
.
Дело в том, что в четвертой строчке вычитаются одинаковые показатели степени.
Но ведь это должно иметь обоснование.

Но его нельзя сделать, если до этого еще не была ОПРЕДЕЛЕНА степень с нулевым показателем.

Елена Reply:
Июнь 2nd, 2013 at 1:10

Про 0!
1! = 1
2! = 1!*2
2! = 2
3! = 2!*3
3! = 6
4! = 3!*4
4! = 24
и так далее
а теперь обратно
4! = 24
3! = 4!/4
3! = 6
2! = 3!/3
2! = 2
1! = 2!/2
1! = 1
0! = 1!/1
0! = 1

Или исходя из комбинаторной задачи, откуда факториал собственно и взялся
3 разных предмета можно разместить 3!=6 способами.
2 разных предмета 2!=2 способоами
1 предмет – одним способом (просто есть предмет) 1!=1
0 предметов – опять-таки одним способом (просто нет предметов) 0! = 1

Лейб Reply:
Июнь 5th, 2013 at 10:25

4 Technik:

5 Геннадий:

Никакое число не может быть одновременно ни положительным и ни отрицательным. Иначе это будет не число. Ноль – это, все-таки, число, и принято считать его положительным. Может быть, потому что перед ним лишь в особых случаях ставят знак “минус”.

Факториал 0! сам по себе не имеет смысла, исходя из непосредственного определения факториала (недавно писал об этом). Математики договорились считать 0!=1, поскольку это помогает упростить и сделать более удобными и красивыми многие формулы, например, в дискретном анализе.

Двойка в степени 0 равна 1, и это доказывается в теории пределов: значение при стремлении к бесконечности приближается именно к 1.

Heart-shaped glasses Reply:
Июнь 15th, 2014 at 0:13

Геннадий, а можно ссылку на источник, в котором утверждается, что ноль — положительное число?

Геннадий Reply:
Июнь 18th, 2014 at 10:26

Heart-shaped glasses, а я и не утверждал, что ноль является положительным числом, лишь написал, что это принято считать. Например, повторюсь, принято считать 0!=1, но утверждать нельзя, поскольку сама запись 0! бессмысленна.
Наверное, надо было сказать более аккуратно, более осторожно, например: ноль тяготеет к положительным числам. Давайте посмотрим на натуральные числа. Отрицательные числа натуральными не являются, и это признают все безоговорочно. Значит, все натуральные числа положительны. Но многие и не то, чтобы отдельные математики, а целые математические школы, относят ноль к натуральным числам. Вот и делайте выводы сами.
И последнее, Бурбаки рассматривают натуральные числа как мощности конечных множеств. Отрицательное число никак нельзя привязать к мощности какого-либо множества. А число ноль прекрасно вписалось в такую конструкцию, поскольку ноль – это мощность пустого множества, и в теории множеств без пустого множества не обойтись.

Намсек Reply:
Май 26th, 2015 at 18:59

Sorry for writing in English but I’m learning Russian and I don’t know grammar well enough yet.

When I was 4 years old and I had just been told at school that there were odd and even numbers, I asked my father whether zero was odd or even. He replied “what the hell of a question is that?”
Twenty years later I thought about it again and I concluded that it was neither, since it doesn’t exist. There I also understood that it IS NOT actually a number.
Numbers are quantifications of something, zero is nothing. It means there is nothing to quantify.

Zero is used in mathematics to mean an empty space. It means “nothing”. And nothing is no way on earth, positive, negative, odd or even.
To be clear, there is nothing that could be negative or positive there. Nothing is there and nothing is missing.
Positive numbers are energy/matter becoming stars, negative numbers are energy/matter becoming black holes. Zero is the void. The void cannot become a star or a black hole.

The question does not subsist.

Btw, zero “is” odd. It can’t be divided by two.

Геннадий Reply:
Май 28th, 2015 at 11:32

Hello, Hamcek! Извините, дальше на русском. Я тоже только учу английский и боюсь напутать с грамматикой.
Ниже отвечаю и Вам и всем, кто на этой ветке необоснованно принижает ноль. Особенно меня удивила Ваша уничижительная отповедь уважаемому, достойному из достойных и, на мой взгляд, крайне необходимому числу 0.

Ss.Lemon Reply:
Сентябрь 30th, 2016 at 0:13

…what goes on in “empty space” determines the properties of the three-dimensional existence we know and love…nothingness is everything
(“The Mystery of Empty Space”
University of California Television (UCTV))

6 Георгий:

Вы не ошибаетесь на счёт Будапешта?
Это ж нулевой километр! Начало всех дорог Венгрии.
Там и написано внизу КМ.
В Москве тоже есть нулевой КМ рядом с Красной площадью, но к памятнику НУЛЮ имеет нулевое отношение.

7 Геннадий:

Попробую защитить число 0.
Отношение уважаемого автора и многих комментаторов к нулю (особенно удивил и расстроил Hamcek) навеяло известную картину: древние времена, луг, пасутся овцы, ночь, пастух считает звезды – 1, 2, 3 и т.д. У пастуха звезды ассоциируются и, наверное, отождествляются с числами. Есть звезды – есть числа. А если облачность, и звезд нет? Сколько в этом случае звезд – ноль? Что же это за число ноль? Раз звезд нет, то и числа такого нет. Не число, а пустое место, вакуум. Именно так пишет Hamcek – the void.

Но сейчас мы знаем, что число ноль есть. Для него придумали цифру 0, и без этой цифры не обойтись. Не нравится порядок цифр на клавиатуре компьютера 1, 2, 3, 4, 5, 6, 7, 8, 9, 0? Не возрастают цифры? Ноль в конце списка портит всю картину, и значит ноль какой-то странный? Нет, с нулем все в порядке, просто на клавиатуре некорректно размещены цифры. Место нуля в начале ряда, если мы хотим выстроить цифры по ранжиру. В этом случае ноль по праву займет лидирующее место, ноль возглавляет колонну цифр, именно с нуля начинается отсчет времени в полночь. Уверен, ноль возглавит и натуральный ряд чисел. Не все с этим согласны, но это вопрос времени.

Если мы складываем или вычитаем два числа, то результат также число, и это число может оказаться нулем. Ноль – четное число и делится на 2 без остатка (http://ru.math.wikia.com/wiki/Чётные_и_нечётные_числа).

А делить на ноль можно, почему нет? Получим бесконечность, трансфинитное число (http://ega-math.narod.ru/Singh/Cantor.htm). Но надо уточнить в соответствии с условиями задачи или примера, с какой бесконечностью мы имеем дело. Минимальное трансфинитное число – это мощность счетного множества. Здесь приходится мириться, например, с тем, что количество всех натуральных чисел и количество четных чисел одинаково. Следующее трансфинитное число – мощность континуума. И здесь нам докажут, что точек на всей числовой оси столько же, сколько и на интервале (0,1).

Трансфинитных чисел бесконечное (видимо, счетное) множество. И если мы просто делим некоторое число на ноль, то возникает неопределенность лишь в том смысле, что надо определиться с трансфинитным числом.

Евгений Reply:
Сентябрь 28th, 2015 at 22:35

8 Александр Бережной:

Ещё Ноль – единственное число, в отношении которого мнения математиков расходятся. Считать ли ноль натуральным числом или не считать. В школе ноль натуральным числом не считают, а зря… ))

Источник

Ø (латиница)

Ø (латиница)

Это — статья о букве расширенной латиницы Ø. Не следует путать её с ∅ (знаком пустого множества) и с ⌀ (символом диаметра)

Буква латиницы Ø
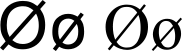Латинский алфавит
A	B	C	D	E	F	G
H	I	J	K	L	M	N
O	P	Q	R	S	T	U
V	W	X	Y	Z
Дополнительные и вариантные знаки
À	Á	Â	Ã	Ä	Å	Æ
Ā	Ă	Ą	Ç	Ć	Ĉ	Ċ
Č	Ð,ð	Ď,ď	Đ,đ	È	É	Ê
Ë	Ē	Ė	Ę	Ě	Ə	Ĝ
Ğ	Ġ	Ģ	Ĥ	Ħ	Ì	Í
Î	Ï	Ī	Į	İ,i	I,ı	IJ
Ĵ	Ķ	Ļ	Ł	Ñ	Ń	Ņ
Ň	Ò	Ó	Ô	Õ	Ö	Ø
Ő	Œ	Ơ	Ŕ	Ř	ß	ſ
Ś	Ŝ	Ş	Š	Þ	Ţ	Ť
Ù	Ú	Û	Ü	Ū	Ŭ	Ů
Ű	Ų	Ư	Ŵ	Ý	Ŷ	Ÿ
Ź	Ż	Ž

Ø и ø (латинская O диагонально перечёркнутая) — заглавная и строчная буквы, соответственно, используемые в датском, норвежском и фарерском алфавитах. Модификация латинской буквы O.

Коды

ASCII	Юникод	HTML-мнемоника
Ø (заглавная)	D8h	00D8h	Ø
ø (строчная)	F8h	00F8h	ø

См. также

Полезное

Смотреть что такое «Ø (латиница)» в других словарях:

Đ (латиница) — Буква латиницы Đ, đ (дьже) Латинский алфавит A B C … Википедия

Ð (латиница) — Буква латиницы Ð, ð (eth) Латинский алфавит A B C … Википедия

латиница — алфавит, письмо, латинский алфавит Словарь русских синонимов. латиница см. латинский алфавит Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Алексан … Словарь синонимов

Латиница — наряду с кириллицей (см.) и глаголицей (см.) одна из славянских азбук, представляющая применение букв латинского алфавита для начертания славянских звуков. Первые попытки такого применения известны еще до кириллицы и глаголицы, но эти попытки… … Литературная энциклопедия

ЛАТИНИЦА — см. Латинское письмо … Большой Энциклопедический словарь

ЛАТИНИЦА — ЛАТИНИЦА, латиницы, муж. (филол.). Латинский алфавит, латинское письмо. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

ЛАТИНИЦА — ЛАТИНИЦА, ы, жен. Латинский алфавит. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

Ł (латиница) — Польская буква Ł Латинский алфавит A … Википедия

Æ (латиница) — Лигатура Æ Латинский алфавит A … Википедия

IJ (латиница) — Нидерландская буква IJ Латинский алфавит A … Википедия

Œ (латиница) — Латинский алфавит A B C D E F G H I J K … Википедия

Источник