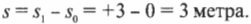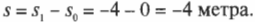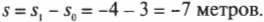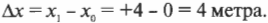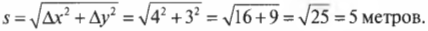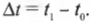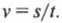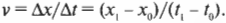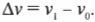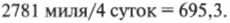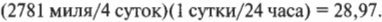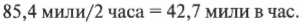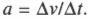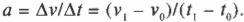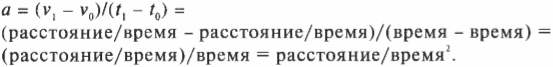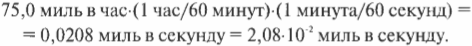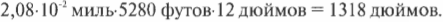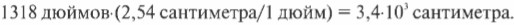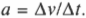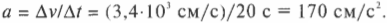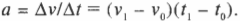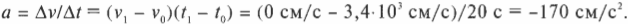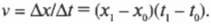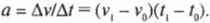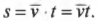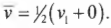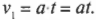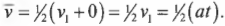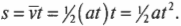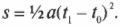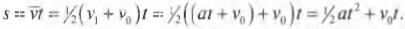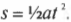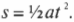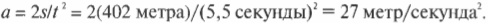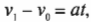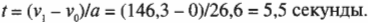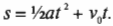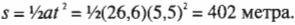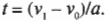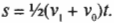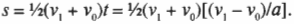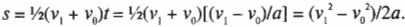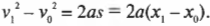Что означает отрицательное ускорение
Это ускорение можно рассматривать как отрицательное, в отличие от скорости, которая указывается как положительная. Хотя отрицательное ускорение не всегда вызывает снижение скорости.
Собака весело тормозит на песке. Ускорение при торможении можно рассматривать как отрицательное ускорение. Источник: Pixabay.
Перед тем как погрузить лапы в песок, собака двигалась с определенной скоростью v вперед, то есть положительной. Затем песок замедляется до полной остановки, то есть до нулевой конечной скорости.
Предположим, что все это произошло за промежуток времени Δt. Ускорение за это время будет рассчитываться следующим образом:
В приведенном выше уравнении v> 0, Δt> 0, тогда a
Следовательно, мы можем установить, что:
Формулы для расчета ускорения
Независимо от знака, среднее ускорение a m между моментами t и t ‘рассчитывается по следующей формуле:
Среднее ускорение предоставляет общую информацию о том, как изменилась скорость за рассматриваемый интервал времени. Со своей стороны, мгновенное ускорение дает подробную информацию о том, как скорость изменяется в каждый момент. Итак, для данного момента t ускорение рассчитывается по следующей формуле:
-Пример 1
В начальный момент t = 0,2 с объект имеет скорость 3 м / с. Позже, в момент t ‘= 0,4 с, он имеет скорость 1 м / с. Вычислите среднее ускорение между моментами времени t и t ‘и интерпретируйте результат.
Ответить
-Пример 2
Ответить
В заключение, в конце временного интервала скорость стала еще более отрицательной (-3 м / с).
Скорость, которая является модулем скорости, увеличилась, несмотря на отрицательное ускорение. Я имею ввиду, этот объект ускорился. Отсюда делаем вывод:
-Пример 3-Вертикальное подбрасывание.
Рассмотрим следующий пример: объект имеет мгновенную скорость, заданную следующим выражением, со всеми единицами измерения Международной системы:
Найдите скорость и ускорение для времен 0 с, 0,5 с и 1,0 с. В каждом случае укажите, ускоряется или замедляется объект.
Ответить
Скорость в каждый из указанных моментов времени находится путем прямой подстановки t в уравнение. Ускорение находится путем получения данного выражения как функции времени и последующей оценки результата в каждый из заданных моментов времени.
Ускорение постоянное и отрицательное для любого движения. Теперь можно описать, что случилось с мобильным телефоном в процессе его движения.
В момент t = 0 с мобиль замедлял ход. Это следует немедленно, поскольку скорость положительна, а ускорение отрицательна.
Выпускники наклоняются вертикально к шапкам. Источник: Pexels.
Когда мобильный телефон проецируется вертикально вверх, ему удается достичь максимальной высоты. Если в этом смысле выбрано положительное направление, что происходит почти всегда, в течение времени, необходимого для достижения этой максимальной точки, мобильный телефон будет иметь положительную скорость.
Но гравитация существовала все время. И он всегда направлен вертикально вниз, независимо от того, идет ли объект вверх или вниз. Естественно, ей удается постепенно замедлять работу мобильного телефона, пока он не остановится на мгновение.
Мобайл немедленно меняет скорость и возвращается к земле. В этом случае скорость отрицательна, потому что она также указывает на землю. Следовательно, гравитация заставляет скорость увеличиваться все больше и больше.
Наконец, при t = 1,0 с скорость мобильного телефона отрицательна. Если это вертикальный старт вверх, при отсутствии трения это означает, что он снова проходит через начальную точку, но на этот раз он идет вниз, а не вверх.
В заключение, отрицательное ускорение не обязательно означает, что мобильный телефон тормозит. Напротив, мобильный телефон может работать все быстрее и быстрее. Нужно обратить внимание на то, совпадают ли признаки скорости и ускорения.
Ускорение
Ускорение обозначается символом a:
Ускорение, как и скорость, является векторной величиной.
Преобразуем формулу ускорения дальше:
a = ΔV/Δt = (ΔS/Δt)/Δt = ΔS/Δt 2
1. Положительное и отрицательное ускорение
Ускорение, как и скорость, обладает знаком.
Если автомобиль разгоняется, его скорость возрастает, а ускорение имеет положительный знак.
Естественно, при равномерном движении ускорение равно нулю.
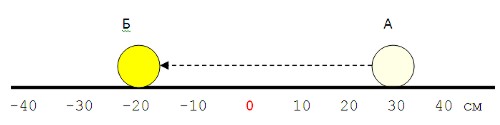
Пусть шар движется с замедлением, но имеет отрицательное перемещение!
Запомните!
2. Среднее и мгновенное ускорение
По аналогии со скоростью ускорение может быть средним и мгновенным.
Среднее ускорение вычисляется как разность конечной и начальной скоростей, которая делится на разность конечного и начального времени:
Среднее ускорение отличается от фактического (мгновенного) ускорения в данный момент времени. Например, при резком нажатии педали тормоза автомобиль получает большое ускорение в первый момент времени. Если же водитель затем отпустит педаль тормоза, то ускорение уменьшится.
3. Равномерное и неравномерное ускорение
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Как называется отрицательное ускорение?
Примечание: отрицательное ускорение также называется запаздывание и тело, как говорят, тормозит. Если бы объект A двигался в отрицательном направлении и ускорялся, тогда ускорение тела было бы в том же направлении, что и его скорость.
все же, что такое время разгона?
Ускорение скорость изменения скорости со временем. … Ускорение происходит каждый раз, когда скорость объекта увеличивается или уменьшается, или он меняет направление. Как и скорость, есть два вида ускорения: среднее и мгновенное. Среднее ускорение определяется за «большой» промежуток времени.
следующий: ускорение отрицательное или положительное?
Ускорение, 8 м / с ^ 2, представляет собой изменение скорости, и в данном случае оно находится в положительный направлении.
тогда как узнать, отрицательное ли ускорение?
Согласно нашему принципу, когда объект замедляется, ускорение происходит в направлении, противоположном скорости. Таким образом, этот объект имеет отрицательное ускорение.
Означает ли замедление отрицательное ускорение?
Под замедлением всегда понимается ускорение в направлении, противоположном направлению скорости. Замедление всегда снижает скорость. … Следовательно, отрицательное ускорение в нашей системе координат, потому что его ускорение направлено влево.
Что происходит при нулевом ускорении?
Если нет ускорения, то объект будет двигаться с постоянной скоростью. Математически мы можем взглянуть на второй закон Ньютона и формулу ускорения. … Поскольку мы знаем, что масса не может быть нулевой, ускорение должно быть нулевым.
Что такое положительное ускорение?
Когда объект ускоряется, ускорение происходит в том же направлении, что и скорость.. Таким образом, этот объект имеет положительное ускорение.
По какой формуле рассчитывается ускорение?
Почему ускорение отрицательное?
Ускорение отрицательное когда объект движется в положительном направлении, но скорость изменения скорости отрицательная (скорость уменьшается). Мы также можем определить эти два ускорения, когда объект движется в отрицательном или противоположном направлении (справа налево).
Какой пример нулевого ускорения?
Может ли быть ускорение при нулевой скорости?
Ответ: Да, объект может иметь нулевую скорость и одновременно ускоряться. Рассмотрим объект, движущийся в прямом направлении.
В чем разница между отрицательным ускорением и замедлением?
Как получить отрицательное ускорение?
Обратите внимание, что объект внизу движется в положительном направлении с изменяющейся скоростью. Объект, движущийся в положительном направлении, имеет положительную скорость. Если объект замедляется, то его вектор ускорения направлен в направлении, противоположном его движению. (в данном случае отрицательное ускорение).
Что такое отрицательное ускорение, приведите пример?
Но отрицательное ускорение означает, что скорость изменения скорости отрицательна или скорость уменьшается. Пример: (1) Когда мы тормозим движущуюся машину, то на него действует отрицательное ускорение и машина останавливается. (2) Когда мы бросаем мяч вверх, на него действует также отрицательное ускорение.
В чем разница между замедлением и уменьшением ускорения?
Под замедлением часто подразумевают замедление. Отрицательное ускорение может просто означать ускорение в отрицательном направлении. Уменьшение ускорения может означать изменение ускорения в отрицательном направлении или просто то, что величина ускорения уменьшается.
Означает ли 0 скорость 0 ускорение?
Для того, чтобы получить большая часть скорости не равна нулю, если объект ускоряется. … Однако, если скорость постоянна, ускорение равно нулю (поскольку скорость не меняется со временем). Хотя в определенный момент времени при ускорении можно иметь нулевую скорость.
Как узнать, что ускорение равно 0?
Когда ускорение равно нулю (то есть a = dv / dt = 0), скорость изменения скорости равна нулю. То есть ускорение равно нулю, когда скорость объекта постоянна. Графики движения отображают изменения расстояния, скорости и ускорения во времени.
НЕТ. Потому что нулевое ускорение означает отсутствие изменения ускорения. Это не увеличение или уменьшение ускорения на протяжении всего пути. С другой стороны, постоянное ускорение означает постоянное увеличение или уменьшение ускорения.
Ускорение, скорость, с которой скорость изменяется со временем, с точки зрения скорости и направления. Поскольку ускорение имеет как величину, так и направление, это векторная величина. … Скорость также является векторной величиной.
Что такое пример формулы ускорения?
Какие есть 3 способа ускорения?
Есть три способа ускорения объекта: изменение скорости, изменение направления или изменение скорости и направления.
Какова формула ускорения и скорости?
| Водоизмещение | Δx = xf − xi |
|---|---|
| Средняя скорость | –V = v0 + v2 |
| Скорость от ускорения | v = v0 + при (константа) |
| Положение от скорости и ускорения | x = x0 + v0t + 12at2 (константа) |
| Скорость на расстоянии | v2 = v20 + 2a (x − x0) (константа) |
У вас может быть отрицательное ускорение?
Он не ускоряется и не замедляется, поэтому он нулевое ускорение. Поскольку скорость / скорость этого объекта со временем уменьшается, это означает отрицательное ускорение.
Когда скорость автомобиля отрицательная, а ускорение отрицательное?
Объект, который движется в отрицательном направлении имеет отрицательную скорость. Если объект ускоряется, то его вектор ускорения направлен в том же направлении, что и его движение (в данном случае отрицательное ускорение).
Является ли замедление отрицательным ускорением?
Под замедлением всегда понимается ускорение в направлении, противоположном направлению скорости. Замедление всегда снижает скорость. … Следовательно, отрицательное ускорение в нашей системе координат, потому что его ускорение направлено влево.
Соответственно, что называется отрицательным ускорением?
Тело, имеющее отрицательное ускорение, называется замедляющийся. Следовательно, отрицательное ускорение тела можно назвать замедлением тела. … Поскольку ускорение является вектором, отрицательный знак в уравнении (1) указывает, что ускорение тела имеет направление, противоположное скорости тела.
следующий: может ли быть ускорение, если скорость равна нулю?
Ответ: Да, объект может иметь нулевую скорость и одновременно ускоряться. Рассмотрим объект, движущийся в прямом направлении.
Таким образом, в чем разница между замедлением и уменьшением ускорения? Под замедлением часто подразумевают замедление. Отрицательное ускорение может просто означать ускорение в отрицательном направлении. Уменьшение ускорения может означать изменение ускорения в отрицательном направлении или просто то, что величина ускорения уменьшается.
Что происходит при нулевом ускорении?
Если нет ускорения, то объект будет двигаться с постоянной скоростью. Математически мы можем взглянуть на второй закон Ньютона и формулу ускорения. Мы знаем, что сила равна нулю.
Ускорение отрицательное или положительное?
Ускорение, 8 м / с ^ 2, представляет собой изменение скорости, и в данном случае оно находится в положительный направлении.
Почему замедление называется отрицательным ускорением?
Если скорость объекта уменьшается, то объект считается, что ускорение отрицательное, и значение замедления уменьшается. Следовательно, замедление означает отрицательное ускорение.
Какой пример отрицательного ускорения?
→Когда вы плюхаетесь на кровать, вы испытываете отрицательное ускорение. Когда вы кладете объект на стол, он тоже испытывает отрицательное ускорение. … → Когда движущийся объект со временем постоянно теряет скорость, движение имеет отрицательное ускорение или замедление.
Почему ускорение максимальное при нулевой скорости?
Максимальная скорость тела означает, что ее нельзя увеличивать дальше. Средства изменение скорости равно нулю. Означает, что изменение скорости равно нулю. Следовательно, ускорение равно нулю.
В какой точке или позиции ускорение является максимальным?
В положении равновесия, скорость максимальна, а ускорение (а) упало до нуля.
Может ли тело иметь равномерное ускорение?
Поскольку скорость изменения скорости известна как ускорение, и для равномерного ускорения скорость изменения скорости также должна быть единой ставкой это единственное условие, при котором тело имеет равномерное ускорение.
Как скорость влияет на ускорение?
Что такое уменьшение ускорения?
Что такое среднее ускорение?
Среднее ускорение относится к скорости изменения скорости.. Мы делим изменение скорости на прошедшее время, чтобы узнать среднее ускорение чего-либо. Например, если скорость сумасшедшего мяча увеличивается с 0 до 60 см / с за 3 секунды, среднее ускорение мяча будет 20 см / с / с.
Как узнать, что ускорение равно 0?
Когда ускорение равно нулю (то есть a = dv / dt = 0), скорость изменения скорости равна нулю. То есть ускорение равно нулю, когда скорость объекта постоянна. Графики движения отображают изменения расстояния, скорости и ускорения во времени.
Что происходит с ускорением, если скорость не меняется?
Почему ускорение отрицательное?
Согласно нашему принципу, когда объект замедляется, ускорение происходит в направлении, противоположном скорости. Таким образом, этот объект имеет отрицательное ускорение. … Когда объект ускоряется, ускорение совпадает с направлением скорости. Таким образом, этот объект также имеет отрицательное ускорение.
Что будет после разгона?
| производная | терминология | смысл |
|---|---|---|
| 1 | скорость | скорость изменения позиции |
| 2 | ускорение | скорость изменения скорости |
| 3 | придурок | скорость изменения ускорения |
| 4 | вздрогнуть (щелкнуть) | скорость изменения рывка |
В чем разница между ускорением и замедлением?
Скорость изменения скорости объекта во времени определяется как ускорение. … Увеличение скорости объекта в единицу времени называется ускорением. Замедление обратное ускорение и определяется как уменьшение скорости в единицу времени.
Какая формула замедления?
Что такое замедление или отрицательное ускорение?
Какая сила вызывает отрицательное ускорение?
Если объект замедляется тогда его вектор ускорения направлен в направлении, противоположном его движению (в данном случае отрицательное ускорение).
Как рассчитать отрицательное ускорение?
Это можно найти с помощью уравнения а = Δv ÷ Δt. Когда скорость объекта уменьшается (замедляется), это называется замедлением. Это также может быть представлено отрицательным ускорением. Это означает, что направление или вектор ускорения указывает в направлении, противоположном движению объекта.
Когда скорость минимальна Что такое ускорение?
В части (b) показано мгновенное ускорение при минимальной скорости, которое также нуль, поскольку и здесь наклон кривой равен нулю. Таким образом, для данной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость.
Что такое ускорение на максимальной скорости?
В какое время скорость максимальна?
Теперь мы знаем, что скорость максимальна, когда у = 0, т.е. смещение равно нулю, а ускорение равно нулю, что означает, что система находится в равновесии. Следовательно, в точке простого гармонического движения максимальная скорость может быть вычислена по формуле v = Aω.
Глава 3. Утоляем жажду скорости
Представьте себе, что вы участвуете в гонке “ Формула-1” и в гоночном автомобиле мчитесь навстречу славе. Скорость огромна, ветер свистит, а уверенность в победе высока, ведь отрыв от соперников значителен и осталось пройти последний поворот. Похоже, что ближайший преследователь, чемпион прошлого года, также прилагает значительные усилия — в зеркале заднего вида на мгновение показалась серебристая обшивка его болида. Необходимо что-то предпринять, поскольку преследователь очень быстро сокращает отставание.
Вам известно все или почти все о скорости и ускорении. С такими знаниями вы знаете, что нужно делать: жмете на педаль газа, и болид ускоряется. Знание законов изменения скорости позволило с легкостью пройти последний поворот. А вот и взмах клетчатого флага на финише, к которому вы пришли за рекордное время. Отлично! Безусловно, вам помогло знание именно тех тем, которые излагаются в этой главе: перемещение, скорость и ускорение.
Наверняка у вас уже есть интуитивное представление об этих понятиях, иначе вы не смогли бы управлять автомобилем или даже велосипедом. Перемещение описывает изменение места расположения, скорость характеризует быстроту перемещения, а ускорение знакомо всякому, кому приходилось перемещаться в автомобиле. С этими понятиями люди сталкиваются ежедневно, а физика поможет организовать их изучение. Знание этих физических понятий позволяет планировать дороги и транспортные развязки, строить и запускать космические корабли, отслеживать движение планет, предсказывать погоду, а также… приводит нас в бешенство в дорожной пробке.
Понимание законов физики включает понимание основ движения, и именно этой теме посвящена данная глава. Приступаем.
Передвигаемся и перемещаемся
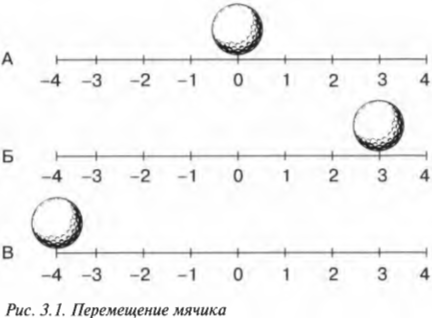
С точки зрения физики перемещение возникает при переходе какого-то объекта из точки 1 в точку 2. Попросту говоря, перемещение — это пройденное объектом расстояние. Рассмотрим, например, движущийся вдоль линейки мячик для игры в гольф, который показан на рис. 3.1. Допустим, что сначала мячик находится возле отметки 0 (схема А).
Пока что все в порядке. Допустим, что мячик сместился на новое место, например на 3 метра вправо (схема Б). В таком случае говорят, что мячик переместился, или произошло перемещение. В данном случае перемещение равно 3 метрам. В исходном положении мячик находился на отметке 0 метров, а в конечном положении — на отметке +3 метра.
В физике перемещение часто обозначают символом \( s \) , т.е. в данном случае \( s \) равно 3 метрам.
Как и любое другое измерение в физике, перемещение выражается в некоторых единицах, обычно в сантиметрах или метрах. Но часто можно встретить и другие единицы: километр, дюйм, фут, миля или даже световой год (расстояние, которое проходит свет за один год и которое тяжело измерить обычной линейкой; оно приблизительно равно 9 460 800 000 000 километрам или 9 460 800 000 000 000 метрам).
Ученые любят очень подробно описывать разные ситуации. Например, исходное положение часто обозначают символом \( s_0 \) (или, в англоязычной литературе, \( s_i \) где \( i \) обозначает “initial”, т.е. исходный). А конечное положение часто обозначают символом \( s_1 \) (или, в англоязычной литературе, \( s_f \) где \( f \) обозначает “final”, т.е. конечный). Таким образом, положения на схеме А и схеме Б на рис. 3.1 выражаются символами \( s_0 \) и \( s_1 \) соответственно. А перемещение \( s \) между ними равно их разности, т.е. конечное положение минус исходное положение:
Обратите внимание, что \( s \) отрицательно!
В качестве начальной точки можно выбрать отличное от 0 положение. Например, для перехода между исходным положением на схеме А на рис. 3.1 и конечным положением на схеме В получим следующее перемещение:
Величина перемещения зависит от выбора начальной точки. В простых задачах выбор начальной точки очевиден, а как быть в более сложных случаях, например, когда движение происходит не вдоль линейки?
Разбираемся с осями
В реальном мире объекты редко движутся вдоль линеек, как мячик для гольфа на рис. 3.1. Часто движение происходит в двух или даже трех измерениях пространства. Чтобы измерить движение в двух пространственных измерениях, нужно иметь две пересекающиеся линейки, которые называются осями. Горизонтальную ось называют осью X, а вертикальную — осью Y, а при движении в трехмерном пространстве используют еще одну ось Z (если представить, что оси X и Y лежат в плоскости страницы, то ось Z как бы “торчит” из нее).
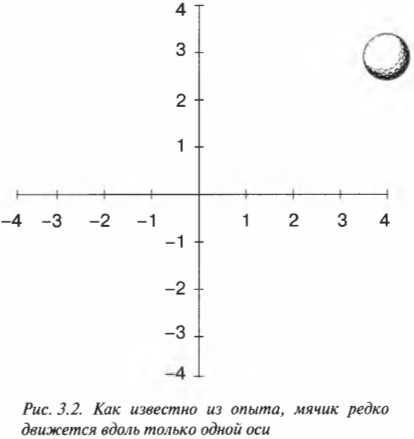
На рис. 3.2 показан пример движения мячика для гольфа в двумерном пространстве. Мячик движется из центра рисунка в верхний правый угол.
Чему равно перемещение? Изменение положения по оси X обозначается символом \( \Delta x \) (греческий символ \( \Delta \) произносится “дельта” и означает “изменение”) и равно: конечное положение минус исходное положение. Если мячик стартует из центра рисунка, т.е. из положения (0; 0), то изменение положения по оси X равно:
Аналогично, изменение положения по оси Y равно:
Допустим, что нужно вычислить величину суммарного перемещения по обеим осям X и Y. Иначе говоря, насколько далеко удалился мячик от исходного положения в центре рисунка? Это можно подсчитать на основе теоремы Пифагора, т.е. выполнить следующие вычисления:
Итак, величина перемещения мячика равна 5 метрам.
Согласно теореме Пифагора, сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.
Измеряем скорость
В предыдущих разделах рассматривалось движение в одном или двух пространственных измерениях. Однако реальные перемещения происходят за некоторый промежуток времени, т.е. с некоторой скоростью. Например, за какое время произошло перемещение на рис. 3.1 из исходного положения в конечное положение: за 12 лет или 12 секунд?
Остальная часть этой главы посвящена измерению скорости перемещений. Аналогично измерению перемещения в пространстве, можно измерять разницу во времени между началом и концом движения, которая обычно выражается следующим образом:
Здесь \( t_1 \) обозначает конечное время, \( t_0 \) — начальное время, а их разность — количество времени, необходимого для перемещения, например движения мячика от начального к конечному положению. Когда ученые хотят узнать, насколько быстро происходит это событие, то фактически это значит, что они хотят измерить скорость.
Подробнее о скорости: что же это такое
Наверняка вам известно из опыта, что скорость определяется следующим образом:
Например, если расстояние \( s \) пройдено за время \( t \) , то скорость \( v \) равна:
Переменная \( v \) обозначает только величину скорости, но истинная скорость также имеет направление (более подробно это описывается в главе 4). Иначе говоря, скорость является вектором (векторы обычно обозначаются полужирным начертанием, например \( \mathbf
\) ). Векторы обладают величиной и направлением, т.е., зная скорость, мы знаем не только быстроту, но и направление движения. Аналогично, перемещение в более общем смысле является вектором, т.е. характеризуется не только величиной, но и направлением смещения (более подробно векторы описываются в главе 4).
Достаточно просто, не так ли? Точнее говоря (физики очень любят точность), скорость равняется изменению положения, деленному на изменение времени. Потому скорость движения вдоль оси X можно выразить следующим образом:
В реальном мире скорость может принимать очень разные формы, некоторые из них описываются в следующих разделах.
Смотрим на спидометр: мгновенная скорость
Итак, у нас уже есть общее представление о скорости. Именно ее измеряет спидометр автомобиля, не так ли? Когда вы катите по прямолинейному шоссе, все, что нужно делать, — всего лишь следить за показаниями спидометра. “Уже 140 километров в час. Пожалуй, сбросим скорость до 120”. Именно так мы часто поступаем в жизни, а иначе говоря, так мы определяем мгновенную скорость.
Понятие мгновенной скорости играет важную роль в понимании физических процессов. В данный момент времени спидометр показывает 120 километров в час, значит, ваша мгновенная скорость равна именно этой величине. Если вы ускоритесь до 150 километров в час, то ваша мгновенная скорость станет равной этой новой величине. Мгновенная скорость — это скорость в данный момент времени. Спустя две секунды мгновенная скорость может стать совершенно другой.
Движемся постоянно: равномерная скорость
А что если долгое время автомобиль едет со скоростью 120 километров в час? В физике эта скорость называется равномерной (или постоянной), а в жизни она возможна только при движении на абсолютно ровных и прямолинейных дорогах, когда долгое время можно поддерживать движение без изменения скорости.
Равномерное движение с постоянной скоростью является простейшим видом движения, поскольку оно никак не меняется.
Движемся вперед и назад: неравномерное движение
Название этого типа движения говорит само за себя: неравномерное движение означает движение со скоростью, меняющейся со временем. Именно с такой скоростью мы чаще всего сталкиваемся в повседневной жизни. Вот как выглядит уравнение изменения скорости от исходной скорости \( v_1 \) до конечной скорости \( v_0 \) :
Остальная часть этой главы посвящена ускорению, которое характеризует неравномерность движения.
Жмем на секундомер и определяем среднюю скорость
Выражение со скоростями не так уж неосязаемо, как может показаться. Измерения скорости можно сделать более конкретными. Допустим, что вам хочется совершить путешествие из Нью-Йорка в Лос-Анджелес, которые находятся на расстоянии около 2781 миль друг от друга. Если предположить, на это путешествие ушло 4 суток, то какой была ваша скорость?
Скорость можно найти, если поделить пройденное расстояние на затраченное на это время:
Итак, результат 695,3 получен, но в каких единицах он выражен?
В этом выражении мили делятся на сутки, т.е. результат равен 695,3 милям в сутки. Это не совсем стандартная единица измерений и вполне естественно было бы поинтересоваться: а сколько это миль в час? Для ответа на этот вопрос нужно перевести сутки в часы, как показано в главе 2. Поскольку в сутках 24 часа, то получим следующий результат:
Итак, получен более понятный результат 28,97 миль в час. Смущает лишь столь малая величина скорости, ведь обычно машины едут со скоростью в 2-3 раза быстрее, однако среднюю скорость для всего путешествия мы вычислили, разделив все расстояния на все время, включая время отдыха.
Средняя скорость и неравномерное движение
Средняя скорость отличается от мгновенной, если только вы не движетесь равномерно, когда скорость вообще не меняется. А средняя скорость неравномерного движения, когда все расстояние делится на все время, может отличаться от мгновенной скорости.
Путешествуя из Нью-Йорка в Лос-Анджелес, вам наверняка придется провести несколько ночей в отелях, и во время вашего отдыха мгновенная скорость автомобиля равна 0 миль в час, а средняя скорость — 28,97 миль в час! Дело в том, что средняя скорость получена в результате деления всего расстояния на все время.
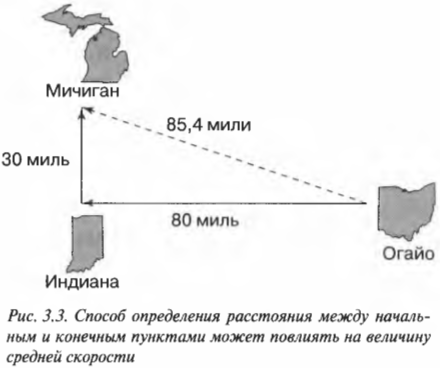
Средняя скорость может зависеть от фактически пройденного пути. Допустим, что, путешествуя по штату Огайо, вы решили подвезти попутчика в штат Индиана и погостить у вашей сестры в штате Мичиган. Все путешествие может иметь вид, показанный на рис. 3.3: первые 80 миль — в штат Индиана, а потом 30 миль — в штат Мичиган.
Если ехать со скоростью 55 миль в час, то для преодоления всего пути длиной 80 + 30 = 110 миль потребуется 2 часа. Но если взять расстояние по прямой между начальной и конечной точкой путешествия, которое равно 85,4 миль, то средняя скорость будет равна:
Таким образом, получена средняя скорость для расстояния от начальной до конечной точки путешествия вдоль пунктирной линии. Но если вам нужно определить скорость для каждого из двух отрезков фактически пройденного пути, то нужно измерить длину каждого из двух отрезков и разделить их на время их прохождения.
При движении с равномерной скоростью это можно сделать легко и просто, поскольку в таком случае средняя скорость равняется мгновенной скорости в любой точке пути.
Изучая движение, нужно учитывать не только скорость, но и направление движения. Именно по этой причине огромное значение имеет понятие вектора скорости. Более подробно векторы описываются в главе 4.
Ускоряемся и замедляемся
Как и в случае со скоростью, вам уже наверняка знакомо понятие ускорения. Ускорение характеризует быстроту изменения скорости. При выезде с подземной парковки порой приходится слышать визг шин — кто-то пытается ускориться, подрезать и обогнать вас на выезде. Вот он проскакивает перед вами буквально в нескольких сантиметрах и резко тормозит прямо перед вами, принуждая вас резко нажать на педаль тормоза. Именно в таких ситуациях очень полезно и важно знать основы физики.
Определяем ускорение
С точки зрения физики ускорение ( \( a \) ) — это изменение скорости ( \( \Delta v \) ) за единицу времени ( \( \Delta t \) ):
Это соотношение можно переписать иначе для известных начальной и конечной скоростей в начальный и конечный моменты времени соответственно:
Определяем единицу ускорения
Единицу ускорения можно легко определить, если проанализировать определение ускорения, в котором изменение скорости делится на изменение времени:
Подставляя единицы измерения, получим:
Итак, единица ускорения — это единица расстояния, деленная на единицу времени в квадрате. Иначе говоря, ускорение — это скорость изменения скорости.
Поскольку ускорение — это расстояние, деленное на время в квадрате, то среди единиц измерения можно встретить следующие: километр на секунду в квадрате, метр на секунду в квадрате, сантиметр на секунду в квадрате, миля на секунду в квадрате, фут на секунду в квадрате и т.д.
Шутки ради допустим, что вы едете со скоростью 75 миль в час и в зеркале заднего вида видите проблесковый маячок дорожного патруля. Жмете на тормоза и останавливаетесь спустя 20 секунд. Инспектор дорожного патруля подходит к вам и сообщает: “Выдвигались со скоростью 75 миль в час в зоне, где скорость движения ограничена величиной 30 миль в час”. Что можно ответить? Попробуйте поразить воображение инспектора своими познаниями физики.
Быстро подсчитайте величину своего замедления после сигнала инспектора, чтобы поразить его своим исключительным законопослушанием! Достаньте калькулятор и начните вводить в него данные. Преобразуйте величину скорости 75 миль в час в более впечатляющие единицы измерения, например в сантиметры в секунду. Для этого сначала преобразуйте единицу измерения скорости, т.е. выразите ее в милях в секунду:
Теперь попробуем преобразовать мили в секунду в более впечатляющие для инспектора единицы измерения, например в сантиметры в секунду. Как известно, 1 миля содержит 5280 футов, а 1 фут — 12 дюймов. Тогда пройденное расстояние в дюймах в секунду равно:
В главе 2 уже упоминалось, что 1 дюйм равен 2,54 сантиметрам, потому пройденное расстояние в сантиметрах в секунду равно:
Таким образом исходная скорость движения была равна 3,4⋅10 3 сантиметров в секунду, а конечная — 0 сантиметров в секунду. Это изменение скорости произошло за 20 секунд. Так чему же равняется ускорение? Напомним еще раз формулу ускорения:
Подставляя числа, получим:
Конечная скорость равна 0 см/с, а исходная — 3,4⋅10 3 см/с, так что подставляя значения в эту формулу, получим:
Аналогично скорости, ускорение может принимать разный вид в разных физических задачах. Ускорение может быть положительным, отрицательным, средним, мгновенным, равномерным или неравномерным. В следующих разделах описываются некоторые такие ситуации.
Положительное и отрицательное ускорение
При решении физических задач всегда нужно внимательно следить за знаком используемой величины. Ускорение, как и скорость, может быть отрицательным или положительным. При торможении автомобиля его скорость меняется с положительной до 0, а потому ускорение имеет отрицательный знак.
Ускорение, как и скорость, обладает знаком.
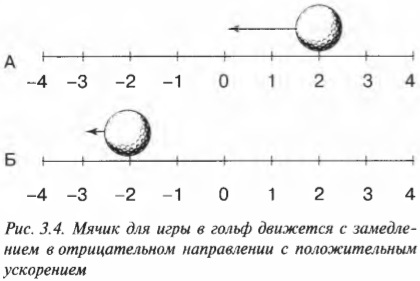
Не следует думать, что отрицательное ускорение всегда означает замедление, а положительное ускорение всегда означает ускорение. На рис. 3.4 показан пример ситуации, когда мячик для игры в гольф движется с замедлением из начального положения (схема А на рис. 3.4) в конечное положение (схема Б на рис. 3.4), но с положительным ускорением.
Поскольку отрицательная величина скорости уменьшается, то в целом ускорение мячика имеет положительную величину. Иначе говоря, для уменьшения отрицательной скорости нужно сделать положительное приращение скорости, т.е. ускорение при этом будет положительным.
Знак ускорения сообщает нам о том, как меняется скорость. Положительное ускорение означает, что скорость увеличивается в положительном направлении и уменьшается в отрицательном направлении. И наоборот, отрицательное ускорение означает, что скорость увеличивается в отрицательном направлении и уменьшается в положительном направлении.
Среднее и мгновенное ускорение
Аналогично скорости, ускорение может иметь мгновенное или среднее значение. Среднее ускорение равно отношению изменения скорости к изменению времени. Среднее ускорение обозначается штрихом сверху, \( \overline \) , и вычисляется аналогично средней скорости, т.е. от конечной скорости отнимается начальная скорость и полученная разность делится на все время (т.е. на разность конечного и начального времени):
Это соотношение дает нам среднее ускорение, но фактическое ускорение в произвольный момент времени не всегда равно среднему ускорению. Например, в предыдущем примере после того, как вы заметили сигнал инспектора, вы очень сильно нажимаете педаль тормоза, и автомобиль тормозит с очень большим ускорением. Но перед самой остановкой вы отпускаете педаль тормоза, и ваш автомобиль тормозит с уже меньшим ускорением. Оба эти мгновенные значения отличаются от величины среднего ускорения, вычисленного после деления всего изменения скорости на все время торможения.
Равномерное и неравномерное ускорение
Движение с неравномерным ускорением означает движение с изменением ускорения. Например, при движении в городе часто приходится тормозить перед знаками и сигналами остановки движения, а потом снова разгоняться.
Однако существуют ситуации, когда ускорение остается неизменным во время движения, например ускорение свободного падения под действием силы притяжения Земли. Это ускорение в общем случае равно 9,8 метров в секунду в квадрате, направлено к центру Земли и неизменно.
Связываем ускорение, время и перемещение
Итак, в этой главе вы познакомились с четырьмя параметрами движения: ускорением, скоростью, временем и перемещением. Перемещение и время связаны следующим простым соотношением для скорости:
Аналогично, скорость и время связаны следующим простым соотношением для ускорения:
Однако эти соотношения связывают только по два “уровня” переменных, т.е. скорость с перемещением и временем, а ускорение со скоростью и временем. А как связать три “уровня” переменных, т.е. ускорение со временем и перемещением?
Допустим, что вы участвуете в гонке и после пробного заезда хотели бы знать ускорение, которое способен обеспечить ваш автомобиль по известному пройденному пути 402 метра за 5,5 секунд. Таким образом, получается задача, в которой нужно связать ускорение с перемещением и временем.
Итак, для решения этой задачи нужно вывести уравнение связи ускорения с перемещением и временем.
Не такие уж и далекие связи
Попробуем связать ускорение, перемещение и время, жонглируя разными переменными, пока не получим нужный результат. Перемещение равно средней скорости, умноженной на время:
Итак, у нас есть отправная точка. Какова средняя скорость автомобиля из предыдущего примера? Начальная скорость была равна 0, а конечная — очень большой. Поскольку ускорение было постоянным, то скорость росла линейно от нуля до конечного значения (рис. 3.5).
При постоянном ускорении средняя скорость равна половине суммы конечной и начальной скоростей:
Конечная скорость равна:
Тогда средняя скорость равна:
Теперь подставим это выражение для средней скорости в уравнение для перемещения \( s=\overline
Теперь вместо переменной \( t \) можно подставить исходную разность конечного и начального моментов времени и получим:
Ура! Мы вывели одно из наиболее важных соотношений между ускорением, перемещением, временем и скоростью, которые используются в физических задачах.
Выводим более сложные соотношения
А что если движение началось не с нулевой начальной скоростью? Как в таком случае связать ускорение, время и перемещение? Как такое начальное значение скорости, например 100 миль в час, повлияет на величину пройденного расстояния? Поскольку расстояние равно скорости, умноженной на время, то искомое соотношение имеет следующий вид:
Такое выражение не так уж и легко запомнить, если, конечно, вы не обладаете фотографической памятью. Сложно даже запомнить более простую формулу связи между перемещением и временем для движения с постоянным ускорением, с нулевого начального момента и с нулевой начальной скоростью:
Если движение начинается не с нулевой скоростью, то к предыдущему выражению нужно добавить расстояние, которое было бы пройдено за то же время с начальной скоростью. Подобные соображения на основе здравого смысла значительно упрощают решение физических задач. Механическое запоминание формул без понимания их смысла не всегда поможет вам найти ошибку в вычислениях.
Так каким же было ускорение автомобиля в одном из предыдущих примеров? Теперь мы знаем, как связаны перемещение, ускорение и время, и для ответа на этот вопрос нужно применить алгебраические навыки. Итак, мы имеем:
После деления обеих частей на \( t^2 \) и умножения на 2 получим:
Великолепно! Подставляя числа, получим:
Итак, получилось, что ускорение автомобиля равно 27 метров в секунду в квадрате. Насколько велико это ускорение? Например, ускорение свободного падения в поле тяготения Земли, \( g \) , равно около 9,8 метров в секунду в квадрате, т.е. ускорение автомобиля приблизительно равно \( 2,7g \) .
Связываем скорость, ускорение и перемещение
До сих мы достаточно успешно справлялись со всеми предложенными задачами. А что если немножко усложнить их условия? Допустим, что в примере с автомобилем вам известно только ускорение 26,3 метров в секунду в квадрате и конечная скорость 146,3 метров в секунду, а нужно определить пройденное расстояние. Справитесь ли вы с таким заданием? Внимательный читатель уверенно ответит: “Никаких проблем, только дайте мне калькулятор”.
Прежняя задача в новой формулировке кажется более сложной, поскольку в прежних соотношениях всегда присутствовало время. Это значит, что, зная время движения, вы легко сможете решить задачу даже в новой более сложной формулировке. Чтобы определить время движения, достаточно знать ускорение, а также начальную и конечную скорости.
то получим выражение для времени движения:
Теперь, зная время, можно определить пройденное расстояние по формуле:
Второй член можно исключить, потому что \( v_0 \) = 0. Итак, после подстановки чисел получим:
Как выглядит формула связи перемещения, ускорения и скорости? Для ее получения нужно найти выражение для времени движения:
Подставляя в эту формулу выражение для времени движения, получим:
После несложных алгебраических преобразований получим:
Перемещая член \( 2a \) в другую часть уравнения, получим еще одно важное соотношение, которое связывает скорость, ускорение и перемещение:
Уф, это выражение стоит запомнить!
После решения всех этих задач каждый читатель по праву может считать себя повелителем движения.