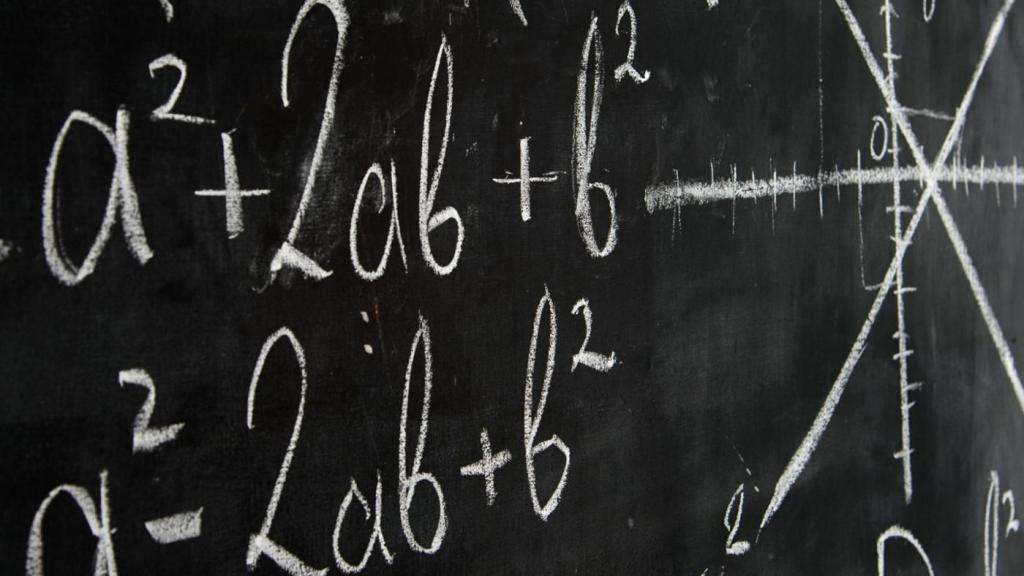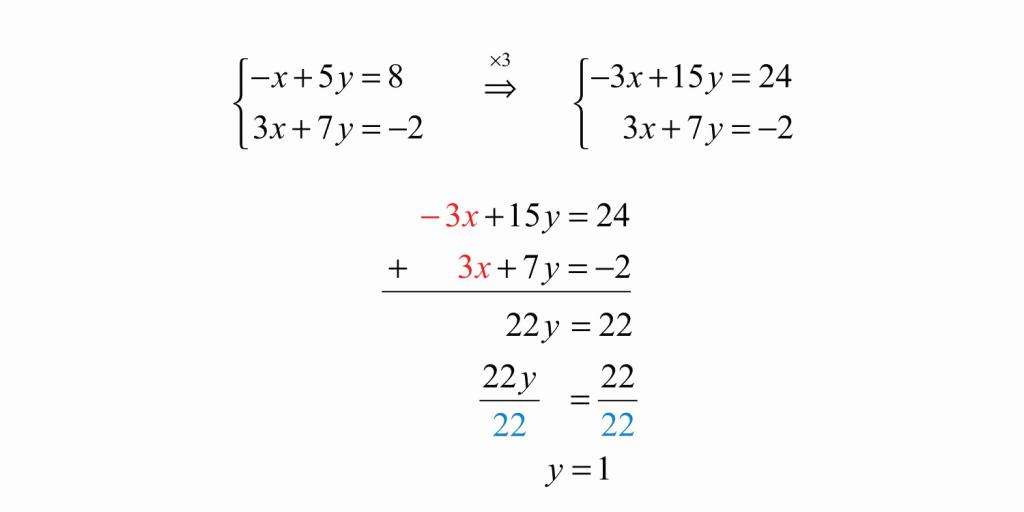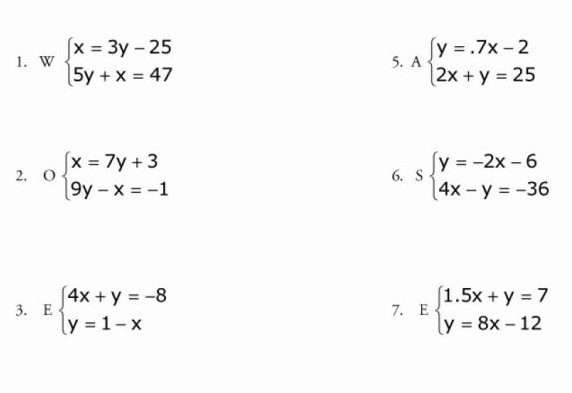Что означает переменная k чему она равна
Что означает переменная «k»?
Я использую библиотеку tween.js, она содержит некоторые встроенные функции ослабления, такие как эта:
Руководство пользователя описывает переменную k как:
- k : прогресс ослабления или насколько далеко по длительности мы находимся. Допустимые значения находятся в диапазоне [0, 1].
Мой вопрос: зачем, k чему это письмо? Если бы я сам написал эту функцию, я бы назвал ее p означающей прогресс или процент.
В этой статье в Википедии об условных обозначениях в математике (https://en.m.wikipedia.org/wiki/Latin_letters_used_in_mathematics) говорится, что нижний регистр k представляет собой:
• постоянную Больцмана, это часто представляется как kB, чтобы избежать путаницы с
• Волновое число волнового уравнения
• целое число, например, фиктивная переменная в суммировании, или индекс матрицы.
• неопределенная (действительная) константа
• весенняя константа закона Гука
• кривизна пространства-времени из уравнений Фридмана в космологии
Я бы предположил, что четвертый элемент является наиболее подходящим описанием k в этом случае.
целое число, например, фиктивная переменная в суммировании, или индекс матрицы.
Если у автора есть причина назвать переменную k возможно, это она. Если это так, то «k» не означает «что-то», а просто является соглашением, используемым матовскими ботаниками;)
Что означает переменная «k»?
В руководстве пользователя переменная k описывается следующим образом:
2 ответа
В этом коде я пытаюсь сделать так, чтобы первый параметр в моей рабочей функции go был типом ‘type family’. Я вижу, что в документации type type families аналогичная функция insert принадлежит классу type, в то время как в моем примере ниже она этого не делает. Я новичок в семействах типов, так.
Возможный Дубликат : Что означает префикс ‘k’ в Apple’s APIs? Objective C-почему константы начинаются с k Например, коды результатов, определенные для служб аудиоформата : kAudioFormatUnspecifiedError kAudioFormatUnsupportedPropertyError и т.д. Что означает это ведущее к? Я всегда.
Эта статья Википедии о соглашениях об именах в математике ( https://en.m.wikipedia.org/wiki/ Latin_letters_used_in_mathematics ) говорит нам, что нижний регистр k представляет:
• префикс единицы измерения кило- (103)
• постоянная Больцмана, ее часто представляют как kB, чтобы избежать путаницы с
•волновое число волнового уравнения
•целое число, например, фиктивная переменная в суммировании или индекс матрицы.
•неопределенная (реальная) константа
•константа spring закона Гука
•кривизна пространства-времени из уравнений Фридмана в космологии
Я бы предположил, что четвертый пункт является наиболее подходящим описанием k в данном случае.
целое число, например, фиктивная переменная в суммировании или индекс матрицы.
Похожие вопросы:
Вот пример кода в c, я не уверен, что означает условие k & 1. int k,i,c; k = i >> c; if (k & 1) printf(1); else printf(0);
Что такое переменные? Переменная величина в математике
Итак, в этой статье пойдет речь о том, что такое переменные, об их видах и свойствах. Также будут рассмотрены разные математические выражения: неравенства, формулы, системы и алгоритмы их решения.
Понятие переменной
Вам будет интересно: Плотность осмия: характеристика, значение, физические и химические свойства, получение и применение
Вам будет интересно: Российская таможенная академия в Москве: описание, адрес, факультеты.
Виды величин
Вам будет интересно: Конспект урока русского языка во 2 классе. Правила «жи – ши», «ча – ща», «чу – щу»
Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).
Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.
История
История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.
Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.
С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:
За x2 принимаем некое k, и уравнение приобретает понятный вид:
Вот какую пользу в математику несет введение переменных.
Неравенства, примеры решения
Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.
Вам будет интересно: Французские местоимения: типы и виды
Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:
Пример с одной переменной:
Делим обе части неравенства на 10 и получаем:
Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.
Решением этого неравенства будет промежуток (20; +∞).
Решение нестрогого неравенства осуществляется так же, как и строгого:
Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.
Квадратные неравенства
Если взять квадратное уравнение вида ax2 + bx +c = 0 и изменить в нем знак равно на знак неравенства, то соответственно получим квадратное неравенство.
Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.
По формуле корней квадратного уравнения получаем:
Или можно было решить это уравнение по теореме Виета:
Методом подбора получаем такие же корни уравнения.
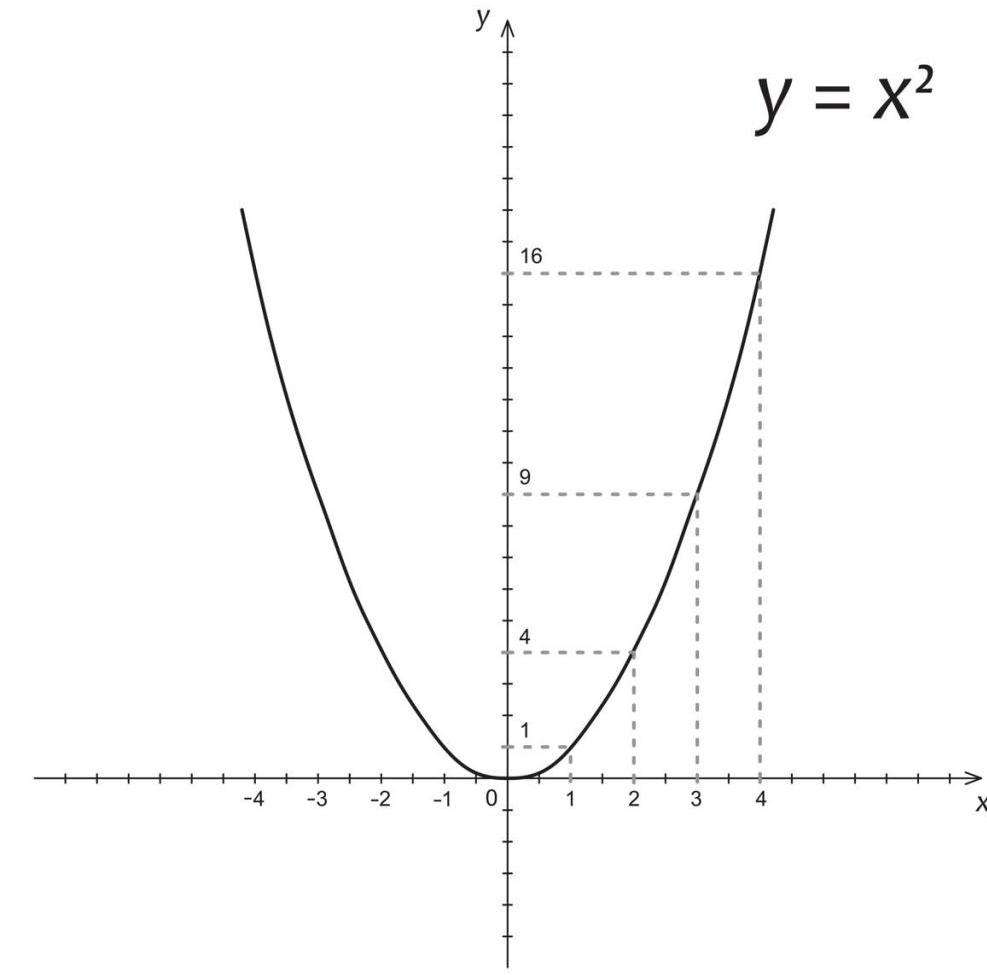
Парабола
1. Определяем, куда направлены ветви параболы.
2. Приравниваем функцию к нулю и находим корни уравнения.
3. Строим числовую прямую, отмечаем на ней корни, проводим параболу и находим нужный нам промежуток в зависимости от того, какой у неравенства знак.
Выписываем в виде функции:
Приравниваем к нулю.
Дальше решаем как квадратное уравнение и находим нули функции:
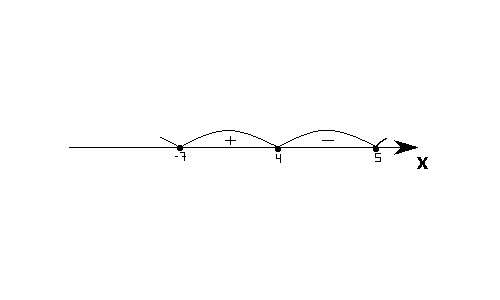
Метод интервалов
1. Находим корни уравнения, при которых неравенство равно нулю.
2. Отмечаем их на числовой прямой. Таким образом она делится на несколько интервалов.
3. Определяем знак любого интервала.
4. Расставляем знаки у остальных интервалов, меняя их через один.
2) Изображаем их на числовой прямой.
3) Определяем знаки интервалов.
2. Отмечаем их на числовой прямой.
3. Определяем знаки интервалов.
Далее, начиная от первого промежутка, расставляем знаки, меняя их через один.
Неравенство больше нуля, то есть надо найти множество положительных значений на прямой.
Системы уравнений
Системой уравнений с двумя переменными называют два уравнения, объединенных фигурной скобкой, для которых необходимо найти общее решение.
Системы могут являться равносильными, если общее решение одной из них является решением другой, или они обе не имеют решений.
Алгебраический метод
Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.
Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:
Решаем получившееся уравнение и находим икс.
Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:
Метод подстановки
Это, пожалуй, самый простой метод, в котором трудно совершить ошибку. Возьмем систему уравнений номер 1 с этой картинки.
В первой ее части икс уже приведен к нужному нам виду, поэтому нам остается только подставить его в другое уравнение:
Переносим число без переменной вправо, приводим подобные слагаемые к общему значению и находим игрек:
Затем, как и в алгебраическом методе, подставляем значение игрека в любое из уравнений и находим икс:
График линейной функции, его свойства и формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Информатика 9 класс Помогите плиз выбрать правильные ответы
1.Основными компонентами среды программирования являются:
1)символы языка, элементарные конструкции, выражения, операторы
2)редактор, компилятор, редактор
3)процедуры, функции
4.Какое выражение позволяет возвести число a в квадрат?
1.sqrt(a)
2.round(2,a)
3.exp(a*ln(2))
4.sqr(a)
5.abs(a,2)
5.Операция mod позволяет найти.
1)остаток от целочисленного деления
2)найти результат целочисленного деления одного числа на другое
3)результат деления одного числа на другое
4)нет правильного ответа
6.Что означает в Pascal точка с запятой?
1)конец программы
2)конец цикла
3)отделение операторов друг от друга
4)конец строки программы
7.Каким служебным словом описываются дробные переменные?
1)string
2)word
3)integer
4)real
5)char
11.В программе используется целочисленная переменная x. Выберите правильное описание этой переменной:
1.Var x:integer;
2 Var x:integer
3 Var x:Real;
4 Var x:String;
13Переменная k описана как целочисленная. Допустима ли в программе следующая команда?
k:=6/4;
1да
2нет
15Какое значение примет переменная z после выполнения фрагмента программы?
x:=144;
y:=sqrt(x)/(x-140);
z:=(x+y)/(200-53);
1)1
2)12
3)3,8
4)1,06
16.Укажите оператор цикла с известным число повторений.
1.while
2.for
3.if
4.repeat
17.Укажите оператор ветвления.
1.if
2.for
3.repeat
4.while