Что означает перевернутая галочка в информатике
Символ галочка ✔ где найти и как его поставить (2022)
Символ галочка не представлен отдельно на клавиатуре, поэтому сразу напечатать его не получится. Однако существует много ситуаций, когда в текст нужно его добавить. При помощи этого символа можно выделить самые важные мысли, пожелания или распоряжения. Ниже будет представлена подробная инструкция, как вставить этот символ в текстовый документ, сообщение или пост.
Зачем нужен символ «галочка»?
Обойтись без символа «птичка» возможно, однако с его помощью можно получить дополнительные преимущества в тексте:
Вставить символ галочка в документ “Word”
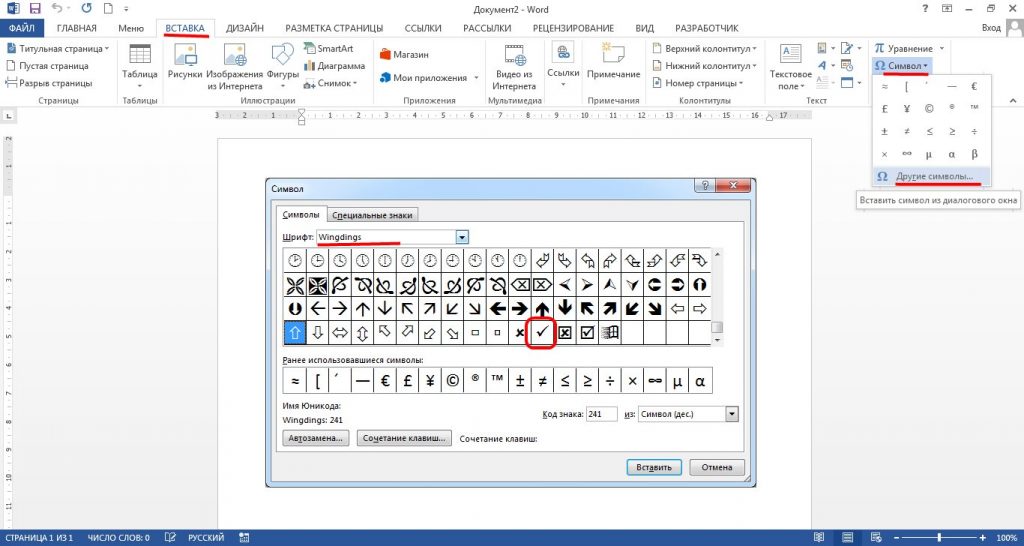
Наиболее простой способ поставить галочку в документе “Word” при помощи «Символов»:
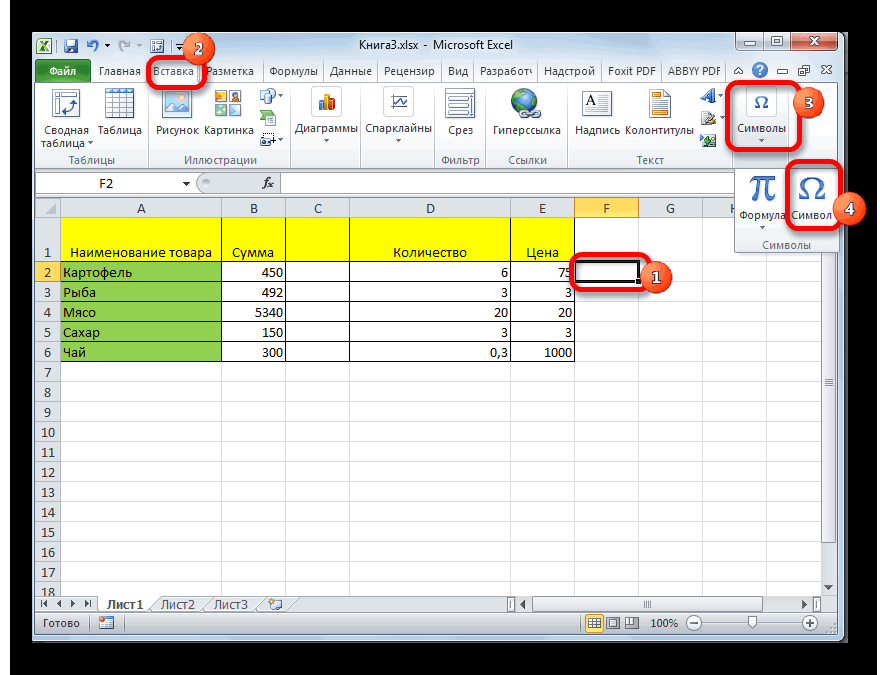
Вставить символ галочка в документ “Excel”
Поставить галочку в документе “Excel” можно двумя простыми способами:
Установка галочки в чекбоксе
Чтобы статус установки или устранения галочки запускал какие-то сценарии, следует установить чекбокс. В сравнении с предыдущими инструкциями, установка чекбокса несколько сложнее. Сам чекбокс имеет вид квадратика, в котором может находится или отсутствовать символ галочки. Для работы с чекбоксом, его следует установить в документ, так как по умолчанию эта функция отключена. Для начала нужно зайти во вкладку:
Справа в пункте «Основные вкладки» следует поставить галочку возле графы «Разработчик». Подтверждает действие нажатием кнопки «Ок». Теперь вкладка «Разработчик» находится в ленте меню документа.
Далее необходимо перейти в только что активированный «Разработчик» в меню ленты документа. Откроется окошко «Разработчика»:
Если Вам мешает надпись «Флажок» с цифрой, её можно удалить, предварительно выделив этот текст. Вместо этой надписи можно вставить нужную, а можно оставить только чекбокс. Если нужно установить много галочек, достаточно просто скопировать имеющийся и вставить в нужную ячейку.
Самый простой способ
Вставить символ «птичка» без любых сложностей за считанные минуты можно при помощи «Википедия». Совершить такое действие можно при помощи интернета в любом имеющемся браузере:
Автор, специалист в сфере IT и новых технологий.
Получил высшее образование по специальности Фундаментальная информатика и информационные технологии в Московском государственном университете имени М.В. Ломоносова. После этого стал экспертом в известном интернет-издании. Спустя время, решил попробовать писать статьи самостоятельно. Ведет популярный блог на Ютубе и делится интересной информацией из мира технологий.
Галочка в тексте символ
Галочка (используют также птичка или галка) — знак (✓, ✔, ☑, и так далее) для обозначения согласия или включения, учёта. Например, «да; проверено», «да; правильный ответ», «да; использовать», «исполнено/выполнено» и тому подобное. В избирательных бюллетенях для этих целей иногда используют крестик, но тот также может означать и «нет», «неверно».
Юникод [ править | править код ]
Юникод предоставляет несколько символов для галочки:
Плохая новость — символ галочка отсутствует на клавиатуре. Хорошая новость — есть возможность скопировать его прямо с этой страницы. А затем вставить во вконтакт, ворд или на список покупок от жены.
Этот текст также доступен на следующих языках: English;
Символ галочка не представлен на клавиатуре, но с помощью специальных комбинаций его можно легко добавить в ваше сообщение, пост или текстовый документ.
Рассмотрим детальнее, как это можно сделать.
Содержание:
Виды галочек + использование
Значок галочка (птичка, галка) – это специальный значок, который часто используется для описания подтверждения чего-либо.
Может встречаться в оформлении перечислений или подчеркиваний мысли. Прочитав следующие инструкции, найти и использовать символ вы сможете самостоятельно.
Самый простой вариант – это копирование объекта с этой статьи. Существует несколько видов значка:
Если вам понадобилась галка для использования в одном предложении или фразе, просто скопируйте понравившийся элемент с помощью его выделения и сочетания клавиш CTRL и C на клавиатуре.
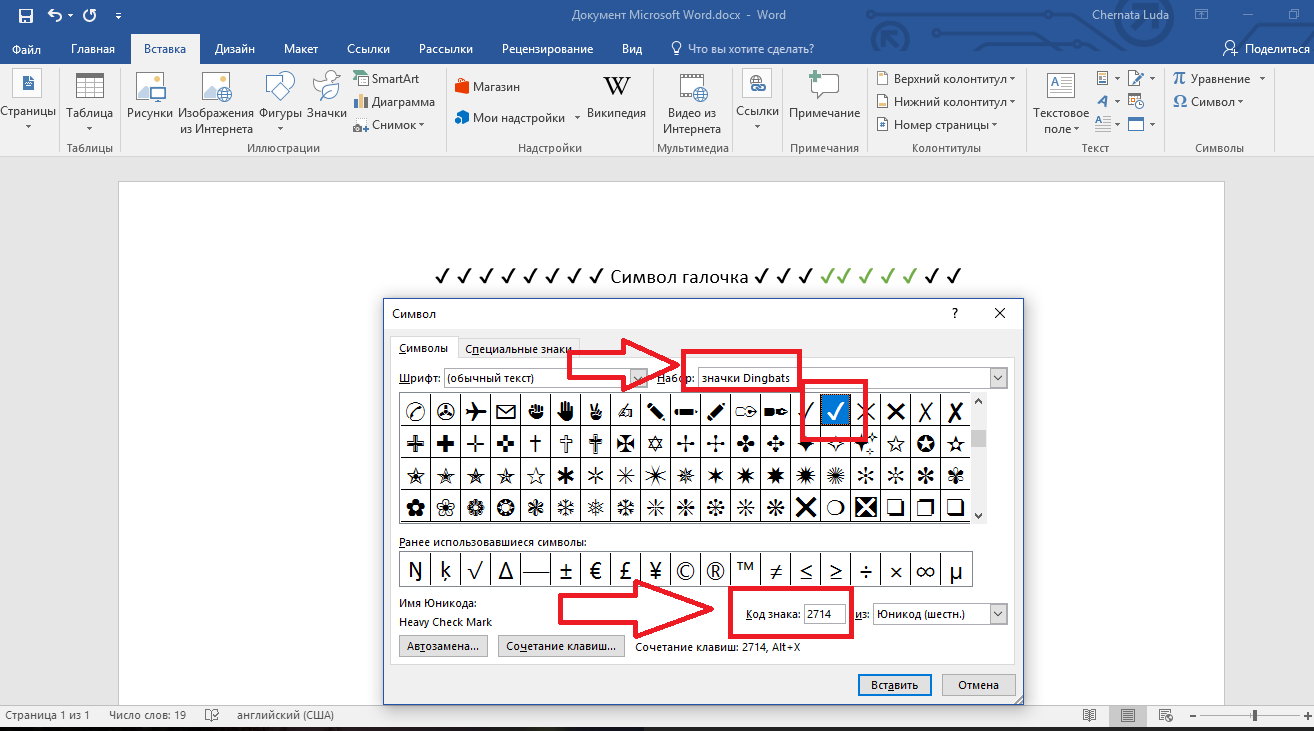
Цифровые обозначения для разных видов галочек бывают следующими: 2713 (обычный знак), 2714 (полужирный шрифт), 2705 (галочка в квадрате выделенная), 2611 (в квадрате обычная).
Если комбинация U + 2713 или другая не превращается автоматически в галочку, скорее всего, в документе не настроено автоматическое распознавание символов Юникода или вы вводите код неправильно.
В любом браузере текст сразу будет преображаться в нужный знак, поэтому вы можете смело набирать его в сообщениях и разных постах.
Читайте также:
Значок в MS Word
Все, кто хоть раз использовал текстовый редактор Ворд знают, что выставление специальных символов помогает структурировать документ и сделать его легко читаемым.
Значок галочки может понадобиться вам в процессе оформления списка задач, перечисления.
Неопытные пользователи выставляют знак с помощью добавления в документ изображения с нужным элементом. Такой подход неправильный, ведь он увеличивает конечный размер файла.
Все можно сделать гораздо проще. Чтобы поставить галку в Ворде, выполните несколько следующих шагов.
Рис.2 – главное окно в MS Word
Рис.3 – специальные символы в Ворде
После добавления галочки в тело документа вы сможете применить к ней любое форматирование: изменить цвет, шрифт, тип заголовка и прочие опции.
Вам это может быть интересно:
Видеоинструкции:
Как напечатать символ которого нет на клавиатуре
Естественно зная коды символов, можно печатать даже те из них, которых нет на клавиатуре. Для этого, удерживая клавишу ALT, набрать на цифровой клавиатуре код нужного символа, начиная с нуля. Вот примеры некоторых символов, и коды для их написания.
Как поставить галочку в Ворде?
Рассмотрим, как поставить галочку в Ворде. Для установки птички в Ворде потребуется использование не только меню «Символ», но и специального шрифта.
Символ Галочка: как легко найти и проставить [Простая инструкция]
Так называемый символ Галочка необходим в ряде случаев при оформлении текста.
В частности, используется для подтверждения согласия (на обработку данных, на участие и т. д.), указания верного варианта ответа и во многих других случаях.
Какой бывает символ галочка, как его поставить в документах, сообщения и постах в интернете рассказано в данном материале.
Содержание:
Виды значка
Какие же бывают галочки? В зависимости от общего стиля текста, его типа оформления, повода для проставления символа, вы можете выбрать тот или иной ее тип:
Если речь идет об использовании смайликов (с телефона, в социальной сети), то галочка также может быть цветной (того или иного оттенка в зависимости от типа операционной системы).
Используется символ, чаще всего, следующим образом:
Ниже в материале рассмотрены способы проставления того или иного типа знака.
В Word
Копирование
Наиболее простой способ проставления нужного вам символа – копирование его из этого материала.
Установите курсор мыши слева от символа, зажмите левую клавишу и выделите его.
Затем нажмите Ctrl+C для копирования, а затем установите курсор на нужное место и нажмите Ctrl+V для вставки символа.
Это способ наиболее простой и быстрый, но он подходит только для разовой вставки символа. Если же он требуется вам достаточно часто, то используйте другие методы.
Ресурсы системы
Символ можно пропечатать вручную прямо с клавиатуры, введя знак U+, а затем код галочки.
Однако такой подход работает только в браузерах и на тех операционных системах, в которых настроено распознавание Юникода.
По умолчанию такая функция бывает недоступна, настраивать ее приходится достаточно долго и сложно, да и не все пользователи знают, как это делать.
Потому куда проще применить специальный символ в Ворд.
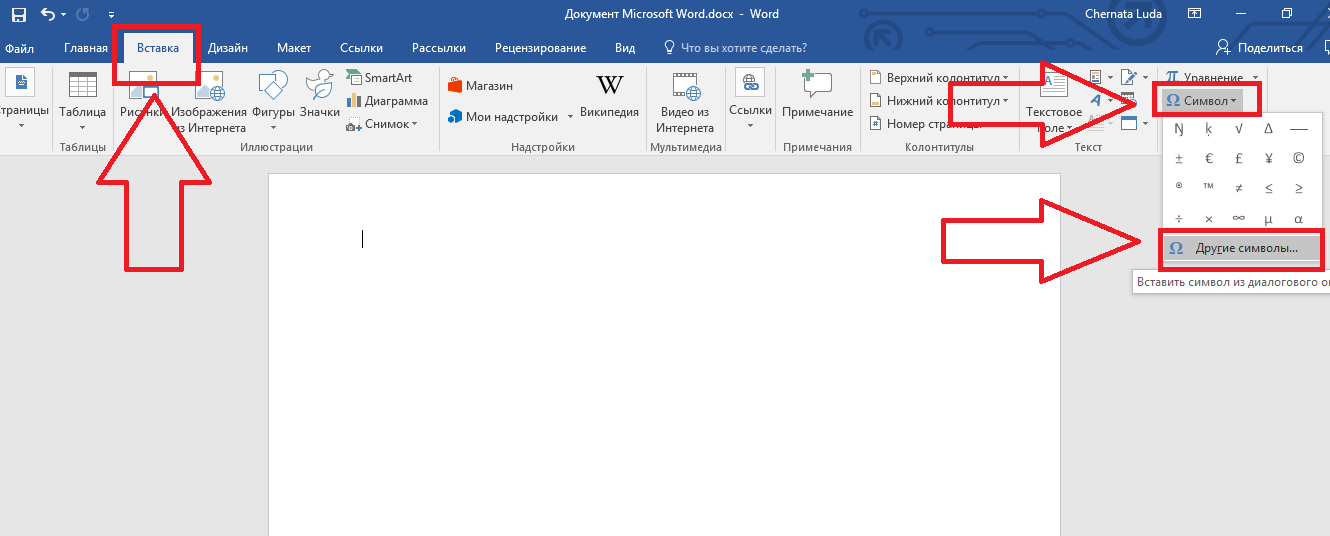
Для того, чтобы это сделать, следуйте алгоритму:
Рис. 4 Другие символы
Если галочка добавлена в документ таким образом, то она полностью функциональна и может подвергаться всем тем же изменениям и модификациям, что и текст в документе.
Вы можете изменять ее цвет, размер, шрифт, выделять и прочее.
В браузере
Так как абсолютно все браузеры распознают 16-тиричную кодировку Юникод, вы можете добавлять галочки к тексту следующим образом:
Метод работает на абсолютно любой стадии интернет-активности – размещении поста, ответа на сообщение и прочее.
Цифровые обозначения символов таковы:
При хорошем знании символов и высокой скорости печати использовать такой метод ввода оказывается даже быстрее, чем искать символ в смайликах.
Читайте также:
Смайлики
Множество вариантов галочек скрыто в смайликах на Андроид и iOS.
Они находятся в разделе Символы и может быть выполнена в разных цветах, в зависимости от типа операционной системы.
При наборе сообщений в социальных сетях, чаще всего, также присутствует такой знак, и он также перенесен в раздел Символы или Специальные обозначения.
А чтобы не искать знак целенаправленно вы всегда можете скопировать код смайла.
Вывод
Существует множество способов проставить такой символ в тексте документа, сообщения.
В зависимости от того, насколько часто он вам требуется, вы можете выбрать тот или иной удобный для вас способ.
Компьютерщик рассказывает и показывает как быстро и просто научиться ставить крутейшие символы при помощи двух рук и клавиатуры 🙂
Галочка вверх в информатике
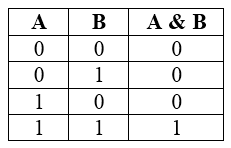
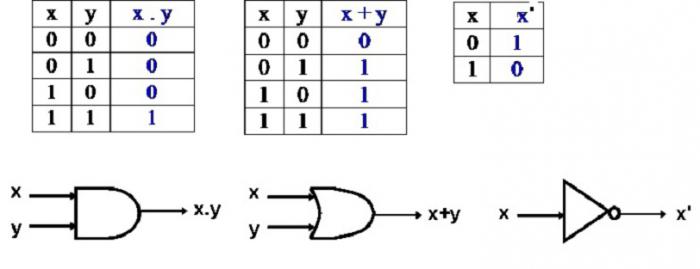
Конъюнкция или логическое умножение (в теории множеств – это пересечение)
Конъюнкция является сложным логическим выражением, которое истинно в том и только том случае, когда оба простых выражения являются истинными. Такая ситуация возможно лишь в единственном случае, во всех остальных случаях конъюнкция ложна.
Таблица истинности для конъюнкции
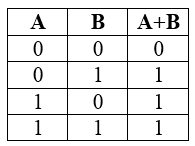
Дизъюнкция или логическое сложение (в теории множеств это объединение)
Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все выражения ложны.
Попробуй обратиться за помощью к преподавателям
Таблица истинности для дизъюнкции
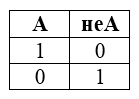
Отрицание, логическое отрицание или инверсия (в теории множеств это отрицание)
Отрицание – означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО и в итоге получаем, что если исходное выражение истинно, то отрицание исходного – будет ложно и наоборот, если исходное выражение ложно, то его отрицание будет истинно.
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Таблица истинности для инверсии
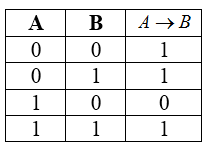
Импликация или логическое следование
Импликация – это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть, данная логическая операция связывает два простых логических выражения, из которых первое является условием ($A$), а второе ($A$) является следствием условия ($A$).
Таблица истинности для импликации
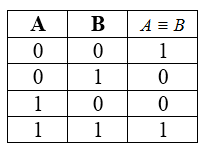
Эквивалентность или логическая равнозначность
Таблица истинности для эквивалентности
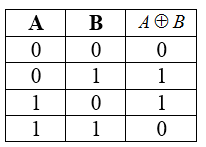
Строгая дизъюнкция или сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)
Строгая дизъюнкция истинна, если значения аргументов не равны.
Таблица истинности для операции сложения по модулю два
Свойства строгой дизъюнкции:
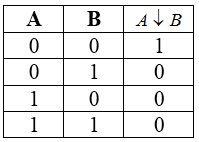
Стрелка Пирса
Таблица истинности для стрелки Пирса
Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:
$X downarrow X = ¬X$— отрицание
$(X downarrow Y) downarrow (X downarrow Y) equiv X vee Y$ — дизъюнкция
$(X downarrow X) downarrow (Y downarrow Y) equiv X wedge Y$ — конъюнкция
$((X downarrow X) downarrow Y) downarrow ((X downarrow X) downarrow Y) = X o Y$ — импликация
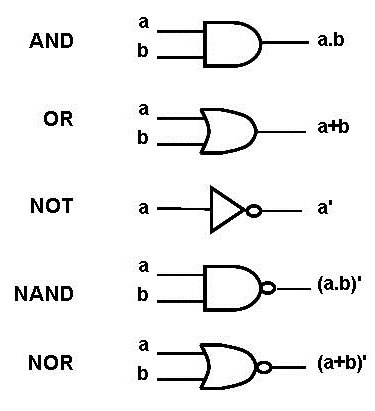
В электронике стрелка Пирса представлена в виде элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NОR).
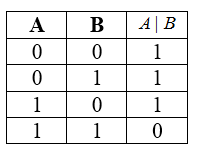
Штрих Шеффера
Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.
Таблицей истинности для функции штрих Шеффера
Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,
Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).
Порядок выполнения логических операций в сложном логическом выражении
Для того чтобы изменить указанный порядок выполнения логических операций, необходимо использовать скобки.
Общие свойства
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
Каждого, кто начинает изучать информатику, учат двоичной системе исчисления. Именно она используется для вычисления логических операций. Рассмотрим ниже все самые элементарные логические операции в информатике. Ведь если задуматься, именно они используются при создании логики вычислительных машин и приборов.
Отрицание
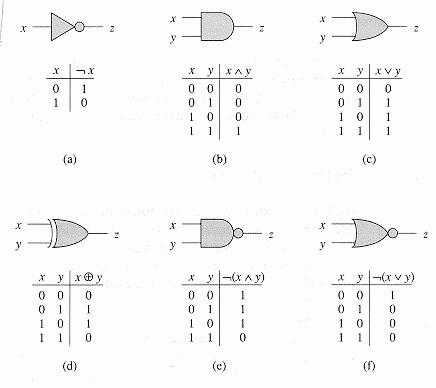
Перед тем как начать подробно рассматривать конкретные примеры, перечислим основные логические операции в информатике:
Также перед началом изучения логических операций стоит сказать, что в информатике ложь обозначается «0», а правда «1».
Каждое действие возможно описать либо цифрами 1/0, либо просто логическими выражениями. Начнём рассмотрение математической логики с простейшей операции, использующей всего одну переменную.
Логическое отрицание – операция инверсии. Суть заключается в том, что если исходное выражение – истина, то результат инверсии – ложь. И наоборот, если исходное выражение – ложь, то результатом инверсии станет – правда.
При записи этого выражения используется следующее обозначение «¬A».
Приведём таблицу истинности – схему, которая показывает все возможные результаты операции при любых исходных данных.
То есть, если у нас исходное выражение – истина (1), то его отрицание будет ложным (0). А если исходное выражение – ложь (0), то его отрицание – истина (1).
Сложение
Оставшиеся операции требуют наличия двух переменных. Обозначим одно выражение –
Для краткости создадим таблицу истинности.
Умножение
Разобравшись с операцией сложения, переходим к умножению (конъюнкции). Воспользуемся теми же обозначениями, которые были приведены выше для сложения. При письме логическое умножение обозначается значком «&», либо буквой «И».
Следствие
Логическая операция следования (импликация) – одна из простейших в математической логике. Она основана на единственной аксиоме – из правды не может следовать ложь.
Для облегчения выполнения математических действий также приведём таблицу истинности.
Равенство
Последней рассмотренной операцией станет логическое тождественное равенство или эквивалентность. В тексте оно может обозначаться как «. тогда и только тогда, когда. «. Исходя из этой формулировки, напишем примеры для всех исходных вариантов.
Свойства
Итак, рассмотрев простейшие логические операции в информатике, можем приступить к изучению некоторых их свойств. Как и в математике, у логических операций существует свой порядок обработки. В больших логических выражениях операции в скобках выполняются в первую очередь. После них первым делом подсчитываем все значения отрицания в примере. Следующим шагом станет вычисление конъюнкции, а затем дизъюнкции. Только после этого выполняем операцию следствия и, наконец, эквивалентности. Рассмотрим небольшой пример для наглядности.
Порядок выполнения действий следующий.
Для того чтобы решить этот пример, нам потребуется построить расширенную таблицу истинности. При её создании помните, что столбцы лучше располагать в том же порядке, в каком и будут выполняться действия.
Как мы видим, результатом решения примера станет последний столбец. Таблица истинности помогла решить задачу с любыми возможными исходными данными.
Заключение
В этой статье были рассмотрены некоторые понятия математической логики, такие как информатика, свойства логических операций, а также – что такое логические операции сами по себе. Были приведены некоторые простейшие примеры для решения задач по математической логике и таблицы истинности, необходимые для упрощения этого процесса.
что означает знак в информатике
Автор Semak задал вопрос в разделе Другие языки и технологии
что означает этот знак в информатике? и получил лучший ответ
Ответ от Василий Кравец[новичек]
этим знаком обозначается конъюнкция, или логическое умножение конъюнкция истинна (равна 1), когда все элементы умножения истинны если хотя бы один из элементов ложен (равен 0), то и все произведение ложно
Логика
НЕКОТОРЫЕ
СВОЙСТВА ЛОГИЧЕСКИХ ОПЕРАЦИЙ
1. Обозначения
1.1. Обозначения для логических связок (операций):
a) отрицание (инверсия, логическое НЕ) обозначается ¬ (например, ¬А);
b) конъюнкция (логическое умножение, логическое И) обозначается /\
(например, А /\ В) либо & (например, А & В);
c) дизъюнкция (логическое сложение, логическое ИЛИ) обозначается \/
(например, А \/ В);
d) следование (импликация) обозначается → (например, А → В);
e) тождество обозначается ≡ (например, A ≡ B). Выражение A ≡ B истинно тогда и только тогда, когда значения A и B совпадают (либо они оба истинны, либо они оба ложны);
f) символ 1 используется для обозначения истины (истинного высказывания); символ 0 – для обозначения лжи (ложного высказывания).
1.2. Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А → В и (¬А) \/ В равносильны, а А /\ В и А \/ В – нет (значения выражений разные, например, при А = 1, В = 0).
1.3. Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), тождество. Таким образом, ¬А \/ В \/ С \/ D означает то же, что и
Возможна запись А \/ В \/ С вместо (А \/ В) \/ С. То же относится и к конъюнкции: возможна запись А /\ В /\ С вместо (А /\ В) /\ С.
2. Свойства
Приведенный ниже список НЕ претендует на полноту, но, надеемся, достаточно представителен.
2.1. Общие свойства
2.2.Дизъюнкция
2.3. Конъюнкция
2.4. Простые дизъюнкции и конъюнкции
Назовем (для удобства) конъюнкцию простой, если подвыражения, к которым применяется конъюнкция, – различные переменные или их отрицания. Аналогично, дизъюнкция называется простой, если подвыражения, к которым применяется дизъюнкция, – различные переменные или их отрицания.
2.5. Импликация