Что означает разложить вектор по базису

Векторное пространство: размерность и базис, разложение вектора по базису

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Исходные данные: векторы

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Исходные данные: векторы

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Ответ: указанная система векторов не является базисом.

Исходные данные: векторы

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Исходные данные: векторы

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Разложение вектора по базису

Таким образом, мы пришли к формулировке важнейшей теоремы:

Докажем эту теорему:

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Вектор x → будет представлен следующим образом:

Запишем это выражение в координатной форме:

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

Решение

Используем метод Гаусса:

Пусть в базисе вектор x → имеет координаты x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

Указанные системы являются также базисами заданного пространства.

n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c

n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c

В виде матрицы систему можно отобразить так:

n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Сделаем по аналогии такую же запись для вектора c ( 2 ) :

n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

И, далее действуя по тому же принципу, получаем:

n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Матричные равенства объединим в одно выражение:

c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c

n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )

Оно и будет определять связь векторов двух различных базисов.

e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e

n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )

Дадим следующие определения:

Источник

Базис векторов и линейные действия над векторами аналитическим путём (теория и решение задач)

Базис – это неопределённое количество векторов в векторном пространстве, и абсолютно любой из этих векторов может создавать линейную комбинацию.

Базис векторов

Так, согласно доказательству (3), произвольные три некомпланарные векторы , , , образуют в трёхмерном пространстве базис, по которому, согласно формуле (2) можно единственным образом разложить произвольный вектор пространства. Векторы , , , которые образуют базис называются базисными.

Будем считать, что базисные векторы , , сведены к точке .

Числ , про которые упоминалось в разделах “линейно зависимая и линейно независимые системы векторов”, называют координатами вектора в заданном базисе, и пишут:

.

Аналогично, на плоскости базис образуют какие-то два неколлинеарные векторы, а любой некомпланарный с ними может быть разложен по этому базису.

Базисным вектором на прямой линии может быть любой ненулевой вектор.\Согласно свойствам линейных операций над векторами, следует, что при сложении и вычитании векторов в данном базисе прибавляются и отнимаются их соответствующие координаты, а при умножении вектора на число умножаются не это число координаты вектора, то есть:

Линейные действия над векторами аналитическим путём

Если раньше линейные действия над векторами осуществлялись графически, то теперь эти операции можно выполнять аналитически, не пользуясь рисунком. Давайте вспомним и сформулируем линейные действия:

Чтобы прибавлять (отнимать) два вектора, необходимо прибавить (отнять) их соответствующие координаты, то есть:

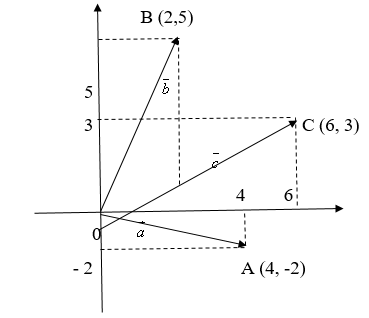
Найти сумму векторов и , заданных на плоскости .

Решение:

Согласно правилу 1 у нас получается:

= (6, 3).

Построим эти векторы: .

Мы видим, что четырёхугольник OABC – параллелограмм. Координаты вектора мы сначала получили путём вычислений (аналитически), без помощи рисунка. Рисунок только подтверждает правило параллелограмма при прибавлении векторов, поэтому дальше рисунками будем пользоваться для наглядности.

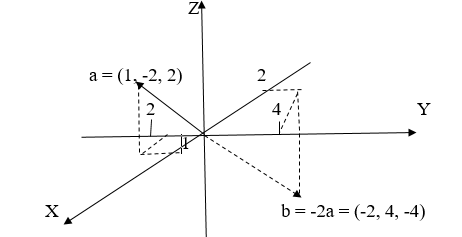
Чтобы умножить вектор на число, необходимо каждую из его координат умножить на это число:

Дан вектор Найти

Решение:

Согласна правилу 2 у нас получается:

Геометрическое изображение смотрите на рис. 4.

Два вектора равны, если у них равны соответствующие координаты:

.

Теперь вы понимаете, как получить координаты вектора не только графическим путём, но и аналитическим. В дальнейшем у вас не возникнет сложностей по этому поводу.

Как найти базис вектора, пример

В некотором базисе заданы своими координатами векторы и Разложить вектор по базису, который образовался из векторов и

Решение:

Разложение вектора по базису и имеет такой вид:

где числа и – неизвестные. Чтобы их найти, подставим в последнее равенство координаты векторов и , а тогда воспользуемся свойствами 1 и 2:

Согласно свойству 3 про равенство векторов, получим систему уравнений:

Первое равенство умножаем на 1, а второе на (- 2) и в итоге у на получается:

.

Значит, ответ у нас выходит:

Источник