Что означает разложить вектор на составляющие по осям x y

Компоненты вектора

Вектор – геометрическое представление величины и направления, выражающиеся стрелками в двух-трех измерениях.

Задача обучения

Основные пункты

Термины

Обзор

Вектор – геометрическое отображение величины и направления, которые чаще всего отмечаются прямыми стрелками, начиная с одной точки на координатной оси и заканчивая на другой. Все векторы наделены длиной, при помощи которого один вектор сравнивают с другим. Векторы со стрелками также обладают направлением. Это главное отличие от скаляров, выступающих простыми числами без направления.

Какие есть составляющие вектора? Вектор характеризуется величиной и позицией относительно оси координат. Полезно анализировать векторы, чтобы разложить на составные части. Если мы говорим о двумерных векторах, то это вертикальные и горизонтальные компоненты. В случае с трехмерными все остается прежним, но теперь мы имеем еще одно направление: x, y, z.

Разложение вектора

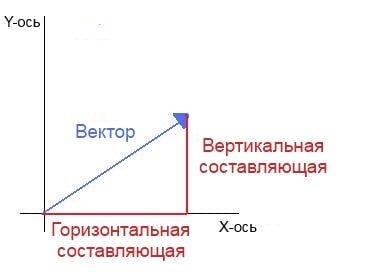
Чтобы визуально разложить вектор на составляющие, начните с системы координат. Далее проведите прямую линию от оси х и продолжайте ее, пока не выровняется с кончиком вектора. Это горизонтальный компонент. Для поиска вертикального, проведите линию от конца горизонтального вектора, пока не дойдете до кончика вектора. В итоге, получите правильный треугольник, в котором вектор играет роль гипотенузы.

Исходный вектор, определенный относительно множества осей. Горизонтальный компонент простирается от начала вектора и до координаты х. Вертикальный тянется от х к самой вертикальной точке. Вместе формируют правильный треугольник

Разделение на горизонталь и вертикаль – удобный способ разобраться в физической проблеме. Как только замечаете движение под углом, вы обязаны воспринимать его как перемещение по горизонтали и вертикали одновременно. Это помогает намного проще отслеживать движение объектов.

Источник

Что означает разложить вектор на составляющие по осям x y

Эти три взаимно перпендикулярных единичных вектора называются ортами.

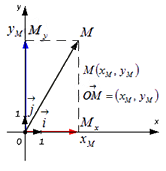
Рассмотрим некоторый вектор а в пространстве. Перенесем его параллельно самому себе так, чтобы его начало совпало с началом координат О.

Другими словами, отложим от начала О вектор ОМ, равный . Проводя через конец вектора ОМ плоскости, параллельные координатным плоскостям, получим параллелепипед, одной из диагоналей которого является вектор ОМ.

Из рис. 69 и из определения суммы нескольких векторов находим:

Так как

Векторы являются составляющими вектора по осям

На основании (49) можем написать:

Обозначая проекции вектора на оси соответственно через из (52) и (53) получаем

Формула (54) дает разложение вектора а на составляющие по координатным осям.

Пусть точка М — конец вектора имеет координаты х, у, z. В таком случае по формуле (46) проекции вектора по осям, очевидно, будут а составляющие по осям — Формула (54) разложения вектора на составляющие примет вид

Если вектор а имеет проекции на оси координат соответственно , то мы будем это записывать следующим образом:

Если известно разложение векторов по осям координат, то линейные операции над векторами можно заменить арифметическими действиями над их проекциями.

Пример. Даны векторы

Найти их сумму и разность.

Решение. Так как при сложении векторов их проекции складываются, а при вычитании вычитаются, то

Зная проекции вектора а, можно легко найти выражение для модуля вектора. Так как вектор является диагональю параллелепипеда, то на основании известной теоремы о длине диагонали прямоугольного параллелепипеда можно написать

но . Поэтому

Модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.

Рассмотрим теперь вектор АВ, начало которого имеет координаты , а конец . По определению проекции вектора на ось находим, что вектор АВ будет иметь следующие проекции:

Поэтому на основании формулы (54) получаем следующее разложение вектора АВ по осям координат:

По формуле (57) находим модуль вектора

Эта формула совпадает с выведенной ранее (гл. I, § 2, п. 5) формулой для расстояния между двумя точками А и В.

Источник

Координаты вектора в декартовой системе координат (ДСК)

Для начала дадим определение координат вектора в заданной системе координат. Чтобы ввести данное понятие, определим что мы называем прямоугольной или декартовой системой координат.

Прямоугольная система координат представляет из себя прямолинейную систему координат с взаимно перпендикулярными осями на плоскости или в пространстве.

С помощью введения прямоугольной системы координат на плоскости или в трехмерном пространстве становится возможным описывание геометрических фигур вместе с их свойствами при помощи уравнений и неравенств, то есть использовать алгебраические методы при решении геометрических задач.

Тем самым, мы можем привязать к заданной системе координат векторы. Это значительно расширит наши возможности при решении определенных задач

Координатные векторы

Векторы i → и j → называются координатными векторами для заданной системы координат.

Разложение вектора

Коэффициенты a x и a y называются координатами вектора в данной системе координат на плоскости.

Следует обратить внимание, что порядок записи координат, имеет важное значение, если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.

Равные и противоположные векторы

Векторы a → и b → равны тогда, когда их соответствующие координаты равны.

Противоположным вектором называется вектор противоположный данному.

Координаты радиус-вектора точки

Чтобы ввести данное определение, требуется показать в данной системе координат связь координат точки и координат вектора.

Вектор O M → называется радиус-вектором точки M .

Определим, какие координаты в данной системе координат имеет радиус-вектор точки

Иначе говоря, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.

Источник

Проекция вектора на ось

Вектор может отбрасывать тень (проекцию) на какую-нибудь ось

Если:

Примечание:

Длина вектора – это положительная величина, а проекция вектора может быть отрицательной

Как разложить вектор на проекции

Мы уже находили длину и направление вектора по его координатам.

Теперь решим обратную задачу: пользуясь длиной и направлением вектора, найдем его координаты.

На плоскости (две оси) легко разложить вектор на проекции, если известны:

Алгоритм действий для разложения вектора на проекции

Важно! Вектор, который мы раскладываем, всегда является гипотенузой.

Формулы разложения вектора на проекции

Формулы разложения легко запомнить с помощью фразы:

Гипотенузу умножаем на косинус (угла), получаем катет, который касается (дуги).

На языке математики эта фраза запишется так:

\[ |\vec| \cdot cos(\alpha) = m_ \]

Катет \( m_ \) – это «x» координата вектора.

Если длину вектора умножим на синус, то получим второй катет:

\[ |\vec| \cdot sin(\alpha) = m_ \]

Катет \( m_ \) – это «y» координата вектора.

Обе формулы запишем в виде системы:

\[ \large \boxed <\begin\left|\vec\right| \cdot cos(\alpha) = m_ \\ \left|\vec\right| \cdot sin(\alpha) = m_ \end> \]

Величина \( |\vec| \) — это длина вектора \( \vec \)

Источник

Что означает разложить вектор на составляющие по осям x y

1. Проекция вектора на заданное направление.

Пусть заданы два вектора `vec a` и `vec b`. Приведём эти векторы к одному началу `O` (рис. 10). Угол, образованный лучами, исходящими из точки `O` и направленными вдоль векторов `vec a` и `vec b`, называют углом между векторами `vec a` и `vec b`. Обозначим этот угол через `alpha`.

Угол `alpha` может принимать различные значения, поэтому в зави­симости от знака `cos alpha` проекция может принимать положительные, отрицательные значения или нуль. Например, если угол `alpha` тупой, т. е. больше, чем `90^@`, но меньше `180^@`, то косинус такого угла отрицателен (см. рис. 11).

Проекция равна нулю, если направления векторов `vec a` и `vec b` взаимно перпендикулярны (см. рис. 12).

Проекции равных векторов на любые направления равны друг другу. Проекции противоположных векторов отличаются знаком.

Легко показать, что проекция суммы векторов равна алгебраической сумме их проекций и что при умножении вектора на число его проекция умножается на то же число.

2. Разложение вектора.

Пусть на плоскости задан вектор `vec a` и две пересекающиеся в точке `O` прямые `AO` и `OB` (см. рис. 13).

Вектор `vec a` можно представить в виде суммы двух векторов, направленных вдоль заданных прямых. Для этого параллельным переносом совместим начало вектора `vec a` с точкой `O` пересечения прямых. Из конца вектора `vec a` проведём два отрезка прямых, параллельных `AO` и `OB`. В результате получится параллелограмм. По построению

В чём разница между проекцией вектора на ось и составляющей (компонентой) вектора вдоль этой оси?

Пусть `a = 1`, угол между прямыми `AO` и `OB` равен `varphi = 45^@`, а угол между векторами `vec a` и `vec(a_1)` равен `varphi = 15^@`. Определите модули векторов `vec a_1` и `vec a_2` в разложении (*), а также значения проекций вектора `vec a` на направления `vec(a_1)` и `vec(a_2)` (см. рис. 13).

`a_(a1) = a cos varphi_1

0,97`, `a_(a2) = a cos varphi_2 = cos 30^@

откуда `a_1 = (sin varphi_2)/(sin (varphi_1 + varphi_2)) = (sin 30^@)/(sin 45^@)

и аналогично `a_2 = (sin 15^@)/(sin 45^@)

3. Проектирование вектора на оси координат.

Особенно важен частный случай разложения вектора по двум взаимно перпендикулярным направлениям. Пусть на плоскости задана прямоугольная система координат `xOy` и некоторый вектор `vec a`. Отложим из начала координат вдоль положительного направления осей `Ox` и `Oy` векторы `vec i` и `vec j` соответственно такие, что `|vec i| = 1` и `|vec j| = 1`. Векторы `vec i` и `vec j` назовём единичными векторами.

Перенесём вектор `vec a` так, чтобы его начало совпало с началом координат. Пусть в этом положении он изображается направленным отрезком `AO` (рис. 14).

Числа `a_x` и `a_y` суть проекции вектора `vec a` на направления векторов `vec i` и `vec j` соответственно, то есть на оси `Ox` и `Oy`. Используется и иная, чем (3), форма записи векторов, а именно `vec a = (a_x ; a_y)`.

Пусть угол между положительным направлением оси `Ox` и вектором `vec a` равен `alpha` (рис.14). Тогда `a_x = a cos alpha`, `a_y = a sin alpha`.

В зависимости от значения угла `alpha` проекции вектора `vec a` на оси прямоугольной системы координат могут быть положительными, отрицательными или равными нулю.

Зная проекции вектора `vec a` на оси координат, можно найти его вели­чину и направление по формулам:

`»tg» alpha = (a_y)/(a_x)` (5)

причём знаки `a_x` и `a_y` будут указывать на то, какому квадранту при­надлежит значение `alpha`.

4. Пусть теперь нам задано векторное равенство `vec a + vec b = vec c` (рис. 15).

Проектируя все векторы на оси координат, получим очевидные равенства

`c_x = a_x + b_x`, `c_y = a_y + b_y`,

`c_x = a cos alpha + b cos beta`,

`c_y = a sin alpha + b sin beta`,

т. е. по проекциям векторов `vec a` и `vec b` легко находятся проекции суммарного вектора `vec c`.

Источник