Что означает свойство полноты и продуктивности модели
Электронная библиотека
Из сказанного ранее следует, что при изучении реально существующего или мыслимого технического объекта математические методы применяют к его математической модели. Это применение будет эффективным, если свойства ММ удовлетворяют определенным требованиям:
Универсальность ММ характеризует полноту отражения в ней свойств реального объекта. Математическая модель отражает не все, а лишь некоторые свойства реального объекта. Например, формулы для сил резания ( ; ; ), не учитывают температуру окружающего воздуха, влажность, экономические параметры и т.д.
Известно, например, что закон Ньютона притяжения двух материальных точек и закон взаимодействия двух точечных электрических зарядов при соответствующем выборе единиц физических величин можно выразить одинаковыми формулами. При помощи одной и той же ММ, содержащей уравнение Пуассона:
где – дифференциальный оператор Лапласа, а u(М) и f(М) – искомая и заданная функции положения точки М в некоторой области V (М V), можно изучать установившиеся процессы течения жидкости и распространения теплоты, распределение электрического потенциала, деформацию мембраны, механические напряжения при кручении бруса, фильтрацию нефти в нефтеносном слое или влаги в почве, распространение какой-либо примеси в воздухе или эпидемии в регионе. В каждой из перечисленных задач функции u(М) и f(М) приобретают свой смысл, но их связь описывает общее для этих задач уравнение.
Приведенные примеры характеризуют свойство универсальности. Благодаря этому свойству возникает «родство» между различными отраслями знаний, что ускоряет их совместное развитие.
Точность ММ дает возможность обеспечить приемлемое совпадение реальных и найденных при помощи ММ значений выходных параметров ТО, составляющих вектор:
Пусть и – найденное при помощи ММ и реальное значения i-го выходного параметра. Тогда относительная погрешность ММ по отношению к этому параметру будет равна:
В качестве скалярной оценки вектора
можно принять какую-либо его норму, например:
Поскольку выходные параметры ТО при помощи ММ связаны с его внешними и внутренними параметрами, то ε, как количественная характеристика точности модели этого ТО, будет зависеть от координат векторов x и g.
Адекватность ММ – это способность ММ отражать характеристики ТО с относительной погрешностью не более некоторого заданного значения δ. Пусть при некоторых ожидаемых номинальных значениях внешних параметров ТО, составляющих вектор хном, из условия минимума ε путем решения задачи
конечномерной оптимизации найдены значения внутренних параметров, составляющие вектор gном и обеспечивающие минимальное значение εmin относительной погрешности ММ. Тогда при фиксированном векторе gном можно построить множество:
называемое областью адекватности данной ММ. Ясно, что X = 0 при δ εmin, тем шире область адекватности ММ, т.е. эта ММ применима в более широком диапазоне возможного изменения внешних параметров ТО.
В более общем смысле под адекватностью ММ понимают правильное качественное и достаточно точное количественное описание именно тех характеристик ТО, которые важны в данном конкретном случае.
Модель, адекватная при выборе одних характеристик, может быть неадекватной при выборе других характеристик того же технического объекта. В ряде прикладных областей, еще недостаточно подготовленных к применению количественных математических методов, ММ имеют главным образом качественный характер. Эта ситуация типична, например, для биологической и социальной сфер, в которых количественные закономерности не всегда поддаются строгой математической формализации. В таких случаях под адекватностью ММ естественно понимать лишь правильное качественное описание поведения изучаемых объектов или их систем.
Экономичность ММ оценивают затратами на вычислительные ресурсы (машинное время и память), необходимые для реализации математической модели на ЭВМ. Эти затраты зависят от числа арифметических операций при использовании модели, от размерности пространства фазовых переменных, от особенностей применяемой ЭВМ и других факторов. Так как указанные величины определяются характеристиками конкретного компьютера, то использовать их для оценки экономичности математической модели не корректно. Поэтому, для оценки экономичности самой математической модели используют другие величины:
· среднее количество операций, выполняемых при одном обращении к математической модели;
· размерность системы уравнений в математической модели;
· количество используемых в модели внутренних параметров и т.д.
Требования высокой степени универсальности, точности, широкой области адекватности математической модели, с одной стороны, и высокой ее экономичности, с
другой стороны, противоречивы. В зависимости от целей и условий эксперимента выбираются конкретные решения.
К математическим моделям предъявляется и целый ряд других требований, среди которых следует выделить следующие:
Полнота ММ позволяет отразить в достаточной мере именно те характеристики и особенности ТО, которые интересуют нас в зависимости от поставленной цели проведения вычислительного эксперимента. Например, модель может достаточно полно описывать протекающие в объекте процессы, но не отражать его габаритные, массовые или стоимостные показатели.
Вычислимость – это возможность ручного или с помощью ЭВМ исследования качественных и количественных закономерностей функционирования объекта (системы).
Модульность – это соответствие конструкций модели структурным составляющим объекта (системы).
Алгоритмизируемость – это возможность разработки соответствующих алгоритма и программы, реализующих математическую модель на ЭВМ.
Робастность (от английского слова robust – крепкий, устойчивый) характеризует ее устойчивость по отношению к погрешностям исходных данных, способность предугадывать эти погрешности и не допускать их чрезмерного влияния на результат вычислительного эксперимента. Причинами низкой робастности математической модели могут быть необходимость при ее количественном анализе вычитания близких друг к другу приближенных значений величин или деления на малую по модулю величину, а также использование в математической модели функций, быстро изменяющихся в промежутке, где значение аргумента известно с невысокой точностью. Иногда стремление увеличить полноту математической модели приводит к снижению
ее робастности вследствие введения дополнительных параметров, известных с невысокой точностью или входящих в слишком приближенные соотношения.
Продуктивность – это возможность располагать достаточно достоверными исходными данными. Если они являются результатом измерений, то точность их измерения должна быть выше, чем для тех параметров, которые получаются при использовании математической модели. В противном случае математическая модель будет непродуктивной, и ее применение для анализа конкретного процесса теряет смысл. Ее можно будет использовать лишь для оценки характеристик некоторого класса процессов с гипотетическими исходными данными.
Наглядность является ее желательным, но необязательным свойством. Тем не менее, использование математической модели и ее модификация упрощаются, если ее составляющие (например, отдельные члены уравнений) имеют ясный содержательный смысл. Это обычно позволяет ориентировочно предвидеть результаты вычислительного эксперимента и облегчает контроль их правильности.
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Что означает свойство полноты и продуктивности модели
3. Понятия содержательной модели, математической модели. Постулаты. Параметры и характеристики моделей. Свойства моделей.
Понятие модели
Множество окружающих нас предметов и явлений обладают различными свойствами. Процесс познания этих свойств состоит в том, что мы создаем для себя некоторое представление об изучаемом объекте, помогающее лучше понять его внутреннее состояние, законы функционирования, основные характеристики. Такое представление, выраженное в той либо иной форме, называется моделью. Как отмечается в [3], под моделью следует понимать любую другую систему, обладающую той же формальной структурой, при условии, что между системными характеристиками модели и оригиналом существует соответствие, и она более проста и доступна для изучения и исследования основных свойств объекта-оригинала.
Любая модель есть объект-заменитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.
С точки зрения философии моделирование следует рассматривать как эффективное средство познания природы. При этом процесс моделирования предполагает наличие объекта исследования, исследователя-экспериментатора и модели.
В автоматизированных системах обработки информации и управления в качестве объекта моделирования могут выступать производственно-технологические процессы получения конечных продуктов; процессы движения документов, информационных потоков при реализации учрежденческой деятельности организации; процессы функционирования комплекса технических средств; процессы организации и функционирования информационного обеспечения АСУ; процессы функционирования программного обеспечения АСУ [2].
Преимущества моделирования состоят в том, что появляется возможность сравнительно простыми средствами изучать свойства системы, изменять ее параметры, вводить целевые и ресурсные характеристики внешней среды.
Как правило, моделирование используется на следующих этапах [2]:
· исследования системы до того, как она спроектирована, с целью определения ее основных характеристик и правил взаимодействия элементов между собой и с внешней средой;
· проектирования системы для анализа и синтеза различных видов структур и выбора наилучшего варианта реализации с учетом сформулированных критериев оптимальности и ограничений;
· эксплуатации системы для получения оптимальных режимов функционирования и прогнозируемых оценок ее развития.
При этом одну и ту же систему можно описать различными типами моделей. Например, транспортную сеть некоторого района можно промоделировать электрической схемой, гидравлической системой, математической моделью с использованием аппарата теории графов.
Для исследования систем широко используются следующие типы моделей: физические (геометрического подобия, электрические, механические и др.) и символические (содержательные и математические).
1. Когнетивная модель.
При наблюдении за объектом в голове у исследователя формируется некий мыслительный образ объекта, его идеализированная модель (Мыслительная модель, способствующая к познанию).
При формировании когнитивной модели исследователи стремятся найти ответы на конкретные вопросы, поэтому от сложного устройства или объекта отсекается все второстепенное с целью оконечного описания.
2. Содержательная модель.
Представление когнетивной модели на естественном языке называется содержательной моделью. Содержательная модель не равна когнетивной, так как не всегда исследователь может выразить в знаковой форме все элементы мысленного образа объекта.
В естественнонаучной дисциплине и в технике содержательную модель называют технической постановкой проблемы.
По функциональному признаку и цели содержательные модели подразделяют на описательные, объяснительные и прогнозирующие.
· Описательные – любое описание объекта.
· Объяснительные – отвечают на вопрос: почему что-либо происходит?
· Прогнозирующие – описывают будущее поведение объекта.
3. Концептуальная модель.
Это содержательная модель, при формулировке которой используется понятие и представление предметных областей знаний занимающихся изучением объекта моделирования.
4. Формальная модель.
Если для описания системы используется естественный язык (язык общения между людьми), то такое описание называется содержательной моделью. Примерами содержательных моделей являются словесные постановки задач, программы и планы развития систем, деревья целей организации и др. Содержательные модели имеют самостоятельную ценность при решении задач исследования и управления системами, а также используются в качестве предварительного шага при разработке математических моделей. Поэтому качество математической модели зависит от качества соответствующей математической модели [9].
В качестве языковых средств описания содержательных моделей используются естественный язык (язык общения между людьми), диаграммы, таблицы, блок-схемы, графы.
Математическая модель
Под математической моделью понимается совокупность математических выражений, описывающих поведение (структуру) системы и те условия (возмущения, ограничения), в которых она работает. В свою очередь, математические модели в зависимости от используемого математического аппарата подразделяются, например:
· на статические и динамические;
· детерминированные и вероятностные;
· дискретные и непрерывные;
· аналитические и численные.
Свойства моделей(из презентации):
n Открытость (модифицируемость)
Свойства модели:
При изучении реально существующей или гипотетической системы математические методы применяют к ее математической модели. Это применение будет эффективным, если свойства ММ удовлетворяют определенным требованиям. Рассмотрим эти свойства.
Полнота ММ позволяет отразить в достаточной мере именно те характеристики и особенности системы, которые интересуют нас с точки зрения поставленной цели проведения вычислительного эксперимента. Например,
модель может достаточно полно описывать протекающие в системе процессы, но не отражать его габаритные, массовые или стоимостные показатели.
Точность ММ дает возможность обеспечить приемлемое совпадение реальных и найденных при помощи ММ значений выходных параметров системы
Адекватность ММ — это способность ММ отражать свойства системы с относительной погрешностью не хуже заданной.
В общем смысле под адекватностью ММ понимают правильное качественное и достаточно точное количественное описание именно тех характеристик системы, которые важны в данном конкретном случае. Модель, адекватная при выборе одних характеристик, может быть неадекватной при выборе других характеристик системы. В ряде прикладных областей, еще недостаточно подготовленных к применению количественных математических методов, ММ имеют главным образом качественный характер. Эта ситуация типична, например, для биологической и социальной сфер, в которых количественные закономерности не всегда поддаются строгой математической формализации. В таких случаях под адекватностью ММ естественно понимать лишь правильное качественное описание поведения изучаемых систем.
Экономичность ММ оценивают затратами на вычислительные ресурсы (машинное время и память), необходимые для реализации ММ на ЭВМ. Эти затраты зависят от числа арифметических операций при использовании модели, от размерности пространства фазовых переменных, от особенностей применяемой ЭВМ и других факторов. Очевидно, что требования экономичности, высокой точности и достаточно широкой области адекватности ММ противоречивы и на практике могут быть удовлетворены лишь на основе разумного компромисса. Свойство экономичности ММ часто связывают с ее простотой. Более того, количественный анализ некоторых упрощенных вариантов ММ может быть осуществлен и без привлечения современной вычислительной техники. Однако его результаты могут иметь лишь ограниченную ценность на стадии отладки алгоритма или программы, если упрощение ММ не согласовано с концептуальной моделью системы.
Робастность ММ характеризует ее устойчивость по отношению к погрешностям исходных данных, способность нивелировать эти погрешности и не допускать их чрезмерного влияния на результат вычислительного эксперимента. Причинами низкой робастности ММ могут быть необходимость при ее количественном анализе вычитания близких друг к другу приближенных значений величин или деления на малую по модулю величину, а также использование в ММ функций, быстро изменяющихся в промежутке, где значение аргумента известно с невысокой точностью.
Продуктивность ММ связана с достоверностью исходных данных. Если они являются результатом измерений, то точность их измерения должна быть выше, чем для тех параметров, которые получаются при использовании ММ. В противном случае ММ будет непродуктивной и ее применение для анализа конкретной системы потеряет смысл. Ее можно будет использовать лишь для оценки и характеристик некоторого класса систем с гипотетическими исходными данными.
Наглядность ММ является желательным, но необязательным свойством. Однако использование ММ и ее модификация упрощаются, если ее составляющие (например, отдельные члены уравнений) имеют ясный содержательный смысл. Это позволяет предвидеть результаты вычислительного эксперимента и облегчить контроль их правильности.
Вариант 2 (свойства)
1. Конечность: модель отображает оригинал лишь в конечном числе его отношений и, кроме того, ресурсы моделирования конечны;
2. Упрощенность: модель отображает только существенные стороны объекта;
3. Приблизительность: действительность отображается моделью грубо или приблизительно;
4. Адекватность: насколько успешно модель описывает моделируемую систему;
6. Потенциальность: предсказуемость модели и её свойств;
7. Сложность: удобство её использования;
8. Полнота: учтены все необходимые свойства;
Параметризация моделей (вариант 2)
Теоретические исследования сложных систем базируются на использовании моделей, отображающих объект исследования в форме, необходимой и достаточной для получения результатов, составляющих цель исследований.
Количественно любая модель, как и соответствующая ей система, описывается совокупностью величин, которые могут быть разбиты на параметры и характеристики. Состав параметров и характеристик модели определяется составом параметров и характеристик исследуемой системы и может в идеальном случае совпадать с ним. В общем случае составы параметров и характеристик модели и системы различаются, т.к. в первом случае они формулируются в терминах того математического аппарата, который используется при построении модели, а параметры и характеристики системы формулируются в терминах соответствующей прикладной области, к которой принадлежит система. В связи с тем, что, в общем случае, параметры и характеристики системы и модели различаются, их принято называть соответственно системными и модельными.
В связи с тем, что состав и номенклатура системных и модельных параметров и характеристик, в общем случае, различается, возникает необходимость установления соответствия между значениями системных и модельных параметров и характеристик, которое выполняется на этапе параметризации модели.
1.1.6. Параметры и характеристики
Количественно любая система описывается совокупностью величин, которые могут быть разбиты на два класса:
· параметры, описывающие первичные свойства системы и являющиеся исходными данными при решении задач анализа;
· характеристики, описывающие вторичные свойства системы и определяемые в процессе решения задач анализа как функция параметров, то есть эти величины являются вторичными по отношению к параметрам.
Множество параметров технических систем можно разделить на:
· внутренние, описывающие структурно-функциональную организацию системы, к которым относятся:
q структурные параметры, описывающие состав и структуру системы;
q функциональные параметры, описывающие функциональную организацию (режим функционирования) системы.
· внешние, описывающие взаимодействие системы с внешней по отношению к ней средой, к которым относятся:
q нагрузочные параметры, описывающие входное воздействие на систему, например частоту и объем используемых ресурсов системы;
q параметры внешней (окружающей) среды, описывающие обычно неуправляемое воздействие внешней среды на систему, например помехи и т.п.
Параметры могут быть:
· детерминированными или случайными;
· управляемыми или неуправляемыми.
Характеристики системы делятся на:
· глобальные, описывающие эффективность системы в целом;
· локальные, описывающие качество функционирования отдельных элементов или частей (подсистем) системы.
К глобальным характеристикам технических систем относятся:
·мощностные (характеристики производительности), описывающие скоростные качества системы, измеряемые, например, количеством задач, выполняемых вычислительной системой за единицу времени;
· временные (характеристики оперативности), описывающие временные аспекты функционирования системы, например время решения задач в вычислительной системе;
· надежностные (характеристики надежности), описывающие надежность функционирования системы;
· экономические (стоимостные) в виде стоимостных показателей, например, стоимость технических и программных средств вычислительной системы, затраты на эксплуатацию системы и т.п.;
· прочие: масса-габаритные, энергопотребления, тепловые и т.п.
Таким образом, параметры системы можно интерпретировать как некоторые входные величины, а характеристики – выходные величины, зависящие от параметров и определяемые в процессе анализа системы
Тогда закон функционирования системы можно представить в следующем виде:
где fс – функция, функционал, логические условия, алгоритм, таблица или словесное описание, определяющее правило (закон) преобразования входных величин (параметров) в выходные величины (характеристики);
H(t) – вектор характеристик, зависящий от текущего момента времени t
Свойства математических моделей
Из сказанного ранее следует, что при изучении реально существующей или гипотетической системы математические методы применяют к ее математической модели. Это применение будет эффективным, если свойства ММ удовлетворяют определенным требованиям. Рассмотрим эти свойства.
Полнота ММ позволяет отразить в достаточной мере именно те характеристики и особенности системы, которые интересуют нас с точки зрения поставленной цели проведения вычислительного эксперимента. Например, модель может достаточно полно описывать протекающие в системе процессы, но не отражать его габаритные, массовые или стоимостные показатели.
Точность ММдает возможность обеспечить приемлемое совпадение реальных и найденных при помощи ММ значений выходных параметров системы, составляющих вектор
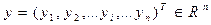
Пусть 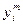
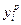
В качестве скалярной оценки вектора
можно принять какую-либо его норму, например
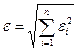
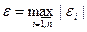
Поскольку выходные параметры системы при помощи ММ связаны с его внешними и внутренними параметрами, то 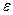
В общем смысле под адекватностью ММ понимают правильное качественное и достаточно точное количественное описание именно тех характеристик системы, которые важны в данном конкретном случае. Модель, адекватная при выборе одних характеристик, может быть неадекватной при выборе других характеристик системы. В ряде прикладных областей, еще недостаточно подготовленных к применению количественных математических методов, ММ имеют главным образом качественный характер. Эта ситуация типична, например, для биологической и социальной сфер, в которых количественные закономерности не всегда поддаются строгой математической формализации. В таких случаях под адекватностью ММ естественно понимать лишь правильное качественное описание поведения изучаемых систем.
Экономичность ММоценивают затратами на вычислительные ресурсы (машинное время и память), необходимые для реализации ММ на ЭВМ. Эти затраты зависят от числа арифметических операций при использовании модели, от размерности пространства фазовых переменных, от особенностей применяемой ЭВМ и других факторов. Очевидно, что требования экономичности, высокой точности и достаточно широкой области адекватности ММ противоречивы и на практике могут быть удовлетворены лишь на основе разумного компромисса. Свойство экономичности ММ часто связывают с ее простотой. Более того, количественный анализ некоторых упрощенных вариантов ММ может быть осуществлен и без привлечения современной вычислительной техники. Однако его результаты могут иметь лишь ограниченную ценность на стадии отладки алгоритма или программы, если упрощение ММ не согласовано с концептуальной моделью системы.
Робастность ММхарактеризует ее устойчивость по отношению к погрешностям исходных данных, способность нивелировать эти погрешности и не допускать их чрезмерного влияния на результат вычислительного эксперимента. Причинами низкой робастности ММ могут быть необходимость при ее количественном анализе вычитания близких друг к другу приближенных значений величин или деления на малую по модулю величину, а также использование в ММ функций, быстро изменяющихся в промежутке, где значение аргумента известно с невысокой точностью.
Продуктивность ММсвязана с достоверностью исходных данных. Если они являются результатом измерений, то точность их измерения должна быть выше, чем для тех параметров, которые получаются при использовании ММ. В противном случае ММ будет непродуктивной и ее применение для анализа конкретной системы потеряет смысл. Ее можно будет использовать лишь для оценки и характеристик некоторого класса систем с гипотетическими исходными данными.
Наглядность ММ является желательным, но необязательным свойством. Однако использование ММ и ее модификация упрощаются, если ее составляющие (например, отдельные члены уравнений) имеют ясный содержательный смысл. Это позволяет предвидеть результаты вычислительного эксперимента и облегчить контроль их правильности.
Дата добавления: 2016-10-18 ; просмотров: 3491 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ