Что означает вынесите общий множитель за скобки
Вынесение общего множителя за скобки
Преобразование математического выражения, в результате которого многочлен представлен произведением нескольких множителей и тождественен (т.е. равен) исходному, называют разложением многочлена на множители.
Чтобы вынести общий множитель за скобки, сначала нужно его найти.
Не забываем полезные лайфхаки для нахождения общего множителя:
Все четные числа делятся на два;
Число делится на три, если сумма составляющих его цифр делится на три
(например, нужно узнать, делится ли на 3 число 78;
7+8=15:3=5, соответственно, 78 делится на 3)
На 5 делятся числа, которые оканчиваются на 0 и 5
Часто в алгебраические выражения и тождества входят буквенные переменные. Например а, в, с, х, у и другие. И многоэтажные примеры в учебники алгебры из нагромождения букв и чисел приводят неподготовленного ученика в священный трепет.
Не стоит пугаться. Буквенная переменная это полноправный множитель, и с ним можно производить все действия, которые применимы к обычным числам: сокращать, выносить за скобки, складывать, возводить в степень и т.д.
Работа с многочленом ведется в определенном порядке.
1.Сначала преобразуем числовые коэффициенты. Определяем, на какое наибольшее целое число (наибольший общий делитель) делятся числовые коэффициенты каждого входящего в уравнение одночлена без остатка.
Определили, что все числовые коэффициенты делятся на 4.
2. Затем находим общие буквенные коэффициенты для всех одночленов многочлена и выносим их за скобки в наименьшей степени.
В нашем примере 8а2+12аb-4a, общим буквенным коэффициентом является а в наименьшей степени 1. Выносим за скобки общий буквенный и определенный на предыдущем этапе общий числовой коэффициенты
NB! Чтобы проверить правильность проведенных преобразований, нужно умножить вынесенный за скобки одночлен на многочлен в скобках. В результате должно получиться исходное выражение.
А сейчас, чтобы закрепить тему «Вынесение за скобки общего множителя», решим пример из учебника «Алгебра» для 7 класса под редакцией Мерзляка А. Г.
Вынесение общего множителя за скобки
Вы будете перенаправлены на Автор24
Сначала давайте вспомним правила умножения одночлена на одночлен:
Для умножения одночлен на одночлен необходимо сначала перемножить коэффициенты одночленов, затем воспользовавшись правилом умножения степеней с одинаковым основанием умножить переменные входящие в состав одночленов.
Решение:
Сначала вычислим проиведение коэффициентов
Получившийся результат оказался неправильной дробью, т. е такой, у которой числитель больше знаменателя.
Преобразуем эту дробь по средствам выделения целой части. Вспомним, что для выделения целой части необходимо неполное частное, получившиеся при делении числителя на знаменатель записать, как целую часть, остаток от деления в числитель дробной части, делитель в знаменатель.
Мы нашли коэффициент будущего произведения.
Тогда итогом умножения одночленов будет:
Тогда исходя из данного правила можно выполнить следующее задание:
Преставим каждый из одночленов,входящих в состав многолена как прозведение двух одночленов для того, чтобы выделить общий одночлен, который будет являться множителем и в первом и во втором одночлене.
Представим первый и второй одночлен, входящий в многочлен как произведение:
$<4x>^3y+8x^2=4x^2\cdot xy + 4x^2\cdot 2$
$<4x>^3y+8х^2 = 4x^2\cdot xy + 4x^2\cdot 2 = 4x^2(xy+2)$
Этот метод называется разложением на множители с помощью вынесения общего множителя.
Готовые работы на аналогичную тему
Алгоритм
Выявить переменные, которые входят в состав каждого одночлена, и выбрать переменную с наименьшим показателем степени
Одночлен, состящий из коэффициента, найденного в п.2, переменных, найденных в п.3 будет общим множителем. который можно вынести за скобки как общий множитель.
Решение:
Найдем НОД коэффициентов для этого разложим коэффициенты на простые множители
И найдем произведение тех, которые входят в разложение каждого:
Выявить переменные, которые входят в состав каждого одночлена, и выбрать переменную с наименьшим показателем степени
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 10 05 2021
Как правильно выносить общий множитель за скобки в алгебре
Понятие вынесения общего множителя за скобки
Разложить многочлен на множители — значит, преобразовать многочлен в произведение, которое равно этому многочлену.
Существует несколько методов в алгебре, позволяющих разложить многочлен на отдельные множители. Одним из наиболее распространенных способов является вынесение общего множителя за скобки. Такая методика часто встречается на уроках в средних классах.
Вынесение общего множителя за скобки представляет собой применение распределительного правила умножения с целью преобразования многочлена и получения в результате произведения.
В процессе вынесения множителя за скобки двучлен (ab + ac) примет вид произведения: a*(b + c)
Как происходит вынесение общего множителя за скобки
Определить общий множитель для каждого из членов, которые входят в состав многочлена, достаточно просто. Нужно следовать следующему алгоритму действий:
В качестве показательного примера можно разобрать порядок разложения многочлена на множители с помощью вынесения общего множителя за скобки:
В первую очередь обратим внимание на коэффициенты 20, 10 и 15 для определения наибольшего общего делителя. Таковым является число 5. Значит, 5 является общим множителем для каждого из коэффициентов.
Далее можно приступить к вычислению многочлена, который остался в скобках. При группировке требуется разделить каждый из членов начального многочлена на определенный ранее общий множитель с учетом его знака:
20 a 2 b c 2 5 a 2 c = 4 b c
10 a 3 c 5 a 2 c = 2 a
15 a 2 b 2 c 5 a 2 c = 3 b 2
В результате проделанной работы получим:
При вынесении общего множителя за скобки совершается действие, которое является обратным умножению одночлена на многочлен:
Основное правило
Основное правило, которое применимо при вынесении общего множителя за скобки: вынесение общего множителя за скобки заключается в записи начального выражения, как произведения общего множителя и скобок, содержащих начальную сумму за исключением общего множителя.
В результате вынесения общего множителя за скобки в них остается такое же количество одночленов, которое содержалось в исходном многочлене.
Например, имеется некое выражение:
Заметим, что это сумма из трех слагаемых и общего множителя в виде числа 4. Руководствуясь правилом вынесения общего множителя за скобки, преобразуем выражение:
Преобразование выполнено, запишем итоговый результат:
Не во всех случаях получается определить общий множитель. Например, перед вынесением общего множителя может потребоваться замена чисел и выражений на произведения, которые тождественно им равны.
Попробуем разложить на множители многочлен:
Пояснение на примерах
В числовом выражении требуется вынести общий множитель за скобки:
В первую очередь следует определить максимально возможный общий множитель для двух слагаемых 15 и 20. Таковым будет являться число 5. Исключим его из скобок:
15 + 20 = 5 ( 15 5 + 20 5 ) = 5 * ( 3 + 4 )
Выполним проверку. В процессе необходимо выполнить умножение общего множителя в виде числа 5 на каждое из слагаемых. В том случае, когда ответ верный, выражение примет вид 15 + 20:
5 * ( 3 + 4 ) = 5 × 3 + 5 × 4 = 15 + 20
Вынести за скобки общий множитель в выражении:
Заметим, что в условии задания записана сумма простых чисел 13 и 5. В связи с этим, такие числа можно разложить на единицу и самих себя:
Такие слагаемые не имеют общих множителей, за исключением единицы. С другой стороны, число 1 бессмысленно выносить за скобки. Выполним преобразования:
13 + 5 = 1 ( 13 1 + 5 1 ) = 1 ( 13 + 5 )
Дано выражение, в котором требуется вынести общий множитель за скобки:
Выполним замену вычитания на сложение:
−20 − 16 − 2 = −20 + (−16) + (−2)
Ответ можно записать в сокращенном виде:
Заметим, что если бы мы вынесли за скобки общий множитель в виде числа 2 без минуса, то получили бы ответ правильный, но не аккуратный:
Дано выражение, в котором требуется вынести за скобки общий множитель:
Выполним замену вычитания на сложение:
Выполним преобразования согласно правилу вынесения общего множителя за скобки:
Что означает вынесите общий множитель за скобки
Цель: совершенствование практических умений и навыков учащихся при разложении многочлена множители путем вынесения общего множителя за скобки.
Тип урока: комбинированный.
1. Организационный момент.
2. Актуализация опорных знаний.
Индивидуальная работа по карточкам №1, №2, №3 (3 учащихся).
Фронтальная работа с классом:
Задание 1. Продолжите фразу:
— Одним из способов разложения многочлена на множители является… (вынесение общего множителя за скобки);
— При вынесении общего множителя за скобки применяется… (распределительное свойство);
— Если все члены многочлена содержат общий множитель, то…(этот множитель можно вынести за скобки)
Какой числовой множитель будет общим в следующих выражениях: 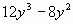
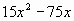
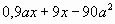
Какую степень множителей 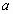
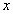
Сформулировать алгоритм вынесения общего множителя.
Укажите общий множитель в данных выражениях: 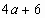
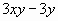
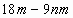
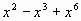
Разложите на множители: 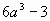
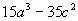
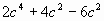
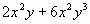
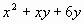
Задание 3. (повторение ранее пройденного)
Вычислите: 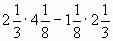
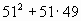
Назовите выражение, противоположное данному 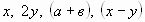
Представьте в виде произведения: 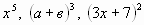
3. Изучение нового материала.
На предыдущем уроке учащиеся уже познакомились с одним из способов разложения многочлена на множители – вынесение общего множителя за скобки. Рассматривался случай, когда за скобки выносили общий множитель, представленный в виде одночлена. Данный урок предполагает совершенствование практических умений и навыков при вынесении общего множителя за скобки, где общий множитель является многочленом.
Пример 1: Разложите на множители многочлен 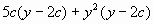
В данном выражении мы видим, присутствует один и тот же множитель 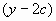
Выражения 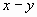
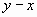
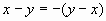
Пример 2: Разложите на множители многочлен
Здесь присутствуют противоположные выражения 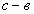
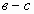
А теперь мы видим, что общий множитель можно вынести за скобки:
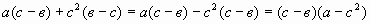
Работа учащихся по заданию карточки № 4 у доски и в тетрадях.
Работа двоих учащихся у доски по заданию карточки №5, остальные выполняют работу самостоятельно по вариантам, затем выполняется проверка и обсуждаются ошибки.
Работа по заданию карточки № 6.
5. Самостоятельная работа.
Учащимся предлагается выполнение самостоятельной работы обучающего характера в виде теста, с последующей самопроверкой (карточка №7), правильные ответы можно расположить на оборотной стороне доски.
6. Подведение итогов урока. Постановка домашнего задания.
Вынесите общий множитель за скобки:
Вынесите общий множитель за скобки:
Вынесите общий множитель за скобки:
Разложите на множители:
Разложите на множители:
Разложите на множители:
Разложите на множители:
Вынесите общий множитель за скобки и выберите верный ответ:
а) 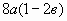
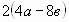

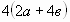
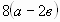
а)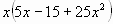

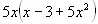
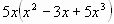
а) 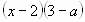
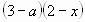
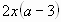
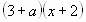
а) 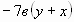
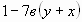
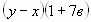
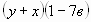
а)
; б)
; в)
; г)
.
Урок изучения нового материала «Вынесение общего множителя за скобки». 7-й класс
Разделы: Математика
Класс: 7
Ход урока:
I. Организационный момент
II. Проверка домашнего задания
Учитель: Давайте вспомним, что мы изучили на прошлом уроке?
Ученики: Умножение одночлена на многочлен.
Учитель: Кто напомнит нам правило умножения одночлена на многочлен?
Ученики: Чтобы умножить одночлен на многочлен, нужно умножить это одночлен на каждый член многочлена и полученные произведения сложить.
Учитель: Тогда проверим, как вы справились с домашним заданием.
<на экране номера с домашним заданием 628 (а), 631 (в, г), 636(а), 643>
III. Актуализация опорных знаний
Учитель: Хорошо, правило вы помните, тогда проверим, как вы устно считаете. Выполнить умножение одночлена на многочлен, т.е. раскрыть скобки:
2х(х 2 + 4ху – 3) = 2х 3 + 8х 2 у – 6х
3(a + b + c) = 3a + 3b + 3c
Учитель: Молодцы, отлично справились, а какое свойство вы использовали?
Ученики: Распределительное свойство умножения относительно сложения и вычитания.
Учитель: Запишем на доске формулу:
А теперь скажите, что получилось в результате умножения одночлена на многочлен в каждом из примеров?
Ученики: Многочлен.
Учитель: То есть, выполнив умножение, мы получили многочлен. Значит, представили произведение в виде многочлена. А сегодня на уроке мы научимся представлять многочлен в виде произведения одночлена и многочлена, то есть раскладывать многочлен на множители. Для этого выполним устно следующее задание. Преобразовать выражение.
23a + 37a = (23 + 37)a = 60a
32a + a = (32 + 1)a = 33a
Учитель: Как вы рассуждали при выполнении этих заданий?
Ученики: Приводили подобные слагаемые, а коэффициенты складывали.
Учитель: почему эти слагаемые или одночлены подобны?
Ученики: Потому что имеют одинаковую буквенную часть «a».
Учитель: Значит, если подробно, то выполняем следующее: <записываю напротив примера>.
Учитель: буква «a» является общим множителем?
Ученики: да.
Учитель: так какое свойство использовали?
Ученики: распределительное свойство умножения, только наоборот.
Учитель: Таким образом, мы представили многочлен в виде произведения с помощью вынесения общего множителя за скобки.
Записываем тему урока: «Вынесение общего множителя за скобки».
IV. Постановка цели урока
Сегодня на уроке мы рассмотрим понятия разложение многочлена на множители и вынесение общего множителя за скобки, сформулируем алгоритм вынесения общего множителя за скобки, научимся применять эти понятия при выполнении упражнений.
V. Объяснение новой темы
Учитель: При решении уравнений, в вычислениях и ряде других задач бывает полезно заменить многочлен произведением нескольких многочленов (среди которых могут быть и одночлены). Представление многочлена в виде произведения двух или более многочленов называют разложением многочлена на множители. Оказывается, что разложение на множители выражения – это операция, обратная почленному умножению одночлена на многочлен. Рассмотрим тот же самый пример, который решали, но в обратном порядке. Разложить на множители – значит вынести за скобки общий множитель.
2х 3 + 8х 2 у – 6х = 2х (х 2 + 4ху – 3).
Я приведу пример вынесения множителя за скобки в русском языке. В выражении “Взять книгу, взять ручку, взять тетрадь” функцию общего множителя выполняет глагол “взять”, а книга, тетрадь и ручка – это дополнения.
Это же выражение можно сказать по-другому “взять книгу, тетрадь и ручку”. Это то же самое, что 3а + 3в + 3с = 3 (а + в + с).
Найти общий множитель (задание на экране)
Рассмотрим многочлен 15x 2 y + 20y 2 x. каждый его член можно представить в виде произведения двух множителей, один из которых равен 5xy:
15x 2 y + 20y 2 x = 5xy3x + 5xy4y.
Полученное выражение на основе распределительного свойства умножения можно представить в виде произведения двух множителей:
Итак: 15x 2 y + 20y 2 x = 5xy(3x + 4y).
Пример 1: Разложите на множители многочлен 5c(y – 2c) + y 2 (y – 2c)
В данном выражении мы видим, присутствует один и тот же множитель (y – 2c), который можно вынести за скобки. Итак, получим: 5c(y – 2c) + y 2 (y – 2c) = (y – 2c)(5c + y 2 ).
Выражения (x–y) и (y–x) являются противоположными, поэтому в некоторых случаях можно пользоваться данным равенством x – y = – (y – x).
Пример 2: Разложите на множители многочлен a(c – b) + c 2 (b – c)
Здесь присутствуют противоположные выражения (c–b) и (b–c), воспользовавшись предыдущим тождеством, мы получим следующую запись:
a(c – b) + c 2 (b – c) = a(c – b) – c 2 (c – b)
А теперь мы видим, что общий множитель можно вынести за скобки:
a(c – b) + c 2 (b – c) = a(c – b) – c 2 (c – b) = (c – b)(a – c 2 ).
VI. Закрепление новой темы
Пример 4. Вынесите общий множитель за скобки: (x + 2y) 2 – 4(x + 2y).
Решение.(x + 2y) 2 – 4(x + 2y) = (x + 2y)(x + 2y – 4).
Общим множителем здесь является двучлен (х + 2у). Мы вынесли его за скобки, а в скобках записали частные от деления данных членов (x + 2y) 2 и – 4(x + 2y) на их общий делитель (х + 2у). В результате мы представили данный многочлен в виде произведения двух многочленов (x + 2y) и (x + 2y – 4), другими словами, мы разложили многочлен (x + 2y) 2 – 4(x + 2y) на множители.
Ответ: (x + 2y)(x + 2y – 4).
Замечание. Иногда мы должны выносить за скобки дробный множитель, это делается из за того, что иногда нам приходится работать с дробями т.к. других чисел просто нету. Например:
2,4x + 7,2y = 2,4(x + 3y)
3a/7 – 6b/7 + 9c/7 = (3/7)(a –2b + 3c).
Сформулируем алгоритм вынесения общего множителя за скобки:
1. Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, он и будет общим числовым множителем;
2. Найти общую буквенную часть для всех членов многочлена (выбрать наименьший показатель степени);
3. Произведение коэффициента и общей буквенной части, найденных на первом и втором шагах, является общим множителем, который выносим за скобки;
4. Делим каждый член многочлена на вынесенный множитель и полученный результат записываем в скобках.
Важно! В скобках должно быть столько одночленов, сколько их было в многочлене.
Преобразовать многочлен (задание на экране).
VII. Самостоятельная работа
1 вариант 2 вариант
1. 6x + 6y = 6(x + y) 1. 8a + 8b = 8(a + b)
2. 3xy – x 2 y 2 = xy(3 – xy) 2. 4xy + x 3 y 3 = xy(4 + x 2 y 2 )
3. 3a – 9ab = 3a(1 + 3b) 3. 36by – 6b = 6b(6y – 1)
4. abc – a 2 b 2 c 2 = abc(1 – abc) 4. x 2 y 2 z 2 + xyz = xyz(xyz + 1)
5. x 2 – x = x(x – 1) 5. a 2 + a = a(a + 1)
6. 3ab – 6b = 3b(a – 2) 6. 7bc –14c = 7c(b – 2)
VIII. Подведение итогов урока
(Систематизация новых знаний с помощью метода незаконченных предложений)
– Cегодня на уроке мы изучали тему… (вынесение общего множителя за скобки);
– Одним из способов разложения многочлена на множители является… (вынесение общего множителя за скобки);
– При вынесении общего множителя за скобки применяется… (распределительное свойство умножения относительно сложения или вычитания);
– Если все члены многочлена содержат общий множитель, то…(этот множитель можно вынести за скобки);
– Мы составили алгоритм… (вынесения общего множителя за скобки)
Важно! После вынесения общего множителя за скобки, в скобках должно остаться столько слагаемых, сколько их было в данном многочлене.
Домашнее задание: П. 28 № 656, 659, 666,670.
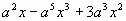
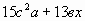
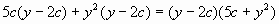
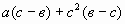
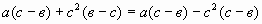
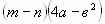 ; б)
; б) 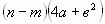 ; в)
; в) 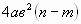 ; г)
; г) 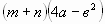 .
.