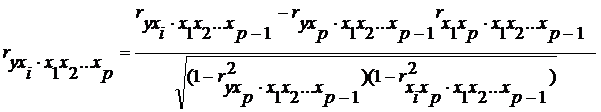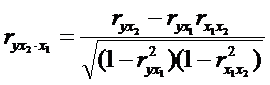Что показывает частный коэффициент корреляции
Частная корреляция. Коэффициенты частной корреляции.



Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в модель.
Частные показатели корреляции широко используются при отборе факторов, когда необходимо оценить целесообразность включения того или иного фактора в уравнение множественной регрессии. Кроме того, они позволяют ранжировать факторы по тесноте их связи с результатом.
Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
В общем виде частный коэффициент корреляции, измеряющий влияние на у фактора хiпри неизменном уровне других факторов, можно определить по формуле:
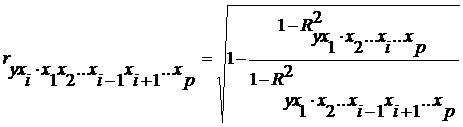
где 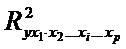
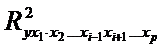
При i=1 формула примет вид:
Коэффициенты частной корреляции могут быть первого, второго, третьего и т.д. порядка. Это зависит от того, влияние скольких факторов элиминируется.
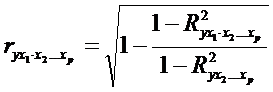
Частная корреляция первого порядка – когда фиксируется теснота связи двух переменных при устранении влияния одного фактора: 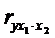
Частная корреляция второго и т.д. порядка – когда фиксируется теснота связи двух переменных при устранении влияния двух и более факторов, например:
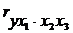
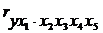
Соответственно, коэффициенты парной корреляции называются коэффициентами нулевого порядка.
Коэффициенты частной корреляции более высоких порядков можно найти через коэффициенты частной корреляции более низких порядков по рекуррентной формуле:
При i=1 и двух факторах формула примет вид:
При i=2 и двух факторах:
Сравнение частных коэффициентов друг с другом позволяет ранжировать факторы по тесноте их связи с результатом. Обычно частные коэффициенты корреляции не имеют самостоятельного значения, они используются на стадии формирования модели, в частности в процедуре отсева факторов.
Контрольные вопросы:
1. В каких ситуациях применяется множественная регрессия?
2. Какие этапы включает в себя построение уравнения множественной регрессии?
3. Какие виды уравнений множественной регрессии различают?
4. Что означает построение модели множественной регрессии в стандартизированном масштабе?
5. Что показывают стандартизированные коэффициенты регрессии?
6. По какой формуле рассчитывается показатель множественной регрессии?
7. Что характеризуют частные коэффициенты корреляции?
Частный коэффициент корреляции и его значения
Вы будете перенаправлены на Автор24
Понятие корреляции
Корреляция – это статистическая зависимость двух и более величин, которые выбираются случайным образом.
В переводе с латинского, корреляция дословно обозначает связь, соотношение. Если в этой зависимости происходит изменение одной из величин, то это ведет к изменению других, связанных с нею величин. Для определения степени взаимосвязи величин используется математический инструмент – коэффициент корреляции. Обычно он обозначается латинской буквой R. Корреляционная связь возникает только тогда, когда осуществляется закономерное изменение другой величины. Если этого не происходит, но имеется изменение какой-либо другой статистической характеристики, то связь между величинами будет называться статистической, но не корреляционной.
Примечательно, что термин «корреляция» был введён палеонтологом, который установил связь между различными органами доисторических животных с целью восстановления их образа. В математике и статистике этот термин стал использоваться в конце 19-го века благодаря Фрэнсису Гальтону.
Корреляционная связь не всегда имеет причинно-следственный характер. Коэффициент устанавливает лишь взаимосвязь со статистической точки зрения. Однако, наличие корреляции может говорить о том, что у двух случайных величин может быть схожая первопричина. Если корреляции между двумя величинами нет, то это не означает полного отсутствия связей между ними. В случае сложной связи, установленной между объектами, корреляция неспособна ее выявить.
Коэффициент корреляции
Готовые работы на аналогичную тему
Чем ближе значение коэффициента к +1, тем прочнее и сильнее связь между двумя исследуемыми величинами. Как правило, коэффициент выражает линейную зависимость двух объектов. Значения коэффициентов могут быть как положительными, так и отрицательными. Положительное значение показывает степень связи, а отрицательное направление этой связи между величинами.
В экономике коэффициент корреляции используется для того, чтобы отслеживать взаимное влияние колебания тех или иных величин. Примером может быть колебание доходности пенсионного фонда в зависимости от текущего индекса цен, применяемого для его расчёта. Чем ближе значение к единице, тем сильнее коррелируют показатели.
Коэффициент корреляции частный, его значения
Частные коэффициенты корреляции используются для отслеживания взаимосвязи изменения величины от множества факторов. Можно сказать, то частный коэффициент показывает степень тесноты связи в случае, когда все остальные признаки исключены из рассматриваемого множества.
Частые коэффициенты могут применяться при отборе факторов воздействия, определении степени их значимости при воздействии на изучаемый объект. Для этих целей строится уравнение репрессии, которое отслеживает факторы по размеру их коэффициента. На каждом шаге исключается частный корреляционный коэффициент с наименьшим значением.
Перед применением частных коэффициентов множество данных тестируется на установление линейных связей. Если связи отсутствуют, то далее осуществляет анализ связи исследуемого объекта и факторов. Частные коэффициенты взаимосвязей позволяют сопоставить взаимное влияние величин и факторов друг на друга для общих отношений и частных соприкосновений.
Значения частного коэффициента корреляции означают следующее:
Частный коэффициент корреляции применяется в эконометрике для того, чтобы отслеживать изменение экономического процесса или явления под воздействием внутренних и внешних факторов.
Частная корреляция
Ранжирование факторов в множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии. Эту цель можно достигнуть с помощью частных коэффициентов корреляции для линейных связей. При нелинейной связи исследуемых признаков эту функцию выполняют частные индексы детерминации. Помимо этого, частные коэффициенты корреляции широко используют при решении проблемы отбора факторов: целесообразность включения фактора в модель может определяться величиной частных коэффициентов корреляции.
Частные коэффициенты корреляции характеризуют тесноту связи между результатом и фактором при устранении влияния другого фактора (или факторов), которые включенны в уравнение регрессии.
Показатели частной корреляции определяются как отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в регрессионную модель.
Частные коэффициенты на основе стандартизованных коэффициентов регрессии (бета-коэффициентов) дают меру тесноты связи каждого фактора с показателем (результатом) в чистом виде. Если из стандартизованного уравнения регрессии следует, что бета 1 > бета 2 > бета 3, т.е. по силе влияния факторов на результат их порядок таков: х1, х2, х3, такой же порядок факторов определяется и по соотношению частных коэффициентов корреляции.
Для уравнения регрессии в стандартизованном виде, коэффициенты могут быть определены по формулам, исходя из решения системы нормальных уравнений:
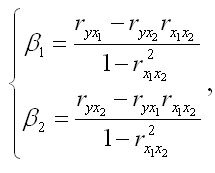

Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.
Частные корреляции. Часть 1
Введение
В данном разделе мы обсуждаем чрезвычайно важное понятие корреляции и частных корреляций. Именно эти понятия лежат в основе статистических выводов, направленных на анализ зависимостей и взаимозависимостей, что является решающим для применения статистических методов на практике.
Действительно, сила статистических методов состоит в том, что они позволяют исследовать зависимость факторов. Материалы этого раздела основаны в основном на книге Кендалла и Стьюарта «Статистические выводы и связи» и снабжены нашими комментариями.
Эти материалы могут показаться техническими, однако они содержат вывод формул, позволяющих непосредственно вычислить частные коэффициенты корреляции, а также позволяют почувствовать саму идею частных корреляций. С помощью STATISTICA Вы можете вычислить частные корреляции двумя щелчками мыши.
Итак, перейдем к систематическому изложению теории частных корреляций.
1. В случае двух нормальных или почти нормальных величин коэффициент корреляции между ними может быть использован в качестве меры взаимозависимости и это подтверждено множеством практических результатов.
Однако при интерпретации «взаимозависимости» часто встречаются следующие трудности: если одна величина коррелирована с другой, то это может быть всего лишь отражением того факта, что они обе коррелированы с некоторой третьей величиной или с совокупностью величин, которые, грубо говоря, остаются за кадром и не введены в модель.
Указанная ситуация приводит к рассмотрению условных корреляций между двумя величинами при фиксированных значениях остальных величин. Это так называемые частные корреляции.
Далее имеют место следующие естественные рассуждения.
Если корреляция между двумя величинами уменьшается, если мы фиксируем некоторую другую случайную величину, то это означает, что их взаимозависимость возникает частично через воздействие этой величины; если же частная корреляция равна нулю или очень мала, то мы делаем вывод, что их взаимозависимость целиком обусловлена собственным воздействием и никак не связана с третьей величиной.
Наоборот, если частная корреляция больше первоначальной корреляции между двумя величинами, то мы заключаем, что другие величины ослабили связь, или, можно сказать, «скрыли» (замазали) корреляцию.
Еще одна тонкость состоит в том, что корреляция не есть причинность. Иными словами, следует помнить, что даже в последнем случае нашего рассуждения мы не имеем права безапелляционно говорить о наличии причинной связи: некоторая совершенно отличная от рассматриваемых в нашем анализе величина может быть источником этой корреляции.
Как при обычной корреляции, так и при частных корреляциях предположение о причинности должно всегда иметь собственные внестатистические основания.
2. В этой области статистики временами трудно достигнуть недвусмысленных и гибких обозначений без того, чтобы они были крайне громоздкими.
Основываясь на системе обозначений Юла (1907), мы будем придерживаться среднего курса, но иногда от читателя потребуется терпение к индексам.
Попутно мы будем рассматривать также линейную регрессию.
Частная корреляция трех величин
3. Вначале естественно рассмотреть три величины, имеющие трехмерное нормальное распределение и в этом простейшем случае выписать формулу для вычисления частных корреляций, т.е. корреляции пары переменных при фиксированном значении третьей.
Исключим вырожденный случай и без потери общности, поскольку мы касаемся лишь корреляций, будем считать величины нормированными.
Тогда их матрица рассеяния совпадает с матрицей их корреляций, которую назовем корреляционной матрицей и обозначим C. Таким образом, если корреляция между xi и xj есть pij, то функция плотности распределения этих трех величин имеет вид



Находим характеристическую функцию (х. ф.) этого распределения

4. Рассмотрим корреляцию между x1 и x2 при фиксированном значении x3. Условное распределение x1 и x2 при заданном x3 равно

где 
Из (4) видно, что при заданном x3 величины x1 и x2 имеют двумерное нормальное распределение с коэффициентом корреляции

Ясно, что p12.3 не зависит от фиксируемого значения величины x3. Кроме того, сокращая на общий множитель |C| из (2) находим

p12.3 называется частным коэффициентом корреляции между x1 и x2 при фиксированном x3. Он симметричен относительно первичных индексов 1, 2. Его вторичный индекс 3 относится к переменной, которая фиксирована.
Хотя (5) выведено в предположении нормальности, мы теперь для любого исходного распределения определим частный коэффициент корреляции с помощью (5). Итак, по определению, для величин, отличных от нормальных, частная корреляция также вычисляется по формуле (5).
Рассмотрим теперь общий случай.
Частная корреляция больше чем трех величин
5. В соответствии с общей концепцией мы рассуждаем следующим образом.
Пусть имеется p-мерное невырожденное нормальное распределение, фиксируем p—2 случайных величины, то получаем частную корреляцию оставшихся двух (скажем, x1 и x2):


Совместная х. ф. всех p величин есть


Если в (8) положить t1=t2=. =tk=0, то из равенства 

Следовательно, после деления (8) на (9) находим

Этот общий результат вытекает из теоремы Барлетта (1938).
Предположим теперь, что наши p величин имеют многомерное нормальное распределение.
Тогда, используя их х. ф., преобразуем подынтегральную функцию числителя в (10):


Учитывая сказанное, из (10) имеем



Если обозначить безусловную (k×k)-матрицу рассеяния <


7. В частности, если зафиксировать только одну переменную, скажем xp, то Dpp=1, и условная ковариация (14) тогда равна

При u=v из (15) находим условную дисперсию u:

Из двух последних формул получаем условный коэффициент корреляции того же вида, что и (5):

Если зафиксируем все переменные, кроме двух, скажем x1 и x2, то из (14) будем иметь

Рассматривая (7), находим, что минор элемента p12, а именно

может быть разложен по его первой строке и столбцу в виде

и аналогично для миноров элементов p11, p22. Таким образом, (16) представимо в форме

Множественная корреляция, её коэффициент. Частная корреляция
Множественная корреляция, её коэффициент
Для того чтобы можно было бы применять модель множественной линейной регрессии, прежде, при анализе множественной корреляции должны быть установлены следующие факты:
Коэффициент множественной корреляции в случае двухфакторной корреляции рассчитывается по следующей формуле:

| Y | X 1 | X 2 | X 3 | X 4 | |
| Y | 1 | ||||
| X 1 | -0,27 | 1 | |||
| X 2 | 0,78 | -0,63 | 1 | ||
| X 3 | -0,83 | 0,47 | -0,89 | 1 | |
| X 4 | 0,65 | -0,46 | 0,17 | -0,21 | 1 |
Установить, какие переменные можно выбрать как независимые, для того, чтобы далее можно было бы строить модель множественной регрессии.
Корреляционная матрица показывает, что между переменными:
Таким образом, между заработной платой сотрудников, с одной стороны, и оценкой теста для приёма на работу и числом подчинённых, с другой стороны, существует тесная линейная связь.
Как показывает пример выше, в исследованиях поведения человека, как и во многих других направлениях, важно установить, какие факторы из многих действительно влияют на результат при учете влияния всех остальных факторов.
Частная корреляция
С помощью коэффициента частной корреляции определяется теснота связи между двумя факторами при фиксировании или исключении влияния остальных. Коэффициент частной корреляции рассчитывается по следующей формуле:
Пример 2. Собраны данные для установления зависимости цены квартиры, с одной стороны, и общей площади, площади жилой зоны и площади кухни, с другой стороны. Установить тесноту связи между ценой квартиры и её общей площади при исключении влияния площади жилой зоны и площади кухни.