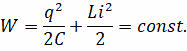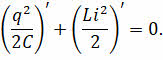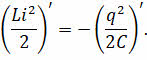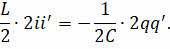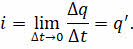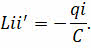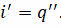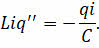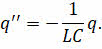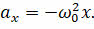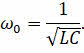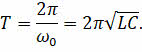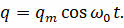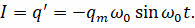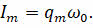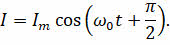Что показывает формула томсона

§ 2.3. Формула Томсона

Формула Томсона

Наша задача в первую очередь будет заключаться в определении периода (или частоты) свободных электрических колебаний. Правда, основываясь на аналогии между свободными механическими и свободными электрическими колебаниями, можно сразу записать выражения для частоты и периода свободных электрических колебаний.

Действительно, так как в формуле для циклической частоты свободных колебаний шарика на пружине — величина k аналогична , а m — индуктивности L, то частота свободных электрических колебаний должна быть равна:

Для периода свободных колебаний можно записать:

Формула (2.3.2) называется формулой Томсона в честь английского физика, который ее впервые вывел.

Полученные нами результаты правильны. Однако все же считать их достаточно строго доказанными нельзя. Необходимо показать, что уравнение, описывающее электрические колебания в контуре, в математическом отношении не отличается от уравнения, описывающего свободные механические колебания. Лишь после этого мы с полной уверенностью сможем утверждать, что механические и электрические колебания управляются одними и теми же количественными законами. А это и есть самое важное.

Уравнение, описывающее процессы в колебательном контуре

Основное уравнение для процессов в колебательном контуре можно записать, используя закон Ома в дифференциальной форме:

Здесь i — плотность тока, γ — удельная проводимость, — напряженность потенциального электрического поля в проводнике, созданного поверхностными зарядами, _ст — напряженность поля сторонних сил. В случае колебательного контура без источников тока _ст — это напряженность вихревого (непотенциального) поля.

Рассмотрим колебательный контур, содержащий все три основных элемента: конденсатор емкостью С, катушку индуктивностью L и резистор сопротивлением R (рис. 2.7).

Сопротивлением катушки, пластин конденсатора и соединительных проводов пренебрежем. Весь контур между точками 1 и 2 разобьем на малые элементы . Положительное направление обхода контура выберем по часовой стрелке. Запишем уравнение (2.3.3) для каждого элемента и умножением обеих частей на приведем его к виду:

Теперь просуммируем уравнения (2.3.4), записанные для всех элементов . контура между точками 1 и 2:

Выясним физический смысл каждого из членов уравнения (2.3.5). Рассмотрим сумму в левой части уравнения. Для всей цепи, кроме резистора, удельная проводимость бесконечна, так как мы сопротивление этой части цепи полагаем пренебрежимо малым. Далее, будем считать резистор состоящим из тонкой проволоки постоянного поперечного сечения площадью S и постоянной удельной проводимости γ. Тогда плотность тока _i будет направлена по и приблизительно постоянна по сечению. Поэтому можно принять, что

где i — сила тока в цепи.

При этих предположениях

где i длина проволоки резистора.

есть не что иное, как сопротивление резистора.

Рассмотрим первый член правой части уравнения (2.3.5). Он численно равен работе кулоновского поля, созданного поверхностными зарядами проводника, при перемещении единичного заряда вдоль контура от точки 1 к точке 2, т. е. разности потенциалов (или напряжению) на конденсаторе:

где q — заряд правой пластины конденсатора.

Второй член правой части уравнения (2,3.5) численно равен работе сторонних сил (вихревого электрического поля) в контуре по перемещению единичного заряда, т. е. представляет собой ЭДС самоиндукции. Согласно закону электромагнитной индукции:

Теперь силу тока выразим через производную заряда конденсатора. Здесь имеется небольшая тонкость. При выбранном направлении обхода контура сила тока, направленного от правой пластины конденсатора, положительна. Эта пластина разряжается и ее заряд уменьшается. Изменение заряда Δq за малый интервал времени Δt отрицательно. Для того чтобы сила тока была положительной величиной, ее надо определить так:

Если бы вместо заряда q правой пластины мы взяли заряд левой пластины, то i = +q’. В напхем случае справедливо равенство (2.3.10). Окончательно уравнение (2.3.5) запишем в форме:

Это и есть основное уравнение для процессов в колебательном контуре. Оно аналогично уравнению (1.9.5) с правой частью, равной нулю. (Такое уравнение будет описывать свободные затухающие колебания.)

Строгий вывод формулы Томсона

Теперь, наконец, вы в полной мере сможете оценить те усилия, которые были затрачены для изучения колебаний груза на пружине и математического маятника. Ведь уравнение (2.3.12) ничем, кроме обозначений, не отличается от уравнения (1.2.4), описывающего колебания груза на пружине. При замене m ⇒ L, а_x = х» ⇒ q», k ⇒ и x ⇒ q мы в точности получим уравнение (2.3.12) вместо (1.2.4).

Но уравнение (1.2.4) или эквивалентное ему уравнение (1.4.1) нами уже решено. Поэтому, зная, как колеблется груз, мы сразу можем сказать, как происходят колебания в контуре.

Разделив правую и левую части уравнения (2.3.12) на L и введя обозначение

А это то же самое, что и уравнение (1.4.1). В уравнении (1.4.1) ω₀ — циклическая частота колебаний. Значит, и величина ω₀, определяемая выражением (2.3.13), тоже является частотой колебаний, но теперь уже частотой электрических колебаний (заряда, силы тока и других величин). Период свободных колебаний в контуре равен:

Это и есть формула Томсона.

Конечно, и без каких-либо уравнений мы могли бы сообразить, что период Т должен увеличиваться с ростом индуктивности L и емкости С. Действительно, при увеличении L сила тока медленнее нарастает со временем и медленнее падает до нуля. А чем больше емкость, тем большее время требуется для перезарядки конденсатора. Но получить формулу (2.3.15) строго без уравнения (2.3.14) мы бы не смогли.

Гармонические колебания заряда и силы тока

Подобно тому, как координата при механических колебаниях меняется по гармоническому закону, точно также заряд конденсатора меняется по закону синуса или косинуса:

Здесь q_m — амплитуда колебаний заряда, а φ₀ — начальная фаза колебаний. Эти величины определяются начальными условиями, т. е. значениями заряда и силы тока в начальный момент времени: q(0) = q₀ и i(0) = i₀.

Если в начальный момент времени q(0) = q₀, а i(0) = i₀, то колебания совершаются по косинусоидальному закону с нулевой начальной фазой* и амплитудой q_m = q₀:

Точно так же изменяется координата груза на пружине, если вы вывели груз из положения равновесия и не сообщили ему начальной скорости.

Сила тока также совершает гармонические колебания. Если q = q₀ cos (ω₀t + φ₀), то

где I_m = ωq_m — амплитуда колебаний силы тока. Колебания силы тока смещены по фазе относительно колебаний заряда на . При начальных условиях q(0) = q₀, i(0) = 0

Колебания заряда и силы тока для этого случая графически представлены на рисунке 2.8.

В действительности из-за энергетических потерь колебания будут затухающими. Чем больше сопротивление R, тем больше будет период колебаний. При достаточно большом сопротивлении колебания не возникают. Конденсатор разрядится, но перезарядки не произойдет.

* Именно такой случай описан в § 2.2, когда колебания в контуре начинались после замыкания цепи предварительно заряженного конденсатора.

Источник

Идеальный колебательный контур. Формула Томсона

Урок 11. Физика 11 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Идеальный колебательный контур. Формула Томсона»

На прошлом уроке мы с вами познакомились с электромагнитными колебаниями. Напомним, что так называют периодические изменения со временем электрических и магнитных величин в электрической цепи.

Рассмотрев качественную сторону теории процессов в колебательном контуре, перейдём к её количественной стороне. Для этого рассмотрим идеальный колебательный контур, то есть контур, активное сопротивление которого пренебрежимо мало.

В таком контуре, как мы показали ранее, полная электромагнитная энергия в любой момент времени равна сумме энергий электрического и магнитного полей, и она не меняется с течением времени:

А раз энергия контура неизменная, то производная полной энергии по времени равна нулю:

Напомним, что в записанной формуле заряд и сила тока в цепи являются функцией времени.

Чтобы понять физический смысл этого уравнения, перепишем его так:

Из такой записи видно, что скорость изменения магнитного поля по модулю равна скорости изменения энергии электрического поля. А знак минус в формуле показывает на то, что увеличение энергии магнитного поля происходит за счёт убыли энергии поля электрического.

Вычислим производные в записанном уравнении, воспользовавшись для этого формулой вычисления производной сложной функции.

А теперь вспомним, что производная заряда по времени есть сила мгновенного тока (то есть сила тока в данный момент времени):

Поэтому предыдущее уравнение можно переписать так, как показано на экране:

Производная силы тока по времени есть не что иное, как вторая производная заряда по времени, подобно тому, как производная скорости по времени (то есть ускорение) есть вторая производная координаты по времени:

Перепишем предыдущее равенство с учётом этой поправки:

Разделив левую и правую части этого уравнения на «Эль И» (Li), получим основное уравнение, описывающее свободные гармонические электрические колебания в контуре:

Данное уравнение аналогично уравнению, описывающему гармонические механические колебания:

Отсюда видно, что величина, обратная квадратному корню из произведения индуктивности и ёмкости, является циклической частотой свободных электрических колебаний:

Зная циклическую частоту колебаний, нетрудно найти и их период, то есть минимальный промежуток времени, через который процесс в колебательном контуре полностью повторяется:

Эта формула впервые была получена английским физиком Уильямом Томсоном 1853 году, и в настоящее время носит его имя.

Из формулы видно, что период колебательного контура определяется параметрами составляющих его элементов: индуктивностью катушки и ёмкостью конденсатора. Из формулы Томсона также следует, что, например, при уменьшении ёмкости или индуктивности период колебаний должен уменьшиться, а их частота — увеличиться и наоборот.

Но вернёмся к уравнению свободных электромагнитных колебаний в идеальном колебательном контуре. Его решением является уравнение, выражающее зависимость заряда конденсатора от времени:

В записанной формуле q_m — это начальное (или амплитудное) значение заряда, сообщённому конденсатору. Из этой формулы следует, что заряд на конденсаторе изменяется со временем по гармоническому закону.

Если взять первую производную заряда конденсатора по времени, то мы получим уравнение, описывающее изменение силы тока в контуре:

Величина, равная произведению максимального заряда конденсатора и циклической частоты колебаний, является амплитудным значением силы тока:

Перепишем уравнение для силы тока с учётом последнего равенства, а также воспользовавшись формулой приведения:

Из такой записи хорошо видно, что сила тока в колебательном контуре также совершает гармонические колебания с той же частотой, но по фазе она смещена на π/2 относительно колебаний заряда.

Для закрепления материала, решим с вами такую задачу. Конденсатор ёмкостью 2 мкФ зарядили до напряжения 100 В, а затем замкнули на катушку с индуктивностью 5 мГн. Определите заряд конденсатора через 0,025π мс после замыкания.

В заключение отметим, что в реальных колебательных контурах всегда имеется активное сопротивление, поэтому часть энергии контура всегда превращается во внутреннюю проводников, которая выделяется в виде излучения. Кроме того, часть энергии теряется на перемагничивание сердечника и изменение поляризации диэлектрика. Поэтому полная энергия контура с течением времени уменьшается, в результате уменьшается и амплитуда колебаний. Следовательно, реальные электромагнитные колебания в контуре являются затухающими.

Источник

ТОМСОНА ФОРМУЛА

Смотреть что такое «ТОМСОНА ФОРМУЛА» в других словарях:

Формула Томсона — Колебательный контур Формула Томсона названа в честь английского физика Уильяма Томсона, который вывел её в 1853 году, и связывает период собственных электрическ … Википедия

формула Томсона — Tomsono virpesių formulė statusas T sritis fizika atitikmenys: angl. Thomson’s formula vok. Thomsonsche Schwingungsformel, f rus. формула Томсона, f pranc. formule de Thomson, f … Fizikos terminų žodynas

Формула Клейна — Зависимость дифференциального сечения рассеяния от угла рассеяния для различных значений энергий фотона Формула Клейна Нишины формула, описывающая … Википедия

Эффект Томсона — Эффект Томсона одно из термоэлектрических явлений, заключающееся в том, что в однородном неравномерно нагретом проводнике с постоянным током, дополнительно к теплоте, выделяемой в соответствии с законом Джоуля Ленца, в объёме… … Википедия

Электрохимия* — Содержание: Введение. Историческая справка. Обозначения, принятые в Э. Основные законы и принципы. Перенос ионов. Электропроводность растворов. Электровозбудительная сила. Переход химической энергии в электрическую. Классификация гальванических… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Электрохимия — Содержание: Введение. Историческая справка. Обозначения, принятые в Э. Основные законы и принципы. Перенос ионов. Электропроводность растворов. Электровозбудительная сила. Переход химической энергии в электрическую. Классификация гальванических… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Кинетическая теория газов — Сущность ее может быть выражена в немногих словах. Согласно этой теории, газы состоят из огромного числа отдельных весьма малых частиц, двигающихся по всем возможным направлениям и со всеми возможными скоростями; частицы эти связаны между собой… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Эквивалентность массы и энергии — Эта статья включает описание термина «E=mc2»; см. также другие значения. Формула на небоскрёбе Тайбэй 101 во время одного из мероприятий Всемирного года физики (2005) Экв … Википедия

Важнейшие открытия в физике — История технологий По периодам и регионам: Неолитическая революция Древние технологии Египта Наука и технологии древней Индии Наука и технологии древнего Китая Технологии Древней Греции Технологии Древнего Рима Технологии исламского мира… … Википедия

Источник

§ 2.3. Формула Томсона

Формула Томсона

Наша задача в первую очередь будет заключаться в определении периода (или частоты) свободных электрических колебаний. Правда, основываясь на аналогии между свободными механическими и свободными электрическими колебаниями, можно сразу записать выражения для частоты и периода свободных электрических колебаний. Действительно, так как в формуле для циклической частоты свободных колебаний шарика на пружине — величина k аналогична , а m — индуктивности L, то частота свободных электрических колебаний должна быть равна:

Для периода свободных колебаний можно записать:

Формула (2.3.2) называется формулой Томсона в честь английского физика, который ее впервые вывел.

Полученные нами результаты правильны. Однако все же считать их достаточно строго доказанными нельзя. Необходимо показать, что уравнение, описывающее электрические колебания в контуре, в математическом отношении не отличается от уравнения, описывающего свободные механические колебания. Лишь после этого мы с полной уверенностью сможем утверждать, что механические и электрические колебания управляются одними и теми же количественными законами. А это и есть самое важное.

Уравнение, описывающее процессы в колебательном контуре

Основное уравнение для процессов в колебательном контуре можно записать, используя закон Ома в дифференциальной форме:

Здесь i — плотность тока, γ — удельная проводимость, — напряженность потенциального электрического поля в проводнике, созданного поверхностными зарядами, _ст — напряженность поля сторонних сил. В случае колебательного контура без источников тока _ст — это напряженность вихревого (непотенциального) поля.

Рассмотрим колебательный контур, содержащий все три основных элемента: конденсатор емкостью С, катушку индуктивностью L и резистор сопротивлением R (рис. 2.7).

Сопротивлением катушки, пластин конденсатора и соединительных проводов пренебрежем. Весь контур между точками 1 и 2 разобьем на малые элементы . Положительное направление обхода контура выберем по часовой стрелке. Запишем уравнение (2.3.3) для каждого элемента и умножением обеих частей на приведем его к виду:

Теперь просуммируем уравнения (2.3.4), записанные для всех элементов . контура между точками 1 и 2:

Выясним физический смысл каждого из членов уравнения (2.3.5). Рассмотрим сумму в левой части уравнения. Для всей цепи, кроме резистора, удельная проводимость бесконечна, так как мы сопротивление этой части цепи полагаем пренебрежимо малым. Далее, будем считать резистор состоящим из тонкой проволоки постоянного поперечного сечения площадью S и постоянной удельной проводимости γ. Тогда плотность тока _i будет направлена по и приблизительно постоянна по сечению. Поэтому можно принять, что

где i — сила тока в цепи.

При этих предположениях

где i длина проволоки резистора.

есть не что иное, как сопротивление резистора.

Рассмотрим первый член правой части уравнения (2.3.5). Он численно равен работе кулоновского поля, созданного поверхностными зарядами проводника, при перемещении единичного заряда вдоль контура от точки 1 к точке 2, т. е. разности потенциалов (или напряжению) на конденсаторе:

где q — заряд правой пластины конденсатора.

Второй член правой части уравнения (2,3.5) численно равен работе сторонних сил (вихревого электрического поля) в контуре по перемещению единичного заряда, т. е. представляет собой ЭДС самоиндукции. Согласно закону электромагнитной индукции:

Теперь силу тока выразим через производную заряда конденсатора. Здесь имеется небольшая тонкость. При выбранном направлении обхода контура сила тока, направленного от правой пластины конденсатора, положительна. Эта пластина разряжается и ее заряд уменьшается. Изменение заряда Δq за малый интервал времени Δt отрицательно. Для того чтобы сила тока была положительной величиной, ее надо определить так:

Если бы вместо заряда q правой пластины мы взяли заряд левой пластины, то i = +q’. В напхем случае справедливо равенство (2.3.10). Окончательно уравнение (2.3.5) запишем в форме:

Это и есть основное уравнение для процессов в колебательном контуре. Оно аналогично уравнению (1.9.5) с правой частью, равной нулю. (Такое уравнение будет описывать свободные затухающие колебания.)

Строгий вывод формулы Томсона

Теперь, наконец, вы в полной мере сможете оценить те усилия, которые были затрачены для изучения колебаний груза на пружине и математического маятника. Ведь уравнение (2.3.12) ничем, кроме обозначений, не отличается от уравнения (1.2.4), описывающего колебания груза на пружине. При замене m ⇒ L, а_x = х» ⇒ q», k ⇒ и x ⇒ q мы в точности получим уравнение (2.3.12) вместо (1.2.4).

Но уравнение (1.2.4) или эквивалентное ему уравнение (1.4.1) нами уже решено. Поэтому, зная, как колеблется груз, мы сразу можем сказать, как происходят колебания в контуре.

Разделив правую и левую части уравнения (2.3.12) на L и введя обозначение

А это то же самое, что и уравнение (1.4.1). В уравнении (1.4.1) ω₀ — циклическая частота колебаний. Значит, и величина ω₀, определяемая выражением (2.3.13), тоже является частотой колебаний, но теперь уже частотой электрических колебаний (заряда, силы тока и других величин). Период свободных колебаний в контуре равен:

Это и есть формула Томсона.

Конечно, и без каких-либо уравнений мы могли бы сообразить, что период Т должен увеличиваться с ростом индуктивности L и емкости С. Действительно, при увеличении L сила тока медленнее нарастает со временем и медленнее падает до нуля. А чем больше емкость, тем большее время требуется для перезарядки конденсатора. Но получить формулу (2.3.15) строго без уравнения (2.3.14) мы бы не смогли.

Гармонические колебания заряда и силы тока

Подобно тому, как координата при механических колебаниях меняется по гармоническому закону, точно также заряд конденсатора меняется по закону синуса или косинуса:

Здесь q_m — амплитуда колебаний заряда, а φ₀ — начальная фаза колебаний. Эти величины определяются начальными условиями, т. е. значениями заряда и силы тока в начальный момент времени: q(0) = q₀ и i(0) = i₀.

Если в начальный момент времени q(0) = q₀, а i(0) = i₀, то колебания совершаются по косинусоидальному закону с нулевой начальной фазой* и амплитудой q_m = q₀:

Точно так же изменяется координата груза на пружине, если вы вывели груз из положения равновесия и не сообщили ему начальной скорости.

Сила тока также совершает гармонические колебания. Если q = q₀ cos (ω₀t + φ₀), то

где I_m = ωq_m — амплитуда колебаний силы тока. Колебания силы тока смещены по фазе относительно колебаний заряда на . При начальных условиях q(0) = q₀, i(0) = 0

Колебания заряда и силы тока для этого случая графически представлены на рисунке 2.8.

В действительности из-за энергетических потерь колебания будут затухающими. Чем больше сопротивление R, тем больше будет период колебаний. При достаточно большом сопротивлении колебания не возникают. Конденсатор разрядится, но перезарядки не произойдет.

* Именно такой случай описан в § 2.2, когда колебания в контуре начинались после замыкания цепи предварительно заряженного конденсатора.

Источник