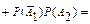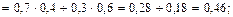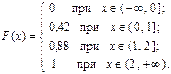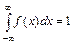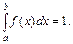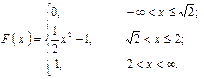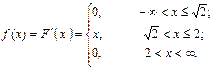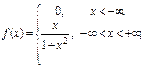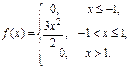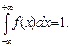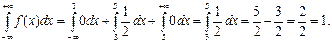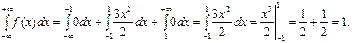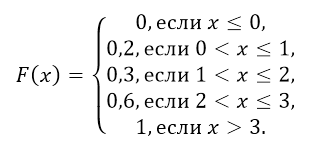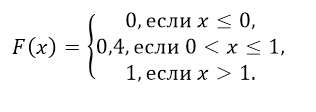Что показывает функция распределения случайной величины
Функции случайных величин
Закон распределения вероятностей функции одной случайной величины
При решении задач, связанных с оценкой точности работы различных автоматических систем, точности производства отдельных элементов систем и др., часто приходится рассматривать функции одной или нескольких случайных величин. Такие функции также являются случайными величинами. Поэтому при решении задач необходимо знать законы распределения фигурирующих в задаче случайных величин. При этом обычно известны закон распределения системы случайных аргументов и функциональная зависимость.
Таким образом, возникает задача, которую можно сформулировать так.
Рассмотрим задачу о законе распределения функции одного случайного аргумента
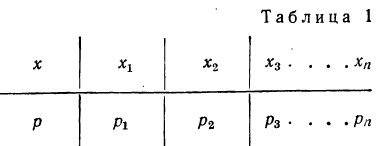
Пусть — дискретная случайная величина, имеющая ряд распределения
и искомый ряд распределения имеет вид
Если же среди чисел есть одинаковые, то каждой группе одинаковых значений нужно отвести в таблице один столбец и соответствующие вероятности сложить.
Пример 1. Случайная величина распределена с плотностью
Решение. Обратная функция неоднозначна. Одному значению аргумента соответствуют два значения функции
Закон распределения функции двух случайных величин
Будем полагать, что эта система однозначно разрешима относительно
и удовлетворяет условиям дифференцируемости.
Плотность распределения случайной величины
Математическое ожидание функции случайных величин
На практике часто встречаются случаи, когда нет особой надобности полностью определять закон распределения функции случайных величин, а достаточно только указать его числовые характеристики. Таким образом, возникает задача определения числовых характеристик функций случайных величин помимо законов распределения этих функций.
Пусть случайная величина является функцией случайного аргумента с заданным законом распределения
Пусть — дискретная случайная величина, имеющая ряд распределения
Составим таблицу значений величины и вероятностей этих значений:
так как величина, определяемая формулой (6.4), не может измениться от того, что под знаком суммы некоторые члены будут заранее объединены, а порядок членов изменен.
Для непрерывной случайной величины математическое ожидание вычисляется по формуле
Рассмотрим случаи, когда для нахождения математического ожидания функции случайных аргументов не требуется знание даже законов распределения аргументов, а достаточно знать только некоторые их числовые характеристики. Сформулируем эти случаи в виде теорем.
Теорема 6.1. Математическое ожидание суммы как зависимых, так и независимых двух случайных величин равно сумме математических ожиданий этих величин:
Теорема 6.2. Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:
Следствие 6.1. Математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий.
Следствие 6.2. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
Дисперсия функции случайных величин
Приведем расчетные формулы только для случая непрерывных случайных аргументов. Для функции одного случайного аргумента дисперсия выражается формулой
Формулу (6.5) можно заменить на следующую:
Теорема 6.3. Дисперсия суммы случайных величин равна сумме дисперсий этих величин плюс удвоенная сумма корреляционных моментов каждой из слагаемых величин со всеми последующими:
Следствие 6.3. Дисперсия суммы некоррелированных случайных величин равна сумме дисперсий слагаемых:
Теорема 6.4. Дисперсия произведения двух независимых случайных величин вычисляется по формуле
Корреляционный момент функций случайных величин
Раскрывая скобки и применяя свойства математического ожидания, получаем
Рассмотрим две функции случайной величины
Согласно формуле (6.6)
т.е. корреляционный момент двух функций случайных величин равен математическому ожиданию произведения этих функций минус произведение из математических ожиданий.
Свойство 1. От прибавления к случайным величинам постоянных величин корреляционный момент и коэффициент корреляции не изменяются.
Свойство 2. Для любых случайных величин и абсолютная величина корреляционного момента не превосходит среднего геометрического дисперсий данных величин:
Следствие 6.5. Для любых случайных величин и абсолютная величина коэффициента корреляции не превосходит единицы:
Функция распределения



Универсальным способом задания закона распределения, пригодным как для дискретных, так и для непрерывных случайных величин, является функция распределения.
Функцией распределения случайной величины X называется функция F(x), определяющая для каждого значения x вероятность того, что случайная величина X примет значение меньшее, чем x, то есть
Функция распределения дискретных случайных величин может быть определена по формуле
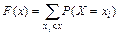
Если известен ряд распределения дискретной случайной величины, легко вычислить и построить ее функцию распределения. Продемонстрируем, как это делается на примере 23.
Пример 25. Вычислить и построить функцию распределения для дискретной случайной величины, закон распределения которой, имеет вид:
| xi | 0,1 | 1,2 | 2,3 | 4,5 |
| pi | 0,1 | 0,2 | 0,6 | 0,1 |
Решение. Определим значения функции F(x) = P(X
Из непрерывности функции F(x) следует, что вероятность каждого отдельного значения непрерывной случайной величины равна нулю.
Так как вероятность каждого отдельного значения непрерывной случайной величины равна 0, свойство 3 функции распределения для непрерывной случайной величины будет иметь вид
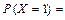
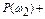
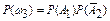
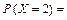
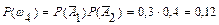
(Проверим, что 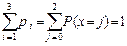
Ряд распределения данной случайной величины X имеет вид
| xi | Итого | ||
| pi | 0,42 | 0,46 | 0,12 |
Столбцовая диаграмма, соответствующая этому ряду распределения, приведена на рисунке 9.
Вычислим функцию распределения данной случайной величины:
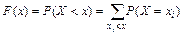
при x Î (- ¥, 0] 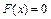
при x Î (0, 1] 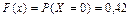
при x Î (1, 2] 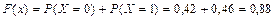
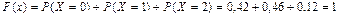
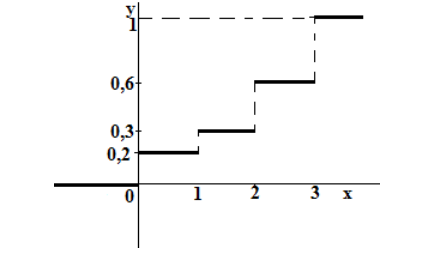
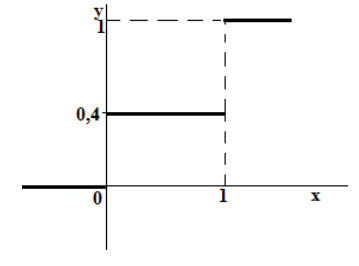
Итак, функция распределения рассматриваемой случайной величины имеет вид:
График функции F(x) приведён на рисунке 10.
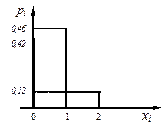 | 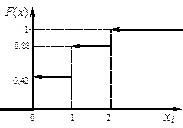 |
| Рисунок 9 – Столбцовая диаграмма | Рисунок 10 – Функция распределения |
Функция плотности распределения вероятностей непрерывной случайной величины.
Плотностью распределения вероятностей непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке:
По своему смыслу значения функции f(x) пропорциональны вероятности того, что исследуемая случайная величина примет значение где-то в непосредственной близости от точки x.
Функция плотности распределения f(x), как и функция распределения F(x), является одной из форм задания закона распределения, но она применима только для непрерывных случайных величин. Функцию плотности распределения вероятностей f(x) еще называют дифференциальной функцией распределения, тогда как функцию распределения F(x) называют, соответственно, интегральной функцией распределения.
График функции плотности распределения f(x) называется кривой распределения.
Рассмотрим свойства, которыми обладает функция плотности распределения непрерывной случайной величины.
Свойство 1. Плотность распределения вероятностей – неотрицательная функция:
(геометрически: кривая распределения лежит не ниже оси абсцисс).
Свойство 2. Вероятность попадания значения случайной величины на участок от a до b определяется по формуле
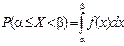
(геометрически: эта вероятность равна площади криволинейной трапеции, ограниченной кривой f(x), осью Ох и прямыми x = a и x = b).
Свойство 3.
(геометрически: площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице).
В частности, если все возможные значения случайной величины принадлежат отрезку [a, b], то
Свойство 4. Функция распределения F(x) может быть найдена по известной функции плотности распределения следующим образом:
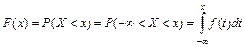
Пример 27. Непрерывная случайная величина задана функцией распределения
Определить дифференциальную функцию плотности распределения.
Решение. Определим дифференциальную функцию плотности распределения
Пример 28. Является ли плотностью распределения некоторой случайной величины каждая из следующих функций?
а) 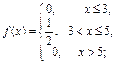
в)
Решение. а) Проверим справедливость свойства 3:
В данном случае имеем
Функция неотрицательна для всех x. То есть заданная функция является функцией плотности распределения некоторой случайной величины.
б) Заданная функция не является плотностью распределения некоторой случайной величины, так как 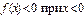
в) Проверим справедливость свойства 3:
В данном случае имеем
Функция неотрицательна для всех 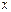
Вопросы для самоконтроля
1. Что называется случайной величиной?
2. Какие величины называются дискретными? непрерывными?
3. Что называется законом распределения случайной величины?
4. Какими способами может быть задан закон распределения дискретной случайной величины? непрерывной?
5. Что характеризует функция распределения F(x) случайной величины?
6. Как определить вероятность попадания значения случайной величины в некоторый интервал с помощью функции распределения?
7. Что характеризует функция плотности распределения случайной величины? Укажите ее вероятностный смысл.
8. Для каких величин определена функция плотности распределения?
9. Может ли функция плотности распределения принимать отрицательные значения?
10. Как связаны между собой функции F(x) и f(x)?
11. Какие случайные величины называются непрерывными?
12. Чему равна площадь фигуры, ограниченной кривой распределения и осью абсцисс?
13. Как определить вероятность попадания значения непрерывной случайной величины в некоторый интервал с помощью функции плотности распределения?
Что показывает функция распределения случайной величины
(F2) cХЭЕУФЧХАФ РТЕДЕМЩ Й ; (F3) ПОБ Ч МАВПК ФПЮЛЕ ОЕРТЕТЩЧОБ УМЕЧБ:
фПЮОП ФБЛ ЦЕ ДПЛБЦЕН ПУФБМШОЩЕ УЧПКУФЧБ.
(F4) ч МАВПК ФПЮЛЕ ТБЪОЙГБ ТБЧОБ :
(F5) дМС МАВПК УМХЮБКОПК ЧЕМЙЮЙОЩ ЙНЕЕФ НЕУФП ТБЧЕОУФЧП:
йЪ УЧПКУФЧ (F4) Й (F5) РПМХЮБЕН УМЕДХАЭЕЕ УЧПКУФЧП.
рПУЛПМШЛХ ЖХОЛГЙС ТБУРТЕДЕМЕОЙС ПДОПЪОБЮОП ПРТЕДЕМСЕФ ТБУРТЕДЕМЕОЙЕ УМХЮБКОПК ЧЕМЙЮЙОЩ ( ЬФХ ЖТБЪХ УФПЙФ ЛБЛ УМЕДХЕФ ПВДХНБФШ!), НПЦОП УЮЙФБФШ ЧПЪНПЦОПУФШ РТЕДУФБЧЙФШ ЖХОЛГЙА ТБУРТЕДЕМЕОЙС ЙОФЕЗТБМПН (14) ПФ ОЕПФТЙГБФЕМШОПК ЖХОЛГЙЙ ПРТЕДЕМЕОЙЕН БВУПМАФОП ОЕРТЕТЩЧОПЗП ТБУРТЕДЕМЕОЙС.
(f3) еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ БВУПМАФОП ОЕРТЕТЩЧОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ЕЈ ЖХОЛГЙС ТБУРТЕДЕМЕОЙС ЧУАДХ ОЕРТЕТЩЧОБ.
ьФПФ ЖБЛФ УМЕДХЕФ ЙЪ УЧПКУФЧБ 7 Й ЙЪ (F4). ъБНЕФЙН, ЮФП (f3) ЕУФШ ФБЛЦЕ УМЕДУФЧЙЕ РТЕДУФБЧМЕОЙС (14) Й ОЕРТЕТЩЧОПУФЙ ЙОФЕЗТБМБ ЛБЛ ЖХОЛГЙЙ ЧЕТИОЕЗП РТЕДЕМБ.
(f4) еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ БВУПМАФОП ОЕРТЕТЩЧОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ЕЈ ЖХОЛГЙС ТБУРТЕДЕМЕОЙС ДЙЖЖЕТЕОГЙТХЕНБ РПЮФЙ ЧУАДХ, Й
пРЙТБСУШ ОБ УЧПКУФЧБ (f4) Й (14), НПЦОП УЖПТНХМЙТПЧБФШ ФБЛПК ЛТЙФЕТЙК БВУПМАФОПК ОЕРТЕТЩЧОПУФЙ ТБУРТЕДЕМЕОЙС: ТБУРТЕДЕМЕОЙЕ У ЖХОЛГЙЕК ТБУРТЕДЕМЕОЙС БВУПМАФОП ОЕРТЕТЩЧОП, ЕУМЙ РТЙ ЧУЕИ ЙНЕЕФ НЕУФП ТБЧЕОУФЧП:
йЪ ПРТЕДЕМЕОЙС БВУПМАФОП ОЕРТЕТЩЧОПЗП ТБУРТЕДЕМЕОЙС Й УЧПКУФЧБ 7 УТБЪХ УМЕДХЕФ УЧПКУФЧП:
(f5) еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ БВУПМАФОП ОЕРТЕТЩЧОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ДМС МАВЩИ ЙНЕАФ НЕУФП ТБЧЕОУФЧБ:
рТЙНЕТПН ФБЛПК ЖХОЛГЙЙ ТБУРТЕДЕМЕОЙС УМХЦЙФ МЕУФОЙГБ лБОФПТБ:
Содержание:
Законы распределения:
Распределение случайных переменных: Каждая из случайных переменных имеет ряд возможных значений, могущих возникнуть с определенной вероятностью.
Случайные переменные величины могут носить прерывный (дискретный) и непрерывный характер. Возможные значения прерывной случайной переменной отделены друг от друга конечными интервалами. Возможные значения непрерывной случайной переменной не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.
Примерами прерывных случайных переменных могут служить:
Примеры непрерывных случайных переменных:
Если перечислить все возможные значения случайной переменной и указать вероятности этих значений, то получится распределение случайной переменной. Распределение случайной переменной указывает на соотношение между отдельными значениями случайной величины и их вероятностями.
Распределение случайной переменной будет задано законом распределения, если точно указать, какой вероятностью обладает каждое значение случайной переменной.
Такая таблица называется также рядом распределения случайной переменной.
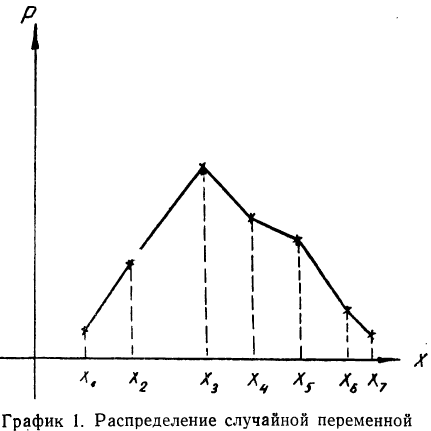
Для наглядности ряд распределения изображают графически, откладывая на прямоугольной системе координат по оси абсцисс возможные значения случайной переменной, а по оси ординат — их вероятности. В результате графического изображения получается многоугольник или полигон распределения (график 1). Многоугольник распределения является одной из форм закона распределения.
Функция распределения
Ряд распределения является исчерпывающей характеристикой прерывной случайной перемен-
Вероятность того, что Х
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Определение функции распределения
Вы будете перенаправлены на Автор24
Определение функции распределения
Также иначе функцию распределения иногда называются интегральной функцией распределения или интегральным законом распределения.
Рисунок 1. Пример графика функции распределения
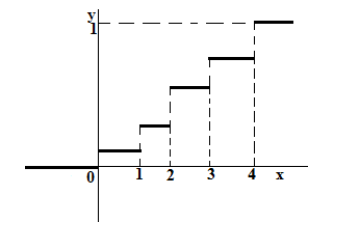
Функция распределения дискретной случайной величины
Функция распределения непрерывной случайной величины
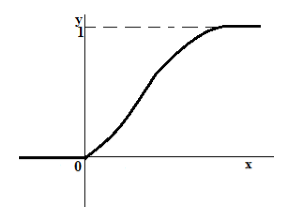
График функции распределения такой случайной величины всегда представляет собой неубывающую непрерывную функцию (рис. 3).
Готовые работы на аналогичную тему
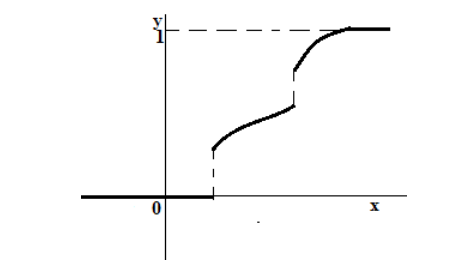
Функция распределения смешанной случайной величины
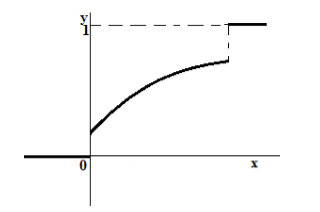
График функции распределения такой случайной величины всегда представляет собой неубывающую функцию, которая имеет минимальное значение в 0, максимальное значение в 1, но которая не на всей области определения является непрерывной функцией (то есть имеет скачки в отдельных точках) (рис. 4).
Рисунок 4. Функция распределения смешанной случайной величины
Примеры задач на нахождение функции распределения
Найти функцию распределения вероятностей и построить её график.
Решение.
Отсюда получаем следующую функцию распределения вероятностей:
Построим ее график:
Решение.
Построим для начала ряд распределения данной случайной величины:
Так как случайная величина является дискретной, найдем функцию распределения по аналогии с задачей 1:
Таким образом, получаем следующую функцию распределения:
Построим ее график:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 20 02 2021