Что показывает гистограмма в статистике

6 причин, по которым вам следовало бы отказаться от гистограмм

Гистограммам не чужды систематические ошибки. Дело в том, что они достаточно условны и могут привести к неправильным выводам о данных. Если вы хотите визуализировать переменную, лучше выбрать другой график.

Независимо от того, находитесь ли вы на встрече с высшим руководящим составом или со специалистами по обработке данных, в одном вы можете быть уверены: в какой-то момент появится гистограмма.

И нетрудно догадаться почему. Гистограммы весьма интуитивно наглядны: любой поймет их с первого взгляда. Более того, они объективно представляют реальность, не так ли? А вот и нет.

Гистограмма может ввести в заблуждение и привести к ошибочным выводам — ​​даже на простейшем наборе данных!

В этой статье мы на примерах рассмотрим 6 причин, почему, когда дело доходит до визуализации данных, гистограммы точно не является лучшим выбором:

Они слишком сильно зависят от количества интервалов.

Они слишком сильно зависят от максимума и минимума переменной.

Они не дают возможности заметить значимые значения переменной.

Они не позволяют отличить непрерывные переменные от дискретных.

Они делают сравнение распределений сложным.

Их построение затруднено, если в памяти находятся не все данные.

«Ладно, я понял: гистограммы не идеальны. Но есть ли у меня выбор?» Конечно есть!

В конце статьи я порекомендую другой график, называемый CDP, который минует эти недостатки.

Итак, что же не так с гистограммой?

1. Она слишком сильно зависит от количества интервалов.

Чтобы построить гистограмму, вы должны сначала определить количество интервалов, также называемых корзинами (bins). Для этого существует множество различных практических методов (вы можете ознакомиться с их обзором на этой странице). Но насколько критичен этот выбор? Давайте возьмем реальные данные и посмотрим, как меняется гистограмма в зависимости от количества интервалов.

Переменная представляет собой максимальную частоту сердечных сокращений (ударов в минуту), полученную у 303 людей во время некоторой физической активности (данные взяты из набора данных UCI по сердечным заболеваниям: источник).

Как изменяется гистограмма при изменении количества интервалов. [Рисунок автора]

Глядя на верхний левый график (который мы получим по умолчанию в Python и R), у нас сложится впечатление хорошего распределения с одним пиком (модой). Однако если бы мы рассмотрели бы другие варианты гистограммы, мы получили бы совершенно другую картину. Разные гистограммы одних и тех же данных могут привести к противоречивым выводам.

2. Она слишком сильно зависит от максимума и минимума переменной.

Даже после того, как количество интервалов установлено, интервалы зависят от положения минимума и максимума переменной. Достаточно, чтобы один из них немного изменился, и все интервалы также изменятся. Другими словами, гистограммы не являются надежными.

Например, давайте попробуем изменить максимум переменной, не меняя количество интервалов.

Как меняется гистограмма при изменении максимального значения. [Рисунок автора]

Отличается только одно значение, а весь график получается другим. Это нежелательное свойство, потому что нас интересует общее распределение: одно значение не должно так влиять на график!

3. Не дает возможности заметить значимые значения переменной.

Если в общем, то когда переменная содержит некоторые часто повторяющиеся значения, нам конечно нужно об этом знать. Однако гистограммы этому препятствуют, поскольку они основаны на интервалах, а интервалы «скрывают» отдельные значения.

Классическим примером является случай, когда отсутствующим значениям массово присваивается 0. В качестве примера давайте рассмотрим набор данных переменной, состоящий из 10 тысяч значений, 26% из которых — нули.

Те же данные, разная ширина интервала. На левом графике невозможно обнаружить высокую концентрацию нулей. [Рисунок автора]

График слева — это то, что вы получаете по умолчанию в Python. Глядя на него, вы не заметите скопление нулей, и вы даже можете подумать, что эта переменная имеет «плавную» динамику.

График справа получен путем сужения интервалов и дает более четкое представление о реальности. Но дело в том, что как бы вы ни сужали интервалы, вы никогда не будете уверены, содержит ли первый интервал только 0 или какие-то другие значения.

4. Не позволяет отличить непрерывные переменные от дискретных.

Зачастую мы бы хотели знать, является ли числовая переменная непрерывной или дискретной. По гистограмме это практически невозможно сказать.

Возьмем переменную «Возраст» (Age). Вы можете получить Возраст = 49 лет (когда возраст округлен) или Возраст = 49,828884325804246 лет (когда возраст рассчитывается как количество дней с момента рождения, деленное на 365,25). Первая — дискретная переменная, вторая — непрерывная.

Слева непрерывная переменная. Справа дискретная переменная. Однако на верхних графиках они выглядят одинаково. [Рисунок автора]

Тот, что слева, непрерывен, а тот, что справа, дискретен. Однако на верхних графиках (по умолчанию в Python) вы не увидите никакой разницы между ними: они выглядят совершенно одинаково.

5. Сложно сравнивать распределения.

Часто бывает необходимо сравнить одну и ту же переменную в разных кластерах. Например, в отношении данных UCI о сердечных заболеваниях, приведенных выше, мы можем сравнить:

все население (для справки)

люди моложе 50 страдающие сердечными заболеваниями

люди моложе 50 НЕ страдающие сердечными заболеваниями

люди старше 60 лет страдающие сердечными заболеваниями

люди старше 60 и НЕ страдающие сердечными заболеваниями.

Вот что мы получили бы в итоге:

Сравнение гистограмм. [Рисунок автора]

Гистограммы основаны на областях, и, когда мы пытаемся провести сравнение, области в конечном итоге перекрываются, что делает эту задачу практически невыполнимой.

6. Сложно построить, если в памяти находятся не все данные.

Если все ваши данные находятся в Excel, R или Python, построить гистограмму легко: в Excel вам просто нужно кликнуть по иконке гистограммы, в R — выполнить команду hist(x), а в Python — plt.hist(х).

Но предположим, что ваши данные хранятся в базе данных. Вы же не хотите выгружать все данные только для того, чтобы построить гистограмму, верно? По сути, все, что вам нужно, это таблица, содержащая для каждого интервала крайние значения и количество наблюдений. Примерно такая:

| INTERVAL_LEFT | INTERVAL_RIGHT | COUNT |

| 75.0 | 87.0 | 31 |

| 87.0 | 99.0 | 52 |

| 99.0 | 111.0 | 76 |

Но получить ее с помощью SQL-запроса не так просто, как кажется. Например, в Google Big Query код будет выглядеть так:

Немного громоздко, не правда ли?

Альтернатива: график кумулятивного распределения.

График кумулятивного распределения — это график квантилей переменной. Другими словами, каждая точка CDP показывает:

по оси x: исходное значение переменной (как в гистограмме);

по оси y: сколько наблюдений имеют такое же или меньшее значение.

Давайте посмотрим на пример с переменной — максимальной частотой пульса.

График кумулятивного распределения максимальной частоты сердечных сокращений. [Рисунок автора]

Возьмем точку с координатами x = 140 и y = 90 (30%). По горизонтальной оси вы видите значение переменной: 140 ударов сердца в минуту. По вертикальной оси вы видите количество наблюдений, у которых частота сердцебиение равна или ниже 140 (в данном случае 90 человек, что означает 30% выборки). Следовательно, у 30% нашей выборки максимальная частота сердцебиения составляет 140 или менее ударов в минуту.

Какой смысл в графике, показывающем, сколько наблюдений «равно или ниже» заданного уровня? Почему не просто «равно»? Потому что в противном случае результат зависел бы от отдельных значений переменной. И это не сработает, потому что каждое значение имеет очень мало наблюдений (обычно только одно, если переменная непрерывна). Напротив, CDP полагаются на квантили, которые более стабильны, выразительны и легко читаются.

Вдобавок CDP намного полезнее. Если задуматься, вам часто приходится отвечать на такие вопросы, как «у скольких из них от 140 до 160?» Или «у скольких из них больше 180?». Имея перед глазами CDP, вы можете дать немедленный ответ. С гистограммой это было бы невозможно.

CDP решает все проблемы, которые мы видели выше. Фактически, по сравнению с гистограммой:

1. Не требует пользовательского выбора. Для одного набора данных, существует только один возможный CDP.

2. Не страдает от выпадающих значений. Экстремальные значения не влияют на CDP, поскольку квантили не меняются.

3. Позволяет определять значимые значения. Если существует концентрация точек данных на каком-то конкретном значении, это сразу видно, поскольку будет вертикальный сегмент, соответствующий значению.

4. Позволяет с первого взгляда распознать дискретную переменную. Если существует только конкретный набор возможных значений (т.е. переменная дискретна), это сразу видно, поскольку кривая примет форму лестницы.

5. Упрощает сравнение распределений. На одном графике легко сравнить два или более распределения, поскольку это просто кривые, а не области. Кроме того, ось y всегда находится в диапазоне от 0 до 100%, что делает сравнение еще более простым. Для сравнения, это пример, который мы видели выше:

Сравнение распределений в CDP. [Рисунок автора]

6. Его легко построить, даже если у вас нет всех данных в памяти. Все, что вам нужно, это квантили, которые можно легко получить с помощью SQL:

Как построить график кумулятивного распределения в Excel, R, Python

В R это делается в одну строчку:

Спасибо за внимание! Надеюсь, эта статья оказалась для вас полезной.

Я ценю отзывы и конструктивную критику. Если вы хотите поговорить об этой статье или других связанных темах, вы можете написать мне в Linkedin.

Перевод материала подготовлен в рамках онлайн-курса «Machine Learning. Basic«. Всех заинтересованных приглашаем на день открытых дверей курса, где можно будет узнать все подробности об обучении и пообщаться с преподавателем.

Источник

3. Интервальный вариационный ряд.
Гистограмма относительных частот

На предыдущем уроке по математической статистике (Занятие 1) мы разобрали дискретный вариационный ряд (Занятие 2), и сейчас на очереди интервальный. Его понятие, графическое представление (гистограмма и эмпирическая функция распределения), а также рациональные методы вычислений, как ручные, так и программные. В том числе будут рассмотрены задачи с достаточно большим количеством (100-200) вариант – что делать в таких случаях, как обработать большой массив данных.

Предпосылкой построения интервального вариационного ряда (ИВР) является тот факт, что исследуемая величина принимает слишком много различных значений. Зачастую ИВР появляется в результате измерения непрерывной характеристики изучаемых объектов. Типично – это время, масса, размеры и другие физические характеристики. Подходящие примеры встретились в первой же статье по матстату, вспоминаем Константина, который замерял время на лабораторной работе и Фёдора, который взвешивал помидоры.

Для изучения интервального вариационного ряда затруднительно либо невозможно применить тот же подход, что и для дискретного ряда. Это связано с тем, что ВСЕ варианты многих ИВР различны. И даже если встречаются совпадающие значения, например, 50 грамм и 50 грамм, то связано это с округлением, ибо полученные значения всё равно отличаются хоть какими-то микрограммами.

Поэтому для исследования ИВР используется другой подход, а именно, определяется интервал, в пределах которого варьируются значения, затем данный интервал делится на частичные интервалы, и по каждому интервалу подсчитываются частоты – количество вариант, которые в него попали.

Разберём всю кухню на конкретной задаче, и чтобы как-то разнообразить физику, я приведу пример с экономическим содержанием, кои десятками предлагают студентам экономических отделений. Деньги, строго говоря, дискретны, но если надо, непрерывны :), и по причине слишком большого разброса цен, для них целесообразно строить интервальный ряд:

По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные (в некоторых денежных единицах):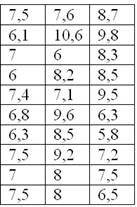

Требуется составить вариационный ряд распределения, построить гистограмму и полигон относительных частот + бонус – эмпирическую функцию распределения.

Такое обывательское исследование проводит каждый из нас, начиная с анализа цены на пакет молока вот это дожил в нескольких магазинах, и заканчивая ценами на недвижимость по гораздо бОльшей выборке. Что называется, не какие-то там унылые сантиметры.

Поэтому представьте свой любимый товар / услугу и наслаждайтесь решением🙂

Очевидно, что перед нами выборочная совокупность объемом 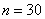наблюдений (таблица 10*3), и вопрос номер один: какой ряд составлять – дискретный или интервальный? Смотрим на таблицу: среди предложенных цен есть одинаковые, но их разброс довольно велик, и поэтому здесь целесообразно провести интервальное разбиение. К тому же цены могут быть округлёнными.

Начнём с экстремальной ситуации, когда у вас под рукой нет Экселя или другого подходящего программного обеспечения. Только ручка, карандаш, тетрадь и калькулятор.

Тактика действий похожа на исследование дискретного вариационного ряда. Сначала окидываем взглядом предложенные числа и определяем примерный интервал, в который вписываются эти значения. «Навскидку» все значения заключены в пределах от 5 до 11. Далее делим этот интервал на удобные подынтервалы, в данном случае напрашиваются промежутки единичной длины. Записываем их на черновик:

Теперь начинаем вычёркивать числа из исходного списка и записывать их в соответствующие колонки нашей импровизированной таблицы: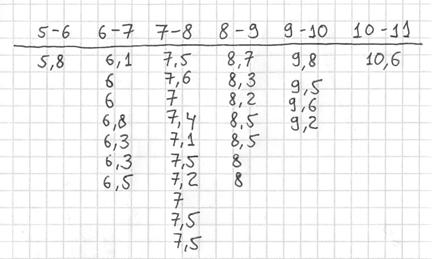

После этого находим самое маленькое число в левой колонке и самое большое значение – в правой. Тут даже ничего искать не пришлось, честное слово, не нарочно получилось:)
ден. ед. – хорошим тоном считается указывать размерность.

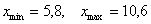
Вычислим размах вариации:
ден. ед. – длина общего интервала, в пределах которого варьируется цена.

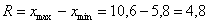
Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на этот счёт существует формула Стерджеса:

, где – десятичный логарифм* от объёма выборки и – оптимальное количество интервалов, при этом результат округляют до ближайшего левого целого значения.

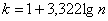
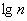
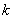
* есть на любом более или менее приличном калькуляторе

В нашем случае получаем:
интервалов.

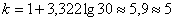
Следует отметить, что правило Стерджеса носит рекомендательный, но не обязательный характер. Нередко в условии задачи прямо сказано, на какое количество интервалов нужно проводить разбиение (на 4, 5, 6, 10 и т.д.), и тогда следует придерживаться именно этого указания.

Длины частичных интервалов могут быть различны, но в большинстве случаев использует равноинтервальную группировку:
– длина частичного интервала. В принципе, здесь можно было не округлять и использовать длину 0,96, но удобнее, ясен день, 1.

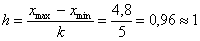
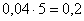
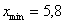
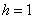
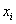
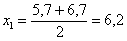
И коль скоро мы прибавили 0,04, то по 5 частичным интервалам у нас получается «перебор»: . Посему от самой малой варианты отмеряем влево 0,1 влево (половину «перебора») и к значению 5,7 начинаем прибавлять по , получая тем самым частичные интервалы. При этом сразу рассчитываем их середины (например, ) – они требуются почти во всех тематических задачах:

– убеждаемся в том, что самая большая варианта 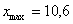вписалась в последний частичный интервал и отстоит от его правого конца на 0,1.

Далее подсчитываем частоты по каждому интервалу. Для этого в черновой «таблице» обводим значения, попавшие в тот или иной интервал, подсчитываем их количество и вычёркиваем: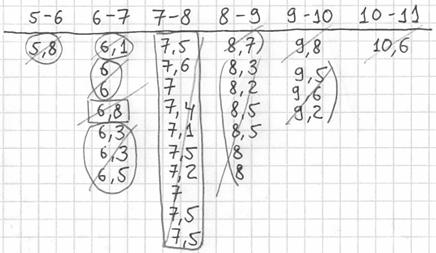

Так, значения из 1-го интервала я обвёл овалами (7 штук) и вычеркнул, значения из 2-го интервала – прямоугольниками (11 штук) и вычеркнул и так далее.

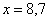
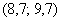
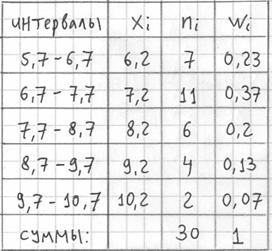
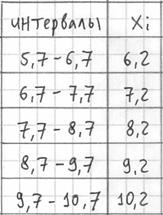
Правило: если варианта попадает на «стык» интервалов, то её следует относить в правый интервал. У нас такая варианта встретилась одна: – и её нужно причислить к интервалу .

В результате получаем интервальный вариационный ряд, при этом обязательно убеждаемся в том, что ничего не потеряно: 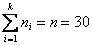, и, кроме того, рассчитываем относительные частоты по каждому интервалу, которые уместно округлить до двух знаков после запятой:

Дело за чертежами. Для ИВР чаще всего требуется построить гистограмму.

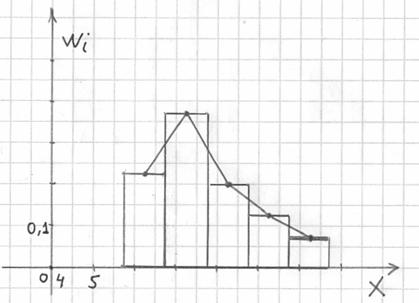
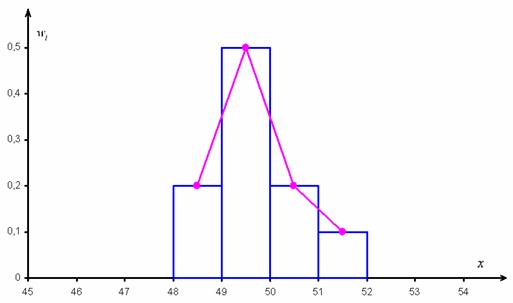
Гистограмма относительных частот – это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов, а высота – соответствующим относительным частотам: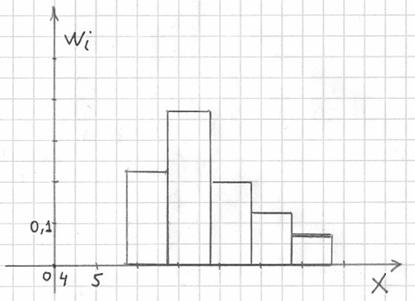

При этом вполне допустимо использовать нестандартную шкалу по оси абсцисс, в данном случае я начал нумерацию с четырёх.

Площадь гистограммы равна единице, и это статистический аналог функции плотности распределения непрерывной случайной величины. Построенный чертёж даёт наглядное и весьма точное представление о распределении цен на ботинки по всей генеральной совокупности. Но это при условии, что выборка представительна.

Вместе с гистограммой нередко требуют построить полигон. Без проблем, полигон относительных частот – это ломаная, соединяющая соседние точки 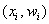, где – середины интервалов:

Автоматизируем решение в Экселе:

Как составить ИВР и представить его графически? (Ютуб)

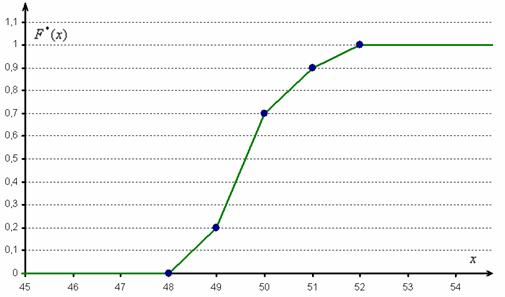
И бонус – эмпирическая функция распределения. Она определяется точно так же, как в дискретном случае:

, где – количество вариант СТРОГО МЕНЬШИХ, чем «икс», который «пробегает» все значения от «минус» до «плюс» бесконечности.

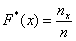
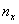
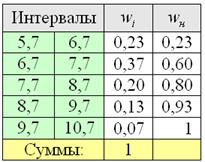
Но вот построить её для интервального ряда намного проще. Находим накопленные относительные частоты:

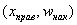
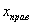
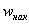
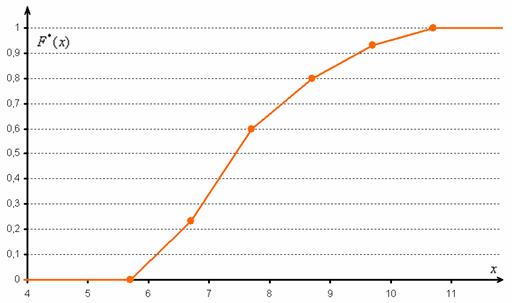
И строим кусочно-ломаную линию, с промежуточными точками , где – правые концы интервалов, а – относительная частота, которая успела накопиться на всех «пройденных» интервалах:

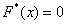
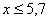
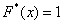
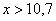
При этом если и если .

Напоминаю, что данная функция не убывает, принимает значения из промежутка 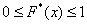и, кроме того, для ИВР она ещё и непрерывна.

Эмпирическая функция распределения является аналогом функции распределения НСВ и приближает теоретическую функцию 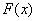, которую теоретически, а иногда и практически можно построить по всей генеральной совокупности.

Помимо перечисленных графиков, вариационные ряды также можно представить с помощью кумуляты и огивы частот либо относительных частот, но в классическом учебном курсе эта дичь редкая, и поэтому о ней буквально пару абзацев:

Кумулята – это ломаная, соединяющая точки:

* либо – для дискретного вариационного ряда;
либо – для интервального вариационного ряда.

* – накопленные «обычные» частоты

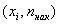
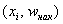
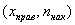
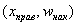
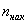
В последнем случае кумулята относительных частот 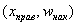представляет собой «главный кусок» недавно построенной эмпирической функции распределения.

Огива – это обратная функция по отношению к кумуляте – здесь варианты откладываются по оси ординат, а накопленные частоты либо относительные частоты – по оси абсцисс.

С построением данных линий, думаю, проблем быть не должно, чего не скажешь о другой проблеме. Хорошо, если в вашей задаче всего лишь 20-30-50 вариант, но что делать, если их 100-200 и больше? В моей практике встречались десятки таких задач, и ручной подсчёт здесь уже не торт. Считаю нужным снять небольшое видео:

Как быстро составить ИВР при большом объёме выборки? (Ютуб)

Ну, теперь вы монстры 8-го уровня 🙂

Но не всё так сурово. В большинстве задач вам предложат готовый вариационный ряд, и на счёт молока, то, конечно, была шутка:

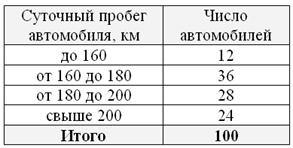
Выборочная проверка партии чая, поступившего в торговую сеть, дала следующие результаты:

Требуется построить гистограмму и полигон относительных частот, эмпирическую функцию распределения

Проверяем свои навыки работы в Экселе! (исходные числа и краткая инструкция прилагается) И на всякий случай краткое решение для сверки в конце урока.

Что ещё важного по теме? Время от времени встречаются ИВР с открытыми крайними интервалами, например:

В таких случаях, что убийственно логично, интервалы «закрывают». Обычно поступают так: сначала смотрим на средние интервалы и выясняем длину частичного интервала: 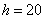км. И для дальнейшего решения можно считать, что крайние интервалы имеют такую же длину: от 140 до 160 и от 200 до 220 км. Тоже логично. Но уже не убийственно:)

Ну вот, пожалуй, и вся практически важная информация по ИВР.

На очереди числовые характеристики вариационных рядов и начнём мы с их центральных характеристик, а именно – Моды, медианы и средней.

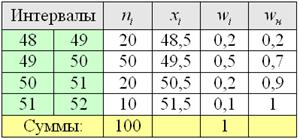
Пример 7. Решение: заполним расчётную таблицу

Построим гистограмму и полигон относительных частот:

Построим эмпирическую функцию распределения:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник