Что показывает гистограмма распределения
Гистограмма распределения в EXCEL
history 15 ноября 2016 г.
Гистограмма поможет визуально оценить распределение набора данных, если:
Примечание : Для удобства написания формул для диапазона А8:А57 создан Именованный диапазон Исходные_данные.
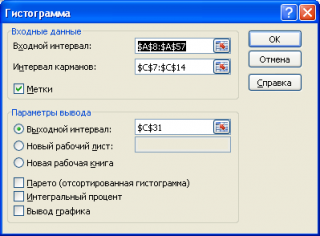
Построение гистограммы с помощью надстройки Пакет анализа
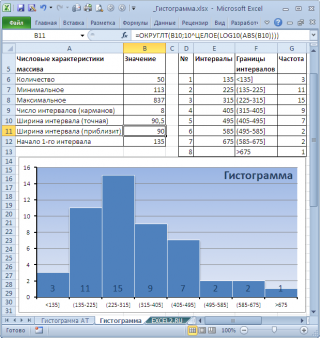
Как видно из рисунка, первый интервал включает только одно минимальное значение 113 (точнее, включены все значения меньшие или равные минимальному). Если бы в массиве было 2 или более значения 113, то в первый интервал попало бы соответствующее количество чисел (2 или более).
Почему 7? Дело в том, что количество интервалов гистограммы (карманов) зависит от количества данных и для его определения часто используется формула √n, где n – это количество данных в выборке. В нашем случае √n=√50=7,07 (всего 7 полноценных карманов, т.к. первый карман включает только значения равные минимальному).
Примечание : Похоже, что инструмент Гистограмма для подсчета общего количества интервалов (с учетом первого) использует формулу =ЦЕЛОЕ(КОРЕНЬ(СЧЕТ( Исходные_данные )))+1
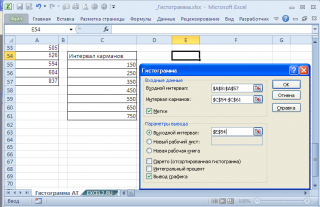
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля Метка ). 
Для нашего набора данных установим размер кармана равным 100 и первый карман возьмем равным 150. 
Построение гистограммы распределения без использования надстройки Пакет анализа
Порядок действий при построении гистограммы в этом случае следующий:
В итоге можно добиться вот такого результата. 
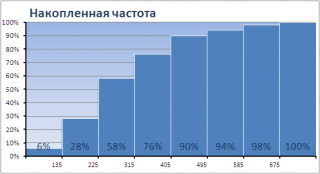
Одной из разновидностей гистограмм является график накопленной частоты (cumulative frequency plot). 
На этом графике каждый столбец представляет собой число значений исходного массива, меньших или равных правой границе соответствующего интервала. Это очень удобно, т.к., например, из графика сразу видно, что 90% значений (45 из 50) меньше чем 495.
Примечание : Когда количество значений в выборке недостаточно для построения полноценной гистограммы может быть полезна Блочная диаграмма (иногда она называется Диаграмма размаха или Ящик с усами ).
Нормальное распределение: понимание гистограмм и вероятностей
В данной статье мы продолжаем исследование нормального распределения, рассматривая концепцию гистограмм и вводя функцию массы вероятности.
Данная статья является частью серии статей о статистике в электротехнике, которую мы начали с обсуждения статистического анализа и описательной статистики. Затем мы исследовали три описательных статистических показателя с точки зрения применения в обработке сигналов.
В прошлой статье мы представили нормальное распределение в электротехнике, заложив основу для нашего текущего обсуждения: понимание вероятностей в измеренных данных.
Понимание гистограмм
В предыдущей статье мы начали обсуждение нормального распределения, обратившись к форме этой гистограммы:
Рисунок 1 – Гистограмма, иллюстрирующая нормальное или гауссово распределение
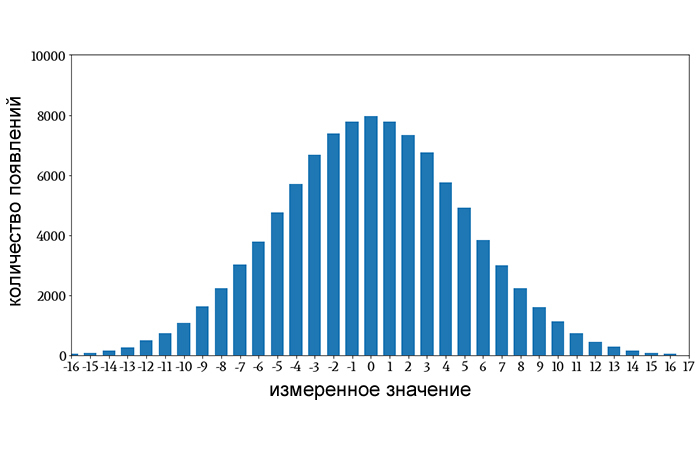
Я думаю, что большинство людей, работающих в области науки или техники, хотя бы смутно знакомы с гистограммами, но давайте сделаем шаг назад.
Что такое гистограмма?
Гистограммы – это визуальные представления 1) значений, присутствующих в наборе данных, и 2) частоты появления этих значений. Показанная выше гистограмма может представлять множество различных типов информации.
Представим, что она представляет собой распределение значений, полученных нами при измерении разницы, округленной до ближайшего милливольта, между номинальным и фактическим выходным напряжением линейного стабилизатора, который подвергался различным температурам и условиям эксплуатации. Так, например, примерно 8000 измерений показали разницу в 0 мВ между номинальным и фактическим выходными напряжениями, а примерно 1000 измерений показали разницу в 10 мВ.
Гистограммы – чрезвычайно эффективный способ обобщения больших объемов данных. Взглянув на гистограмму выше, мы можем быстро найти частоту отдельных значений в наборе данных и определить тенденции или закономерности, которые помогут нам понять взаимосвязь между измеренным значением и частотой.
Гистограммы с интервалами
Когда набор данных содержит так много разных значений, что мы не можем удобно связать их с отдельными столбцами гистограммы, мы используем объединение в интервалы (биннинг). То есть мы определяем диапазон значений как интервал, группируем результаты измерений в эти интервалы и создаем по одному столбцу для каждого интервала.
Следующая гистограмма, которая была сгенерирована из нормально распределенных данных со средним значением 0 и стандартным отклонением 0,6, использует интервалы вместо отдельных значений:
Рисунок 2 – Гистограмма с использованием интервалов вместо отдельных значений
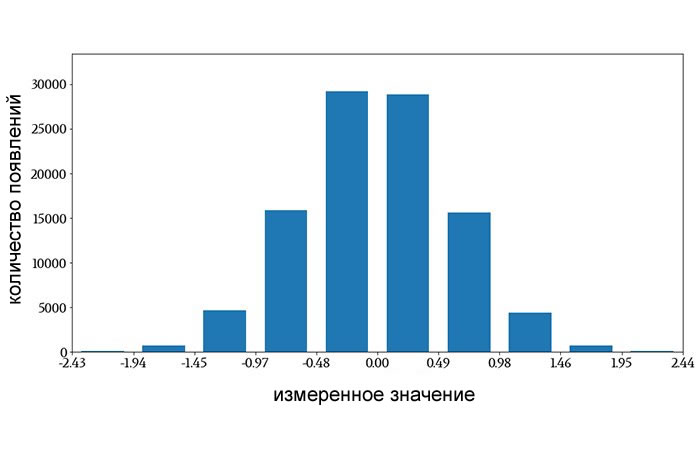
Горизонтальная ось разделена на десять интервалов одинаковой ширины, и каждому интервалу назначен один столбец. Все результаты измерений, попадающие в числовой интервал, влияют на высоту соответствующего столбца (метки на горизонтальной оси показывают, что интервалы не одинаковой ширины, но это просто потому, что значения меток округлены).
Гистограммы и вероятность
В некоторых ситуациях гистограмма не дает нужной нам информации. Мы можем посмотреть на гистограмму и легко определить частоту измеренного значения, но не можем легко определить вероятность измеренного значения.
Например, если я посмотрю на первую гистограмму, я знаю, что примерно 8000 измерений показали разницу в 0 В между номинальным и фактическим напряжениями стабилизатора, но я не знаю, какова вероятность того, что результат случайно выбранного измерения или нового измерения сообщит о разнице в 0 В.
Это серьезное ограничение, потому что вероятность отвечает на чрезвычайно распространенный вопрос: каковы шансы, что…?
Причина этого ограничения заключается в том, что гистограмма просто четко не передает размер выборки, то есть общее количество измерений (теоретически общее количество измерений можно определить, сложив значения всех столбцов гистограммы, но это было бы утомительно и неточно).
Если мы знаем размер выборки, мы можем разделить количество появлений на размер выборки и таким образом определить вероятность. Давайте рассмотрим пример.
Рисунок 3 – Пример того, как гистограмма может помочь нам определить вероятность путем деления количества появлений на размер выборки
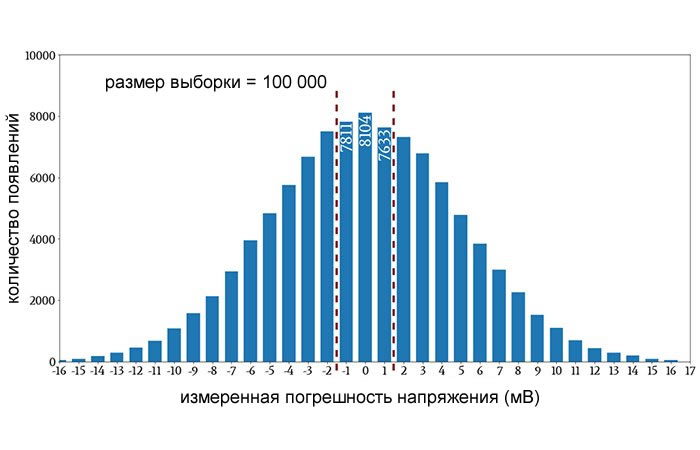
Красные пунктирные линии заключают в себя столбцы, которые указывают на погрешности напряжения менее 2 мВ, а числа, написанные внутри столбцов, указывают точное количество появлений этих трех значений погрешности напряжения. Сумма этих трех чисел составляет 23 548. Таким образом, на основе этого примера по сбору данных вероятность получения погрешности менее 2 мВ составляет 23 548/100 000 ≈ 23,5%.
Функция массы вероятности
Если наша основная цель при создании гистограммы – передать информацию о вероятности, мы можем изменить всю гистограмму, разделив все счетчики вхождений на размер выборки.
Полученный график является аппроксимацией функции массы вероятности. Например:
Рисунок 4 – Гистограмма, изображающая приблизительную функцию массы вероятности, полученную путем деления количества всех вхождений на размер выборки
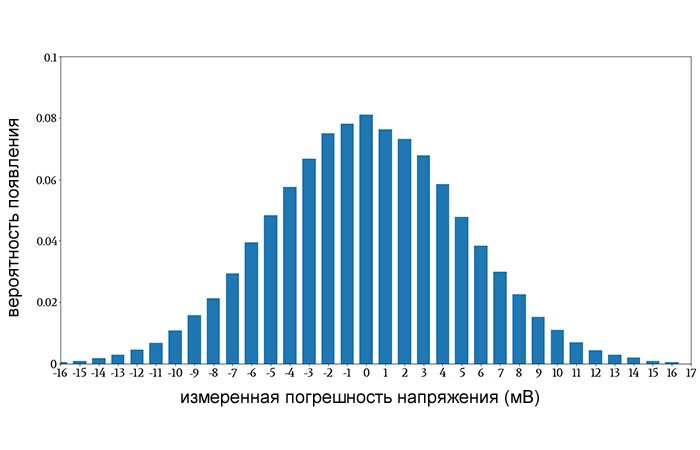
Всё, что мы на самом деле выполнили, это изменили числа на вертикальной оси. Тем не менее, теперь мы можем посмотреть на отдельное значение или на группу значений и легко определить вероятность появления.
Хочу прояснить следующую деталь: я сказал, что мы аппроксимируем функцию массы вероятности, когда берем гистограмму и делим значения на размер выборки. Истинная функция массы вероятности представляет собой идеализированное распределение вероятностей, что означает, что для этого потребуется бесконечное количество измерений.
Таким образом, когда мы работаем с реалистичными размерами выборки, гистограмма, созданная на основе измеренных данных, дает нам только приближение функции массы вероятности.
Масса вероятности против плотности вероятности
Стоит подчеркнуть, что функция массы вероятности является дискретным эквивалентом функции плотности вероятности (о которой мы говорили в предыдущей статье).
В то время как функция плотности вероятности является непрерывной и предоставляет значения вероятности, когда мы интегрируем функцию в указанном диапазоне, функция массы вероятности дискретизируется и дает нам вероятность, связанную с конкретным значением или интервалом.
Эти две функции передают одну и ту же общую статистическую информацию о переменной или о сигнале, но делают это по-разному.
Обратите внимание на разницу между двумя названиями: вертикальная ось функции массы вероятности указывает массу вероятности, как количественное значение. Вертикальная ось функции плотности вероятности указывает плотность вероятности относительно горизонтальной оси; чтобы определить количественное значение вероятности, мы должны интегрировать эту плотность по горизонтальной оси.
Заключение
Мы рассмотрели функции массы и плотности вероятности, и теперь мы готовы изучить кумулятивную функцию распределения и исследовать вероятности нормального распределения с точки зрения стандартного отклонения. Об этом мы поговорим в следующей статье.
Как визуализировать данные: виды графиков
Визуализация числовых значений позволяет сделать понятными даже сложные наборы данных. Графики и диаграммы привлекают больше аудитории, чем обычный текст или скучные таблицы, и увеличивают вовлеченность читателей. Визуальная информация намного лучше воспринимается и запоминается, что помогает быстро и эффективно донести до аудитории ваши мысли и идеи.
В этой статье разберем основные виды графиков и поговорим о том, каких правил следует придерживаться при визуализации данных.
Типы графиков
Вид диаграммы необходимо выбирать в зависимости от того, какие данные вы хотите визуализировать и с какой целью: чтобы сравнить различные показатели или продемонстрировать, как распределяются данные, скажем, какие значения встречаются чаще, а какие реже.
Также на диаграмме можно наглядно показать структуру чего-либо при помощи данных или проследить взаимосвязь показателей.
Типов диаграмм насчитывается несколько десятков, и в рамках одной статьи описать их все не представляется возможным. Мы рассмотрим наиболее часто используемые виды графиков и разберемся, для отображения каких данных лучше всего подходит каждый их них.
Графики, о которых далее пойдет речь, можно легко создать в таких программах, как Microsoft Word, Excel, PowerPoint и Visio (а также их бесплатных аналогах), приложениях iWork (для iOS и macOS) и онлайн-сервисе Canva.
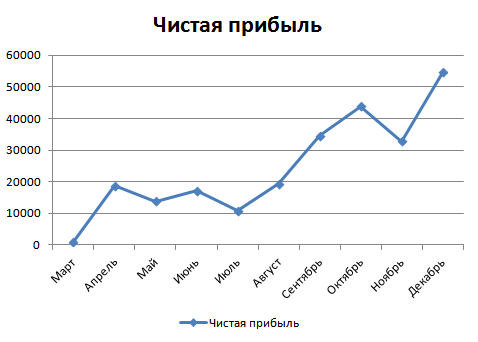
Линейный график
Линейный график (или линейная диаграмма) показывает динамику по одному либо нескольким показателям. Его удобно применять, когда нужно сравнить, как меняются с течением времени разные наборы данных.
Данные на таком графике отображаются в виде точек, которые соединены линиями. Также точки могут быть невидимыми, тогда график представляет собой ломаные линии. Кроме того, существует такая разновидность, как график рассеяния или точечная диаграмма, на котором точки изображаются без линий. Данный тип графика помогает найти взаимосвязь между двумя показателями.
Линейные диаграммы целесообразно применять, если число значений в ряду велико. Они удобны, когда требуется отобразить общую тенденцию развития каких-либо явлений, сравнить темпы роста и т.п.
На такой диаграмме данные категорий равномерно распределены вдоль горизонтальной оси, а все значения отображаются вдоль вертикальной оси. Графики позволяют показать непрерывное изменение данных за определенный период времени, поэтому они прекрасно подходят для представления тенденций изменения данных с равными временными интервалами, такими как месяцы, кварталы или годы.
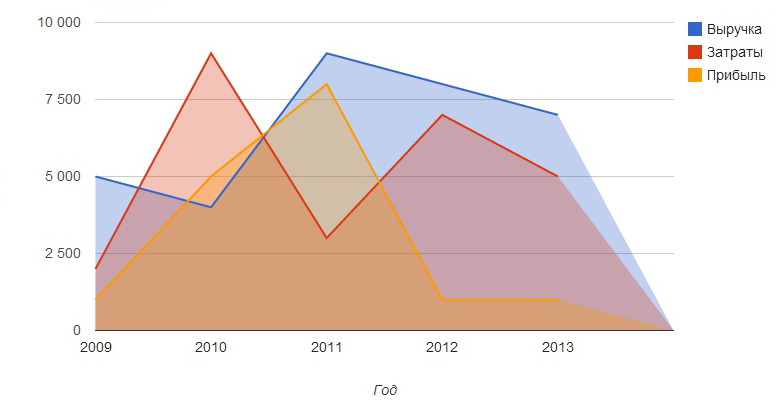
Диаграммы-области
Диаграмма с областями представляет собой линейную диаграмму, в которой область ниже линии заполнена индивидуальным цветом или текстурой. Так же, как и линейные графики, диаграммы-области используются для отображения развития количественных значений в каком-то определенном интервале или за определенный временной период, но отличаются от графиков тем, что позволяют оценить вклад каждого элемента в рассматриваемый процесс.
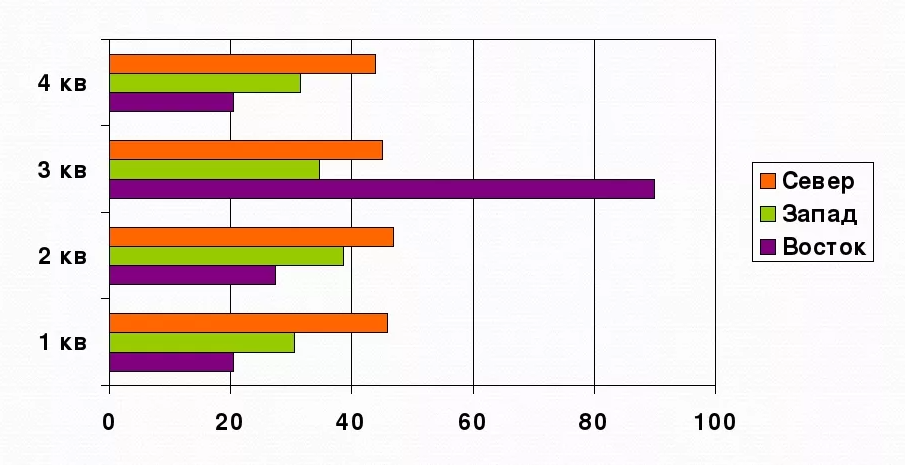
Линейчатые диаграммы
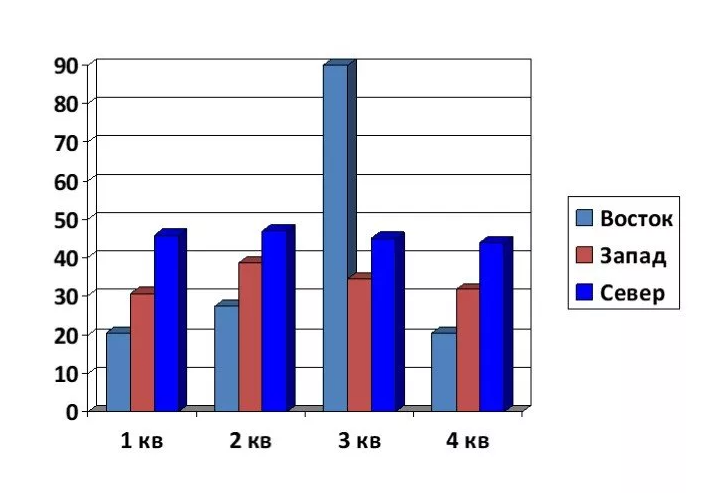
Линейчатые (полосчатые) диаграммы, которые также называют столбчатыми (столбиковыми), являются наиболее часто используемым типом диаграмм.
Они могут применяться для сравнения разных значений в тех случаях, когда важны конкретные числовые показатели. На одной оси столбиковой диаграммы представлены сравниваемые категории, а на другой – шкала числовых значений.
Полосчатые диаграммы позволяют пользователю легко сравнить отдельные значения для разных категорий либо сравнивать изменения значений за какой-то период времени для определенной категории. Статистические показатели в таких диаграммах могут быть представлены как вертикальными, так и горизонтальными столбиками. Для изображения величины параметра используется высота или длина столбика.
Кроме прямоугольников, поверхность таких диаграмм может представлять собой треугольники, трапеции и другие фигуры.
Горизонтальные линейчатые диаграммы обычно используются, когда необходимо сравнить множество различных показателей или визуально обозначить явное превосходство одного из них. Вертикальные столбцы целесообразно использовать для изменения показателей в разные периоды времени, к примеру, ежегодной прибыли компании за несколько лет.
Гистограммы
Гистограмма и столбиковая диаграмма визуально схожи, разница же заключается в том, что гистограмма показывает распределение данных в рамках непрерывного интервала либо конкретного периода времени. На вертикальной оси гистограмм отображается частотность, а на горизонтальной показаны интервалы или временной период.
Гистограммы помогают визуально определить концентрацию значений, а также предельные значения или наличие пробелов либо отклонений.
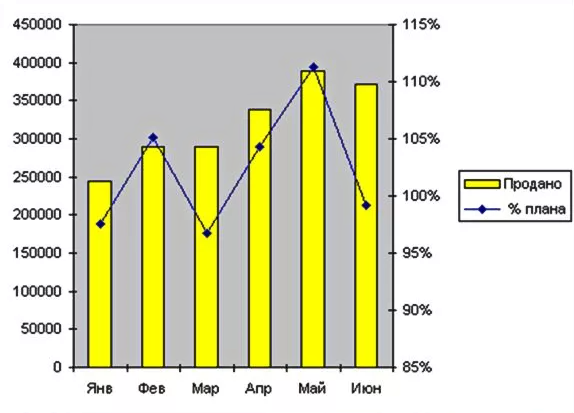
Гистограмма с несколькими осями
Представляет собой сочетание столбиковой диаграммы и линейного графика с двумя осями Y и с одной осью X, на которой показаны категории данных. Такой вариант может понадобиться, когда нужно представить два или более фактора и выявить параллели или сравнения.
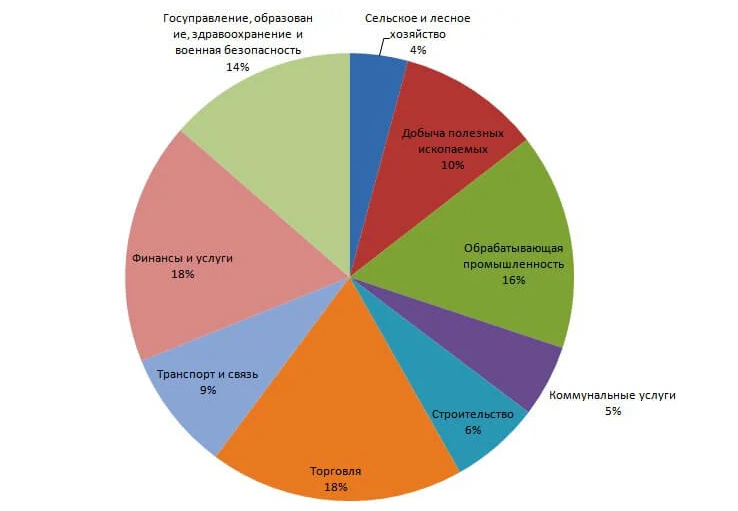
Круговые диаграммы
Круговые (секторные) диаграммы показывают долю каждой величины в общем объеме. Круг представляет всю совокупность данных, а относительная величина каждого отдельного значения изображается в виде сектора круга. Площадь секторов при этом соответствует вкладу этого параметра в сумму значений.
Круговые диаграммы наглядно демонстрируют, какую часть от общего количества составляют отдельные значения. Сектора могут отображаться в общем круге, а также могут быть расположены отдельно на небольшом расстоянии друг от друга.
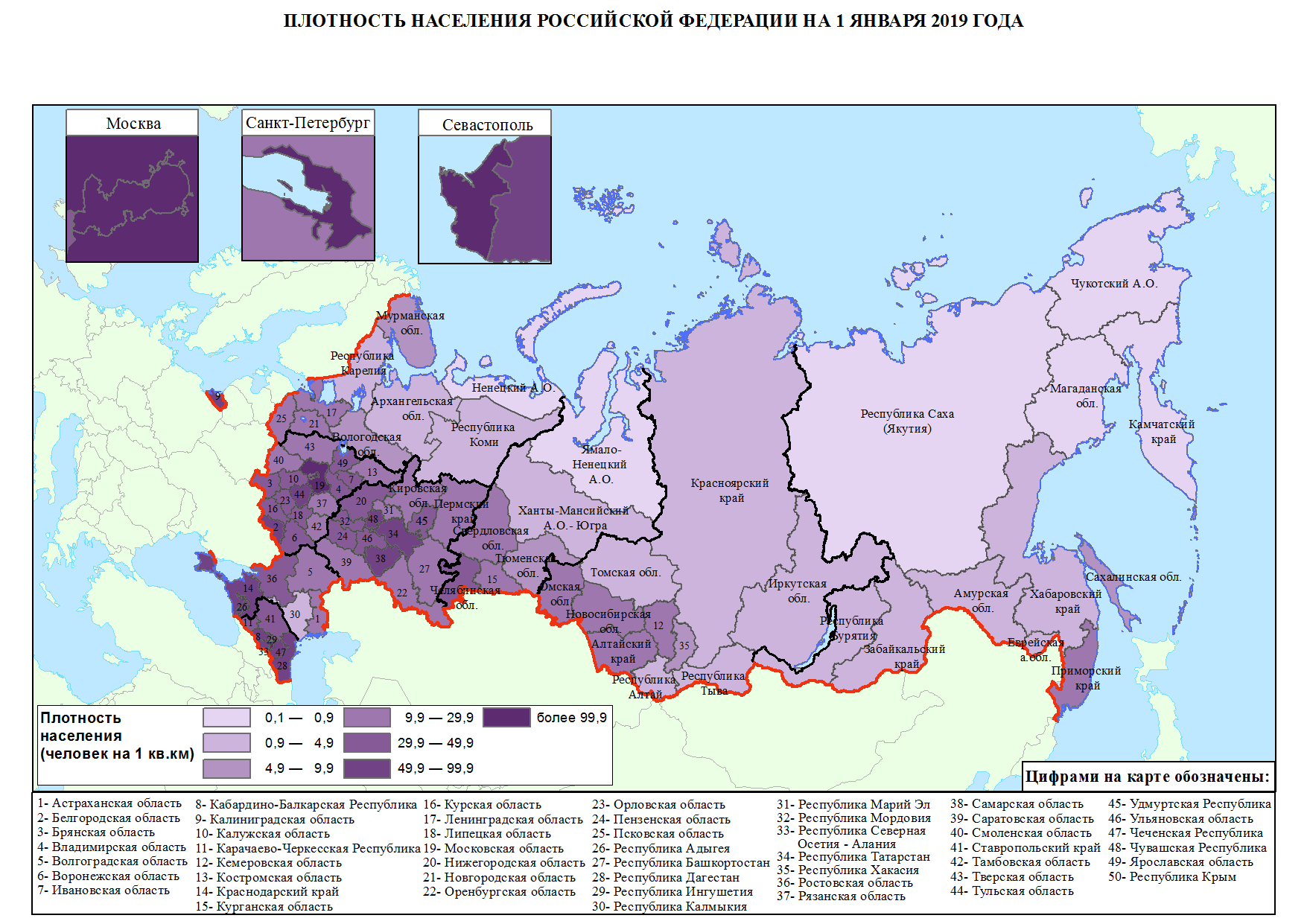
Географические диаграммы
Картодиаграмма являет собой сочетание диаграммы с географической картой или схемой. Ее используют, когда нужно отобразить распределение определенного показателя по регионам, странам, материкам, выделенным разным цветом, оттенками или рисунками в соответствии с переменными данных. На примере диаграммы, приведенной ниже, можно увидеть, что цвет для каждого региона определяется в зависимости от плотности населения.
Если необходимо отобразить на карте данные по дополнительным показателям, это делается с помощью добавления микрографики: круговых диаграмм или столбиков.
Правила визуализации данных
Чтобы графики и диаграммы были понятны читателям, при их построении нужно соблюдать следующие рекомендации:
И еще пара советов: не используйте разные виды графиков и диаграмм для однотипных данных. Читателю требуется время, чтобы привыкнуть к каждому новому виду диаграммы и понять, что обозначает определенная линия или столбик, поэтому всегда выбирайте одинаковые диаграммы для данных одного типа. Кроме того, следует придерживаться одной цветовой гаммы в одном отчете или презентации. Хорошее решение – использование цветов вашего корпоративного стиля.
6 причин, по которым вам следовало бы отказаться от гистограмм
Гистограммам не чужды систематические ошибки. Дело в том, что они достаточно условны и могут привести к неправильным выводам о данных. Если вы хотите визуализировать переменную, лучше выбрать другой график.
Независимо от того, находитесь ли вы на встрече с высшим руководящим составом или со специалистами по обработке данных, в одном вы можете быть уверены: в какой-то момент появится гистограмма.
И нетрудно догадаться почему. Гистограммы весьма интуитивно наглядны: любой поймет их с первого взгляда. Более того, они объективно представляют реальность, не так ли? А вот и нет.
Гистограмма может ввести в заблуждение и привести к ошибочным выводам — даже на простейшем наборе данных!
В этой статье мы на примерах рассмотрим 6 причин, почему, когда дело доходит до визуализации данных, гистограммы точно не является лучшим выбором:
Они слишком сильно зависят от количества интервалов.
Они слишком сильно зависят от максимума и минимума переменной.
Они не дают возможности заметить значимые значения переменной.
Они не позволяют отличить непрерывные переменные от дискретных.
Они делают сравнение распределений сложным.
Их построение затруднено, если в памяти находятся не все данные.
«Ладно, я понял: гистограммы не идеальны. Но есть ли у меня выбор?» Конечно есть!
В конце статьи я порекомендую другой график, называемый CDP, который минует эти недостатки.
Итак, что же не так с гистограммой?
1. Она слишком сильно зависит от количества интервалов.
Чтобы построить гистограмму, вы должны сначала определить количество интервалов, также называемых корзинами (bins). Для этого существует множество различных практических методов (вы можете ознакомиться с их обзором на этой странице). Но насколько критичен этот выбор? Давайте возьмем реальные данные и посмотрим, как меняется гистограмма в зависимости от количества интервалов.
Переменная представляет собой максимальную частоту сердечных сокращений (ударов в минуту), полученную у 303 людей во время некоторой физической активности (данные взяты из набора данных UCI по сердечным заболеваниям: источник).
Как изменяется гистограмма при изменении количества интервалов. [Рисунок автора]
Глядя на верхний левый график (который мы получим по умолчанию в Python и R), у нас сложится впечатление хорошего распределения с одним пиком (модой). Однако если бы мы рассмотрели бы другие варианты гистограммы, мы получили бы совершенно другую картину. Разные гистограммы одних и тех же данных могут привести к противоречивым выводам.
2. Она слишком сильно зависит от максимума и минимума переменной.
Даже после того, как количество интервалов установлено, интервалы зависят от положения минимума и максимума переменной. Достаточно, чтобы один из них немного изменился, и все интервалы также изменятся. Другими словами, гистограммы не являются надежными.
Например, давайте попробуем изменить максимум переменной, не меняя количество интервалов.
Как меняется гистограмма при изменении максимального значения. [Рисунок автора]
Отличается только одно значение, а весь график получается другим. Это нежелательное свойство, потому что нас интересует общее распределение: одно значение не должно так влиять на график!
3. Не дает возможности заметить значимые значения переменной.
Если в общем, то когда переменная содержит некоторые часто повторяющиеся значения, нам конечно нужно об этом знать. Однако гистограммы этому препятствуют, поскольку они основаны на интервалах, а интервалы «скрывают» отдельные значения.
Классическим примером является случай, когда отсутствующим значениям массово присваивается 0. В качестве примера давайте рассмотрим набор данных переменной, состоящий из 10 тысяч значений, 26% из которых — нули.
Те же данные, разная ширина интервала. На левом графике невозможно обнаружить высокую концентрацию нулей. [Рисунок автора]
График слева — это то, что вы получаете по умолчанию в Python. Глядя на него, вы не заметите скопление нулей, и вы даже можете подумать, что эта переменная имеет «плавную» динамику.
График справа получен путем сужения интервалов и дает более четкое представление о реальности. Но дело в том, что как бы вы ни сужали интервалы, вы никогда не будете уверены, содержит ли первый интервал только 0 или какие-то другие значения.
4. Не позволяет отличить непрерывные переменные от дискретных.
Зачастую мы бы хотели знать, является ли числовая переменная непрерывной или дискретной. По гистограмме это практически невозможно сказать.
Возьмем переменную «Возраст» (Age). Вы можете получить Возраст = 49 лет (когда возраст округлен) или Возраст = 49,828884325804246 лет (когда возраст рассчитывается как количество дней с момента рождения, деленное на 365,25). Первая — дискретная переменная, вторая — непрерывная.
Слева непрерывная переменная. Справа дискретная переменная. Однако на верхних графиках они выглядят одинаково. [Рисунок автора]
Тот, что слева, непрерывен, а тот, что справа, дискретен. Однако на верхних графиках (по умолчанию в Python) вы не увидите никакой разницы между ними: они выглядят совершенно одинаково.
5. Сложно сравнивать распределения.
Часто бывает необходимо сравнить одну и ту же переменную в разных кластерах. Например, в отношении данных UCI о сердечных заболеваниях, приведенных выше, мы можем сравнить:
все население (для справки)
люди моложе 50 страдающие сердечными заболеваниями
люди моложе 50 НЕ страдающие сердечными заболеваниями
люди старше 60 лет страдающие сердечными заболеваниями
люди старше 60 и НЕ страдающие сердечными заболеваниями.
Вот что мы получили бы в итоге:
Сравнение гистограмм. [Рисунок автора]
Гистограммы основаны на областях, и, когда мы пытаемся провести сравнение, области в конечном итоге перекрываются, что делает эту задачу практически невыполнимой.
6. Сложно построить, если в памяти находятся не все данные.
Если все ваши данные находятся в Excel, R или Python, построить гистограмму легко: в Excel вам просто нужно кликнуть по иконке гистограммы, в R — выполнить команду hist(x), а в Python — plt.hist(х).
Но предположим, что ваши данные хранятся в базе данных. Вы же не хотите выгружать все данные только для того, чтобы построить гистограмму, верно? По сути, все, что вам нужно, это таблица, содержащая для каждого интервала крайние значения и количество наблюдений. Примерно такая:
| INTERVAL_LEFT | INTERVAL_RIGHT | COUNT |
| 75.0 | 87.0 | 31 |
| 87.0 | 99.0 | 52 |
| 99.0 | 111.0 | 76 |
Но получить ее с помощью SQL-запроса не так просто, как кажется. Например, в Google Big Query код будет выглядеть так:
Немного громоздко, не правда ли?
Альтернатива: график кумулятивного распределения.
График кумулятивного распределения — это график квантилей переменной. Другими словами, каждая точка CDP показывает:
по оси x: исходное значение переменной (как в гистограмме);
по оси y: сколько наблюдений имеют такое же или меньшее значение.
Давайте посмотрим на пример с переменной — максимальной частотой пульса.
График кумулятивного распределения максимальной частоты сердечных сокращений. [Рисунок автора]
Возьмем точку с координатами x = 140 и y = 90 (30%). По горизонтальной оси вы видите значение переменной: 140 ударов сердца в минуту. По вертикальной оси вы видите количество наблюдений, у которых частота сердцебиение равна или ниже 140 (в данном случае 90 человек, что означает 30% выборки). Следовательно, у 30% нашей выборки максимальная частота сердцебиения составляет 140 или менее ударов в минуту.
Какой смысл в графике, показывающем, сколько наблюдений «равно или ниже» заданного уровня? Почему не просто «равно»? Потому что в противном случае результат зависел бы от отдельных значений переменной. И это не сработает, потому что каждое значение имеет очень мало наблюдений (обычно только одно, если переменная непрерывна). Напротив, CDP полагаются на квантили, которые более стабильны, выразительны и легко читаются.
Вдобавок CDP намного полезнее. Если задуматься, вам часто приходится отвечать на такие вопросы, как «у скольких из них от 140 до 160?» Или «у скольких из них больше 180?». Имея перед глазами CDP, вы можете дать немедленный ответ. С гистограммой это было бы невозможно.
CDP решает все проблемы, которые мы видели выше. Фактически, по сравнению с гистограммой:
1. Не требует пользовательского выбора. Для одного набора данных, существует только один возможный CDP.
2. Не страдает от выпадающих значений. Экстремальные значения не влияют на CDP, поскольку квантили не меняются.
3. Позволяет определять значимые значения. Если существует концентрация точек данных на каком-то конкретном значении, это сразу видно, поскольку будет вертикальный сегмент, соответствующий значению.
4. Позволяет с первого взгляда распознать дискретную переменную. Если существует только конкретный набор возможных значений (т.е. переменная дискретна), это сразу видно, поскольку кривая примет форму лестницы.
5. Упрощает сравнение распределений. На одном графике легко сравнить два или более распределения, поскольку это просто кривые, а не области. Кроме того, ось y всегда находится в диапазоне от 0 до 100%, что делает сравнение еще более простым. Для сравнения, это пример, который мы видели выше:
Сравнение распределений в CDP. [Рисунок автора]
6. Его легко построить, даже если у вас нет всех данных в памяти. Все, что вам нужно, это квантили, которые можно легко получить с помощью SQL:
Как построить график кумулятивного распределения в Excel, R, Python
В R это делается в одну строчку:
Спасибо за внимание! Надеюсь, эта статья оказалась для вас полезной.
Я ценю отзывы и конструктивную критику. Если вы хотите поговорить об этой статье или других связанных темах, вы можете написать мне в Linkedin.
Перевод материала подготовлен в рамках онлайн-курса «Machine Learning. Basic«. Всех заинтересованных приглашаем на день открытых дверей курса, где можно будет узнать все подробности об обучении и пообщаться с преподавателем.