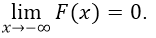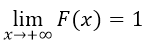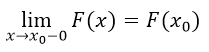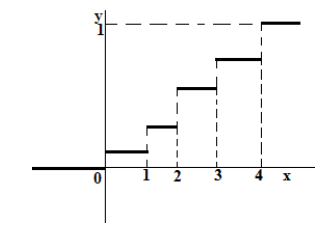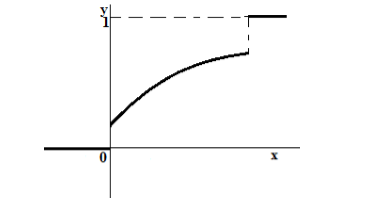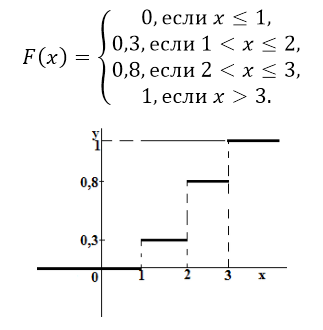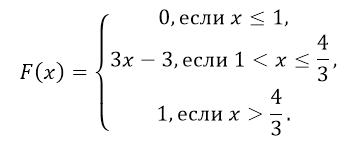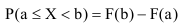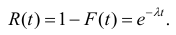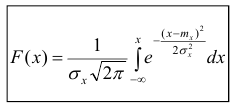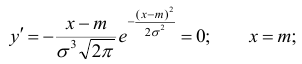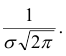Что показывает график функции распределения

Свойства функции распределения, график

Вы будете перенаправлены на Автор24

Свойства функции распределения

Вначале напомним определение функции распределения вероятностей.

Введем свойства функции распределения:

1. Функция распределения является неубывающей функцией.

Используя лемму 1, получим

Докажем теперь, что:

Готовые работы на аналогичную тему

Это свойство очевидно.

Если функция непрерывна во всех точках справа, то$P\left(a\le X\le b\right)=P\left(a

График функции распределения вероятностей

Рисунок 7. Функция распределения смешанной случайной величины

Примеры задач с использованием понятия функции распределения

Найти функцию распределения вероятностей и построить её график.

Решение.

Отсюда получаем следующую функцию распределения вероятностей:

Случайная величина задана следующей функцией распределения:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 20 02 2021

Источник

Содержание:

Законы распределения:

Распределение случайных переменных: Каждая из случайных переменных имеет ряд возможных значений, могущих возникнуть с определенной вероятностью.

Случайные переменные величины могут носить прерывный (дискретный) и непрерывный характер. Возможные значения прерывной случайной переменной отделены друг от друга конечными интервалами. Возможные значения непрерывной случайной переменной не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.

Примерами прерывных случайных переменных могут служить:

Примеры непрерывных случайных переменных:

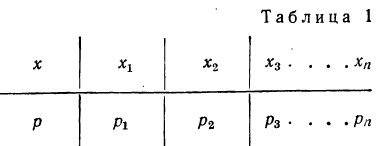
Если перечислить все возможные значения случайной переменной и указать вероятности этих значений, то получится распределение случайной переменной. Распределение случайной переменной указывает на соотношение между отдельными значениями случайной величины и их вероятностями.

Распределение случайной переменной будет задано законом распределения, если точно указать, какой вероятностью обладает каждое значение случайной переменной.

Такая таблица называется также рядом распределения случайной переменной.

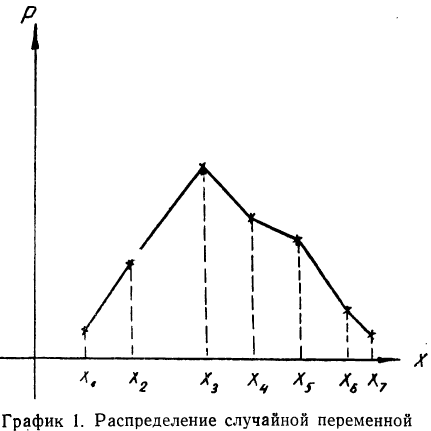
Для наглядности ряд распределения изображают графически, откладывая на прямоугольной системе координат по оси абсцисс возможные значения случайной переменной, а по оси ординат — их вероятности. В результате графического изображения получается многоугольник или полигон распределения (график 1). Многоугольник распределения является одной из форм закона распределения.

Функция распределения

Ряд распределения является исчерпывающей характеристикой прерывной случайной перемен-

Вероятность того, что Х

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Что показывает график функции распределения

1. Формирование представление о случайной величине, дискретных и непрерывных случайных величинах.

2. Знакомство с законом распределения дискретной случайной величины, функцией распределения и плотностью распределения непрерывной случайной величины, числовых характеристиках случайных величин.

1. Виды случайных величин.

2. Закон распределения дискретной случайной величины.

3. Функция распределения вероятностей случайной величины.

4. Плотность распределения вероятностей непрерывной случайной величины.

5. Математическое ожидание.

6. Дисперсия и среднеквадратическое отклонение.

1. Виды случайных величин.

Случайной величиной называется такая величина, которая случайно принимает какое-то значение из множества возможных значений.

По множеству возможных значений различают дискретные и непрерывные случайные величины.

Дискретными называются случайные величины, значениями которых являются только отдельные точки числовой оси. (Число их может быть как конечно, так и бесконечно).

Пример: Число родившихся девочек среди ста новорожденных за последний месяц- это дискретная случайная величина, которая может принимать значения 1,2,3,…

Непрерывными называются случайные величины, которые могут принимать все значения из некоторого числового промежутка.

2. Закон распределения дискретной случайной величины.

Закон распределения дискретной случайной величины— это соответствие между возможными значениями случайной величины и их вероятностями.

Закон распределения можно задать таблично, аналитически, графически.

При задании закона распределения таблично, в первую строку таблицы вносятся возможные значения случайно величины, а во вторую- их вероятности.

Пример: Монету подбросили 3 раза. Запишите закон распределения числа выпадения «герба».

Возможные значения данной случайной величины: 0, 1, 2, 3.

Найдем вероятность того, что «герб» не появится (0 раз).

Найдем вероятность того, что «герб» появится 1 раз.

Найдем вероятность того, что «герб» появится 2 раза.

Найдем вероятность того, что «герб» появится 3 раза.

Тогда закон распределения данной дискретной случайной величины можно представить таблицей:

Для наглядности закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки с координатами (x_i ; p_i), а затем соединяют их отрезками прямых. Полученная фигура называется многоугольником распределения.

Однако, такой способ задания (перечисление всех возможных значений случайной величины и их вероятностей) не подходит для непрерывных случайных величин. Составить перечень их возможных значений невозможно.

3. Функция распределения вероятностей случайной величины.

Дадим новый способ задания любых типов случайных величин. С этой целью введем функцию распределения вероятностей случайной величины.

Функцией распределения случайной величины называют функцию F ( x ), определяющую вероятность того, что случайная величина Х в результате испытания примет значение меньшее х, т.е. F ( x ) P ( X x ).

Геометрически это равенство можно истолковать так: F ( x ) –есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.

Иногда вместо термина «функция распределения» используется термин «интегральная функция».

Свойства функции распределения:

Следствие 1: Вероятность того, что случайная величина примет значение, заключенное в интервале (а; b ), равна приращению функции распределения на этом интервале:

Пример: Случайная величина Х задана функцией распределения:

Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0; 2).

Следствие: Если возможные значения непрерывной случайной величины распределены на всей числовой оси, то справедливы следующие предельные соотношения:

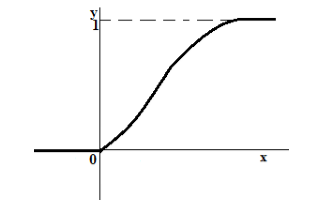
Рассмотренные выше свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.

График расположен в полосе, ограниченной прямыми у=0, у=1 (1 свойство).

4. При возрастании значения х в интервале ( a ; b ), в котором заключены все возможные значения случайной величины, график растет вверх (2 свойство).

5. При ординаты графика равны 0, при ординаты графика равны 1 (3 свойство).

Замечание: График функции распределения дискретной случайной величины имеет ступенчатый вид.

Пример: Дискретная случайная величина Х задана таблицей распределения:

Найдите функцию распределения и постройте ее график.

Итак, функция распределения имеет следующий вид:

4. Плотность распределения вероятностей непрерывной случайной величины.

Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (дифференциальной функцией).

Плотность распределения вероятностей непрерывной случайной величины Х называют функцию f ( x )- первую производную от функции распределения F ( x ).

Пример: Задана плотность вероятностей случайной величины Х.

Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).

Свойства плотности распределения вероятностей:

Свойство 1: Плотность распределения- неотрицательная функция: f ( x ) > 0.

Часто, для того чтобы характеризовать случайную величину используют числа, которые описывают случайную величину суммарно. Такие числа называются числовыми характеристиками случайной величины. К числу важнейших числовых характеристик относятся математическое ожидание и дисперсия.

5. Математическое ожидание.

Математическое ожидание приближенно равно среднему значению случайной величины. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и следовательно стреляет лучше.

Пример: Найдите математическое ожидание, зная закон распределения дискретной случайной величины.

Источник

Что показывает график функции распределения

(F2) cХЭЕУФЧХАФ РТЕДЕМЩ Й ; (F3) ПОБ Ч МАВПК ФПЮЛЕ ОЕРТЕТЩЧОБ УМЕЧБ:

фПЮОП ФБЛ ЦЕ ДПЛБЦЕН ПУФБМШОЩЕ УЧПКУФЧБ.

(F4) ч МАВПК ФПЮЛЕ ТБЪОЙГБ ТБЧОБ :

(F5) дМС МАВПК УМХЮБКОПК ЧЕМЙЮЙОЩ ЙНЕЕФ НЕУФП ТБЧЕОУФЧП:

йЪ УЧПКУФЧ (F4) Й (F5) РПМХЮБЕН УМЕДХАЭЕЕ УЧПКУФЧП.

рПУЛПМШЛХ ЖХОЛГЙС ТБУРТЕДЕМЕОЙС ПДОПЪОБЮОП ПРТЕДЕМСЕФ ТБУРТЕДЕМЕОЙЕ УМХЮБКОПК ЧЕМЙЮЙОЩ ( ЬФХ ЖТБЪХ УФПЙФ ЛБЛ УМЕДХЕФ ПВДХНБФШ!), НПЦОП УЮЙФБФШ ЧПЪНПЦОПУФШ РТЕДУФБЧЙФШ ЖХОЛГЙА ТБУРТЕДЕМЕОЙС ЙОФЕЗТБМПН (14) ПФ ОЕПФТЙГБФЕМШОПК ЖХОЛГЙЙ ПРТЕДЕМЕОЙЕН БВУПМАФОП ОЕРТЕТЩЧОПЗП ТБУРТЕДЕМЕОЙС.

(f3) еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ БВУПМАФОП ОЕРТЕТЩЧОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ЕЈ ЖХОЛГЙС ТБУРТЕДЕМЕОЙС ЧУАДХ ОЕРТЕТЩЧОБ.

ьФПФ ЖБЛФ УМЕДХЕФ ЙЪ УЧПКУФЧБ 7 Й ЙЪ (F4). ъБНЕФЙН, ЮФП (f3) ЕУФШ ФБЛЦЕ УМЕДУФЧЙЕ РТЕДУФБЧМЕОЙС (14) Й ОЕРТЕТЩЧОПУФЙ ЙОФЕЗТБМБ ЛБЛ ЖХОЛГЙЙ ЧЕТИОЕЗП РТЕДЕМБ.

(f4) еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ БВУПМАФОП ОЕРТЕТЩЧОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ЕЈ ЖХОЛГЙС ТБУРТЕДЕМЕОЙС ДЙЖЖЕТЕОГЙТХЕНБ РПЮФЙ ЧУАДХ, Й

пРЙТБСУШ ОБ УЧПКУФЧБ (f4) Й (14), НПЦОП УЖПТНХМЙТПЧБФШ ФБЛПК ЛТЙФЕТЙК БВУПМАФОПК ОЕРТЕТЩЧОПУФЙ ТБУРТЕДЕМЕОЙС: ТБУРТЕДЕМЕОЙЕ У ЖХОЛГЙЕК ТБУРТЕДЕМЕОЙС БВУПМАФОП ОЕРТЕТЩЧОП, ЕУМЙ РТЙ ЧУЕИ ЙНЕЕФ НЕУФП ТБЧЕОУФЧП:

йЪ ПРТЕДЕМЕОЙС БВУПМАФОП ОЕРТЕТЩЧОПЗП ТБУРТЕДЕМЕОЙС Й УЧПКУФЧБ 7 УТБЪХ УМЕДХЕФ УЧПКУФЧП:

(f5) еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ БВУПМАФОП ОЕРТЕТЩЧОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ДМС МАВЩИ ЙНЕАФ НЕУФП ТБЧЕОУФЧБ:

рТЙНЕТПН ФБЛПК ЖХОЛГЙЙ ТБУРТЕДЕМЕОЙС УМХЦЙФ МЕУФОЙГБ лБОФПТБ:

Источник

Содержание:

Непрерывные случайные величины: функция распределения случайной величины:

Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.

Функция распределения непрерывной случайной величины

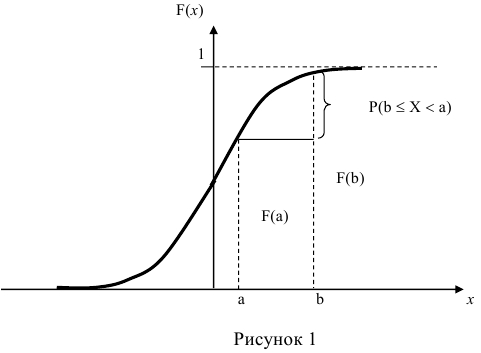
Зная функцию распределения непрерывной случайной величины, задача определения вероятности её попадания на интервал (а; b) может быть решена следующим образом.

По известной функции распределения вероятность попадания непрерывной случайной величины на интервал (а; b) равна приращению функции распределения на этом участке (рис. 1).

Во всех рассмотренных выше случаях случайная величина определялась путём задания значений самой величины и вероятностей этих значений.

Однако такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, её значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.

Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?

Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.

Функция надежности

Определение. Функцией надёжности R(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.

Часто на практике длительность безотказной работы подчиняется показательному закону распределению.

Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.

Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.

Функция надёжности для какого- либо устройства при показательном законе распределения равна:

Данное соотношение называют показательным законом надежности.

Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.

Таким образом, безотказная работа устройства зависит только от интенсивности отказов 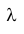и не зависит от безотказной работы устройства в
прошлом.

Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.

Нормальный закон распределения

Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Нормальный закон распределения также называется законом Гаусса.

Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Можно легко показать, что параметры 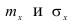входящие в плотность распределения являются соответственно математическим ожиданием и среднеквадратическим отклонением случайной величины X.

Найдём функцию распределения F(x).

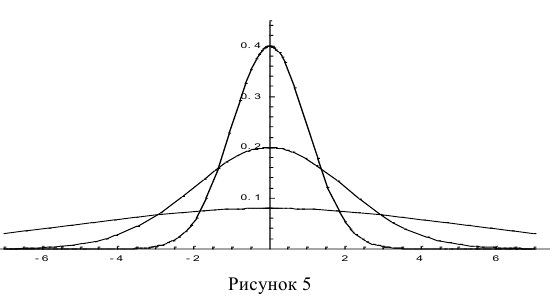
График плотности нормального распределения называется нормальной кривой или кривой Гаусса.

Нормальная кривая обладает следующими свойствами:

1) Функция определена на всей числовой оси.

2) При всех х функция распределения принимает только положительные значения.

3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента л\ значение функции стремится к нулю.

4) Найдём экстремум функции.

Т.к. при 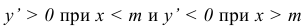, то в точке х = m функция имеет максимум, равный

5) Функция является симметричной относительно прямой x = а, т.к. разность

6) Для нахождения точек перегиба графика найдем вторую производную функции плотности.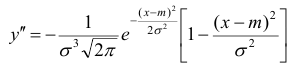

При 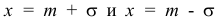вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.

В этих точках значение функции равно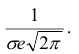
Построим график функции плотности распределения (рис. 5).

Построены графики при м =0 и трёх возможных значениях среднеквадратичного отклонения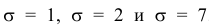. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается.

Если а > 0, то график сместится в положительном направлении, если а

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник