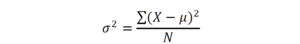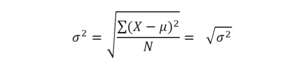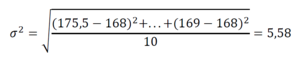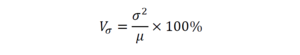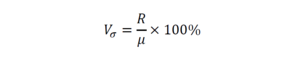Что показывает коэф вариации

Коэффициент вариации (CV)

Коэффициент вариации (coefficient of variation, CV) — это статистическая мера дисперсии (разброса) данных вокруг некоторого среднего значения. Коэффициент вариации представляет собой отношение среднеквадратичного отклонения к среднему значению и является весьма полезной величиной для сравнения степени вариации при переходе от одного ряда данных к другому, даже если их средние значения резко отличаются друг от друга.

Понимание коэффициента вариации

Коэффициент вариации показывает степень изменчивости некоторой выборки данных по отношению к среднему их значению. В финансах данный коэффициент позволяет инвесторам определить, насколько велика волатильность, или риск, по сравнению с величиной ожидаемой прибыли от инвестиций.

Чем меньше значение CV, тем лучший компромисс наблюдается между риском и доходностью. Обратите внимание, что если ожидаемая доходность в знаменателе отрицательна или равна нулю, полученное значение коэффициента может ввести вас в заблуждение.

Коэффициент вариации может быть весьма полезен при использовании соотношения риск/прибыль для выбора объекта инвестиций. Например, инвестор не склонный к риску будет рассматривать активы с исторически низкой степенью волатильности и высокой степенью доходности по отношению к общему рынку (или к отдельной отрасли). И наоборот, инвесторы склонные к риску, будут стремиться инвестировать в активы с исторически высокой степенью волатильности.

Формула CV может использоваться для определения дисперсии между исторической средней ценой и текущими показателями цены акции, товара или облигации.

Обычно данный коэффициент используют в таких целях как:

КЛЮЧЕВЫЕ МОМЕНТЫ

Формула CV

Ниже приведена формула для расчета коэффициента вариации:

Обратите внимание, что если значение ожидаемой доходности в знаменателе формулы коэффициента вариации отрицательна или равна нулю, то результат расчёта по ней нельзя считать корректным.

Коэффициент вариации в Excel и Open Office

Коэффициент вариации можно достаточно легко рассчитать в Excel. Несмотря на то, что в нём нет стандартной функции для расчёта CV, но зато есть функции позволяющие рассчитать стандартное отклонение (СТАНДОТКЛОН) и среднее значение (СРЗНАЧ). Сначала используйте функцию стандартного отклонения, затем вычислите среднее значение, а после этого разделите ячейку, содержащую стандартное отклонение, на ячейку содержащую среднее значение.

В Open Office данный показатель рассчитывается аналогично. Функция стандартного отклонения здесь — STDEV, а функция среднего значения — AVERAGE.

Давайте рассмотрим пример расчёта коэффициента вариации в Open Office. Предположим, что у нас есть три потенциальных объекта для инвестиций — объект А, объект Б и объект В. Прибыль по каждому из этих проектов за последние 6 лет занесена в таблицу представленную ниже:

Давайте рассчитаем значение CV для каждого из этих объектов. Начнём с расчёта стандартных отклонений. Для этого применим к ряду значений прибыли отдельно по каждому объекту функцию STDEV:

Аналогичным образом рассчитаем среднее значение для каждого ряда данных:

Наконец рассчитаем CV. Для этого разделим полученные значения отклонений на средние значения. В результате получим следующую таблицу:

Кликните по картинке для увеличения

Очевидно, что из всех представленных объектов инвестиций предпочтительным будет объект Б имеющий наименьшее значение коэффициента CV.

Пример использования коэффициента вариации для выбора объекта инвестиций

Рассмотрим инвестора не склонного к риску, который хочет инвестировать в биржевой фонд (ETF) состоящий из корзины ценных бумаг отслеживающей индекс широкого рынка. Инвестор выбирает SPDR S&P 500 ETF, Invesco QQQ ETF и iShares Russell 2000 ETF. Затем он анализирует доходность и волатильность выбранных ETF за последние 15 лет и предполагает, что в будущем они могут иметь аналогичную доходность в отношении к своим долгосрочным средним значениям.

Для принятия решения инвестором используется следующая 15-летняя историческая информация:

Исходя из этих данных, инвестор может инвестировать либо в SPDR S&P 500 ETF, либо в iShares Russell 2000 ETF, так как соотношение риска и вознаграждения для них является сравнительно одинаковым. А для Invesco QQQ ETF соотношение риск-доходность, как видите, будет несколько хуже.

Источник

Расчет коэффициента вариации

Понятие коэффициента вариации

В статистике под вариацией величин того или иного показателя в совокупности понимается различие его уровней у тех или иных единиц анализируемого состава в один и тот же период либо момент исследования. В том случае, когда выполняется анализ отличий величин показателя у одного и того же предмета, у одной и той же единицы совокупности в различные периоды или моменты времени, то это будет уже именоваться не вариацией, а колебаниями или изменениями в течении определенного периода.

Размещено на www.rnz.ru

Формула расчета коэффициента вариации

Являясь отношением среднего квадратического отклонения к средней величине, в общем случае анализируемый показатель вычисляется по следующей формуле:

Формула расчета коэффициента вариации

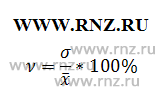
Вычисление рассматриваемого показателя посредством расчета отклонений от средней величины отражает его объективное содержание, но его получение достаточно трудоемко, и для повышения точности выводов требуются расчеты среднего показателя и отклонений без округлений или со значительным количеством цифр после запятой. Поэтому в практических вычислениях делимое может быть вычислено с использованием другой, полученной из общей, формуле вычисления среднего квадратического отклонения в форме разности среднего квадрата элемента и квадрата среднего значения. Таким образом, формула расчета исследуемого показателя, дающая более точный результат, выглядит следующим образом:

Формула расчета точного значения коэффициента вариации

Пример расчета коэффициента вариации

Приведем пример расчета коэффициента вариации цены. Исходные данные для вычисления коэффициента вариации и необходимые промежуточные расчеты приведены в таблице:

Для вычисления используем следующую формулу:

Определим средне значение: х_{среднее} = (17,74 + 13,69 + 16 + 11,87 + 11,21 + 15,09 + 19,49 + 19,97 + 17,03) / 9 = 15,79 руб.

Среднее квадратическое отклонение: σ = √(77,79 / 9) = 2,94.

Коэффициент вариации: ν = 2,94 / 15,79 * 100 = 18,62%.

Интерпретация. Полученное значение исследуемого показателя показывает, что колеблемость цены относительно небольшая и составляет 18,62% среднего уровня. Полученное значение также указывает на однородность исследуемой совокупности, т.к. полученное значение коэффициента вариации менее 33%.

Внимание! Расчет коэффициента вариации по 44 ФЗ имеет свои особенности, поэтому приводим отдельный пример расчета коэффициента вариации по 44 ФЗ

Онлайн калькулятор расчета коэффициента вариации

В заключении приводим небольшой онлайн калькулятор расчета коэффициента вариации онлайн, используя который, Вы можете самостоятельно выполнить расчет указанного показателя онлайн. При заполнении формы калькулятора расчета коэффициента вариации онлайн внимательно соблюдайте размерность полей, что позволит выполнить вычисления онлайн быстро и точно. Дробные величины должны вводиться с точкой, а не с запятой! В форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как работает онлайн калькулятор расчета коэффициента вариации. Для расчета данного показателя по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить расчет». Обратите внимание, что расчет коэффициента вариации онлайн калькулятором осуществляется только по несгруппированным данным.

Онлайн-калькулятор расчета коэффициента вариации:

Источник

Коэффициент вариации в статистике: примеры расчета

Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.

Показатели описательной статистики

Существует несколько показателей, которые использует описательная статистика.

Среднее арифметическое

Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:

Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться. Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического. Если обратиться к росту студентов, то формула будет выглядеть следующим образом:

Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)

Если свести все к строгим математическим терминам, то определение среднего арифметического (обозначается греческой буквой – μ («мю»)) будет звучать так:

Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).

Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.

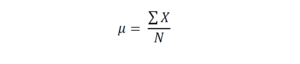
Стандартное отклонение

Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.

На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:

Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:

Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:

Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.

Коэффициент вариации

Среднее квадратичное отклонение хорошо работает с рядами, в которых разброс значений не очень велик (это хорошо прослеживалось на примере роста, где интервал был всего 18 см). Если бы ряд наших измерений был значительнее, а варьирование роста было сильнее, то стандартное отклонение стало непоказательным и нам потребовался бы критерий, который может отразить разброс в относительных единицах (т. е. в процентах, относительно средней величины).

Для этих целей предусмотрены абсолютные и относительные показатели вариации в статистике, характеризующие вариационные масштабы:

Квадратический коэффициент вариации (обозначается как Vσ) – это отношение среднеквадратичного отклонения к среднеарифметическому значению, выраженное в процентах.

Для нашего примера со студентами, определить Vσ несложно — он будет равен 3,18%. Основная закономерность – чем больше будет изменяться значение коэффициента, тем больше разброс вокруг среднего значения и тем менее однородна выборка.

Преимущество коэффициента вариации в том, что он показывает однородность значений (асимметрия) в ряду наших измерений, кроме того, на него не оказывают влияния масштаб и единицы измерения. Эти факторы делают коэффициент вариации особенно популярным в биомедицинских исследованиях. Будет считаться, что эксцесс значения Vσ =33% отделяет однородные выборки от неоднородных.

Если найти в ряду значений роста (первый пример) максимальное и минимальное значения, то получим размах вариации (обозначается как R, иногда ещё называется колеблемостью). В нашем примере – это значение будет равно 18 см. Эта характеристика используется для расчёта коэффициента осцилляции:

Коэффициент осцилляции – показывает как размах вариации будет относиться к среднему арифметическому ряда в процентном отношении.

Расчёты в Microsoft Ecxel 2016

Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:

Наименование показателя	Расчёт в Excel 2016*
Среднее арифметическое	=СРГАРМ(A1:A10)
Дисперсия	=ДИСП.В(A1:A10)
Среднеквадратический показатель	=СТАНДОТКЛОН.В(A1:A10)
Коэффициент вариации	=СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10)
Коэффициент осцилляции	=(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10)

* в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.

Итак, обобщим информацию:

Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила коэффициент вариации, который является мерой однородности данных.

Источник

Коэффициент вариации: для чего нужен, расчет, примеры, упражнения

Содержание:

В коэффициент вариации (CV) выражает стандартное отклонение относительно среднего. То есть он пытается объяснить, насколько велико значение стандартного отклонения по отношению к среднему.

Например, переменный рост четвероклассников имеет коэффициент вариации 12%, что означает, что стандартное отклонение составляет 12% от среднего значения.

Обозначается CV, коэффициент вариации является безразмерным и получается делением стандартного отклонения на среднее значение и умножением на сто.

Чем меньше коэффициент вариации, тем меньше отклонение данных от среднего. Например, в переменной со средним значением 10 и другой со средним значением 25, обе со стандартным отклонением 5, их коэффициенты вариации составляют 50% и 20% соответственно. Конечно, первая переменная более изменчива (дисперсия), чем вторая.

Рекомендуется работать с коэффициентом вариации для переменных, измеряемых в шкале пропорций, то есть шкалах с абсолютным нулем независимо от единицы измерения. Примером может служить переменная расстояния, которая не имеет значения, измеряется она в ярдах или метрах, ноль ярдов или ноль метров означает одно и то же: нулевое расстояние или смещение.

Для чего нужен коэффициент вариации?

Коэффициент вариации служит для:

— Коэффициент вариации часто используется как показатель надежности в научных экспериментах. Говорят, что если коэффициент вариации составляет 30% или больше, результаты эксперимента следует отбросить из-за их низкой надежности.

— Это позволяет предсказать, насколько сгруппированы вокруг среднего значения изучаемой переменной, даже не зная ее распределения. Это очень помогает при оценке ошибок и вычислении размеров выборки.

Предположим, что переменные вес и рост людей измеряются в совокупности. Вес с CV 5% и рост с CV 14%. Если вы хотите взять выборку из этой совокупности, размер выборки должен быть больше для оценок роста, чем для веса, поскольку существует большая вариативность в измерении роста, чем в измерении веса.

Важное наблюдение за полезностью коэффициента вариации заключается в том, что он теряет смысл, когда значение среднего близко к нулю. Среднее значение является делителем вычисления CV, и, следовательно, очень маленькие его значения приводят к тому, что значения CV будут очень большими и, возможно, не поддающимися вычислению.

Как рассчитывается?

Расчет коэффициента вариации относительно прост, достаточно знать среднее арифметическое и стандартное отклонение набора данных, чтобы рассчитать его по формуле:

Если они неизвестны, но данные доступны, можно предварительно рассчитать среднее арифметическое и стандартное отклонение, используя следующие формулы:

Примеры

Пример 1

Были измерены веса в кг группы из 6 человек: 45, 62, 38, 55, 48, 52. Мы хотим знать коэффициент вариации переменной веса.

Он начинается с вычисления среднего арифметического и стандартного отклонения:

Ответ: коэффициент вариации переменного веса 6 человек в выборке составляет 16,64%, при среднем весе 50 кг и стандартном отклонении 8,32 кг.

Пример 2

В отделении неотложной помощи больницы измеряют температуру тела в градусах Цельсия у 5 детей, находящихся на лечении. Результаты 39-е, 38-е, 40-е, 38-е и 40-е. Какой коэффициент вариации переменной температуры?

Он начинается с вычисления среднего арифметического и стандартного отклонения:

Теперь он подставляется в формулу для коэффициента вариации:

Ответ: коэффициент вариации температурной переменной для 5 детей в выборке составляет 2,56%, при средней температуре 39 ° C и стандартном отклонении 1 ° C.

Что касается температуры, то следует проявлять осторожность при обращении с весами, поскольку, будучи переменной, измеряемой в интервальной шкале, она не имеет абсолютного нуля. В рассматриваемом случае, что бы произошло, если бы температуры были преобразованы из градусов Цельсия в градусы Фаренгейта:

Рассчитываются среднее арифметическое и стандартное отклонение:

Теперь он подставляется в формулу для коэффициента вариации:

Ответ: коэффициент вариации температурной переменной у 5 детей в выборке составляет 1,76%, при средней температуре 102,2 ° F и стандартном отклонении 1,80 ° F.

Решенные упражнения

Упражнение 1

Вес в кг 10 сотрудников почтового отделения был измерен: 85, 62, 88, 55, 98, 52, 75, 70, 76, 77. Мы хотим знать коэффициент вариации переменной веса.

Рассчитываются среднее арифметическое и стандартное отклонение:

Теперь он подставляется в формулу для коэффициента вариации:

Ответ: коэффициент вариации переменного веса 10 человек в почтовом отделении составляет 19,74%, при среднем весе 73,80 кг и стандартном отклонении 14,57 кг.

Упражнение 2.

В одном городе измеряется рост 9 465 детей во всех школах первого класса, средний рост составляет 109,90 см со стандартным отклонением 13,59 см. Рассчитайте коэффициент вариации.

Ответ: коэффициент вариации переменного роста первоклассников города составляет 12,37%.

Упражнение 3.

Смотритель парка подозревает, что популяции черных и белых кроликов в его парке не имеют одинаковой изменчивости в размерах. Чтобы продемонстрировать это, он взял образцы по 25 кроликов из каждой популяции и получил следующие результаты:

— Белые кролики: средний вес 7,65 кг и стандартное отклонение 2,55 кг.
-Черные кролики: средний вес 6,00 кг и стандартное отклонение 2,43 кг.

Смотритель парка прав? Ответ на гипотезу смотрителя парка можно получить с помощью коэффициента вариации:

Ответ: коэффициент вариации веса черных кроликов почти на 7% больше, чем у белых кроликов, поэтому можно сказать, что смотритель парка прав в своем подозрении, что вариабельность веса двух популяций кроликов не равны.

Ссылки

Эффект кросса: что это такое и как влияет на восприятие

Источник

Тема 9 Показатели вариации

Показатели вариации в анализе взаимосвязей

Для измерения степени колеблемости отдельных значений признака относительно средней исчисляют основные показатели вариации.

Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для полного анализа изучаемого процесса или явления. Иногда совершенно непохожие по своему внутреннему строению совокупности могут иметь равные средние величины. Поэтому для более детального изучения того или иного явления необходимо учитывать разброс или вариацию значений отдельных единиц совокупности. Измерение вариации признаков имеет как теоретическое, так и практическое значение.

Так, например, для выявления наиболее стабильно работающего коллектива или предприятия наравне с другими показателями рассчитывают и основные показатели вариации. Эти показатели дают возможность количественно определить размеры устойчивости производительности труда, уровня квалификации, цен на основные виды выпускаемой продукции и т.п. Измерение размеров вариации такого показателя, как «выполнение работ в срок» имеет важное значение для принятия решений заказчиками и инвесторами, т.к. ситуация, в которой присутствует изменчивость признака, часто содержит риск. Осо­бое значение показатели вариации приобретают в анализе рынка ценных бумаг, где мера колеблемости отождествляется с мерой рискованности вложения денежных средств.

Основными показателями, характеризующими вариацию, являются:

1) Размах вариации

2) Среднее линейное отклонение исчисляют для того, чтобы дать обобщающую характеристику распределению отклонений:

где –абсолютные значения отклонений отдельных вариантов xi от средней арифметической ; fi – частота.

3. Дисперсия – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической:

4. Среднее квадратическое отклонение – корень квадратный из дисперсии:

5. Коэффициент вариации – используется для сравнительной оценки вариации, а также для характеристики однородности совокупности:

Пример. Для иллюстрации расчетов воспользуемся данными нижеприведенной табл. 9.1:

Таблица 9.1 ‑ Данные о продаже основных марок холодильников:

Рассчитаем размах вариации.

R= 1200-460=740$

Пример вычисления размаха вариации

Размах вариации служит незаменимой мерой разброса экстремальных значений признака. Кроме характеристики границ разброса признака, размах вариации может быть использован для выявления ошибок. При наличии очень больших (или очень малых) ошибочно записанных значений признака размах вариации сразу резко возрастает, что требует проверки и корректировки исходных данных.

Недостатком данного показателя является то, что он оценивает только границы варьирующего признака и не отражает его колеблемость внутри этих границ. Вследствие этого размах вариации может неправильно характеризовать общую колеблемость признака.

Этого недостатка лишен другой показатель – дисперсия, рассчитываемый как средний квадрат отклонений значений признака от их средней величины.

Между индиви­дуальными отклонениями от средней и колеблемостью признака существует прямая зави­симость: чем сильнее колеблемость признака, тем больше отклонения его значений от средней величины и менее устойчив изучаемый показатель.

Как и средняя величина этот показатель может быть рассчитан в двух формах: взвешенной и невзвешенной

По приведенным выше данным определим средневзвешенную цену холодильника:

Далее рассчитаем дисперсию:

. Следует отметить, что дисперсия еще не дает представления об однородности со­вокупности, и этому показателю трудно дать экономическую интерпретацию, т.к. он рас­считан в квадратных единицах. Поэтому следующим шагом в исследовании однородности совокупности является расчет среднего квадратического отклонения, показывающего, на­сколько в среднем отклоняются конкретные варианты признака от его среднего значения. Оно определяется как квадратный корень из дисперсии и имеет ту же размерность что и изучаемый признак. .

Рассчитаем среднее квадратическое отклонение

Рассмотренные показатели позволяют получить абсолютное значение вариации признака. Однако для сравнения разных совокупностей с точки зрения устойчивости ка­кого-либо одного признака или для определения однородности совокупности рассчиты­вают относительные показатели.

Эти показатели вычисляются как отношение размаха вариации, среднего линейно­го отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего эти показатели выражаются в процентах.

Определим значение показателя вариации по вышеприведенным данным таблицы

Совокупность считается однородной, если V не превышает 33%.

Если V 25% – вариация сильная.

Вывод: Рассчитанная величина свидетельствует о неоднородности цен на холодильники, т.к. однородной совокупность считается, если коэффициент вариации меньше 33% (для распределений близких к нормальному).

!! Следует отметить, что коэффициент вариации может быть более 100%, что, в част­ности, может быть при наличии значений сильно отличающихся от средней величины. Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине.

Изучая вариацию интересующего нас признака в пределах исследуемой совокупно­сти и опираясь на общую среднюю в расчетах, трудно оценить степень воздействия на него какого-либо отдельного признака.

При проведении такого анализа исходная совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками – факторным (оказывающим влияние на взаимосвязанный с ним признак) и результативным (подвер­женным влиянию).

Для выявления взаимосвязи исходная совокупность делится по факторному признаку на группы. Выводы о степени взаимосвязи базируются на анализе вариации резуль­тативного признака. Если статистическая совокупность разбита на группы по какому-либо признаку, то для оценки влияния различных факторов, определяющих вариацию индиви­дуальных значений признака, используют правило сложения дисперсий.

Общая дисперсия представляет собой сумму средней из виутригрупповой и меж­групповой и дисперсий:

Общая дисперсия характеризует вариацию признака по всей совокупности как ре­зультат влияния всех факторов, определяющих индивидуальные различия единиц сово­купности.

Межгрупповая дисперсия характеризует вариацию, обусловленную влиянием фактора, положенного в основу группировки.

Средняя из внутригрупповых дисперсий отражает ту часть вариации результа­тивного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка. Другими словами внутригрупповая дисперсия отражает случайную вариацию. Внутригрупповая дисперсия рас­считывается отдельно по каждой j-ой группе.

Для всех групп в целом вычисляется средняя из внутригрупповых дисперсий, взвешенных на частоты соответствующих групп по формуле:

Взаимосвязь между тремя видами дисперсий получила название правила сложения дисперсий. Таким образом, зная два вида дисперсий всегда можно определить третий:

Из этого равенства следует, что общая дисперсия, как правило, будет больше средней из групповых дисперсий. Это обусловлено тем, что при расчленении об­щей совокупности единиц на части по какому-либо признаку образуются более или менее однородные группы, в результате чего сокращается колеблемость признаков в пределах каждой группы. Это приводит к тому, что средняя из групповых дисперсий оказывается меньше дисперсии признака по всей совокупности единиц, причем разница между этими показателями будет тем больше, чем однороднее получаются группы в результате расчле­нения общей совокупности.

Теснота связи между факторным и результативным признаками оценивается на ос­нове эмпирического корреляционного отношения:

Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.

Пример. На следующем условном примере исследуем зависимость объема выполненных ра­бот от формы собственности проектно-изыскательских организаций.

Таблица 9.2. Выполнение работ проектно-изыскательскими организациями разной формы собственности

Объем выполненных работ

Форма собственности	Количество предприятий	Итого
Государственная	4	10,30,20,40	100
Негосударственная	6	20, 40, 60, 20, 50, 50	240
Итого	10	340

1) Определим средний объем работ для предприятий двух форм собственности.

2) Определим средний объем работ для каждой формы собственности.

3) Рассчитаем общую и внутригрупповые (т.е. для каждой группы) дисперсии.

4) Определим среднюю из внутригрупповых и межгрупповую дисперсию. Для этого полученные ранее данные заносятся в таблицу расчета.

Таблица 9.3. – Вспомогательная таблица

Государственная425125Негосударственная640233Итого10

Пример. Средняя из внутригрупповых дисперсий

Пример. Межгрупповая дисперсия

На последнем этапе решения задачи необходимо проверить тождество, отражающее закон сложения дисперсий:

Проверка закона сложения дисперсий: 54,0+189,8=243,8

Вывод: Таким образом, можно сделать вывод о том, что объем работ, выполненных проектно-изыскательскими организациями на 22% [(54,0/243,8) х 100%] зависит от фак­тора, положенного в основание группировки, т.е. от формы собственности, а на 78% [(189,8/243,8)х100%)] ‑ от прочих факторов.

Вывод о том, что объем выполненных работ в гораздо большей степени зависит от каких-либо других факторов, чем от формы собственности предприятий подтверждается и величиной эмпирического корреляционного отношения:

Вывод: Величина этого показателя свидетельствует о том, что зависимость объема работ от формы собственности предприятия невелика

Контрольные задания

Вычислить: а) размах вариации; б)среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; относительные показатели вариации возраста студентов.

2. По данным статистических ежегодников постройте таблицу с рядом показателей и определите показатели вариации: а) размах; б) среднее линейное отклонение; в) среднее квадратическое отклонение; г) коэффициент вариации. Оцените количественную однородность совокупности.

Источник