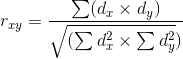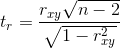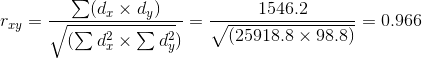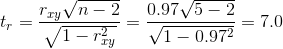Что показывает коэффициент корреляции тест
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
КРИТЕРИЙ КОРРЕЛЯЦИИ ПИРСОНА
– это метод параметрической статистики, позволяющий определить наличие или отсутствие линейной связи между двумя количественными показателями, а также оценить ее тесноту и статистическую значимость. Другими словами, критерий корреляции Пирсона позволяет определить, изменяется ли (возрастает или уменьшается) один показатель в ответ на изменения другого? В статистических расчетах и выводах коэффициент корреляции обычно обозначается как rxy или Rxy.
1. История разработки критерия корреляции
Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.
2. Для чего используется критерий корреляции Пирсона?
Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.
Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.
3. Условия и ограничения применения критерия хи-квадрат Пирсона
Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.
В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.
Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов.
4. Как рассчитать коэффициента корреляции Пирсона?
Расчет коэффициента корреляции Пирсона производится по следующей формуле:
5. Как интерпретировать значение коэффициента корреляции Пирсона?
Более точную оценку силы корреляционной связи можно получить, если воспользоваться таблицей Чеддока:
| Абсолютное значение rxy | Теснота (сила) корреляционной связи |
| менее 0.3 | слабая |
| от 0.3 до 0.5 | умеренная |
| от 0.5 до 0.7 | заметная |
| от 0.7 до 0.9 | высокая |
| более 0.9 | весьма высокая |
Оценка статистической значимости коэффициента корреляции rxy осуществляется при помощи t-критерия, рассчитываемого по следующей формуле:
Полученное значение tr сравнивается с критическим значением при определенном уровне значимости и числе степеней свободы n-2. Если tr превышает tкрит, то делается вывод о статистической значимости выявленной корреляционной связи.
6. Пример расчета коэффициента корреляции Пирсона
Целью исследования явилось выявление, определение тесноты и статистической значимости корреляционной связи между двумя количественными показателями: уровнем тестостерона в крови (X) и процентом мышечной массы в теле (Y). Исходные данные для выборки, состоящей из 5 исследуемых (n = 5), сведены в таблице:
Σ(X) = 951 + 874 + 957 + 1084 + 903 = 4769
Σ(Y) = 83 + 76 + 84 + 89 + 79 = 441
Mx = Σ(X) / n = 4769 / 5 = 953.8
My = Σ(Y) / n = 441 / 5 = 82.2
Ответы на тесты по эконометрике
Q=………..min соответствует методу наименьших квадратов
Автокорреляция — это корреляционная зависимость уровней ряда от предыдущих значений.
Автокорреляция имеется когда каждое следующее значение остатков
Аддитивная модель временного ряда имеет вид: Y=T+S+E
Атрибутивная переменная может употребляться, когда: независимая переменная качественна;
В каких пределах изменяется коэффициент детерминанта: от 0 до 1.
В каком случае модель считается адекватной Fрасч>Fтабл
В каком случае рекомендуется применять для моделирования показателей с увелич. ростом параболу если относительная величина…неограниченно
В результате автокорреляции имеем неэффективные оценки параметров
В хорошо подобранной модели остатки должны иметь нормальный закон
В эконометрическом анализе Xj рассматриваются как случайные величины
Величина доверительного интервала позволяет установить предположение о том, что: интервал содержит оценку параметра неизвестного.
Величина рассчитанная по формуле r=…является оценкой парного коэф. Корреляции
Внутренне нелинейная регрессия — это истинно нелинейная регрессия, которая не может быть приведена к линейной регрессии преобразованием переменных и введением новых переменных.
Временной ряд — это последовательность значений признака (результативного переменного), принимаемых в течение последовательных моментов времени или периодов.
Выберете авторегрессионную модель Уt=a+b0x1+Ɣyt-1+ƹt
Выберете модель с лагами Уt= a+b0x1…….(самая длинная формула)
Выборочное значение Rxy не > 1, |R| : rxy=Ca(x;y) разделить на корень Var(x)*Var(y): коэффициент. корреляции
Какая функция используется при моделировании моделей с постоянным ростом степенная
Какие точки исключаются из временного ряда процедурой сглаживания и в начале, и в конце.
Какое из уравнений регрессии является степенным y=a˳aͯ¹a
Классический метод к оцениванию параметров регрессии основан на: – метод наименьших квадратов (МНК)
Количество степеней свободы для t статистики при проверки значимости параметров регрессии из 35 наблюдений и 3 независимых переменных 31;
Количество степеней свободы знаменателя F-статистики в регрессии из 50 наблюдений и 4 независимых переменных: 45
Компоненты вектора Ei имеют нормальный закон
Корреляция — стохастическая зависимость, являющаяся обобщением строго детерминированной функциональной зависимости посредством включения вероятностной (случайной) компоненты.
Коэффициент автокорреляции: характеризует тесноту линейной связи текущего и предстоящего уровней ряда
Коэффициент детерминации — показатель тесноты стохастической связи в общем случае нелинейной регрессии
Коэффициент детерминации – это величина, которая характеризует связь между зависимыми и независимыми переменными.
Коэффициент детерминации – это квадрат множественного коэффициента корреляции
Коэффициент детерминации – это: величина, которая характеризует связь между независимой и зависимой (зависящей) переменными;
Коэффициент детерминации R показывает долю вариаций зависимой переменной y, объяснимую влиянием факторов, включаемых в модель.
Коэффициент детерминации изменяется в пределах: – от 0 до 1
Коэффициент доверия — это коэффициент, который связывает линейной зависимостью предельную и среднюю ошибки, выясняет смысл предельной ошибки, характеризующей точность оценки, и является аргументом распределения (чаще всего, интеграла вероятностей). Именно эта вероятность и есть степень надежности оценки.
Коэффициент доверия (нормированное отклонение) — результат деления отклонения от среднего на стандартное отклонение, содержательно характеризует степень надежности (уверенности) полученной оценки.
Коэффициент корелляции Rxy используется для определения полноты связи X и Y.
Коэффициент корелляции равный 0 означает, что: –отсутствует линейная связь.
Коэффициент корреляции используется для: определения тесноты связи между случайными величинами X и Y;
Коэффициент корреляции рассчитывается для измерения степени линейной взаимосвязи между двумя случайными переменными.
Коэффициент линейной корреляции — показатель тесноты стохастической связи между фактором и результатом в случае линейной регрессии.
Коэффициент регрессии — коэффициент при факторной переменной в модели линейной регрессии.
Коэффициент регрессии b показывает: на сколько единиц увеличивается y, если x увеличивается на 1.
Коэффициент эластичности измеряется в: неизмеримая величина.
Критерий Дарвина-Чотсона применяется для: – отбора факторов в модель; или – определения автокорреляции в остатках
Критерий Стьюдента — проверка значимости отдельных коэффициентов регрессии и значимости коэффициента корреляции.
Критерий Фишера показывает статистическую значимость модели в целом на основе совокупной достоверности всех ее коэффициентов;
Лаговые переменные это значение зависимых переменных за предшествующий период времени
Модель в целом статистически значима, если Fрасч > Fтабл.
Модель идентифицирована, если: – число параметров структурной модели равно числу параметров приведён. формы модели.
Модель неидентифицирована, если: – число приведён. коэф . больше числа структурных коэф.
Модель сверхидентифицирована, если: число приведён. коэф. меньше числа структурных коэф
Мультипликативная модель временного ряда имеет вид: – Y=T*S*E
Мультипликативная модель временного ряда строится, если: амплитуда сезонных колебаний возрастает или уменьшается
На основе поквартальных данных…значения 7-1 квартал, 9-2квартал и 11-3квартал …-5
Неправильный выбор функциональной формы или объясняющих переменных называется ошибками спецификации
Несмещённость оценки параметра регрессии, полученной по МНК, означает: – что она характеризуется наименьшей дисперсией.
Одной из проблем которая может возникнуть в многофакторной регрессии и никогда не бывает в парной регрессии, является корреляция между независимыми переменными
От чего зависит количество точек, исключаемых из временного ряда в результате сглаживания: от применяемого метода сглаживания.
Отметьте основные виды ошибок спецификации: отбрасывание значимой переменной; добавление незначимой переменной;
Оценки коэффициентов парной регрессии является несмещённым, если: математические ожидания остатков =0.
Оценки параметров парной линейной регрессии находятся по формуле b= Cov(x;y)/Var(x);a=y¯ bx¯
Оценки параметров регрессии являются несмещенными, если Математическое ожидание остатков равно 0
Оценки парной регрессии явл. эффективными, если: оценка обладают наименьшей дисперсией по сравнению с другими оценками
При наличии гетероскедастичности следует применять: – обобщённый МНК
При проверке значимости одновременно всех параметров регрессии используется: F-тест.
Применим ли метод наименьших квадратов для расчетов параметров показательной зависимости применим после ее приведения
Применим ли метод наименьших квадратов(МНК) для расчёта параметров нелинейных моделей? применим после её специального приведения к линейному виду
С помощью какого критерия оценивается значимость коэффициента регрессии T стьюдента
С увеличением числа объясняющих переменных скоррестированный коэффициент детерминации: – увеличивается.
Связь между индексом множественной детерминации R² и скорректированным индексом множественной детерминации Ȓ² есть
Скорректиров. коэф. детерминации: – больше обычного коэф. детерминации
Стандартизованный коэффициент уравнения регрессии Ƀk показывает на сколько % изменится результирующий показатель у при изменении хi на 1%при неизмененном среднем уровне других факторов
Стандартный коэффициент уравнения регрессии: показывает на сколько 1 изменится y при изменении фактора xk на 1 при сохранении др.
Суть коэф. детерминации r 2 xy состоит в следующем: – характеризует долю дисперсии результативного признака y объясняем. регресс., в общей дисперсии результативного признака.
Табличные значения Фишера (F) зависят от доверительной вероятности и от числа включённых факторов и от длины исходного ряда (от доверительной вероятности p и числа степеней свободы дисперсий f1 и f2)..
Уравнение в котором H число эндогенных переменных, D число отсутствующих экзогенных переменных, идентифицируемо если D+1=H
Уравнение в котором H число эндогенных переменных, D число отсутствующих экзогенных переменных, НЕидентифицируемо если D+1 H
Уравнение идентифицировано, если: – D+1=H
Уравнение неидентифицировано, если: – D+1 H
Фиктивные переменные – это: атрибутивные признаки (например, как профессия, пол, образование), которым придали цифровые метки;
Формула t= rxy….используется для проверки существенности коэффициента корреляции
Частный F-критерий: – оценивает значимость уравнения регрессии в целом
Число степеней свободы для факторной суммы квадратов в линейной модели множественной регрессии равно: m;
Что показывает коэффициент наклона – на сколько единиц изменится у, если х изменился на единицу,
Что показывает коэффициент. абсолютного роста на сколько единиц изменится у, если х изменился на единицу
Экзогенная переменная – это независимая переменная или фактор-Х.
Экзогенные переменные — это переменные, которые определяются вне системы и являются независимыми
Экзогенные переменные – это предопределенные переменные, влияющие на зависимые переменные (Эндогенные переменные), но не зависящие от них, обозначаются через х
Эластичность измеряется единица измерения фактора…показателя
Эндогенные переменные – это: зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через у
Определения
T-отношение (t-критерий) — отношение оценки коэффициента, полученной с помощью МНК, к величине стандартной ошибки оцениваемой величины.
Аддитивная модель временного ряда – это модель, в которой временной ряд представлен как сумма перечисленных компонент.
Критерий Фишера — способ статистической проверки значимости уравнения регрессии, при котором расчетное (фактическое) значение F-отношения сравнивается с его критическим (теоретическим) значением.
Линейная регрессия — это связь (регрессия), которая представлена уравнением прямой линии и выражает простейшую линейную зависимость.
Метод инструментальных переменных — это разновидность МНК. Используется для оценки параметров моделей, описываемых несколькими уравнениями. Главное свойство — частичная замена непригодной объясняющей переменной на такую переменную, которая некоррелированна со случайным членом. Эта замещающая переменная называется инструментальной и приводит к получению состоятельных оценок параметров.
Метод наименьших квадратов (МНК) — способ приближенного нахождения (оценивания) неизвестных коэффициентов (параметров) регрессии. Этот метод основан на требовании минимизации суммы квадратов отклонений значений результата, рассчитанных по уравнению регрессии, и истинных (наблюденных) значений результата.
Множественная линейная регрессия — это множественная регрессия, представляющая линейную связь по каждому фактору.
Множественная регрессия — регрессия с двумя и более факторными переменными.
Модель идентифицируемая — модель, в которой все структурные коэффициенты однозначно определяются по коэффициентам приведенной формы модели.
Модель рекурсивных уравнений — модель, которая содержит зависимые переменные (результативные) одних уравнений в роли фактора, оказываясь в правой части других уравнений.
Мультипликативная модель – модель, в которой временной ряд представлен как произведение перечисленных компонент.
Несмещенная оценка — оценка, среднее которой равно самой оцениваемой величине.
Нулевая гипотеза — предположение о том, что результат не зависит от фактора (коэффициент регрессии равен нулю).
Обобщенный метод наименьших квадратов (ОМНК) — метод, который не требует постоянства дисперсии (гомоскедастичности) остатков, но предполагает пропорциональность остатков общему множителю (дисперсии). Таким образом, это взвешенный МНК.
Объясненная дисперсия — показатель вариации результата, обусловленной регрессией.
Объясняемая (результативная) переменная — переменная, которая статистически зависит от факторной переменной, или объясняющей (регрессора).
Остаточная дисперсия — необъясненная дисперсия, которая показывает вариацию результата под влиянием всех прочих факторов, неучтенных регрессией.
Предопределенные переменные — это экзогенные переменные системы и лаговые эндогенные переменные системы.
Приведенная форма системы — форма, которая, в отличие от структурной, уже содержит одни только линейно зависящие от экзогенных переменных эндогенные переменные. Внешне ничем не отличается от системы независимых уравнений.
Расчетное значение F-отношения — значение, которое получают делением объясненной дисперсии на 1 степень свободы на остаточную дисперсию на 1 степень свободы.
Регрессия (зависимость) — это усредненная (сглаженная), т.е. свободная от случайных мелкомасштабных колебаний (флуктуаций), квазидетерминированная связь между объясняемой переменной (переменными) и объясняющей переменной (переменными). Эта связь выражается формулами, которые характеризуют функциональную зависимость и не содержат явно стохастических (случайных) переменных, которые свое влияние теперь оказывают как результирующее воздействие, принимающее вид чисто функциональной зависимости.
Регрессор (объясняющая переменная, факторная переменная) — это независимая переменная, статистически связанная с результирующей переменной. Характер этой связи и влияние изменения (вариации) регрессора на результат исследуются в эконометрике.
Система взаимосвязанных уравнений — это система одновременных или взаимозависимых уравнений. В ней одни и те же переменные выступают одновременно как зависимые в одних уравнениях и в то же время независимые в других. Это структурная форма системы уравнений. К ней неприменим МНК.
Система внешне не связанных между собой уравнений — система, которая характеризуется наличием одних только корреляций между остатками (ошибками) в разных уравнениях системы.
Случайный остаток (отклонение) — это чисто случайный процесс в виде мелкомасштабных колебаний, не содержащий уже детерминированной компоненты, которая имеется в регрессии.
Состоятельные оценки — оценки, которые позволяют эффективно применять доверительные интервалы, когда вероятность получения оценки на заданном расстоянии от истинного значения параметра становится близка к 1, а точность самих оценок увеличивается с ростом объема выборки.
Спецификация модели — определение существенных факторов и выявление мультиколлинеарности.
Стандартная ошибка — среднеквадратичное (стандартное) отклонение. Оно связано со средней ошибкой и коэффициентом доверия.
Степени свободы — это величины, характеризующие число независимых параметров и необходимые для нахождения по таблицам распределений их критических значений.
Тренд — основная тенденция развития, плавная устойчивая закономерность изменения уровней ряда.
Уровень значимости — величина, показывающая, какова вероятность ошибочного вывода при проверке статистической гипотезы по статистическому критерию.
Фиктивные переменные — это переменные, которые отражают сезонные компоненты ряда для какого-либо одного периода.
Эконометрическая модель — это уравнение или система уравнений, особым образом представляющие зависимость (зависимости) между результатом и факторами. В основе эконометрической модели лежит разбиение сложной и малопонятной зависимости между результатом и факторами на сумму двух следующих компонентов: регрессию (регрессионная компонента) и случайный (флуктуационный) остаток. Другой класс эконометрических моделей образует временные ряды.
Эффективность оценки — это свойство оценки обладать наименьшей дисперсией из всех возможных.
Линейный коэффициент корреляции Пирсона
Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.
Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.
Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.
Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.
При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.
Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.
Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?
Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.
Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.
Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.
Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.
Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.
Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.к. является относительным показателем и не имеет единиц измерения.
Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r 2 = 0,01 или 1%, при r = 0,5 r 2 = 0,25 или 25%.
Выборочный коэффициент корреляции
Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.
Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.
В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:
Распределение z для тех же r имеет следующий вид.
Намного ближе к нормальному. Стандартная ошибка z равна:
Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.
Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:
Это была теоретическая часть. Переходим к практике расчетов.
Как посчитать коэффициент корреляции в Excel
Корреляционный анализ в Excel лучше начинать с визуализации.
На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.
Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.
Расчет доверительного интервала для коэффициента корреляции в Excel
В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:
— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.
Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.
Стандартная ошибка z легко подсчитывается с помощью формулы.
Используя функцию НОРМ.СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.
Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.
Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.
Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.
Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.
Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.
Несколько важных замечаний
1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).
2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.
3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.
В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.