Что показывает коэффициент ковариации

Ковариация и коэффициент корреляции

Ранее была рассмотрена диаграмма разброса, иллюстрирующая распределение двумерных числовых данные (см. последний раздел Изображение двумерных числовых данных заметки Представление числовых данных в виде таблиц и диаграмм). В настоящей заметке мы изучим два количественных показателя, характеризующих силу зависимости между двумя переменными — ковариацию и коэффициент корреляции. [1] Ковариация оценивает силу линейной зависимости между двумя числовыми переменными X и Y. Выборочная ковариация:

Скачать заметку в формате Word или pdf, примеры в формате Excel2013

Рассмотрим пятилетнюю среднегодовую доходность и долю затрат в фондах с очень низким уровнем риска (рис. 1). Для расчета ковариации двух выборок в Excel до 2007 года используется функция =КОВАР(), начиная с версии 2010 – функция КОВАРИВЦИЯ.В().

Рис. 1. Пятилетняя среднегодовая доходность и доля затрат взаимных фондов с очень низким уровнем риска

Любопытно, что ковариация случайной величины с собой равна дисперсии:

Если ковариация положительна, то с ростом значений одной случайной величины, значения второй имеют тенденцию возрастать, а если знак отрицательный — то убывать. Однако только по абсолютному значению ковариации нельзя судить о том, насколько сильно величины взаимосвязаны, так как её масштаб зависит от их дисперсий. Масштаб можно отнормировать, поделив значение ковариации на произведение среднеквадратических отклонений (квадратных корней из дисперсий). При этом получается так называемый коэффициент корреляции Пирсона.

Относительная сила зависимости, или связи, между двумя переменными, образующими двумерную выборку, измеряется коэффициентом корреляции, изменяющимся от –1 для идеальной обратной зависимости до +1 для идеальной прямой зависимости. Коэффициент корреляции обозначается греческой буквой ρ. Линейность корреляции означает, что все точки, изображенные на диаграмме разброса, лежат на прямой (рис 2). На панели А изображена обратная линейная зависимость между переменными X и Y. Таким образом, коэффициент корреляции ρ равен –1, т.е., когда переменная X возрастает, переменная Y убывает. На панели Б показана ситуация, в которой между переменными X и Y нет корреляции. В этом случае коэффициент корреляции ρ равен 0, и, когда переменная X возрастает, переменная Y не проявляет никакой определенной тенденции: она ни убывает, ни возрастает. На панели В изображена линейная прямая зависимость между переменными X и Y. Таким образом, коэффициент корреляции ρ равен +1, и, когда переменная X возрастает, переменная Y также возрастает.

Рис. 2. Три вида зависимости между двумя переменными

Рис. 3. Шесть диаграмм разброса и соответствующие коэффициенты корреляции, полученные с помощью программы Excel

На панели А показана ситуация, в которой выборочный коэффициент корреляции r равен –0,9. Прослеживается четко выраженная тенденция: небольшим значениям переменной X соответствуют очень большие значения переменной Y, и, наоборот, большим значениям переменной X соответствуют малые значения переменной Y. Однако данные не лежат на одной прямой, поэтому зависимость между ними нельзя назвать линейной. На панели Б приведены данные, выборочный коэффициент корреляции между которыми равен –0,6. Небольшим значениям переменной X соответствуют большие значения переменной Y. Обратите внимание на то, что зависимость между переменными X и Y нельзя назвать линейной, как на панели А, и корреляция между ними уже не так велика. Коэффициент корреляции между переменными X и Y, изображенными на панели В, равен –0,3. Прослеживается слабая тенденция, согласно которой большим значениям переменной X, в основном, соответствуют малые значения переменной Y. Панели Г–Е иллюстрируют положительную корреляцию между данными — малым значениям переменной X соответствуют большие значения переменной Y.

Обсуждая рис. 3, мы употребляли термин тенденция, поскольку между переменными X и Y нет причинно-следственных связей. Наличие корреляции не означает наличия причинно-следственных связей между переменными X и Y, т.е. изменение значения одной из переменных не обязательно приводит к изменению значения другой. Сильная корреляция может быть случайной и объясняться третьей переменной, оставшейся за рамками анализа. В таких ситуациях необходимо проводить дополнительное исследование. Таким образом, можно утверждать, что причинно-следственные связи порождают корреляцию, но корреляция не означает наличия причинно-следственных связей.

Выборочный коэффициент корреляции:

В Excel для вычисления коэффициента корреляции используется функция =КОРРЕЛ() (рис. 4).

Рис. 4. Функция КОРРЕЛ в Excel

Итак, коэффициент корреляции свидетельствует о линейной зависимости, или связи, между двумя переменными. Чем ближе коэффициент корреляции к –1 или +1, тем сильнее линейная зависимость между двумя переменными. Знак коэффициента корреляции определяет характер зависимости: прямая (+) и обратная (–). Сильная корреляция не является причинно-следственной зависимостью. Она лишь свидетельствует о наличии тенденции, характерной для данной выборки.

[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 221–227

Источник

Ковариация | Covariance

Математически ковариация (англ. Covariance) представляет собой меру линейной зависимости двух случайных величин. В портфельной теории этот показатель используется для определения зависимости между доходностью определенной ценной бумаги и доходностью портфеля ценных бумаг. Чтобы рассчитать ковариацию доходности необходимо воспользоваться следующей формулой:

где k_i – доходность ценной бумаги в i-ом периоде;

— ожидаемая (средняя) доходность ценной бумаги;

p_i – доходность портфеля в i-ом периоде;

— ожидаемая (средняя) доходность портфеля;

n – количество наблюдений.

Следует отметить, что в знаменатель формулы подставляется (n-1), если ковариация рассчитывается на основании выборки из генеральной совокупности наблюдений. Если в расчетах учитывается вся генеральная совокупность, то в знаменатель подставляется n.

Пример. В таблице представлена динамика доходность акций Компании А и Компании Б, а также динамика доходности портфеля ценных бумаг.

Чтобы воспользоваться вышеприведенной формулой для расчета ковариации доходности каждой из акций с портфелем необходимо рассчитать среднюю доходность, которая составит:

Cov (k_Б, k_p) = ((4,25-5,031)(2,27-3,201) + (4,47-5,031)(2,39-3,201) + (4,68-5,031)(3,47-3,201) + (4,71-5,031)(3,21-3,201) + (4,77-5,031)(2,95-3,201) + (5,25-5,031)(2,97-3,201) + (5,45-5,031)(3,32-3,201) + (5,33-5,031)(3,65-3,201) + (5,55-5,031)(3,97-3,201) + (5,85-5,031)(3,81-3,201))/(10-1) = 0,242

Аналогичные расчеты можно произвести в Microsoft Excel при помощи функции «КОВАРИАЦИЯ.В» для выборки из генеральной совокупности или функции «КОВАРИАЦИЯ.Г» для всей генеральной совокупности.

Интерпретация ковариации

Значение коэффициента ковариации может быть как отрицательным, так и положительным. Его отрицательное значение говорит о том, что доходность ценной бумаги и доходность портфеля демонстрируют разнонаправленное движение. Другими словами, если доходность ценной бумаги будет расти, то доходность портфеля будет падать, и наоборот. Положительное значение свидетельствует о том, что доходность ценной бумаги и портфеля изменяются в одном направлении.

Низкое значение (близкое к 0) коэффициента ковариации наблюдается в том случае, когда колебания доходности ценной бумаги и доходности портфеля носят случайный характер.

Источник

Ковариация

которая может быть получена из первой формулы, используя свойства математического ожидания. Перечислим основные свойства ковариации.

1. Ковариация случайной величины с самой собой есть ее дисперсия.

2. Ковариация симметрична.

$$cov\left(X,\ Y\right)=cov\left(Y,\ X\right).$$

4. Постоянный множитель можно выносить за знак ковариации.

$$cov\left(cX,\ Y\right)=cov\left(X,\ cY\right)=c\cdot cov\left(X,\ Y\right).$$

5. Ковариация не изменится, если к одной из случайных величин (или двум сразу) прибавить постоянную величину:

$$cov\left(X+c,\ Y\right)=cov\left(X,\ Y+c\right)=cov\left(X+x,\ Y+c\right)=cov\left(X,\ Y\right).$$

9. Дисперсия суммы (разности) случайных величин равна сумме их дисперсий плюс (минус) удвоенная ковариация этих случайных величин:

$$D\left(X\pm Y\right)=D\left(X\right)+D\left(Y\right)\pm 2cov\left(X,\ Y\right).$$

$$M\left(X\right)=\sum^n_=-2\cdot 0,3+0\cdot 0,25+1\cdot 0,25+7\cdot 0,2=1,05.$$

$$M\left(Y\right)=\sum^n_=-6\cdot 0,25+0\cdot 0,4+3\cdot 0,35=-0,45.$$

$$M\left(XY\right)=\sum_x_iy_j>=0,1\cdot \left(-2\right)\cdot \left(-6\right)+0,2\cdot \left(-2\right)\cdot 3+0,05\cdot 1\cdot 3+0,1\cdot 7\cdot \left(-6\right)+0,1\cdot 7\cdot 3=-1,95.$$

Корреляция

Перечислим основные свойства коэффициента корреляции.

При копировании материала с сайта, обратная ссылка обязательна!

Источник

Русские Блоги

Популярное объяснение ковариации и коэффициента корреляции

Что такое ковариация (ковариация)?

Ковариация представляет собой общую ошибку двух переменных, которая отличается от дисперсии только одной переменной. Если тенденции изменения двух переменных одинаковы, то есть если одна из них больше, чем ее собственное ожидаемое значение, а другая также больше, чем ее собственное ожидаемое значение, то ковариация между двумя переменными положительна. Если тенденции изменения двух переменных противоположны, то есть одна из них больше, чем ее собственное ожидаемое значение, а другая меньше, чем ее собственное ожидаемое значение, то ковариация между двумя переменными отрицательна.

Это объяснение некой энциклопедии. и многое другое! Это еще более непонятно? Как для студентов нетехнических специальностей ясно и наглядно понять математические концепции ковариации и коэффициента корреляции? Это не имеет значения. Сегодня Red Stone использует яркие примеры, чтобы объяснить коэффициенты ковариации и корреляции простым для понимания образом.

1. Как возникает ковариация?

Проще говоря, ковариация отражает взаимосвязь между двумя переменными X и Y. Этот вид корреляции можно условно разделить на три типа: положительная корреляция, отрицательная корреляция и нерелевантность.

Что такое положительная корреляция? Например, чем больше площадь дома (X), тем выше общая цена дома (Y), а площадь дома положительно коррелирует с общей ценой дома;

Что такое отрицательная корреляция? Например, чем больше времени студент проводит за играми (X), тем хуже его успеваемость (Y), тогда игровое время и успеваемость имеют отрицательную корреляцию;

Что не имеет значения? Например, степень черного и белого цвета кожи человека (X) не имеет очевидной связи с его физическим здоровьем (Y), поэтому не имеет значения.

Давайте сначала рассмотрим первый случай, пусть переменная X и переменная Y будут соответственно:

X = [11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]

Y = [12 15 17 21 22 21 18 23 26 25 22 28 24 28 30 33 28 34 36 35]

Постройте совместное распределение X и Y по координатам:

Очевидно, что общий тренд Y увеличивается с увеличением X, то есть изменения Y и X происходят в одном направлении. В этом случае мы говорим, что X и Y положительно коррелированы.

Давайте снова рассмотрим второй случай, пусть переменная X и переменная Y будут соответственно:

X = [11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]

Y = [35 35 29 29 28 28 27 26 26 23 21 22 25 19 16 19 20 16 15 16]

Постройте совместное распределение X и Y по координатам:

Очевидно, что общая тенденция Y уменьшается с увеличением X, то есть изменения Y и X меняются местами. В этом случае мы говорим, что X и Y отрицательно коррелированы.

Давайте снова рассмотрим третий случай, пусть переменная X и переменная Y будут соответственно:

X = [11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]

Y = [16 16 28 17 20 26 20 17 21 15 12 29 24 25 16 15 21 13 17 25]

Постройте совместное распределение X и Y по координатам:

Очевидно, что нет никакой положительной или отрицательной корреляции между Y и X в общем тренде. В этом случае мы говорим, что X и Y не связаны.

На приведенном выше рисунке вся область разделена на четыре области I, II, III и IV посредством EX и EY, и большая часть X и Y распределена в областях I и III, и только небольшая часть распределена в областях II. и IV.

В области I, если выполняются X> EX и Y> EY, то (X-EX) (Y-EY)> 0;

В области II, если выполняется X EY, то (X-EX) (Y-EY) 0;

В области IV, если выполняются X> EX и Y 0; в областях II и IV (X-EX) (Y-EY) E ( X − E X ) ( Y − E Y ) > 0 E(X-EX)(Y-EY)>0 E ( X − E X ) ( Y − E Y ) > 0

Приведенная выше формула означает, что ожидание (X-EX) (Y-EY) больше нуля, то есть среднее значение (X-EX) (Y-EY) больше нуля.

Затем давайте посмотрим на отрицательную корреляцию между X и Y:

На приведенном выше рисунке большая часть X и Y распределена в областях II и IV, и только небольшая часть распределена в областях I и III.

Точно так же в регионах I и III (X-EX) (Y-EY)> 0; в областях II и IV (X-EX) (Y-EY) E ( X − E X ) ( Y − E Y ) 0 E(X-EX)(Y-EY) E ( X − E X ) ( Y − E Y ) 0

Приведенная выше формула означает, что математическое ожидание (X-EX) (Y-EY) меньше нуля, то есть среднее значение (X-EX) (Y-EY) меньше нуля.

Наконец, давайте посмотрим на ситуацию, когда X и Y не связаны:

На приведенном выше рисунке X и Y примерно равномерно распределены в областях I, II, III и IV.

Точно так же в регионах I и III (X-EX) (Y-EY)> 0; в областях II и IV (X-EX) (Y-EY) E ( X − E X ) ( Y − E Y ) = 0 E(X-EX)(Y-EY)=0 E ( X − E X ) ( Y − E Y ) = 0

Приведенная выше формула означает, что математическое ожидание (X-EX) (Y-EY) равно нулю, то есть среднее значение (X-EX) (Y-EY) равно нулю.

В итоге можно сделать следующие выводы:

Когда X и Y положительно коррелируют: E ( X − E X ) ( Y − E Y ) > 0 E(X-EX)(Y-EY)>0 E ( X − E X ) ( Y − E Y ) > 0

Когда X и Y отрицательно коррелируют: E ( X − E X ) ( Y − E Y ) 0 E(X-EX)(Y-EY) E ( X − E X ) ( Y − E Y ) 0

Когда X и Y не связаны: E ( X − E X ) ( Y − E Y ) = 0 E(X-EX)(Y-EY)=0 E ( X − E X ) ( Y − E Y ) = 0

Поэтому мы ввели понятие ковариации, которая представляет собой числовую характеристику, которая выражает взаимосвязь между X и Y. Мы определяем ковариацию как:

По результатам предыдущего обсуждения,

Когда Cov (X, Y)> 0, X и Y положительно коррелируют;

Здесь причиной деления на N-1 вместо N является объективная оценка общего ожидания выборки. Кстати, если Y = X, то ковариация представляет собой дисперсию X.

Ниже мы вычисляем ковариацию X и Y в трех вышеупомянутых случаях соответственно по формуле ковариации.

Когда X и Y положительно коррелированы, Cov (X, Y) = 37,3684;

2. Какая связь между коэффициентом корреляции и ковариацией?

Мы уже знаем, что такое ковариация и откуда берется формула ковариации. Если мы знаем взаимосвязь между ковариацией двух переменных X и Y и нуля, мы можем сделать вывод, являются ли X и Y коррелированными положительно, отрицательно или некоррелированными. Тогда возникает вопрос: отражает ли величина ковариации степень корреляции? То есть, если ковариация равна 100, обязательно ли она сильнее, чем положительная корреляция с ковариацией 10?

Взгляните на пример ниже!

Переменные X1 и Y1:

X1 = [11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]

Y1 = [12 12 13 15 16 16 17 19 21 22 22 23 23 26 25 28 29 29 31 32]

Переменные X2 и Y2:

X2 = [110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 260 270 280 290 300]

Y2 = [113 172 202 206 180 184 242 180 256 209 288 255 240 278 319 322 345 289 333 372]

Диаграммы совместного распределения X1, Y1 и X2, Y2 следующие:

Очевидно, из рисунка видно, что X1, Y1 и X2, Y2 все положительно коррелируют, и степень положительной корреляции между X1 и Y1, очевидно, больше, чем у X2 и Y2. Затем мы вычисляем ковариацию двух графиков, чтобы увидеть, так ли это.

авария! Ковариация X2 и Y2 в 100 раз больше, чем ковариация X1 и Y1. Не похоже, что чем больше ковариация, тем выше степень положительной корреляции. Это, в конце концов, почему?

Фактически, причина такой ситуации в том, что величины числовых изменений в двух ситуациях различаются (или различаются размеры). При вычислении ковариации мы не учитывали разницу в амплитуде различных переменных, и не существует единого стандарта измерения при сравнении ковариации.

Следовательно, чтобы устранить этот эффект, чтобы точно получить степень сходства между переменными, нам необходимо разделить ковариацию на стандартное отклонение соответствующих переменных. Таким образом получается выражение коэффициента корреляции:

Можно видеть, что коэффициент корреляции делится на стандартное отклонение переменных X и Y на основе ковариации. Формула для расчета стандартного отклонения:

Почему деление на стандартное отклонение соответствующих переменных устраняет влияние амплитуды? Это связано с тем, что само стандартное отклонение отражает степень изменения амплитуды переменной.Деление на стандартное отклонение может просто компенсировать его и стандартизировать ковариацию. Таким образом, диапазон коэффициента корреляции нормализуется до [-1,1].

Затем мы вычислим коэффициенты корреляции X1, Y1 и X2, Y2 в приведенном выше примере.

Итак, мы получаем, что коэффициент корреляции между X1 и Y1 больше, чем коэффициент корреляции между X2 и Y2. Это соответствует реальной ситуации. Другими словами, исходя из коэффициента корреляции, мы можем определить степень корреляции между двумя переменными и сделать следующие выводы:

Коэффициент корреляции больше нуля, это означает, что две переменные положительно коррелированы, и чем больше коэффициент корреляции, тем выше положительная корреляция;

Коэффициент корреляции меньше нуля, это означает, что две переменные имеют отрицательную корреляцию, и чем меньше коэффициент корреляции, тем выше отрицательная корреляция;

Коэффициент корреляции равен нулю, что означает, что две переменные не коррелированы.

Источник

Повторение статистики для начала путешествия по науке о данных

Введение

Предположим, у нас есть диаграмма рассеяния, на которой каждая точка — это человек. На одной оси показан его профессиональный опыт в годах, на другой — доход.

В соответствии с диаграммой справа можно заключить, что между опытом и доходом нет никакой связи, то есть определенный опыт оплачивается по-разному.

Слева, наоборот, между признаками существует четкая линейная зависимость.

Ковариация и корреляция показывают, насколько тесно между собой связаны переменные набора данных.

N.B: в приведенном примере представлен двумерный вид данных (с двумя переменными). На практике статистики используют многомерные данные (со множеством переменных).

Ковариация

Ковариация — это мера зависимости между двумя или более случайных переменных.

С английского «covariance» = «co» (совместность/соединение) + «variance» (дисперсия). То есть ковариация похожа на дисперсию, но она применяется для сравнения двух переменных, где вместо суммы квадратов, мы получаем сумму векторного произведения.
Дисперсия показывает, насколько определенная переменная отличается от среднего значения, а ковариация — насколько две переменные отличаются друг от друга. Таким образом, можно утверждать следующее:

Ковариация измеряет дисперсию между двумя переменными.

Ковариация может быть отрицательной, положительной и нулевой: положительное значение показывает, что две переменные изменяются в одном направлении (если одна переменная увеличивается, то и вторая тоже увеличивается); отрицательное значение показывает, что две переменные изменяются в разных направлениях (одна увеличивается, вторая уменьшается); нулевая ковариация означает, что они изменяются независимо друг от друга.

Формула

Формулу сложно объяснить, но важно понять, что она означает:

Ковариация между переменными X и Y

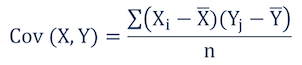
Предположим, что набор данных со случайными переменными представлен в виде вектора. Тогда в прошлом примере у нас есть два вектора для опыта и дохода. Ниже приведен порядок действий:

На втором этапе измеряется угол между двумя векторами. Если угол острый, то переменные тесно связаны между собой.

Ограниченность

Следует отметить, что несмотря на то, что ковариация измеряет зависимость между направлениями двух переменных, она не показывает тесноту этой зависимости.

На практике самая большая проблема с этой мерой заключается в том, что она зависит от используемой единицы измерения. Например, необходимо перевести годы опыта в месяцы. Тогда ковариация будет в 12 раз больше.

В этом случае на помощь приходит корреляция!

Корреляция

Корреляция — одна из наиболее распространенных мер в статистике, описывающая тесноту взаимосвязи между двумя случайными переменными. Она считается нормализованной версией ковариации. Давайте рассмотрим, почему…

Формула

Корреляция (обозначаемая греческой буквой «ро» — ρ) рассчитывается по следующей формуле:

Обратите внимание, что функциональная связь редко встречается на практике, так как две случайные переменные обычно не сопоставляются друг с другом на основе постоянного значения.

Корреляция, равная 0, означает, что между двумя переменными нет линейной зависимости. Тогда может быть отношение x = y².

Ключевые свойства

Корреляция — безразмерная величина, указывающая не только на направление взаимосвязи, но и на ее тесноту (в зависимости от того, насколько большим является абсолютное значение). Единицы измерения исключены из-за того, что ковариацию разделили на среднеквадратическое отклонение.

Напоследок необходимо запомнить, что корреляция не является причинно-следственной связью. Высокая корреляция между двумя случайными переменными просто означает, что они связаны друг с другом, но их взаимоотношение не обязательно должен иметь причинно-следственный характер. Доказать причинно-следственную связь можно только с помощью контролируемых экспериментов, при которых внешние переменные исключаются и эффекты двух данных переменных изолируются.

Источник