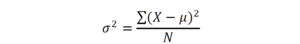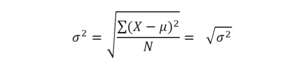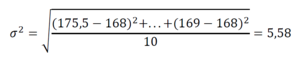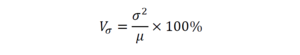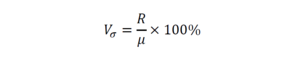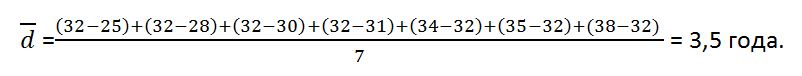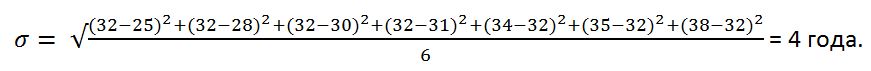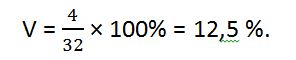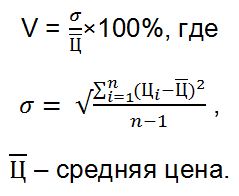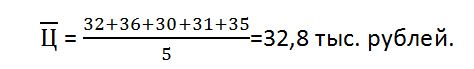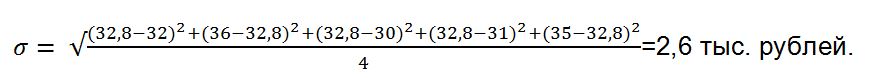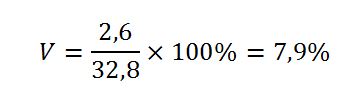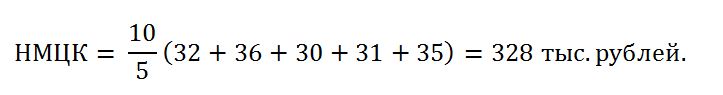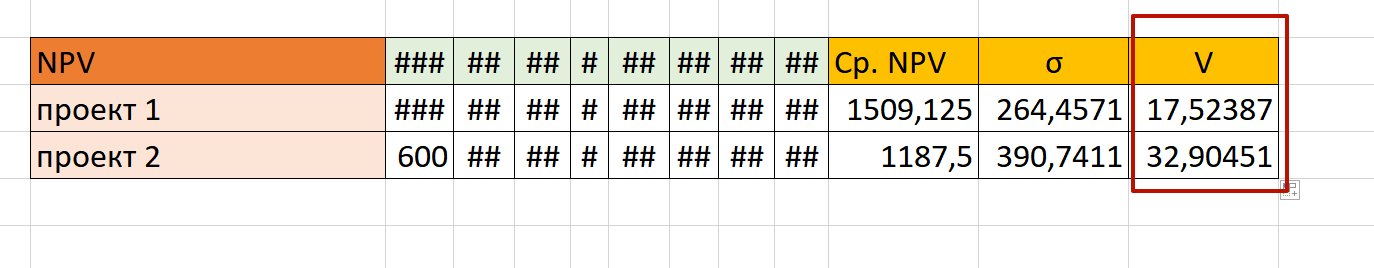Что показывает коэффициент вариации
Статистические параметры
Дисперсия
Полученные из опыта величины неизбежно содержат погрешности, обусловленные самыми разнообразными причинами. Среди них следует различать погрешности систематические и случайные. Систематические ошибки обусловливаются причинами, действующими вполне определенным образом, и могут быть всегда устранены или достаточно точно учтены. Случайные ошибки вызываются весьма большим числом отдельных причин, не поддающихся точному учету и действующих в каждом отдельном измерении различным образом. Эти ошибки невозможно совершенно исключить; учесть же их можно только в среднем, для чего необходимо знать законы, которым подчиняются случайные ошибки.
Будем обозначать измеряемую величину через А, а случайную ошибку при измерении х. Так как ошибка х может принимать любые значения, то она является непрерывной случайной величиной, которая вполне характеризуется своим законом распределения.
Наиболее простым и достаточно точно отображающим действительность (в подавляющем большинстве случаев) является так называемый нормальный закон распределения ошибок:
Этот закон распределения может быть получен из различных теоретических предпосылок, в частности, из требования, чтобы наиболее вероятным значением неизвестной величины, для которой непосредственным измерением получен ряд значений с одинаковой степенью точности, являлось среднее арифметическое этих значений. Величина 
Среднее арифметическое
Определение дисперсии по опытным данным. Если для какой-либо величины А непосредственным измерением получено n значений ai с одинаковой степенью точности и если ошибки величины А подчинены нормальному закону распределения, то наиболее вероятным значением А будет среднее арифметическое:
Для определения дисперсии нормального закона распределения ошибок в этом случае пользуются формулой:
Среднеквадратическое отклонение
Среднеквадратическое отклонение показывает абсолютное отклонение измеренных значений от среднеарифметического. В соответствии с формулой для меры точности линейной комбинации средняя квадратическая ошибка среднего арифметического определяется по формуле:
Коэффициент вариации
Коэффициент вариации характеризует относительную меру отклонения измеренных значений от среднеарифметического:
Чем больше значение коэффициента вариации, тем относительно больший разброс и меньшая выравненность исследуемых значений. Если коэффициент вариации меньше 10%, то изменчивость вариационного ряда принято считать незначительной, от 10% до 20% относится к средней, больше 20% и меньше 33% к значительной и если коэффициент вариации превышает 33%, то это говорит о неоднородности информации и необходимости исключения самых больших и самых маленьких значений.
Среднее линейное отклонение
Для проверки соответствия исследуемых значений закону нормального распределения применяют отношение показателя асимметрии к его ошибке и отношение показателя эксцесса к его ошибке.
Показатель асимметрии
Показатель асимметрии (A) и его ошибка (ma) рассчитывается по следующим формулам:
Показатель эксцесса
Показатель эксцесса (E) и его ошибка (me) рассчитывается по следующим формулам:
Если А 0, то больше данных с меньшими значениями, чем среднеарифметическое.
Если Е 0, то данные сконцентрированы около среднеарифметического значения.
При отношении А/ma и E/me меньше 3 анализируемая информация подчиняется закону нормального распределения.
Программная реализация данной методики финансовой математики произведена в: «Альтаир Финансовый калькулятор 2.xx».
На примере расчета среднего арифметического, дисперсии, вариации, среднеквадратического отклонения можно увидеть, как применять программу «Альтаир Финансовый калькулятор 2.xx» на практике.

Главная 



Copyright © 2021 by Altair Software Company. Потенциальным спонсорам программ и проекта.
Коэффициент вариации (CV)
Коэффициент вариации (coefficient of variation, CV) — это статистическая мера дисперсии (разброса) данных вокруг некоторого среднего значения. Коэффициент вариации представляет собой отношение среднеквадратичного отклонения к среднему значению и является весьма полезной величиной для сравнения степени вариации при переходе от одного ряда данных к другому, даже если их средние значения резко отличаются друг от друга.
Понимание коэффициента вариации
Коэффициент вариации показывает степень изменчивости некоторой выборки данных по отношению к среднему их значению. В финансах данный коэффициент позволяет инвесторам определить, насколько велика волатильность, или риск, по сравнению с величиной ожидаемой прибыли от инвестиций.
Чем меньше значение CV, тем лучший компромисс наблюдается между риском и доходностью. Обратите внимание, что если ожидаемая доходность в знаменателе отрицательна или равна нулю, полученное значение коэффициента может ввести вас в заблуждение.
Коэффициент вариации может быть весьма полезен при использовании соотношения риск/прибыль для выбора объекта инвестиций. Например, инвестор не склонный к риску будет рассматривать активы с исторически низкой степенью волатильности и высокой степенью доходности по отношению к общему рынку (или к отдельной отрасли). И наоборот, инвесторы склонные к риску, будут стремиться инвестировать в активы с исторически высокой степенью волатильности.
Формула CV может использоваться для определения дисперсии между исторической средней ценой и текущими показателями цены акции, товара или облигации.
Обычно данный коэффициент используют в таких целях как:
КЛЮЧЕВЫЕ МОМЕНТЫ
Формула CV
Ниже приведена формула для расчета коэффициента вариации:
Обратите внимание, что если значение ожидаемой доходности в знаменателе формулы коэффициента вариации отрицательна или равна нулю, то результат расчёта по ней нельзя считать корректным.
Коэффициент вариации в Excel и Open Office
Коэффициент вариации можно достаточно легко рассчитать в Excel. Несмотря на то, что в нём нет стандартной функции для расчёта CV, но зато есть функции позволяющие рассчитать стандартное отклонение (СТАНДОТКЛОН) и среднее значение (СРЗНАЧ). Сначала используйте функцию стандартного отклонения, затем вычислите среднее значение, а после этого разделите ячейку, содержащую стандартное отклонение, на ячейку содержащую среднее значение.
В Open Office данный показатель рассчитывается аналогично. Функция стандартного отклонения здесь — STDEV, а функция среднего значения — AVERAGE.
Давайте рассмотрим пример расчёта коэффициента вариации в Open Office. Предположим, что у нас есть три потенциальных объекта для инвестиций — объект А, объект Б и объект В. Прибыль по каждому из этих проектов за последние 6 лет занесена в таблицу представленную ниже:
Давайте рассчитаем значение CV для каждого из этих объектов. Начнём с расчёта стандартных отклонений. Для этого применим к ряду значений прибыли отдельно по каждому объекту функцию STDEV:
Аналогичным образом рассчитаем среднее значение для каждого ряда данных:
Наконец рассчитаем CV. Для этого разделим полученные значения отклонений на средние значения. В результате получим следующую таблицу:
Кликните по картинке для увеличения
Очевидно, что из всех представленных объектов инвестиций предпочтительным будет объект Б имеющий наименьшее значение коэффициента CV.
Пример использования коэффициента вариации для выбора объекта инвестиций
Рассмотрим инвестора не склонного к риску, который хочет инвестировать в биржевой фонд (ETF) состоящий из корзины ценных бумаг отслеживающей индекс широкого рынка. Инвестор выбирает SPDR S&P 500 ETF, Invesco QQQ ETF и iShares Russell 2000 ETF. Затем он анализирует доходность и волатильность выбранных ETF за последние 15 лет и предполагает, что в будущем они могут иметь аналогичную доходность в отношении к своим долгосрочным средним значениям.
Для принятия решения инвестором используется следующая 15-летняя историческая информация:
Исходя из этих данных, инвестор может инвестировать либо в SPDR S&P 500 ETF, либо в iShares Russell 2000 ETF, так как соотношение риска и вознаграждения для них является сравнительно одинаковым. А для Invesco QQQ ETF соотношение риск-доходность, как видите, будет несколько хуже.
Коэффициент вариации в статистике: примеры расчета

Показатели описательной статистики
Существует несколько показателей, которые использует описательная статистика.
Среднее арифметическое
Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):
168, 171, 175, 177, 179, 187, 174, 176, 179, 169.
Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:
Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться. Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического. Если обратиться к росту студентов, то формула будет выглядеть следующим образом:
Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)
Если свести все к строгим математическим терминам, то определение среднего арифметического (обозначается греческой буквой – μ («мю»)) будет звучать так:
Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).
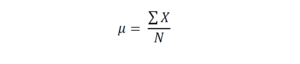
Стандартное отклонение
Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.
На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:
Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:
Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:
Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.
Коэффициент вариации
Среднее квадратичное отклонение хорошо работает с рядами, в которых разброс значений не очень велик (это хорошо прослеживалось на примере роста, где интервал был всего 18 см). Если бы ряд наших измерений был значительнее, а варьирование роста было сильнее, то стандартное отклонение стало непоказательным и нам потребовался бы критерий, который может отразить разброс в относительных единицах (т. е. в процентах, относительно средней величины).
Для этих целей предусмотрены абсолютные и относительные показатели вариации в статистике, характеризующие вариационные масштабы:
Квадратический коэффициент вариации (обозначается как Vσ) – это отношение среднеквадратичного отклонения к среднеарифметическому значению, выраженное в процентах.
Для нашего примера со студентами, определить Vσ несложно — он будет равен 3,18%. Основная закономерность – чем больше будет изменяться значение коэффициента, тем больше разброс вокруг среднего значения и тем менее однородна выборка.
Преимущество коэффициента вариации в том, что он показывает однородность значений (асимметрия) в ряду наших измерений, кроме того, на него не оказывают влияния масштаб и единицы измерения. Эти факторы делают коэффициент вариации особенно популярным в биомедицинских исследованиях. Будет считаться, что эксцесс значения Vσ =33% отделяет однородные выборки от неоднородных.
Если найти в ряду значений роста (первый пример) максимальное и минимальное значения, то получим размах вариации (обозначается как R, иногда ещё называется колеблемостью). В нашем примере – это значение будет равно 18 см. Эта характеристика используется для расчёта коэффициента осцилляции:
Коэффициент осцилляции – показывает как размах вариации будет относиться к среднему арифметическому ряда в процентном отношении.
Расчёты в Microsoft Ecxel 2016
Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:
| Наименование показателя | Расчёт в Excel 2016* |
| Среднее арифметическое | =СРГАРМ(A1:A10) |
| Дисперсия | =ДИСП.В(A1:A10) |
| Среднеквадратический показатель | =СТАНДОТКЛОН.В(A1:A10) |
| Коэффициент вариации | =СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10) |
| Коэффициент осцилляции | =(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10) |
* в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.
Итак, обобщим информацию:
Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила коэффициент вариации, который является мерой однородности данных.
Коэффициент вариации: для чего нужен, расчет, примеры, упражнения
Содержание:
В коэффициент вариации (CV) выражает стандартное отклонение относительно среднего. То есть он пытается объяснить, насколько велико значение стандартного отклонения по отношению к среднему.
Например, переменный рост четвероклассников имеет коэффициент вариации 12%, что означает, что стандартное отклонение составляет 12% от среднего значения.
Обозначается CV, коэффициент вариации является безразмерным и получается делением стандартного отклонения на среднее значение и умножением на сто.
Чем меньше коэффициент вариации, тем меньше отклонение данных от среднего. Например, в переменной со средним значением 10 и другой со средним значением 25, обе со стандартным отклонением 5, их коэффициенты вариации составляют 50% и 20% соответственно. Конечно, первая переменная более изменчива (дисперсия), чем вторая.
Рекомендуется работать с коэффициентом вариации для переменных, измеряемых в шкале пропорций, то есть шкалах с абсолютным нулем независимо от единицы измерения. Примером может служить переменная расстояния, которая не имеет значения, измеряется она в ярдах или метрах, ноль ярдов или ноль метров означает одно и то же: нулевое расстояние или смещение.
Для чего нужен коэффициент вариации?
Коэффициент вариации служит для:
— Коэффициент вариации часто используется как показатель надежности в научных экспериментах. Говорят, что если коэффициент вариации составляет 30% или больше, результаты эксперимента следует отбросить из-за их низкой надежности.
— Это позволяет предсказать, насколько сгруппированы вокруг среднего значения изучаемой переменной, даже не зная ее распределения. Это очень помогает при оценке ошибок и вычислении размеров выборки.
Предположим, что переменные вес и рост людей измеряются в совокупности. Вес с CV 5% и рост с CV 14%. Если вы хотите взять выборку из этой совокупности, размер выборки должен быть больше для оценок роста, чем для веса, поскольку существует большая вариативность в измерении роста, чем в измерении веса.
Важное наблюдение за полезностью коэффициента вариации заключается в том, что он теряет смысл, когда значение среднего близко к нулю. Среднее значение является делителем вычисления CV, и, следовательно, очень маленькие его значения приводят к тому, что значения CV будут очень большими и, возможно, не поддающимися вычислению.
Как рассчитывается?
Расчет коэффициента вариации относительно прост, достаточно знать среднее арифметическое и стандартное отклонение набора данных, чтобы рассчитать его по формуле:
Если они неизвестны, но данные доступны, можно предварительно рассчитать среднее арифметическое и стандартное отклонение, используя следующие формулы:
Примеры
Пример 1
Были измерены веса в кг группы из 6 человек: 45, 62, 38, 55, 48, 52. Мы хотим знать коэффициент вариации переменной веса.
Он начинается с вычисления среднего арифметического и стандартного отклонения:
Ответ: коэффициент вариации переменного веса 6 человек в выборке составляет 16,64%, при среднем весе 50 кг и стандартном отклонении 8,32 кг.
Пример 2
В отделении неотложной помощи больницы измеряют температуру тела в градусах Цельсия у 5 детей, находящихся на лечении. Результаты 39-е, 38-е, 40-е, 38-е и 40-е. Какой коэффициент вариации переменной температуры?
Он начинается с вычисления среднего арифметического и стандартного отклонения:
Теперь он подставляется в формулу для коэффициента вариации:
Ответ: коэффициент вариации температурной переменной для 5 детей в выборке составляет 2,56%, при средней температуре 39 ° C и стандартном отклонении 1 ° C.
Что касается температуры, то следует проявлять осторожность при обращении с весами, поскольку, будучи переменной, измеряемой в интервальной шкале, она не имеет абсолютного нуля. В рассматриваемом случае, что бы произошло, если бы температуры были преобразованы из градусов Цельсия в градусы Фаренгейта:
Рассчитываются среднее арифметическое и стандартное отклонение:
Теперь он подставляется в формулу для коэффициента вариации:
Ответ: коэффициент вариации температурной переменной у 5 детей в выборке составляет 1,76%, при средней температуре 102,2 ° F и стандартном отклонении 1,80 ° F.
Решенные упражнения
Упражнение 1
Вес в кг 10 сотрудников почтового отделения был измерен: 85, 62, 88, 55, 98, 52, 75, 70, 76, 77. Мы хотим знать коэффициент вариации переменной веса.
Рассчитываются среднее арифметическое и стандартное отклонение:
Теперь он подставляется в формулу для коэффициента вариации:
Ответ: коэффициент вариации переменного веса 10 человек в почтовом отделении составляет 19,74%, при среднем весе 73,80 кг и стандартном отклонении 14,57 кг.
Упражнение 2.
В одном городе измеряется рост 9 465 детей во всех школах первого класса, средний рост составляет 109,90 см со стандартным отклонением 13,59 см. Рассчитайте коэффициент вариации.
Ответ: коэффициент вариации переменного роста первоклассников города составляет 12,37%.
Упражнение 3.
Смотритель парка подозревает, что популяции черных и белых кроликов в его парке не имеют одинаковой изменчивости в размерах. Чтобы продемонстрировать это, он взял образцы по 25 кроликов из каждой популяции и получил следующие результаты:
— Белые кролики: средний вес 7,65 кг и стандартное отклонение 2,55 кг.
-Черные кролики: средний вес 6,00 кг и стандартное отклонение 2,43 кг.
Смотритель парка прав? Ответ на гипотезу смотрителя парка можно получить с помощью коэффициента вариации:
Ответ: коэффициент вариации веса черных кроликов почти на 7% больше, чем у белых кроликов, поэтому можно сказать, что смотритель парка прав в своем подозрении, что вариабельность веса двух популяций кроликов не равны.
Ссылки
Эффект кросса: что это такое и как влияет на восприятие
Маркетинг для психологов: команда «Психология и разум» к услугам вашей клиники
Что такое коэффициент вариации и для чего он нужен
Коэффициент вариации – это статистический показатель, какой широко используется в финансовых расчетах. Он показывает степень разброса значений в числовой последовательности. А именно, насколько любая из величин отклоняется от средней. Если вариация слишком высока, то оценивать среднее значение некорректно. В этой ситуации обыкновенно исключают минимальное и максимальное число.
Показатель чаще всего применяется при формировании начальной минимальной цены контракта по 44-ФЗ. Она должна опираться на выборке рыночных цен, а в их оценке как раз и используется вариация. Кроме того, применяется при анализе рисков инвестиционных проектов и доходности ценных бумаг. В цельном, показатели вариации применимы в любой сфере, где требуется оценить совокупность данных и их разнообразие: статистика, математика, экономический разбор, социология, маркетинг и т.д.
Формулы расчета в статистике
Для оценки совокупности значений и их однородности применяют следующие инструменты:
Рассмотрим применение указанных формул на примере оценки среднего возраста трудящихся в отделе кадров. В указанном подразделении трудятся 7 сотрудников, которым 25, 28, 30, 31, 34, 35 и 38 лет. Размах вариации покажет нам разницу в году между самым младшим и самым старшим из них:
Рассчитаем среднее линейное отклонение. Для этого для начала найдем посредственный возраст в отделе: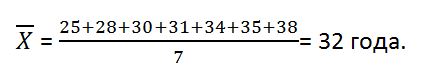
Соответственно, мы можем сказать, что средний возраст сотрудников составляет 32 ± 3,5 года.
Среднеквадратичное отклонение покажет то же самое, но немало точно:
Коэффициент вариации покажет, на сколько процентов возраст каждого работника отличается от среднего по отделу:
Оценка коэффициента вариации
Если со посредственными значениями и отклонениями от них все понятно, то зачем же рассчитывается коэффициент вариации? С его помощью можно судить, насколько показательно усредненное смысл и можно ли по нему судить о выборке в целом. В нашем примере он позволит ответить на вопрос, можно ли утверждать то, что посредственный возраст по отделу кадров составляет 32 года. Либо реальные показатели будут слишком сильно выделяться от полученного значения?
В статистике определены следующие критерии оценки:
Если показатель вариации превышает 33%, то выборка почитается неоднородной и судить о ней по средним значениям никак нельзя. При незначительном разбросе достоверность средних будет максимальной. В нашем образце вариативность средняя и в целом оценивать возраст по средним значениям с учетом отклонений вполне можно.
Если посмотреть на числовой ряд, то видать, что только 2 сотрудника существенно отклоняются от среднего возраста. На практике при слишком высокой вариативности из анализа исключают максимальное и минимальное смыслы, после чего проводят повторную проверку. Также часто по коэффициенту вариации сравнивают разные выборки. В нашем образце это слабо применимо, но, например, при анализе цен конкурентов будет вполне эффективно для выбора наиболее подходящей для анализа совокупности смыслов.
Читайте также! Выплата дивидендов учредителям ООО и АО в 2019 году
Применение при закупках по 44-ФЗ
Федеральный закон 44-ФЗ регулирует распорядок проведения государственных закупок. Его цель – не допустить злоупотреблений должностных лиц и передачу контрактов «своим» фирмам по завышенным/заниженным стоимостям. Именно для этого в законе определен порядок того, как устанавливается начальная минимальная цена контракта (НМЦК) – та, с какой и будут начинаться торги.
Методика определения начальной минимальной цены
Законом предусмотрено 5 методов определения НМЦК:
При этом наиболее предпочтительным и рекомендуемым является именно первоначальный. Его суть в том, что анализируются цены точно таких же товаров или услуг (идентичных) либо при их отсутствии схожих (однородных). Оба понятия четко установлены:
Данный порядок определен статьей 22 вышеуказанного закона. В 2019 году в нее было привнесено несколько изменений:
Как рассчитать НМЦК
Для расчета начальной цены заказчику необходимо составить выборку рыночных цен. Это можно сделать вытекающими способами:
Обычно используется первый способ. Нескольким поставщикам отправляются запросы введённой формы, а на основании полученных ответов и осуществляются расчеты по следующей формуле:
Коэффициент вариации в данном случае предзнаменований вид:
Пример расчета
Рассмотрим, как рассчитать НМЦК и коэффициент вариации на примере закупки 10 холодильников для больницы. От 5 поставщиков бывальщины получены коммерческие предложения со следующими ценами: 32, 36, 30, 31 и 35 тыс. рублей за штуку.
Оценим однородность ценовых предложений линией расчета коэффициента вариации. Для начала рассчитаем среднюю цену:
Теперь необходимо найти среднеквадратичное отклонение:
И, наконец, рассчитываем коэффициент вариации:
V меньше 10%, таким манером, делаем вывод о том, что выборка однородна и ее можно использовать для установки закупочных цен для торгов.
Посчитаем минимальную цену контракта:
Использование в оценке рисков
В финансовом разборе степень отклонения показателя от среднего значения показывает уровень риска. Например, если прибыль в разные годы существования компании то существенно всходит, то падает в убыток, инвестировать в нее опасно. То же самое касается ценных бумаг и любых других биржевых инструментов. Самыми привлекательными будут стабильные бумаги с минимальными колебаниями котировок при неплохом росте. Таким образом, есть еще два направления, где активно используется коэффициент вариации: оценка рисков проекта и рисков по доходности ценных бумаг.
Декламируйте также! Организация и внедрение бережливого производства на предприятии
Инвестиционные проекты
Как правило, при оценке рисков инвестиционных проектов используются:
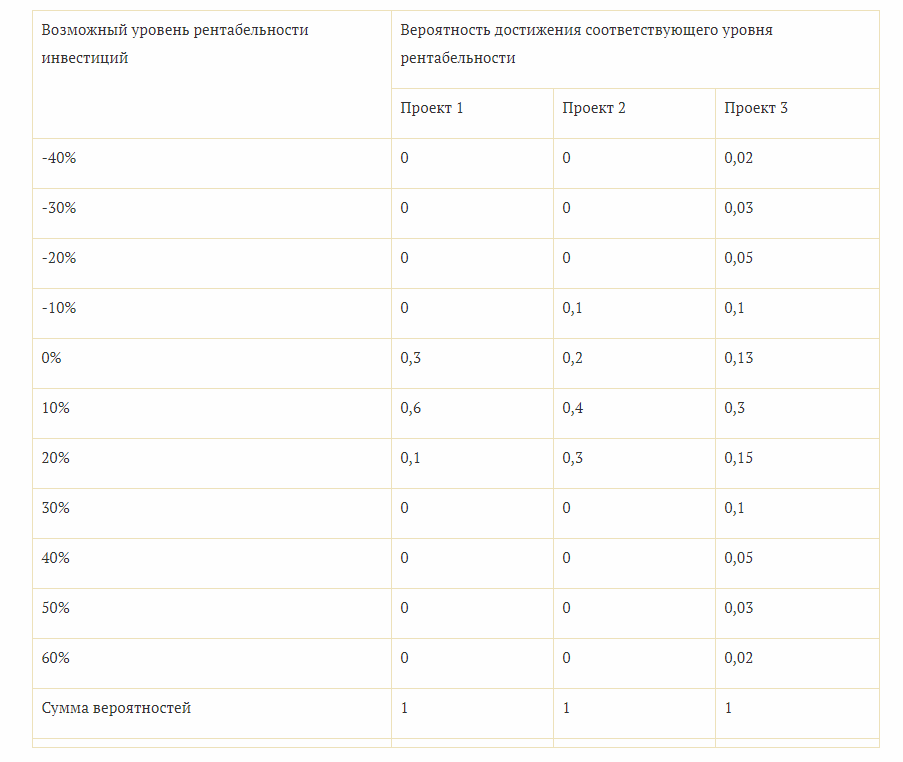
Обычно сравниваются несколько проектов по всем критериям. Также есть вариант рассмотреть возможность достижения того или другого уровня рентабельности:
В данном случае все проекты будут рискованными, поскольку коэффициент вариации составит 65%, 95% и 198% соответственно. Но риск по первому немало чем в 2 раза ниже, чем по третьему, поэтому из представленных вариантов лучше выбрать его.
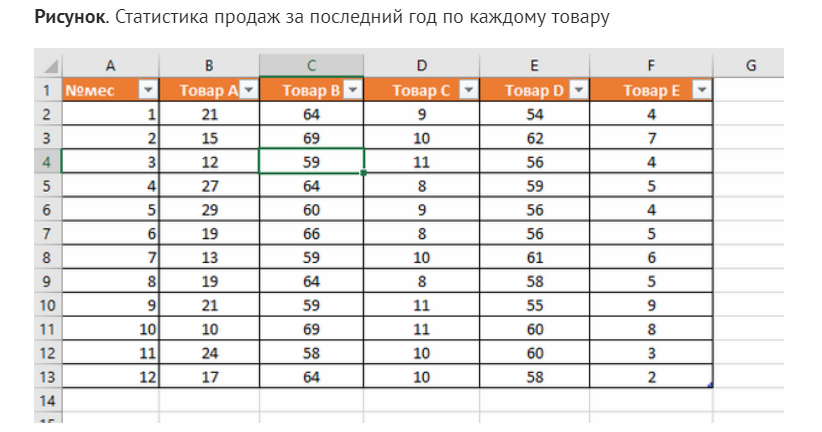
Нередко используют коэффициент при анализе спроса и принятии решении о закупках. Так, анализируется статистика продаж товара, после чего определяется, что закупать в первую очередь, а что только при наличии предзаказа:
В этом примере коэффициенты вариации по товарам А, B, C, D и E будут равны 30%, 6%, 12%, 4%, 38% соответственно. Очевидно, что спрос на продукцию E нестабилен и мощно колеблется в разные месяцы, поэтому заказывать целую партию рискованно.
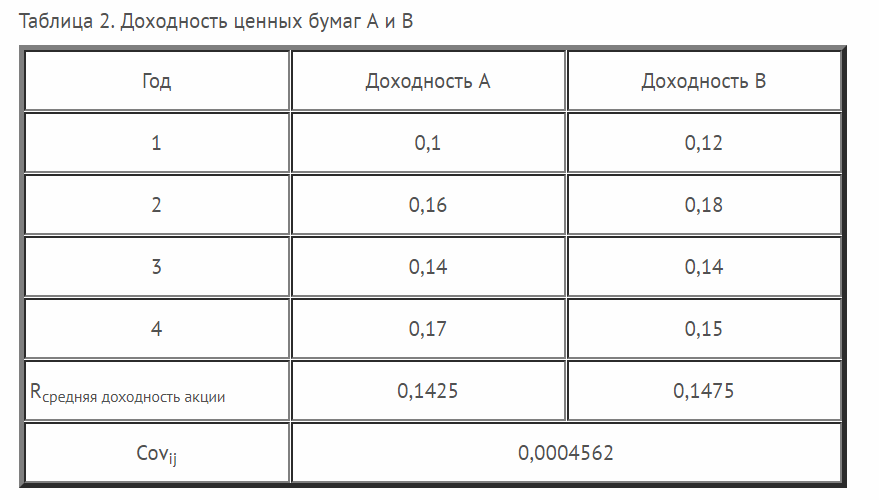
Ценные бумаги
Что касается торговли на бирже, то тут можно оценивать в двух вариантах:
В первом случае, имея эти о колебаниях котировок в прошлом, мы сможем оценить риск вложения именно в данный инструмент. Во втором варианте можно оценить риск портфеля инвестиций на основании совокупности доходности любой его составляющей. Также риск портфеля можно проанализировать на основании совокупности вариаций каждой его составляющей во временном интервале. Все эти методики используются в комплексном анализе рисков инвестиционного портфеля.
Расчет в MS Excel
Как при расчете цены контракта, так и при оценке инвестиционных проектов выполнять громоздкие вычисления квадратичного отклонения и коэффициента вариации вручную весьма трудоемко. Поэтому рассмотрим, как быстро и просто выполнить это при помощи электронной таблицы Excel.
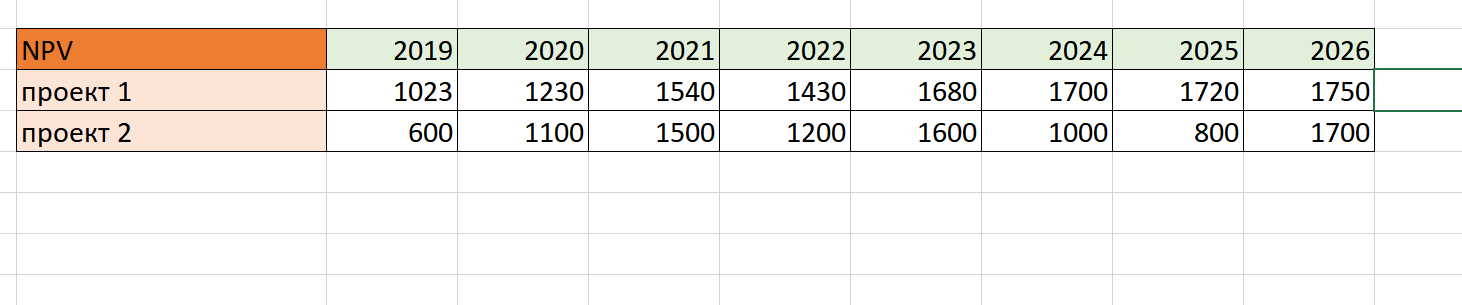
Для начала открываем редактор и создаем таблицу с отправными данными. Для примера возьмем два инвестиционных проекта с показателями NPV за 8 лет.
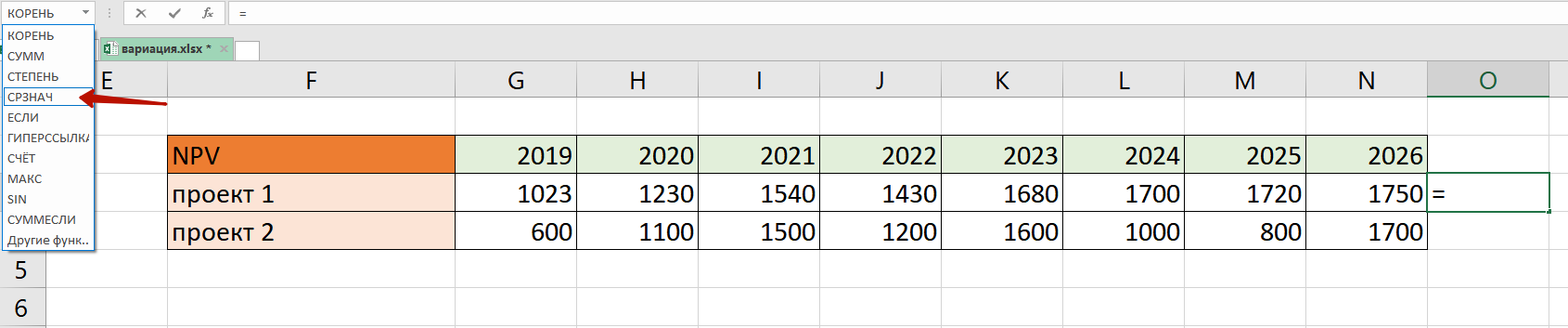
Далее находим среднее значение прибыли при помощи функции СРЗНАЧ:
Вышли вот такие значения:
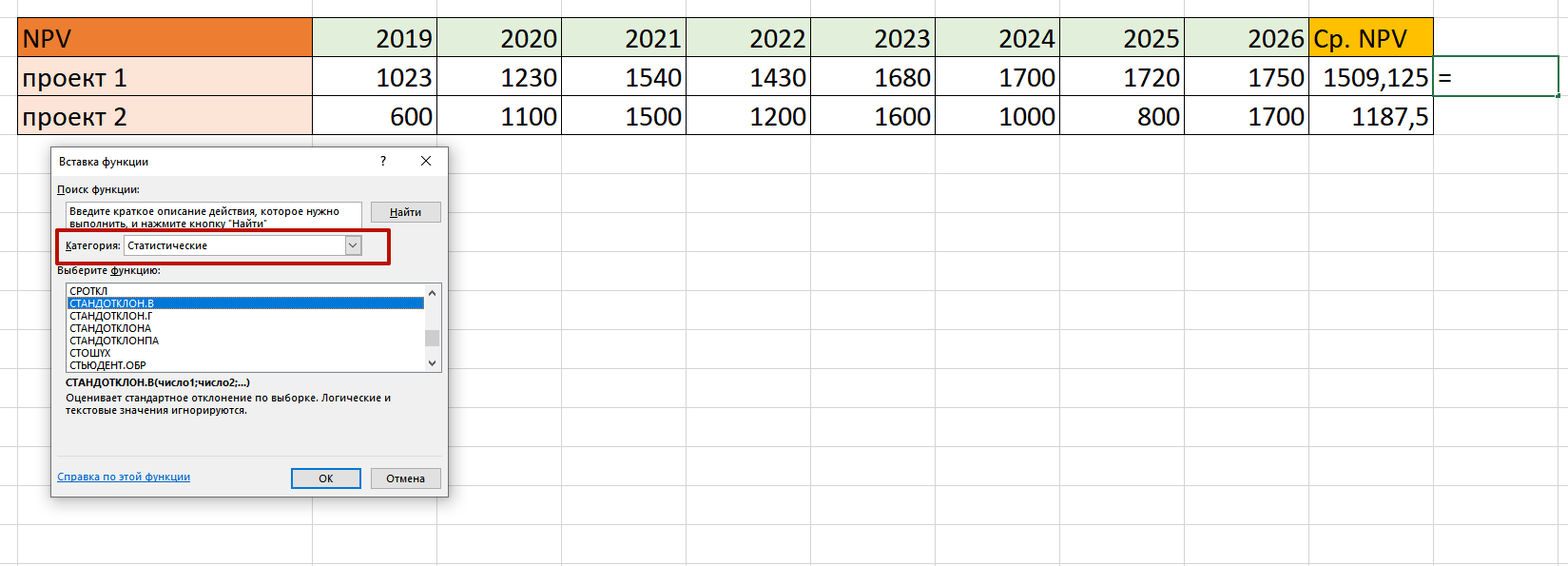
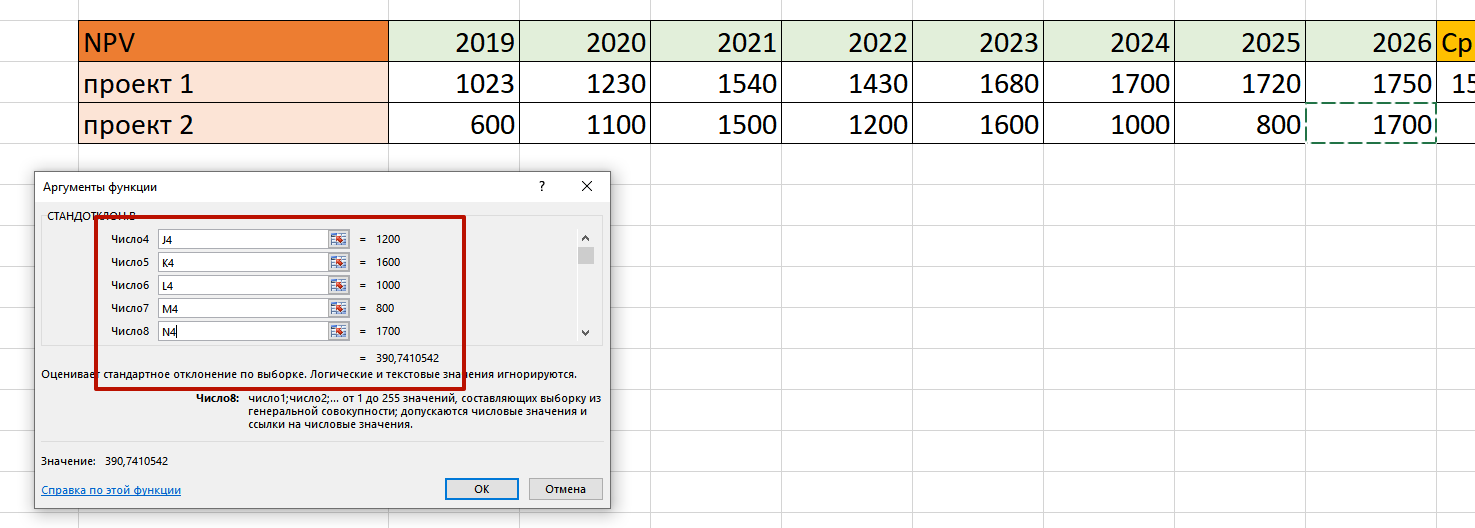
Теперь необходимо вычислить среднеквадратичное отклонение. Для этого предназначена функция СТАНДОТКЛОН.В
Обратите внимание, что в любую строку необходимо вбить одну ячейку, а не выбирать весь диапазон:
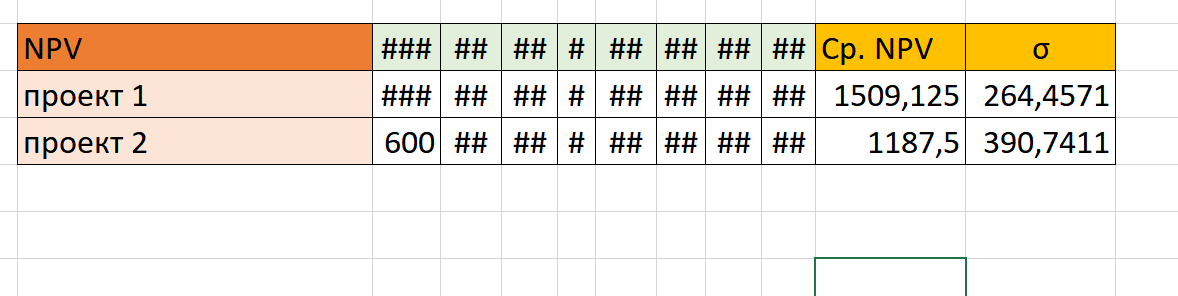
Таким образом, у нас есть рассчитанные посредственные значения доходности и среднеквадратичного отклонения по двум проектам:
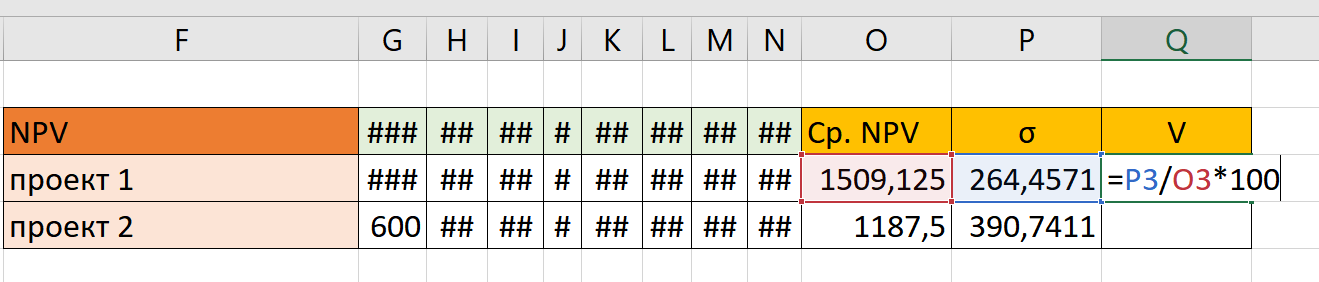
Теперь нам нужно найти коэффициент вариации. Для этого мы попросту вписываем вручную формулу: ячейку σ делим на среднюю доходность и умножаем на 100:
Таким образом, получаем следующие смыслы коэффициента вариации:
Можно сделать вывод о том, что первый проект менее рисковый, чем второй.