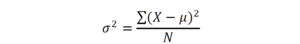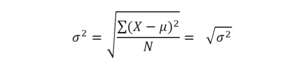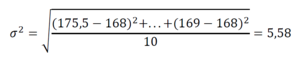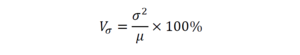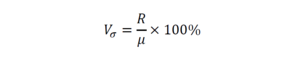Что показывает коэффициент вариации простыми словами
Коэффициент вариации в статистике: примеры расчета

Показатели описательной статистики
Существует несколько показателей, которые использует описательная статистика.
Среднее арифметическое
Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):
168, 171, 175, 177, 179, 187, 174, 176, 179, 169.
Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:
Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться. Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического. Если обратиться к росту студентов, то формула будет выглядеть следующим образом:
Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)
Если свести все к строгим математическим терминам, то определение среднего арифметического (обозначается греческой буквой – μ («мю»)) будет звучать так:
Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).
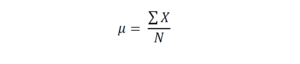
Стандартное отклонение
Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.
На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:
Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:
Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:
Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.
Коэффициент вариации
Среднее квадратичное отклонение хорошо работает с рядами, в которых разброс значений не очень велик (это хорошо прослеживалось на примере роста, где интервал был всего 18 см). Если бы ряд наших измерений был значительнее, а варьирование роста было сильнее, то стандартное отклонение стало непоказательным и нам потребовался бы критерий, который может отразить разброс в относительных единицах (т. е. в процентах, относительно средней величины).
Для этих целей предусмотрены абсолютные и относительные показатели вариации в статистике, характеризующие вариационные масштабы:
Квадратический коэффициент вариации (обозначается как Vσ) – это отношение среднеквадратичного отклонения к среднеарифметическому значению, выраженное в процентах.
Для нашего примера со студентами, определить Vσ несложно — он будет равен 3,18%. Основная закономерность – чем больше будет изменяться значение коэффициента, тем больше разброс вокруг среднего значения и тем менее однородна выборка.
Преимущество коэффициента вариации в том, что он показывает однородность значений (асимметрия) в ряду наших измерений, кроме того, на него не оказывают влияния масштаб и единицы измерения. Эти факторы делают коэффициент вариации особенно популярным в биомедицинских исследованиях. Будет считаться, что эксцесс значения Vσ =33% отделяет однородные выборки от неоднородных.
Если найти в ряду значений роста (первый пример) максимальное и минимальное значения, то получим размах вариации (обозначается как R, иногда ещё называется колеблемостью). В нашем примере – это значение будет равно 18 см. Эта характеристика используется для расчёта коэффициента осцилляции:
Коэффициент осцилляции – показывает как размах вариации будет относиться к среднему арифметическому ряда в процентном отношении.
Расчёты в Microsoft Ecxel 2016
Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:
| Наименование показателя | Расчёт в Excel 2016* |
| Среднее арифметическое | =СРГАРМ(A1:A10) |
| Дисперсия | =ДИСП.В(A1:A10) |
| Среднеквадратический показатель | =СТАНДОТКЛОН.В(A1:A10) |
| Коэффициент вариации | =СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10) |
| Коэффициент осцилляции | =(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10) |
* в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.
Итак, обобщим информацию:
Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила коэффициент вариации, который является мерой однородности данных.
Коэффициент вариации (CV)
Коэффициент вариации (coefficient of variation, CV) — это статистическая мера дисперсии (разброса) данных вокруг некоторого среднего значения. Коэффициент вариации представляет собой отношение среднеквадратичного отклонения к среднему значению и является весьма полезной величиной для сравнения степени вариации при переходе от одного ряда данных к другому, даже если их средние значения резко отличаются друг от друга.
Понимание коэффициента вариации
Коэффициент вариации показывает степень изменчивости некоторой выборки данных по отношению к среднему их значению. В финансах данный коэффициент позволяет инвесторам определить, насколько велика волатильность, или риск, по сравнению с величиной ожидаемой прибыли от инвестиций.
Чем меньше значение CV, тем лучший компромисс наблюдается между риском и доходностью. Обратите внимание, что если ожидаемая доходность в знаменателе отрицательна или равна нулю, полученное значение коэффициента может ввести вас в заблуждение.
Коэффициент вариации может быть весьма полезен при использовании соотношения риск/прибыль для выбора объекта инвестиций. Например, инвестор не склонный к риску будет рассматривать активы с исторически низкой степенью волатильности и высокой степенью доходности по отношению к общему рынку (или к отдельной отрасли). И наоборот, инвесторы склонные к риску, будут стремиться инвестировать в активы с исторически высокой степенью волатильности.
Формула CV может использоваться для определения дисперсии между исторической средней ценой и текущими показателями цены акции, товара или облигации.
Обычно данный коэффициент используют в таких целях как:
КЛЮЧЕВЫЕ МОМЕНТЫ
Формула CV
Ниже приведена формула для расчета коэффициента вариации:
Обратите внимание, что если значение ожидаемой доходности в знаменателе формулы коэффициента вариации отрицательна или равна нулю, то результат расчёта по ней нельзя считать корректным.
Коэффициент вариации в Excel и Open Office
Коэффициент вариации можно достаточно легко рассчитать в Excel. Несмотря на то, что в нём нет стандартной функции для расчёта CV, но зато есть функции позволяющие рассчитать стандартное отклонение (СТАНДОТКЛОН) и среднее значение (СРЗНАЧ). Сначала используйте функцию стандартного отклонения, затем вычислите среднее значение, а после этого разделите ячейку, содержащую стандартное отклонение, на ячейку содержащую среднее значение.
В Open Office данный показатель рассчитывается аналогично. Функция стандартного отклонения здесь — STDEV, а функция среднего значения — AVERAGE.
Давайте рассмотрим пример расчёта коэффициента вариации в Open Office. Предположим, что у нас есть три потенциальных объекта для инвестиций — объект А, объект Б и объект В. Прибыль по каждому из этих проектов за последние 6 лет занесена в таблицу представленную ниже:
Давайте рассчитаем значение CV для каждого из этих объектов. Начнём с расчёта стандартных отклонений. Для этого применим к ряду значений прибыли отдельно по каждому объекту функцию STDEV:
Аналогичным образом рассчитаем среднее значение для каждого ряда данных:
Наконец рассчитаем CV. Для этого разделим полученные значения отклонений на средние значения. В результате получим следующую таблицу:
Кликните по картинке для увеличения
Очевидно, что из всех представленных объектов инвестиций предпочтительным будет объект Б имеющий наименьшее значение коэффициента CV.
Пример использования коэффициента вариации для выбора объекта инвестиций
Рассмотрим инвестора не склонного к риску, который хочет инвестировать в биржевой фонд (ETF) состоящий из корзины ценных бумаг отслеживающей индекс широкого рынка. Инвестор выбирает SPDR S&P 500 ETF, Invesco QQQ ETF и iShares Russell 2000 ETF. Затем он анализирует доходность и волатильность выбранных ETF за последние 15 лет и предполагает, что в будущем они могут иметь аналогичную доходность в отношении к своим долгосрочным средним значениям.
Для принятия решения инвестором используется следующая 15-летняя историческая информация:
Исходя из этих данных, инвестор может инвестировать либо в SPDR S&P 500 ETF, либо в iShares Russell 2000 ETF, так как соотношение риска и вознаграждения для них является сравнительно одинаковым. А для Invesco QQQ ETF соотношение риск-доходность, как видите, будет несколько хуже.
Коэффициент вариации | Coefficient of Variation, CV
В статистике коэффициент вариации (англ. Coefficient of Variation, CV) используется для сравнения рассеивания двух случайных величин, имеющих разные единицы измерения, относительно ожидаемого значения, что позволяет получить сопоставимые результаты. В портфельной теории этот показатель используется в качестве относительной меры риска, связанного с инвестированием в определенный актив или портфель активов. Коэффициент вариации особенно полезен в ситуации, когда два актива имеют разную ожидаемую доходность и разный уровень риска (среднеквадратическое отклонение). Например, одна инвестиция может характеризоваться более высокой ожидаемой доходностью, а другая более низким среднеквадратическим отклонением.
Формула
Коэффициент вариации является отношением среднеквадратического отклонения случайной величины к ее ожидаемому значению, для чего необходимо использовать следующую формулу:
σ – среднеквадратическое отклонение случайной величины;

Интерпретация
Коэффициент вариации является относительной мерой риска, в отличие от дисперсии и среднеквадратического отклонения, поэтому позволяет сопоставлять риск и доходность двух и более активов, которые могут существенно отличаться. Другими словами, этот показатель увязывает среднеквадратическое отклонение с ожидаемой доходностью актива, что дает возможность оценить соотношение риск/доходность в относительном выражении, что позволяет обеспечить сопоставимость полученных результатов.
Следует отметить, что когда ожидаемая доходность ценной бумаги близка к 0, то значение коэффициента вариации может быть очень большим. Поэтому незначительное изменение ожидаемой доходности ценной бумаге может приводить к значительному изменению этого показателя, что необходимо учитывать при обосновании инвестиционных решений.
Пример расчета
Финансовый аналитик должен обосновать включение в портфель дополнительной ценной бумаги, выбрав из двух ценных бумаг, историческая доходность которых за последние пять лет представлена в таблице.
Ожидаемая доходность акций Компании А составит 13,646%, а Компании Б 15,608%.


При этом среднеквадратическое отклонение доходности для акций Компании А составляет 4,236%, а акций Компании Б 7,284%. (Как рассчитывается среднеквадратическое отклонение можно прочитать здесь)
В этом примере акции одновременно обладают разной ожидаемой доходностью и разным уровнем риска. При этом одна из них характеризуется более высокой ожидаемой доходностью, а другая более низким уровнем риска. Чтобы сопоставить эти ценные бумаги необходимо рассчитать коэффициент вариации доходности, который для акций Компании А будет равен 0,31, а для акций Компании Б 0,47.
Итак, ожидаемая доходность акций Компании Б превышает доходность акций Компании А в 1,144 раза (15,608/13,646), однако и риск инвестирования в них больше в 1,516 раза (0,47/0,31). Следовательно, акции Компании А являются более предпочтительными для включения в портфель, поскольку обладают лучшим соотношением риск/доходность.
Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Коэффициент вариации: для чего нужен, расчет, примеры, упражнения
Содержание:
В коэффициент вариации (CV) выражает стандартное отклонение относительно среднего. То есть он пытается объяснить, насколько велико значение стандартного отклонения по отношению к среднему.
Например, переменный рост четвероклассников имеет коэффициент вариации 12%, что означает, что стандартное отклонение составляет 12% от среднего значения.
Обозначается CV, коэффициент вариации является безразмерным и получается делением стандартного отклонения на среднее значение и умножением на сто.
Чем меньше коэффициент вариации, тем меньше отклонение данных от среднего. Например, в переменной со средним значением 10 и другой со средним значением 25, обе со стандартным отклонением 5, их коэффициенты вариации составляют 50% и 20% соответственно. Конечно, первая переменная более изменчива (дисперсия), чем вторая.
Рекомендуется работать с коэффициентом вариации для переменных, измеряемых в шкале пропорций, то есть шкалах с абсолютным нулем независимо от единицы измерения. Примером может служить переменная расстояния, которая не имеет значения, измеряется она в ярдах или метрах, ноль ярдов или ноль метров означает одно и то же: нулевое расстояние или смещение.
Для чего нужен коэффициент вариации?
Коэффициент вариации служит для:
— Коэффициент вариации часто используется как показатель надежности в научных экспериментах. Говорят, что если коэффициент вариации составляет 30% или больше, результаты эксперимента следует отбросить из-за их низкой надежности.
— Это позволяет предсказать, насколько сгруппированы вокруг среднего значения изучаемой переменной, даже не зная ее распределения. Это очень помогает при оценке ошибок и вычислении размеров выборки.
Предположим, что переменные вес и рост людей измеряются в совокупности. Вес с CV 5% и рост с CV 14%. Если вы хотите взять выборку из этой совокупности, размер выборки должен быть больше для оценок роста, чем для веса, поскольку существует большая вариативность в измерении роста, чем в измерении веса.
Важное наблюдение за полезностью коэффициента вариации заключается в том, что он теряет смысл, когда значение среднего близко к нулю. Среднее значение является делителем вычисления CV, и, следовательно, очень маленькие его значения приводят к тому, что значения CV будут очень большими и, возможно, не поддающимися вычислению.
Как рассчитывается?
Расчет коэффициента вариации относительно прост, достаточно знать среднее арифметическое и стандартное отклонение набора данных, чтобы рассчитать его по формуле:
Если они неизвестны, но данные доступны, можно предварительно рассчитать среднее арифметическое и стандартное отклонение, используя следующие формулы:
Примеры
Пример 1
Были измерены веса в кг группы из 6 человек: 45, 62, 38, 55, 48, 52. Мы хотим знать коэффициент вариации переменной веса.
Он начинается с вычисления среднего арифметического и стандартного отклонения:
Ответ: коэффициент вариации переменного веса 6 человек в выборке составляет 16,64%, при среднем весе 50 кг и стандартном отклонении 8,32 кг.
Пример 2
В отделении неотложной помощи больницы измеряют температуру тела в градусах Цельсия у 5 детей, находящихся на лечении. Результаты 39-е, 38-е, 40-е, 38-е и 40-е. Какой коэффициент вариации переменной температуры?
Он начинается с вычисления среднего арифметического и стандартного отклонения:
Теперь он подставляется в формулу для коэффициента вариации:
Ответ: коэффициент вариации температурной переменной для 5 детей в выборке составляет 2,56%, при средней температуре 39 ° C и стандартном отклонении 1 ° C.
Что касается температуры, то следует проявлять осторожность при обращении с весами, поскольку, будучи переменной, измеряемой в интервальной шкале, она не имеет абсолютного нуля. В рассматриваемом случае, что бы произошло, если бы температуры были преобразованы из градусов Цельсия в градусы Фаренгейта:
Рассчитываются среднее арифметическое и стандартное отклонение:
Теперь он подставляется в формулу для коэффициента вариации:
Ответ: коэффициент вариации температурной переменной у 5 детей в выборке составляет 1,76%, при средней температуре 102,2 ° F и стандартном отклонении 1,80 ° F.
Решенные упражнения
Упражнение 1
Вес в кг 10 сотрудников почтового отделения был измерен: 85, 62, 88, 55, 98, 52, 75, 70, 76, 77. Мы хотим знать коэффициент вариации переменной веса.
Рассчитываются среднее арифметическое и стандартное отклонение:
Теперь он подставляется в формулу для коэффициента вариации:
Ответ: коэффициент вариации переменного веса 10 человек в почтовом отделении составляет 19,74%, при среднем весе 73,80 кг и стандартном отклонении 14,57 кг.
Упражнение 2.
В одном городе измеряется рост 9 465 детей во всех школах первого класса, средний рост составляет 109,90 см со стандартным отклонением 13,59 см. Рассчитайте коэффициент вариации.
Ответ: коэффициент вариации переменного роста первоклассников города составляет 12,37%.
Упражнение 3.
Смотритель парка подозревает, что популяции черных и белых кроликов в его парке не имеют одинаковой изменчивости в размерах. Чтобы продемонстрировать это, он взял образцы по 25 кроликов из каждой популяции и получил следующие результаты:
— Белые кролики: средний вес 7,65 кг и стандартное отклонение 2,55 кг.
-Черные кролики: средний вес 6,00 кг и стандартное отклонение 2,43 кг.
Смотритель парка прав? Ответ на гипотезу смотрителя парка можно получить с помощью коэффициента вариации:
Ответ: коэффициент вариации веса черных кроликов почти на 7% больше, чем у белых кроликов, поэтому можно сказать, что смотритель парка прав в своем подозрении, что вариабельность веса двух популяций кроликов не равны.
Ссылки
Эффект кросса: что это такое и как влияет на восприятие
Маркетинг для психологов: команда «Психология и разум» к услугам вашей клиники