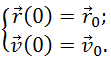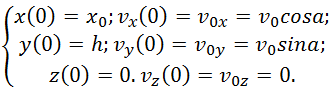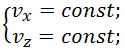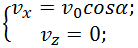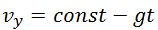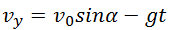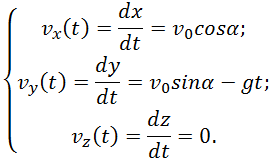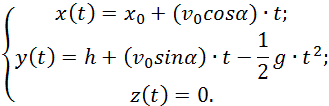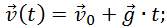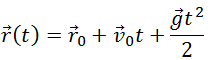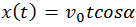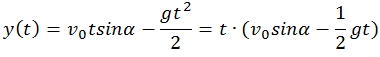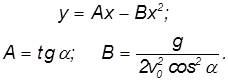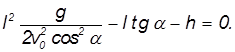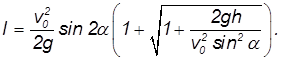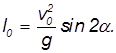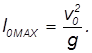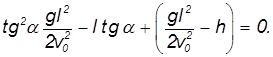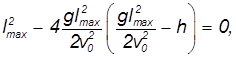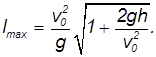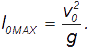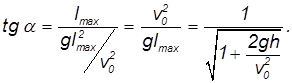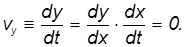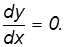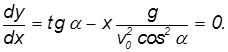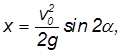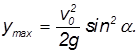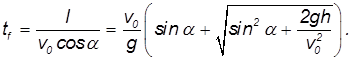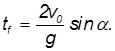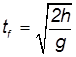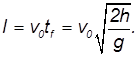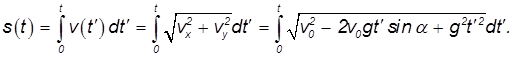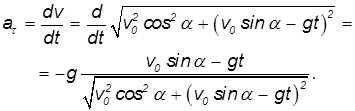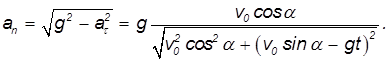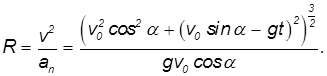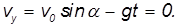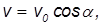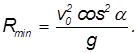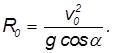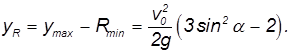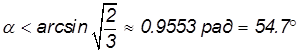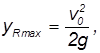Что показывает кривизна траектории
Что показывает кривизна траектории
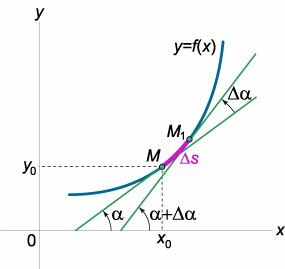
Рассмотрим плоскую кривую, заданную уравнением \(y = f\left( x \right).\) Пусть в точке \(M\left(
Абсолютное значение отношения \(\large\frac<<\Delta \alpha >><<\Delta s>>\normalsize\) называется средней кривизной дуги \(M
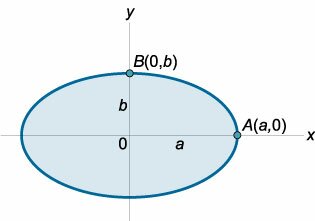
Очевидно, достаточно найти кривизну эллипса в точках \(A\left(
Для расчета кривизны удобно перейти от канонического уравнения эллипса к уравнению в параметрической форме : \[x = a\cos t,\;\;\;y = b\sin t.\] где \(t\) − параметр. В точке \(A\left(
Данная функция достигает максимума в точках \(x = \large\frac<<2\pi n>>
В данном случае точка \(x = 0\) является точкой перегиба функции \(y = \arctan x.\) Поскольку в точке перегиба вторая производная равна нулю, то кривизна здесь также должна быть равна нулю, что и показывает полученное решение.
Экспоненциальная функция \(y =
Радиус кривизны плоской кривой
Любая линия является кривой, даже прямая. Поэтому к любой линии применимы такие характеристики как кривизна или радиус кривизны. Как правило кривизна обозначается латинской литерой k, а радиус кривизны греческой литерой ρ.
Между собой эти характеристики кривой связаны следующим образом:
k = 1/ρ (542.1)
Т.е. чем больше радиус кривой, тем меньше ее кривизна.
А теперь рассмотрим несколько частных случаев кривых.
Радиус кривизны окружности
Как определить радиус окружности, мы рассмотрим ниже.
Кривизна дуги
На рисунке 542.1 мы видим дугу АВ, показанную оранжевым цветом, являющуюся частью окружности с радиусом R. Кроме того, мы видим, что угол α, образованный радиусами в точках А и В, равен углу между касательными (показаны фиолетовым цветом) к окружности в этих точках.
Эти закономерности позволяют определить радиус дуги и найти центр окружности даже тогда, когда изначально мы окружность не видим, а только имеем дугу.
Понятие кривизны дуги формулируется так:
Т.е. зная длину дуги m и угол α между касательными, мы можем определить кривизну дуги:
А так как длина дуги зависит от угла между радиусами или между касательными в концах дуги:
то, подставив значение длины дуги в уравнение (542.3), получим:
Примечание: При измерении угла между касательными не в радианах, а в градусах уравнение длины дуги имеет другой вид:
но сути дела это не меняет. Такая запись по-прежнему означает, что мы рассматриваем часть длины окружности. Так при α = 360° дуга становится окружностью
Более того, сама идея радианов на этой формуле и основана, так прямой угол 90° = П/2, развернутый 180° = П и т.д.
Рисунок 542.2. Дуга из точки начала координат.
Радиус кривизны прямой линии
Любая прямая линия, даже бесконечно длинная, может рассматриваться как бесконечно малая часть окружности, т.е. как дуга. Соответственно в каких единицах измерять радиус такой окружности даже трудно представить.
Поэтому обычно прямой линией называют кривую с бесконечно большим радиусом:
kп.л = 1/∞ = 0 (542.6)
все линии, которые в одной из плоскостей имеют бесконечно большой радиус кривизны, считаются плоскими
Ну и на закуску еще несколько парадоксов, на этот раз связанных с определениями кривизны и радиуса:
1. Из уравнения (542.1) можно сделать вывод, что:
kp = 1 (542.7)
Соответственно для прямой линии:
0·∞ = 1 (542.7.2)
Т.е. если бесконечно много раз взять ноль, то на единичку мы наскребем. Впрочем дальше будет еще веселее.
Получается, что параллельные прямые пересекаться не должны, но где-то в бесконечности все-таки пересекаются.
Разрешить этот парадокс пытались многие математики, однако в пределах евклидовой геометрии при принятом толковании определений данный парадокс не разрешим.
Радиус кривизны точки
kт. = 1/0 = ∞ (542.9)
И хотя нас с первых лет обучения в школе учат, что делить на 0 нельзя и даже встроенный в операционную систему калькулятор пишет, что «деление на ноль невозможно», тем не менее делить на ноль можно, а результатом деления всегда будет бесконечность.
Как и в случае с прямой мы имеем парадоксальный результат, выражаемый формулой (542.5.2). Тем не менее точку также можно отнести к плоской кривой, имеющей постоянный радиус кривизны.
Рисунок 541.4. Радиус окружности, как гипотенуза прямоугольного треугольника.
R 2 = x 2 + y 2 (541.1.2)
А в общем случае, когда координаты центра окружности не совпадают с началом координат:
Рисунок 542.3. Окружность, центр которой не совпадает с началом координат.
Плоские кривые с изменяющимся радиусом кривизны
Примеров плоских кривых с изменяющимся радиусом кривизны очень много, это и гиперболы, и параболы, и синусоиды и т.п. Определение радиуса кривизны таких кривых основано на следующих теоретических предпосылках:
1. Любую окружность можно рассматривать как некоторое множество дуг.
2. Если количество дуг, составляющих окружность, стремится к бесконечности, то соответственно длина таких дуг стремится к нулю (m → 0).
3. Если мы обозначим длину такой очень короткой дуги как приращение функции длины окружности (m = Δl), то уравнение кривизны (542.3) примет следующий вид:

4. Тогда любую плоскую кривую с изменяющимся радиусом можно рассматривать как стремящееся к бесконечности множество дуг с постоянным радиусом. Другими словами в пределах любой кривой, описываемой параметрическими уравнениями, всегда можно выделить дугу, пусть даже и очень малой длины, стремящейся к точке и определить для нее кривизну и радиус кривизны в рассматриваемой точке.

Соответственно кривизна плоской кривой в рассматриваемой точке будет равна:

k = y» = d 2 y/dx 2 (542.12.2)
Т.е. формально в таких случаях кривизной считается не отношение угла наклона между касательными к длине дуги, а некоторая величина, примерно соответствующая высоте h на рисунке 542.2.
Эта особенность второй производной очень активно используется в частности для упрощения определения прогиба элементов строительных конструкций.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Траектория
Из Википедии — свободной энциклопедии
Траекто́рия материа́льной то́чки — линия в пространстве, по которой движется тело, и представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта. [1] Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения.
Кроме того, и при наличии движущегося по ней объекта, траектория, изображаемая в наперёд заданной системе пространственных координат, сама по себе не может ничего определённого сказать в отношении причин его движения, пока не проведён анализ конфигурации поля действующих на него сил в той же координатной системе. [2]
Не менее существенно, что форма траектории неотрывно связана и зависит от конкретной системы отсчёта, в которой описывается движение. [3]
Возможно наблюдение траектории при неподвижности объекта, но при движении системы отсчёта. Так, звёздное небо может послужить хорошей моделью инерциальной и неподвижной системы отсчёта. Однако при длительной экспозиции эти звёзды представляются движущимися по круговым траекториям (Рис. 3)
Возможен и случай, когда тело явно движется, но траектория в проекции на плоскость наблюдения является одной неподвижной точкой. Это, например, случай летящей прямо в глаз наблюдателя пули или уходящего от него поезда.
2.7. Движение тела, брошенного под углом к горизонту
Рис. 2.16. Движение тела, брошенного под углом к горизонту
Вывод уравнений движения материальной точки в поле силы тяжести
Напишем уравнение движения (уравнение второго закона Ньютона):
Как уже было сказано, мы учитываем только силу тяжести 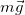
Масса тела в уравнении движения сокращается
это означает, что тела — материальные точки — любых масс при одних и тех же начальных условиях будут двигаться в однородном поле тяжести одинаково. Спроектируем уравнение (2.7.2) на оси декартовой системы координат. Горизонтальная ось ОХ показана на рис. 13 пунктиром, ось OY проведем через точку О вертикально вверх, а горизонтальную ось OZ, также проходящую через точку О, направим перпендикулярно вектору 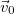
Вертикальным направлением, по определению, называется направление вектора 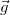
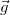
Рис. 2.17. Движение тела, брошенного под углом к горизонту.
Добавим к уравнениям движения начальные условия, которые определяют положение и скорость тела в начальный момент времени t0, пусть t0 = 0. Тогда, согласно рис. 2.7.4
Или в проекциях на оси координат:
Если производная некоторой функции равна нулю, то функция постоянна, соответственно из первого и третьего уравнений (2.7.3) получаем:
Константы находятся из начальных условий, а именно: из первого и третьего уравнений (2.7.5) следует, что в любой момент времени
Во втором уравнении (2.7.3) производная равна константе, откуда следует, что функция зависит от своего аргумента линейно, то есть
Эта константа также находится из начальных условий. Подставляя в (2.7.8) t = 0 и сравнивая результат (vy(0) = const) cо вторым уравнением в (2.7.5) получаем
Объединяя (2.7.7) и (2.7.9), получаем окончательные выражения для зависимостей проекций скорости на оси координат от времени:
Для определения зависимостей от времени координат тела необходимо выполнить еще одно интегрирование — проинтегрировать по времени уравнения (2.7.10) с учетом начальных условий (2.7.5). Используя ту же логику: если производная равна нулю, то функция постоянна, если производная постоянна, то функция зависит от своего аргумента линейно, и подбирая константы так, чтобы удовлетворить начальные условия, можно получить следующий результат:
Третье уравнение (2.7.11) показывает, что траектория тела плоская, целиком лежит в плоскости XOY, это вертикальная плоскость, определяемая векторами 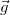
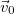
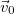
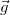
Если три уравнения (2.7.10) умножить на орты осей 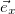
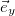

Формулы (2.7.12) и (2.7.13) можно было получить сразу, непосредственно из (2.7.2), если учесть, что ускорение свободного падения есть 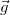
Из (2.7.13) в частности видно, что радиус-вектор является суммой трех векторов, складывающихся по обычным правилам, что наглядно показано на рис. 2.18.
Рис. 2.18. Представление радиус-вектора r(t) в произвольный момент времени t в виде суммы трех векторов
Эти векторы представляют собой:
Здесь отчетливо проявляется принцип независимости движений, известный в других областях физики как принцип суперпозиции (наложения). Вообще говоря, согласно принципу суперпозиции результирующий эффект нескольких воздействий представляет собой сумму эффектов от каждого воздействия в отдельности. Он является следствием линейности уравнений движения.
Видео 2.3. Независимость горизонтального и вертикального перемещений при движении в поле тяжести.
Поместим начало отсчета в точку бросания. Теперь 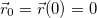
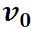
Рис. 2.19. Проекции начальной скорости на координатные оси
Спроецируем 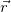
Траектория полета. Если из системы полученных уравнений исключить время t, то получим уравнение траектории:
Это уравнение параболы, ветви которой направлены вниз.
Дальность полета при стрельбе с высоты h. В момент падения тела 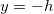
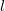
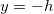
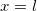
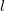
У квадратного уравнения имеется два решения (в данном случае — положительное и отрицательное). Нам нужно положительное решение. Стандартное выражение для корня квадратного уравнения нашей задачи может быть приведено к виду:
При 
Из нее следует, в частности, что максимальная дальность полета
достигается при 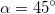
Максимальная дальность полета. При выстреле с горы высотой 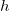
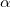
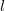
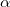
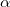
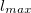
Обратимся снова к квадратному уравнению относительности дальности полета 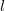

перепишем его в виде:
Мы снова получили квадратное уравнение, на этот раз — для неизвестной величины 
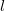
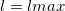
откуда следует результат
При 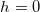
Обычно высота 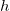
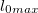
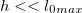
то есть дальность выстрела увеличивается примерно на высоту подъема пушки.
Когда l = lmax, и a = amax, как уже отмечалось, дискриминант квадратного уравнения равен нулю, соответственно, его решение имеет вид:
Поскольку тангенс меньше единицы, угол, при котором достигается максимальная дальность полета, меньше 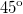
Максимальная высота подъёма над начальной точкой. Эта величина может быть определена из равенства нулю вертикальной составляющей скорости в верхней точке траектории
При этом горизонтальная составляющая скорости 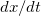
Дифференцируя ранее полученное уравнение траектории, приходим к уравнению:
что при подстановке в уравнение траектории полета приводит к формуле:
Продолжительность полета. Поскольку горизонтальная составляющая скорости не меняется, то продолжительность полета 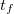
При 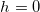
При 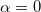
равно времени падения тела с высоты 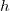
Путь, пройденный телом. За время t тело проходит путь
Интеграл берется в элементарных функциях, но из-за громоздкости ответа мы не выписываем здесь соответствующее выражение.
Расстояние от места выстрела. К моменту времени t расстояние от места выстрела определяется модулем радиус-вектора:
Радиус кривизны траектории в заданной точке. В отсутствие сопротивления воздуха тело движется с постоянным ускорением силы тяжести 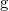
Тангенциальная компонента ускорения, характеризующая быстроту изменения модуля скорости, равна
Нормальная компонента ускорения, изменяющая направление скорости тела, определяется соотношением:
Используя связь нормальной компоненты ускорения с радиусом кривизны, находим 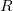
В числителе этого выражения в степени 3/2 стоит модуль скорости. Поэтому, даже не вычисляя производной, мы можем ответить на вопрос, в какой точке траектории кривизна максимальна, а радиус кривизны C = 1/R минимален. Радиус кривизны R достигает минимума там, где минимальна скорость, а это имеет место в верхней точке траектории, в которой вертикальная компонента скорости равна нулю:
Еще раз напомним, что горизонтальная компонента скорости, всюду имеет одно и то же значение. В верхней точке модуль скорости равен горизонтальной составляющей скорости
Для сравнения: радиус кривизны 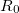
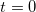
Положение центра кривизны (для высшей точки траектории). По определению радиуса кривизны центр кривизны для высшей точки траектории находится прямо под этой точкой на высоте
Напомним, что мы отсчитываем вертикальные расстояния от уровня пушки, а не от уровня моря.
эта координата отрицательна, то есть центр кривизны находится ниже пушки. Максимально высокое положение центр кривизны занимает при 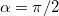
что совпадает с верхней точкой траектории. Тогда радиус кривизны равен нулю. Это значит, что кривизна в этой точке бесконечна, в чем легко убедиться, представив себе траекторию при вертикальном движении снаряда.






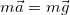
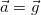
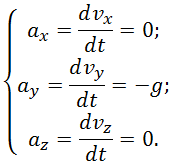
.png)