Что показывает модуль вектора

Модуль вектора. Длина вектора.

Определение длины вектора

Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.

Формулы длины вектора

Формула длины вектора для плоских задач

В случае плоской задачи модуль вектора a = < a_x ; a_y > можно найти воспользовавшись следующей формулой:

Формула длины вектора для пространственных задач

В случае пространственной задачи модуль вектора a = < a_x ; a_y ; a_z > можно найти воспользовавшись следующей формулой:

Примеры задач на вычисление длины вектора

Примеры вычисления длины вектора для плоских задачи

Решение: | a | = √ 3 2 + (-4) 2 = √ 9 + 16 = √ 25 = 5.

Примеры вычисления длины вектора для пространственных задачи

Решение: | a | = √ 2 2 + 4 2 + 4 2 = √ 4 + 16 + 16 = √ 36 = 6.

Примеры вычисления длины вектора для пространств с размерностью большей 3

Решение: | a | = √ 1 2 + (-3) 2 + 3 2 + (-1) 2 = √ 1 + 9 + 9 + 1 = √ 20 = 2√ 5

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Вопросы.

Прямолинейное равноускоренное движение относится к неравномерному движению, т.к. оно происходит с переменной (меняющейся во времени по величине и направлению) скоростью.

2. Что понимают под мгновенной скоростью неравномерного движения?

Под мгновенной скоростью неравномерного движения понимают скорость в конкретной точки траектории в данный момент времени.

3. Что называется ускорением равноускоренного движения?

4. Что такое равноускоренное движение?

Движение с постоянным ускорением называется равноускоренным движением.

5. Что показывает модуль вектора ускорения?

6. Что является единицей ускорения?

В СИ за единицу ускорения принимается ускорение такого равноускоренного движения, при котором за 1 секунду скорость тела изменяется на 1 м/с, т.е 1 м/с 2 (метр на секунду в квадрате или другими словами 1 метр в секунду за секунду).

7. При каком условии модуль вектора скорости движущегося тела увеличивается? уменьшается?

1. За один и тот же промежуток времени модуль вектора скорости первого автомобиля изменился от v₁ до v´, а второго- от v₂ до v´ (скорости изображены в одинаковом масштабе на рисунке 9). Какой из автомобилей двигался в указанный промежуток с большим ускорением? Скорость какого из них возрастала быстрее?

Из рисунка видно, что скорость первого автомобиля возрастала быстрее чем второго, а следовательно у него было большее ускорение.

2. Самолёт, разгоняясь перед взлётом, в течение некоторого промежутка времени двигался равноускоренно. Каково было при этом ускорение самолёта, если за 30 с его скорость возросла от 10 до 55 м/с?

3. С каким ускорением двигался поезд на некотором участке пути, если за 12 с его скорость возросла на 6 м/с?

Источник

Модуль вектора

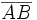
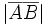
Модулем (длиной) вектора называется длина(норма) соответствующего вектора AB и обозначается как .

Вектор, модуль которого равен 1, называется единичным вектором или ортом.

Смотреть что такое «Модуль вектора» в других словарях:

модуль вектора — величина вектора — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы величина вектора EN absolute value of a vector … Справочник технического переводчика

модуль вектора — vektoriaus modulis statusas T sritis fizika atitikmenys: angl. absolute value of vector vok. Vektorbetrag, m rus. длина вектора, f; модуль вектора, m pranc. module d’un vecteur, m … Fizikos terminų žodynas

Модуль — (от лат. modulus «маленькая мера»): В Викисловаре есть статья «модуль» Мо … Википедия

Модуль (значения) — Модуль (от лат. modulus «маленькая мера») составная часть, отделимая или хотя бы мысленно выделяемая из общего. Модульной обычно называют вещь, состоящую из чётко выраженных частей, которые нередко можно убирать или добавлять, не разрушая вещь… … Википедия

Модуль числа — Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия

модуль волнового вектора — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN magnitude of propagation vector … Справочник технического переводчика

модуль конвольвера кодового вектора огибающей — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN shape codevector convolution module … Справочник технического переводчика

Модуль (в математике) — Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия

МОДУЛЬ — абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… … Математическая энциклопедия

Источник

Характеристики вектора: длина, направление, координаты

У любого вектора есть 2 главные характеристики:

Третья характеристика вектора – это его координаты.

Примечание:

Зная координаты вектора, можно найти его длину и направление. Поэтому, задавать информацию о векторе можно двояко: либо указав его длину и направление, либо его координаты.

Что такое координаты вектора

Координаты вектора – это длины его теней на осях координат (его проекции на оси).

Координаты вектора указывают так:

\( a_ \) – это «x» координата вектора, проекция вектора \( \vec \) на ось Ox;

\( a_ \) — это «y» координата вектора, проекция вектора \( \vec \) на ось Oy;

Координаты вектора можно получить из координат его начальной и конечной точек:

«координата вектора» = «конец» — «начало»

Пример:

\( A \left( 1;1 \right) \) — начальная точка,

\( B \left( 4;3 \right) \) — конечная точка,

\[ \overrightarrow = \left\< AB_; AB_ \right\> \]

\[ \begin AB_ = 4 – 1; AB_ = 3 \\ AB_ = 3 – 1; AB_ = 2 \end \]

Длина вектора (в чем измеряется, как посчитать)

Длину вектора (его модуль) обозначают так:

Как вычислить длину вектора по его координатам

Когда известны координаты вектора, его длину считают так:

\( a_ \) и \( a_ \) — это числа, координаты вектора \( \vec \)

Для двухмерного вектора:

Для трехмерного вектора:

Как вычислить длину вектора с помощью рисунка

Если вектор нарисован на клетчатой бумаге, длину считаем так:

1). Если вектор лежит на линиях клеточек тетради:

— считаем количество клеточек.

Зная масштаб клеток, легко получить длину вектора – умножаем масштаб на количество клеток.

2). Если вектор не лежит вдоль линий:

— проводим вертикаль и горизонталь пунктиром.

\( \Delta x \) — горизонталь; \( \Delta y \) — вертикаль;

— затем применяем формулу:

Как указать направление вектора

Указать направление вектора можно с помощью его координат. Так как в его координатах уже содержится информация о длине и направлении вектора.

Бывает так, что координаты вектора неизвестны, а известна только лишь его длина. Тогда направление можно указать с помощью угла между вектором и какой-либо осью.

Для двумерного вектора

Если вектор двумерный, то для указания направления (см. рис. 10) можно использовать один из двух углов:

Словами указать направление вектора можно так:

Такой способ указания координат используют в полярной системе координат.

Для трехмерного вектора

Когда вектор располагается в трехмерном пространстве, чтобы указать, куда вектор направлен, используют два угла.

Такой способ указания координат используют в сферической системе координат.

Считаем Землю шаром. Расположим ее центр в начале трехмерной системы координат – точке (0 ; 0 ; 0).

Тогда координаты любой точки на поверхности планеты можно указать с помощью радиус-вектора этой точки.

Для указания сферических координат принято использовать:

Источник

Что показывает модуль вектора

1. Основные определения

Вектор пред­ставляет собой направленный отрезок прямой, для которого определены правила (законы) сложения с другими векторами, правило вычитания векторов, правило умножения вектора на число, скалярное произведение двух векторов и некоторые другие операции.

Число, выражающее длину направленного отрезка, называют модулем вектора и обозначают той же буквой, что и сам вектор, но без стрелки наверху, например: модулем вектора `vec v` является число `v`. Часто для обозначения модуля вектора прибегают к помощи знака абсолютной величины и пишут, например, `|vec v|` или `|vec F|`.

Вектор называется нулевым, если его начало и конец совпадают. Нулевой вектор не имеет определённого направления и его длина (модуль) равна нулю.

Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Так, например, на рис. 3 векторы `vec a`, `vec b` и `vec c` коллинеарны.

Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.

В физике точка приложения вектора иногда имеет принципиальное значение. Достаточно вспомнить рычаг: две равные по модулю силы, направленные в одну и ту же сторону, производят на рычаг разное действие, если плечи сил не равны друг другу. И всё же сами силы равны друг другу! Бывают и случаи, когда вектору трудно приписать конкретную точку приложения. Например, если одна система отсчёта движется относительно другой со скоростью `vec v`, то какой точке приписать эту скорость? Всем точкам движущейся системы!

2. Сложение двух векторов.

Пусть даны два произвольных вектора `vec a` и `vec b` (рис. 5а).

Описанное правило есть просто определение суммы векторов. Как и в случае с числами, сумма векторов не зависит от порядка слагаемых, и поэтому можно записать

Оба способа сложения дают идентичный результат и одинаково часто применяются на практике. Когда речь идёт о нахождении суммы трёх и более векторов, часто последовательно используют правило треугольника. Поясним сказанное.

3. Сложение трёх и более векторов.

Пусть нужно сложить три вектора `vec a`, `vec b` и `vec d` (рис. 6).

Для этого по правилу треугольника сначала находится сумма любых двух векторов, например `vec a` и `vec b`, потом полученный вектор `vec c = vec a + vec b` по тому же правилу складывается с третьим вектором `vec d`. Тогда полученный вектор `vec f = vec c + vec d` и будет представлять собой сумму трёх векторов `vec a`, `vec b` и `vec d`: `vec f = vec a + vec b + vec d`. Как и в случае с двумя векторами, порядок слагаемых не влияет на конечный результат.

Так, на рис. 7 вектор `vec g` представляет собой сумму векторов `vec a`, `vec b`, `vec d`, `vec e`, найденную по правилу многоугольника: `vec g = vec a + vec b + vec d + vec e`.

Не всякая векторная сумма может иметь физический смысл. Не всякие величины вообще имеет смысл складывать. Так, например, бессмысленно говорить, что, если у меня температура `36,6^@` и у вас тоже `36,6^@`, то вместе у нас температура `73,2^@`, хотя складывать температуры (числа) никто не запрещает. Всё же чаще всего сумма температур представляет собой никому не нужную величину; она редко входит в какие-либо уравнения (входит почти случайно).

Иное дело – с массой. Если система состоит из тел с массами `m_1`, `m_2`, `m_3` и т. д., то масса всей системы равна `m = m_1 + m_2 + m_3 + ` и т. д. (Если на лифте написано, что максимальный груз, перевозимый лифтом, равен `500` кг, то перед входом в лифт нужно убедиться, что сумма масс вносимых в лифт грузов не превышает `500` кг.) Говорят, что масса – есть аддитивная величина (от английского слова add – добавлять, прибавлять, складывать). А вот температура – не аддитивная величина.

В последнем равенстве мы встречаемся с умножением вектора на скаляр. Поясним эту процедуру.

4. Умножение вектора на скаляр.

Произведением вектора `vec a` на число `k` называют новый вектор `vec b = k vec a`, коллинеарный вектору `vec a`, направленный в ту же сторону, что и вектор `vec a`, если `k > 0`, и в противоположную сторону, если `k

Источник