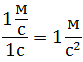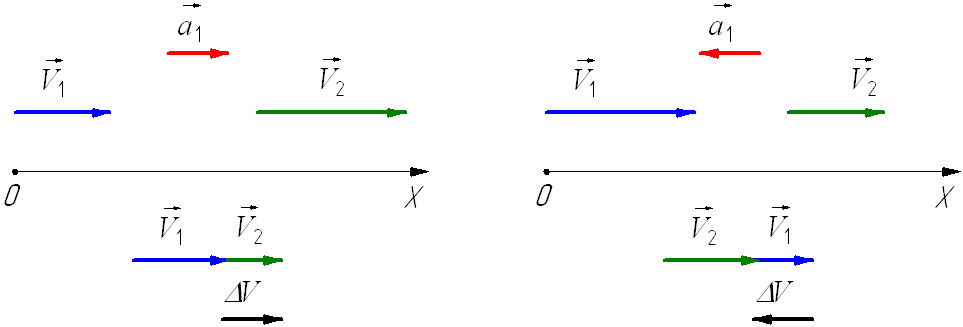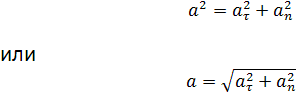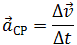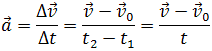Что показывает нормальное ускорение

Ускорение

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).

Среднее ускорение

Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

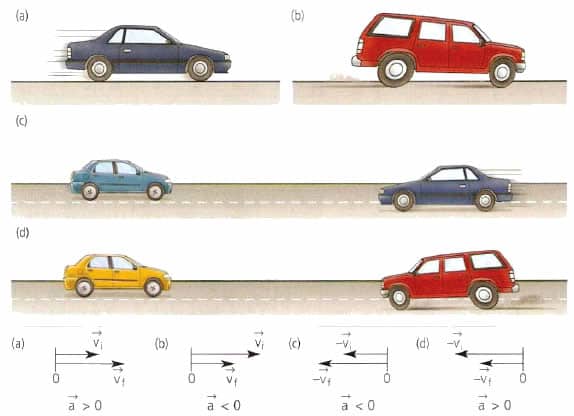
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

а направление вектора ускорения совпадает с вектором скорости

Если скорость тела по модулю уменьшается, то есть

то направление вектора ускорения противоположно направлению вектора скорости 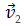Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а

Рис. 1.9. Мгновенное ускорение.

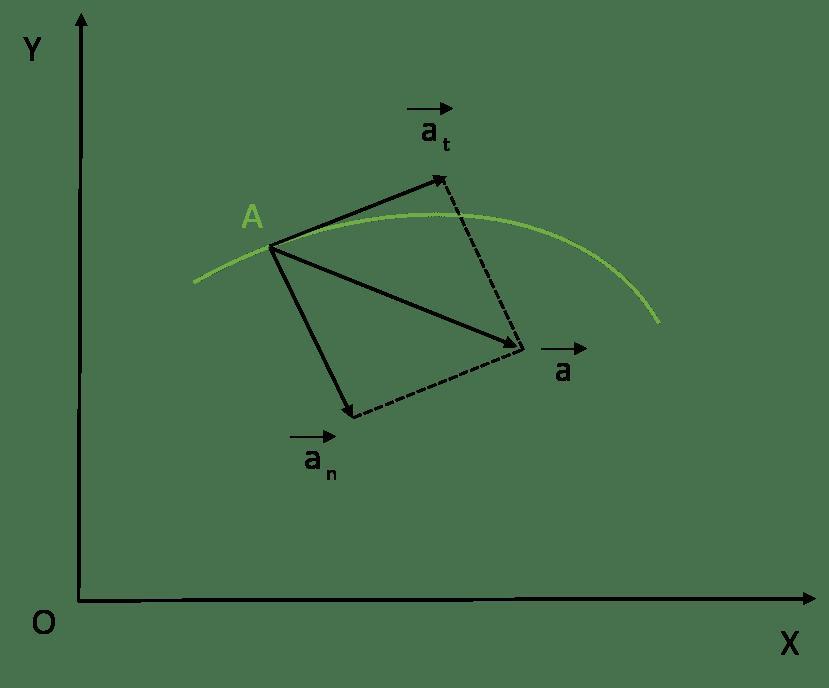
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).

Тангенциальное ускорение

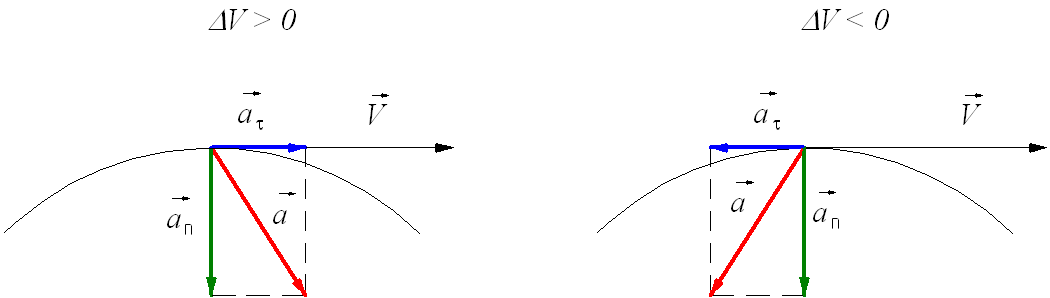
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

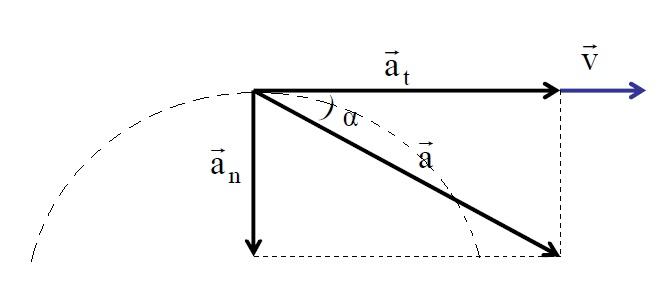
Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения 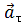(см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 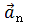Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

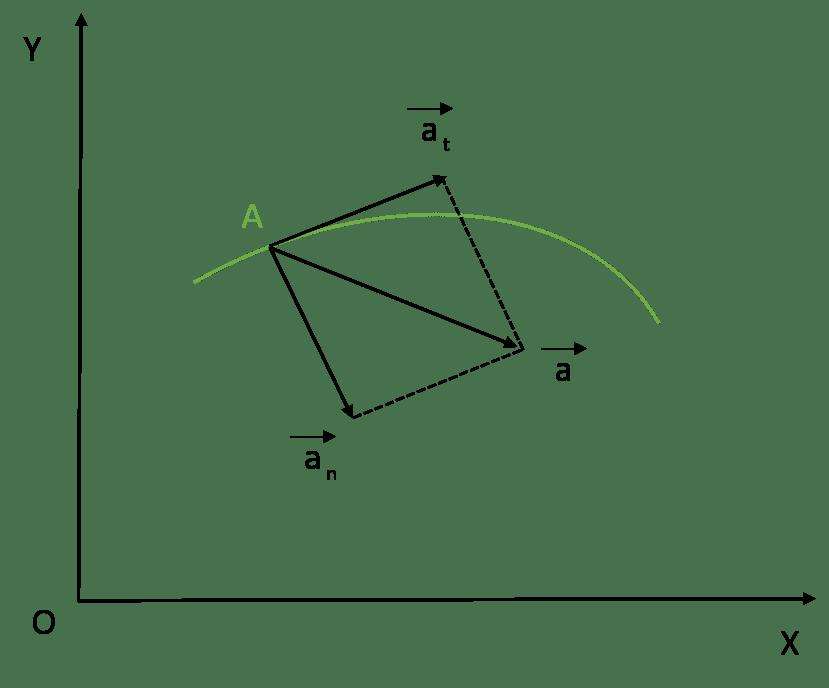
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов:

Источник

Ускорение

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).

Среднее ускорение

Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

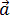
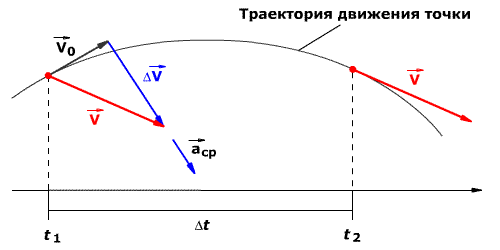
где – вектор ускорения.

Направление вектора ускорения совпадает с направлением изменения скорости Δ = — ₀ (здесь ₀ – это начальная скорость, то есть скорость, с которой тело начало ускоряться).

В момент времени t1 (см. рис 1.8) тело имеет скорость ₀. В момент времени t2 тело имеет скорость . Согласно правилу вычитания векторов найдём вектор изменения скорости Δ = — ₀. Тогда определить ускорение можно так:

Рис. 1.8. Среднее ускорение.

В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

Направление ускорения также совпадает с направлением изменения скорости Δ при очень малых значениях промежутка времени, за который происходит изменение скорости. Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта (проекциями а_Х, a_Y, a_Z).

При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть а направление вектора ускорения совпадает с вектором скорости ₂.

Если скорость тела по модулю уменьшается, то есть то направление вектора ускорения противоположно направлению вектора скорости ₂. Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а

Рис. 1.9. Мгновенное ускорение.

При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).

Тангенциальное ускорение

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения 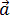_τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 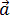_n. Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов:

Источник

Понятие об ускорении. Ускорение тангенциальное, нормальное и полное. Формулы

Каждый, кто знаком с техникой и физикой, знает о понятии ускорения. Тем не менее мало кто знает о том, что эта физическая величина имеет две составляющие: ускорение тангенциальное и ускорение нормальное. Рассмотрим подробнее каждое из них в статье.

Что такое ускорение?

В физике ускорением называют величину, которая описывает быстроту изменения скорости. Причем под этим изменением понимают не только абсолютное значение скорости, но и ее направление. Математически это определение записывают так:

Заметим, что речь идет о производной изменения вектора скорости, а не только ее модуля.

В отличие от скорости, ускорение может принимать как положительные, так и отрицательные значения. Если скорость направлена всегда вдоль касательной к траектории перемещения тел, то ускорение направлено в сторону действующей на тело силы, что следует из второго закона Ньютона:

Ускорение измеряется в метрах в секунду квадратную. Так, 1 м/с2 означает, что скорость на 1 м/с увеличивается за каждую секунду перемещения.

Прямолинейная и криволинейная траектории движения и ускорение

Окружающие нас объекты могут двигаться либо по прямой линии, либо по кривой траектории, например, по окружности.

В случае движения по прямой скорость тела изменяет только свой модуль, но сохраняет направление. Это означает, что полное ускорение может быть вычислено так:

Отметим, что мы опустили значки вектора над скоростью и ускорением. Поскольку полное ускорение направлено по касательной к прямолинейной траектории, то оно называется тангенциальным или касательным. Эта составляющая ускорения описывает исключительно изменение абсолютной величины скорости.

Теперь предположим, что тело совершает движение по криволинейной траектории. В этом случае его скорость можно представить в виде:

a¯ = dv¯/dt = d(v*u¯)/dt = dv/dt*u¯ + v*du¯/dt.

Это и есть исходная формула нормального, тангенциального и полного ускорения. Как видно, равенство в правой части состоит из двух слагаемых. Второе из них отлично от нуля только при криволинейном перемещении.

Формулы тангенциального ускорения и нормального ускорения

Формула для касательной компоненты полного ускорения уже была приведена выше, запишем ее еще раз:

Формула показывает, что тангенциальное ускорение не зависит от того, куда направлен вектор скорости, и меняется ли он во времени. Оно определяется исключительно изменением абсолютного значения v.

Несложно показать геометрически, что эта формула может быть упрощена до такого вида:

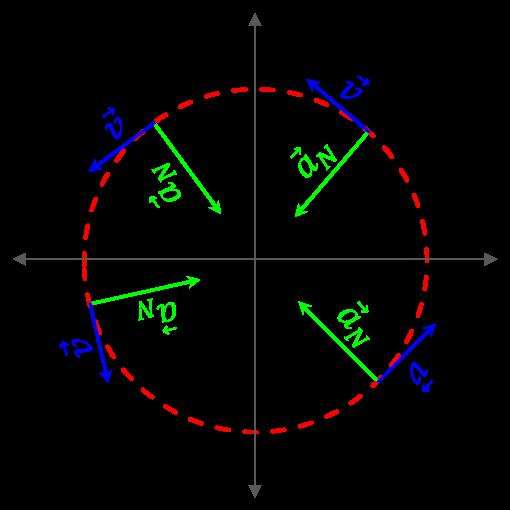
Нормальное ускорение направлено к центру кривизны траектории, поэтому его называют центростремительным. Причиной его возникновения являются центральные силы в системе, которые изменяют траекторию. Например, это сила гравитации при вращении планет вокруг звезд или сила натяжения веревки при вращении камня, привязанного к ней.

Полное ускорение при вращении по окружности

Разобравшись с понятиями и формулами тангенциального ускорения и нормального ускорения, можно теперь переходить к вычислению полного ускорения. Решим эту задачу на примере вращения тела по окружности вокруг некоторой оси.

Рассмотренные две компоненты ускорения направлены под углом 90o друг к другу (по касательной и к центру кривизны). Этот факт, а также свойство суммы векторов можно использовать, чтобы рассчитать ускорение полное. Получаем:

Из формулы полного, нормального и тангенциального ускорений (ускорения an и at) следует два важных вывода:

Во время движения по окружности центростремительная сила, сообщающая телу ускорение an, удерживает его на круговой орбите, препятствуя тем самым фиктивной центробежной силе.

Источник

Общее определение

Вам будет интересно: Чваниться — это некультурная привычка: толкование слова

То есть для вычисления величины a¯ необходимо найти производную вектора скорости по времени в данный момент. Формула показывает, что a¯ измеряется в метрах в секунду в квадрате (м/с2).

Направление полного ускорения a¯ никак не связано с вектором v¯. Однако оно совпадает с вектором dv¯.

Причиной появления у движущихся тел ускорения является действующая на них внешняя сила любой природы. Ускорение никогда не возникает, если внешняя сила равна нулю. Направление действия силы совпадает с направлением ускорения a¯.

Криволинейная траектория

В общем случае рассмотренная величина a¯ имеет две составляющие: нормальную и касательную. Но прежде всего напомним, что такое траектория. В физике под траекторией понимают линию, вдоль которой тело проходит некоторый путь в процессе движения. Поскольку траектория может представлять собой либо прямую линию, либо кривую, то движение тел делится на два типа:

В первом случае вектор скорости тела может измениться только на противоположный. Во втором же случае вектор скорости и ее абсолютное значение изменяются постоянно.

Как известно, скорость направлена по касательной к траектории. Этот факт позволяет ввести следующую формулу:

a¯ = dv¯/dt = d(v * u¯)/dt = dv/dt * u¯ + v * du¯/dt.

Нормальное ускорение точки

Обозначим эту компоненту ускорения символом an¯. Запишем для нее выражение еще раз:

Уравнение нормального ускорения an¯ можно записать в явном виде, если провести следующие математические преобразования:

an¯ = v * du¯/dt = v * du¯/d l* dl/dt = v2/r * re¯.

Центростремительная и центробежная силы

Во всех названных примерах сила центростремительная приводит к изменению прямолинейной траектории. В свою очередь, ей препятствуют инерционные свойства тела. С ними связывают центробежную силу. Эта сила, действуя на тело, пытается «выбросить» его из криволинейной траектории. Например, когда авто делает поворот, то пассажиров прижимает к одной из дверей транспортного средства. Это и есть действие центробежной силы. Она, в отличие от центростремительной, является фиктивной.

Пример задачи

Как известно, наша Земля вращается по круговой орбите вокруг Солнца. Необходимо определить нормальное ускорение голубой планеты.

Для решения задачи воспользуемся формулой:

Из справочных данных находим, что линейная скорость v нашей планеты составляет 29,78 км/с. Расстояние r до нашей звезды равно 149 597 871 км. Переводя эти числа в метры в секунду и метры, соответственно, подставляя их в формулу, получаем ответ: an = 0,006 м/с2, что составляет 0,06 % от величины ускорения свободного падения на планете.

Источник

НОРМАЛЬНОЕ УСКОРЕНИЕ

Полезное

Смотреть что такое «НОРМАЛЬНОЕ УСКОРЕНИЕ» в других словарях:

НОРМАЛЬНОЕ УСКОРЕНИЕ — составляющая ускорения точки при криволинейном движении, направленная по нормали к ее траектории в сторону центра кривизны. Нормальным ускорением называется также центростремительным. Нормальное ускорение численно равно v2/p, где v скорость точки … Большой Энциклопедический словарь

нормальное ускорение — центростремительное ускорение — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом Синонимы центростремительное ускорение EN normal acceleration … Справочник технического переводчика

нормальное ускорение — составляющая ускорения точки при криволинейном движении, направленная по нормали к её траектории в сторону центра кривизны. Нормальное ускорение называется также центростремительным. Нормальное ускорение численно равно υ2/ρ, где υ скорость точки … Энциклопедический словарь

нормальное ускорение — statmenasis pagreitis statusas T sritis Standartizacija ir metrologija apibrėžtis Pagreičio sandas, nukreiptas taško judėjimo trajektorijos svarbiausio statmens kryptimi. atitikmenys: angl. normal acceleration vok. Normalbeschleunigung, f rus.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

нормальное ускорение — normalinis pagreitis statusas T sritis fizika atitikmenys: angl. normal acceleration vok. Normalbeschleunigung, f rus. нормальное ускорение, n pranc. accélération normale, f … Fizikos terminų žodynas

Нормальное ускорение — составляющая ускорения (См. Ускорение) точки при криволинейном движении, направленная по главной нормали к траектории в сторону центра кривизны; Н. у. называется также центростремительным ускорением. Численно Н. у. равно v2/ρ, где v… … Большая советская энциклопедия

НОРМАЛЬНОЕ УСКОРЕНИЕ — центростремительное ускорение, составляющая ускорения точки при криволинейном движении, направленная по главной нормали к траектории точки в сторону центра кривизны. Н. у. ап = v2lr. где v скорость точки, r радиус кривизны траектории. При… … Большой энциклопедический политехнический словарь

НОРМАЛЬНОЕ УСКОРЕНИЕ — составляющая ускорения точки при криволинейном движении, направленная по нормали к её траектории в сторону центра кривизны. Н. у. наз. также центростремительным. Н. у. численно равно v2/p, где v скорость точки, р радиус кривизны траектории … Естествознание. Энциклопедический словарь

нормальное ускорение точки — Составляющая ускорения точки вдоль главной нормали к траектории при разложении ускорения по естественным осям. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984… … Справочник технического переводчика

нормальное ускорение точки — Составляющая ускорения точки вдоль главной нормали к траектории при разложении ускорения по естественным осям … Политехнический терминологический толковый словарь

Источник