Что показывает тангенс угла
Тангенс
Тангенс – одна из тригонометрических функций. Как и для всех других функций, значение тангенса определяется для конкретного угла или числа (в этом случае используют числовую окружность.
Аргумент и значение тангенса
Аргументом тангенса может быть:
— как число или выражение с Пи: \(1,3\), \(\frac<π><4>\), \(π\), \(-\frac<π><3>\) и т.п.
— так и угол в градусах: \(45^°\), \(360^°\),\(-800^°\), \(1^° \) и т.п.
Тангенс острого угла
1) Пусть дан угол и нужно определить тагенс этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить тангенс.
Вычисление тангенса числа или любого угла
Для чисел, а также для тупых, развернутых углов и углов больших \(360°\) тангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:
Пример. Вычислите \(tg\:0\).
Решение: Чтобы найти тангенс нуля нужно найти сначала синус и косинус \(0\). И то, и другое найдем с помощью тригонометрического круга :
Точка \(0\) на числовой окружности совпадает с \(1\) на оси косинусов, значит \(cos\:0=1\). Если из точки \(0\) на числовой окружности провести перпендикуляр к оси синусов, то мы попадем в точку \(0\), значит \(sin\:0=0\). Получается: \(tg\:0=\) \(\frac
Прямая проходящая через начало отсчета на числовой окружности и параллельная оси ординат (синусов) называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.
Ось тангенсов – это фактически копия оси синусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси синусов.
Чтобы определить тангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу тангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов.
3) Найти координату пересечения этой прямой и оси тангенсов.
2) Проводим через данную точку и начало координат прямую.
3) В данном случае координату долго искать не придется – она равняется \(1\).
Пример. Вычислите \(tg\: 45°\) и \(tg\: (-240°)\).
Решение:
Для угла \(45°\) (\(∠KOA\)) тангенс будет равен \(1\), потому что именно в таком значении сторона угла, проходящая через начало координат и точку \(A\), пересекает ось тангесов. А для угла \(-240°\) (\(∠KOB\)) тангенс равен \(-\sqrt<3>\) (приблизительно \(-1,73\)).
В отличие от синуса и косинуса значение тангенса не ограничено и лежит в пределах от \(-∞\) до \(+∞\), то есть может быть любым.
Так происходит потому, что прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось тангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках тангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений тангенс может быть найден).
Знаки по четвертям
Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение тангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение тангенса будет положительно (знак плюс).
С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.
Связь с другими тригонометрическими функциями:
Тригонометрия. Понятие тригонометрической величины (тангенс и котангенс).
Значение каждой тригонометрической величины изменяется с изменением угла, которому она соответствует, т.е. тригонометрическая величина это функция угла.
Линией тангенса (ADl, AD2 и т.д.) является отрезок касательной, проведенной через конец А первого диаметра, от точки касания до пересечения с продолжением подвижного радиуса (OMl, ОМ2 и. т.д.).
Линией котангенса (BEl, ВЕ2 и т.д.) является отрезок касательной, проведенной через конец В второго диаметра, от точки касания В до пересечения с продолжением подвижного радиуса (OM1, OM2 и т.д.).
Тангенс угла (tgх) – это отношение линии тангенса, взятого с соответствующим знаком, к радиусу.
Котангенс угла (сtgх) — отношение линии котангенса, взятого с соответствующим знаком, к радиусу.
Знаки тангенса и котангенса для различных четвертей указаны на рисунке ниже:
Секанс (secx) и косеканс (cosecx) проще всего определить как обратные величины косинуса и синуса.
Существуют законы, которые связывают все тригонометрические функции между собой, т. е позволяют их выражать одну через любую другую.
Тангенс
Тангенс (tg) — это отношение синуса к косинусу (tgα = sinα / cosα). Либо отношение противолежащего катета (дальнего/противоположного) к прилежащему (который находится рядом с углом).
В этом треугольнике тангенс угла вычисляется по этой формуле:
Обратите внимание, что в вычислении принимают участие только катеты, гипотенузы здесь нет (противолежащий делится на прилежащий — это тангенс острого угла прямоугольного треугольника).
Вычислите длину стороны BC, зная, что tan α = 0,4:
tan α = противолежащий катет / прилежащий катет = BC / AB = x / 15
x / 15 = 0,4 x = 15 * 0,4 x = 6
Таблица тангенсов и котангенсов (главных углов от 0° до 360°)
| α градусов | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| α радиан | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| tg α | 0 | √3/3 | 1 | √3 | – | 0 | – | 0 |
| ctg α | – | √3 | 1 | √3/3 | 0 | – | 0 | – |
Основные тригонометрические тождества
Что такое синус?
Синус угла (sin) — это отношение противолежащего катета (который находится напротив угла) к гипотенузе (самой длинной стороне, находится напротив прямого угла).
В нашем примере sin α = BC/AC.
Что такое косинус?
Косинус угла (cos) — это отношение прилежащего катета (находится рядом с углом) к гипотенузе (самой длинной стороне, находится напротив прямого угла). В нашем примере cos α = AB/AC.
Что такое котангенс?
Котангенс угла (ctg) — это отношение прилежащего катета (который находится рядом с углом) к противолежащему (напротив угла). В нашем примере ctg α = AB / BC. Обратите внимание, что котангенс — это как «тангенс наоборот» (прилежащий делится на противолежащий), т. е. ctg α = AB / BC, а tg α = BC / AB (противолежащий делится на прилежащий).
Что такое секанс?
Секанс (sec или sec x) — это отношение гипотенузы (самой длинной стороны, напротив прямого угла) к прилежащему катету (рядом с углом) острого угла в прямоугольном треугольнике. Ещё секанс определяется формулой:
Что такое гипотенуза и катет?
Гипотенуза — это та сторона, которая находится напротив прямого угла (она самая длинная), в нашем треугольнике это сторона AC. Катеты — это две другие стороны, которые находятся рядом с прямым углом, в нашем треугольнике это стороны BC и AB:
Тангенс — что это такое (отношение чего к чему) и как его найти (по формулам и по клеточкам)
Как пользоваться таблицей Брадиса.
На некоторых примерах рассмотрим, как пользоваться таблицей Брадиса.
sin 7° = 0.1219 (косинусы находятся внизу) cos 82° = 0.1392.
sin 3°42′ = 0.0645 (ниже на изображении отмечено красным) cos 80°24′ = 0.1668.
Обратите внимание, все тоже самое верно и при определении значений тангенса и котангенса.
Далее рассмотрим вариант посложнее, когда угол, который представлен в таблице не указан, значит, нужно выбирать более близкое к нему значение (из значений, которые указаны в таблице синусов и косинусов), а на разницу, которая может составлять 1′,2′,3′, берем поправку из минут (желтая графа), как видно на примере:
sin 3°45′=sin 3°42′+3′=0.0645+0.0009=0.0654 либо
sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654
Кроме того, нужно помнить правило: для синуса у поправки неотрицательный знак, а у косинуса неположительный.
cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 либо
Решение уравнения tg x = a
| Обычная форма записи решения: |  |
| Более удобная форма записи решения |  |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Графическое обоснование решения уравнения tg x = a представлено на рисунке 3.
Частные случаи решения уравнений tg x = a
| Уравнение | Решение |
 |  |
| tg x = – 1 |  |
 |  |
| tg x = 0 |  |
 |  |
| tg x = 1 |  |
 |  |
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тригонометрические функции и их значение в изучении геометрии
В геометрии особую роль имеют тригонометрические функции, при помощи которых определяют, как относятся между собой стороны и углы прямоугольного треугольника. Конечно, тригонометрия не стоит на месте и со времен Евклида она намного шагнула вперёд и теперь может эти функции могут выражаться через решение дифференциальных уравнений.
В данный момент используются шесть обозначений для основных тригонометрических функций, причем четыре функции из шести, они стоят в ряду последними, можно определять не только с помощью геометрии.
Синус (sin)
Косинус (cos)
Тангенс (tg/tan)
Котангенс (ctg/cot)
Секанс (sec)
Косеканс (cosec/csc) 
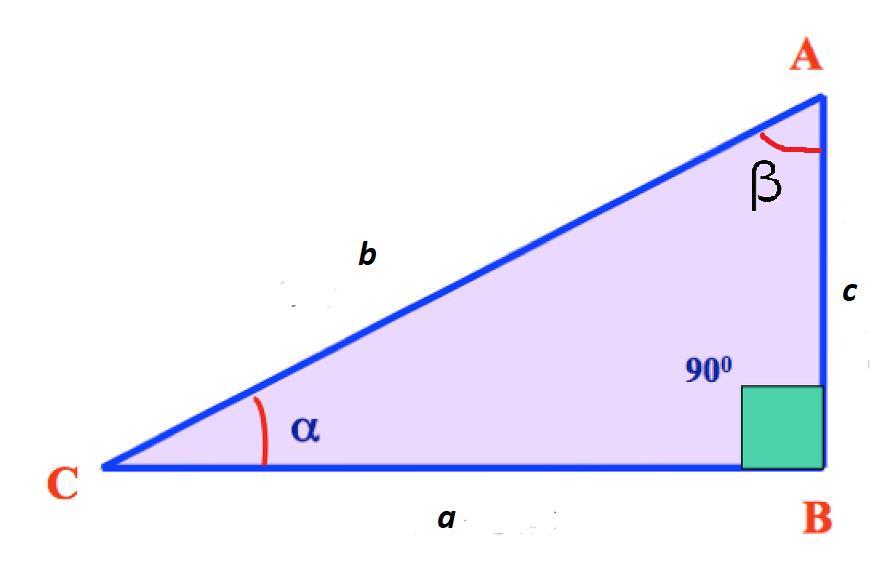
Рассмотрим сам прямоугольный треугольник, обозначения его сторон и углов во всех справочниках, как обычно, стандартные, какой бы стороной он не лежал бы на плоскости.
В этом треугольнике различают три угла, обозначаемые α, β, γ, при этом γ всегда 90°. Сторона, лежащая напротив прямого угла γ, называется гипотенузой, она обозначается буквой С. Угол α, с него начинаются все расчеты, находится напротив стороны а / ВС/, называемой противолежащей к этому углу, и сторона b /АС/, которая находится рядом, подлежит к этому углу и называется прилежащей.
По Евклидовой теории, которая верна до сих пор (и будет верна всегда), суммы углов такого треугольника, который находится в одной плоскости, будет равна 180 или числу π. И значение любого угла будут находиться в пределах между 0 и π /2.
Тогда тригонометрические функции можно выразить через размеры сторон этого треугольника. Так как угол α является первым и в греческом алфавите и в нашем треугольнике, начинаем знакомство с функциями через этот угол.
Эти функции можно выразить и через окружность путем задания системы координат. Задаем систему координат с центом в точке О. Угол, на который поворачивается отрезок ОА, изображенный на чертеже, будем считать произвольным, назовем его θ.
Тогда тангенсом этого угла θсчитается отношение ординаты точки А на окружности к её абсциссе. Следовательно, если ctg α = b : а, а АС = sin θ, ОС = cos θ, то tgθ = sin θ : cos θ. Аналогично получаем ctg θ = cos θ : sin θ или 1 : tgθ.
Тангенс — это отношение…
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Применение функции тангенса для решения задач
Что бы научиться пользоваться этой функцией, Нужно попробовать решить несколько примеров по применению этой функции.
Пример: есть два катета ВС = 7 см и АС = 12 см. Нам нужно узнать все остальные данные о треугольнике.
Первая формула, это tg α = а : b. тогда tg α = 7 :12= 0, 5833, далее для нахождения угла α используем таблицы Брадиса. На пересечении градусов и минут находим ближайшее значение угла – 0,5844, соответствующее 30° и 18′.
Находим ближайшую поправку, разную 3′. Отнимаем ее от нашего угла и получаем угол α = 30° 15′. Второй угол находим, исходя из того, что сумма всех углов должна быть не больше 180°, а угол γ = 90° по условию. Тогда угол β = 90° – 30° 15′= 59°45′.
Нам осталось найти гипотенузу с.
Можем найти её через sin α, который равен а: с, тогда с = а : sin α.
Находим sin α через таблицу Брадиса. Ближайшее значение 30° 36′, будет 0,5060, тогда не хватает 3′, Что по полям поправок равно 0,0008. Добавляем это число к найденному: 0, 5060 + 0,0008 = 0,5068. Подставляем это значение в формулу, с = 7:0,5068, с = 13, 8 см. Задача решена.
Можно искать значение углов через значение числа π, которое равно 180°. Тогда наиболее популярные углы, такие, как тангенс 30 градусов, тангенс 0 градусов, тангенс 60 градусов, тангенс 90 градусов, тангенс 45 градусов, тангенс 15 градусов, тангенс 75 градусов можно рассматривать намного проще. Нужно знать, что тангенс 0 градусов равен 0, а тангенс 90 градусов не имеет конкретного значения.
Можно найти тангенс угла 5 градусов, который равен 0, 0875 и добавлять или отнимать от наиболее часто встречающихся углов. Например угол 45 градусов, его тангенс равен 1, тогда тангенс угла 50 градусов будет равен 1, 0875. Тангенс 35 градусов можно рассчитать путем добавления к тангенсу 30 градусов угол 5 градусов, а тангенс 10 градусов это удвоение угла 5 градусов.
Для удобства есть рассчитанная таблица основных углов через значение π.
| Значение угла α (градусов) | Значение угла α в радианах | tg (тангенс) |
|---|---|---|
| Тангенс 0 | 0 | 0 |
| Тангенс 15 | π/12 | 0.2679 |
| Тангенс 30 | π/6 | 0.5774 |
| Тангенс 45 | π/4 | 1 |
| Тангенс 50 | 5π/18 | 5114 |
| Тангенс 60 | π/3 | 1.7321 |
| Тангенс 65 | 13π/36 | 2.1445 |
| Тангенс 70 | 7π/18 | 2.7475 |
| Тангенс 75 | 5π/12 | 3.7321 |
| Тангенс 90 | π/2 | – |
| Тангенс 105 | 5π/12 | -3.7321 |
| Тангенс 120 | 2π/3 | -1.7321 |
| Тангенс 135 | 3π/4 | -1 |
| Тангенс 140 | 7π/9 | -0.8391 |
| Тангенс 150 | 5π/6 | -0.5774 |
| Тангенс 180 | π | 0 |
| Тангенс 270 | 3π/2 | – |
| Тангенс 360 | 2π | 0 |
Если угол больше 90 градусов, нужно помнить, что функции имеют свойство повторяться, поэтому, если ищем тангенс 145 градусов, тогда 180 – 145 = 35 градусов, но уже со знаком «минус», это можно понять по чертежу окружности, где положительное или отрицательное значение абсциссы и ординаты. Научиться быстро пользоваться таблицами Брадиса и рассчитывать значения треугольника совсем не сложно, главное, уловить суть процесса.
Тангенс угла это отношение чего? Основы тригонометрии
Определение

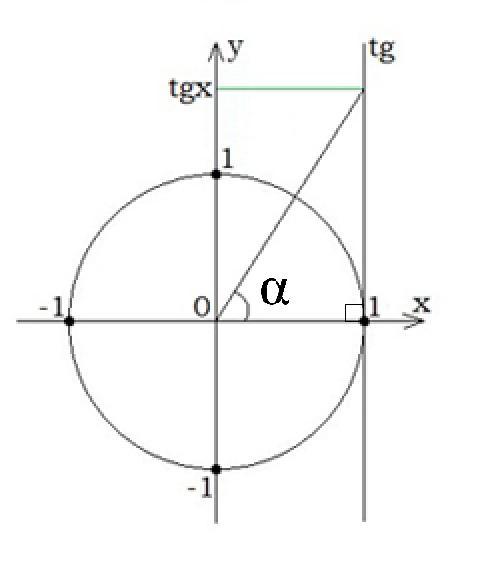
Теперь перейдем к определению тангенса, которое несет алгебраический смысл, для этого нам понадобится единичная окружность.
Для того чтобы отметить в декартовой системе координат численное значение тангенса необходимо для начала провести прямую х = 1, которая будет перпендикулярна оси абсцисс и параллельна оси ординат. После чего отложим от оси абсцисс угол альфа и продлим его сторону до пересечения с прямой х = 1. Ордината точки пересечения в конкретной ситуации будет являться численным значением тангенса отложенного угла.
Как связаны тангенс с котангенсом?
Тангенс является обратной функцией от котангенса, а это значит что: tg = 1/ctg. Таким образом, отношение тангенса к котангенсу является равным единице: tg/ctg = 1.
Существует ли связь тангенса с косинусом?
Существует такое тождество, определяющее связь этих двух тригонометрических функций: 1 + tg2 = 1/cos2. Попробуем доказать это тождество, преобразуя его левую часть с помощью алгебраического определения тангенса:
Теперь приведем выражение к общему знаменателю:
Вспомним главное тригонометрическое тождество и упростим выражение, после чего получим:
Эта дробь является равной правой части данного изначально выражения, таким образом мы доказали тождество.