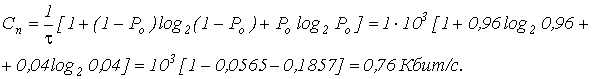Что понимается под каналом связи
Понятие, характеристики и состав канала связи.



Канал связи предназначен для передачи сигналов между удаленными устройствами. Сигналы несут информацию, предназначенную для представления пользователю (человеку), либо для использования прикладными программами ЭВМ.
2 Канал связи включает следующие компоненты:
1) передающее устройство;
2) приемное устройство;
3) среду передачи различной физической природы
Формируемый передатчиком сигнал, несущий информацию, после прохождения через среду передачи поступает на вход приемного устройства. Далее информация выделяется из сигнала и передается потребителю. Физическая природа сигнала выбирается таким образом, чтобы он мог распространяться через среду передачи с минимальным ослаблением и искажениями. Сигнал необходим в качестве переносчика информации, сам он информации не несет. канал связь удаленный получатель
3. Характеристики (параметры) каналов связи
1. Передаточная функция канала: представляется в виде амплитудно-частотной характеристики (АЧХ) и показывает, как затухает амплитуда синусоиды на выходе канала связи по сравнению с амплитудой на ее входе для всех возможных частот передаваемого сигнала. Знание амплитудно-частотной характеристики реального канала позволяет определить форму выходного сигнала практически для любого входного сигнала. Для этого необходимо найти спектр входного сигнала, преобразовать амплитуду составляющих его гармоник в соответствии с амплитудно-частотной характеристикой, а затем найти форму выходного сигнала, сложив преобразованные гармоники. Для экспериментальной проверки амплитудно-частотной характеристики нужно провести тестирование канала эталонными (равными по амплитуде) синусоидами по всему диапазону частот от нуля до некоторого максимального значения, которое может встретиться во входных сигналах. Причем менять частоту входных синусоид нужно с небольшим шагом, а значит количество экспериментов должно быть большим.
2. Полоса пропускания: является производной характеристикой от АЧХ. Она представляет собой непрерывный диапазон частот, для которых отношение амплитуды выходного сигнала к входному превышает некоторый заранее заданный предел, то есть полоса пропускания определяет диапазон частот сигнала, при которых этот сигнал передается по каналу связи без значительных искажений. Обычно полоса пропускания отсчитывается на уровне 0,7 от максимального значения АЧХ. Ширина полосы пропускания в наибольшей степени влияет на максимально возможную скорость передачи информации по каналу связи.
3. Затухание: определяется как относительное уменьшение амплитуды или мощности сигнала при передаче по каналу сигнала определенной частоты. Часто при эксплуатации канала заранее известна основная частота передаваемого сигнала, то есть та частота, гармоника которой имеет наибольшую амплитуду и мощность. Поэтому достаточно знать
затухание на этой частоте, чтобы приблизительно оценить искажения передаваемых по каналу сигналов. Более точные оценки возможны при знании затухания на нескольких частотах, соответствующих нескольким основным гармоникам передаваемого сигнала.
Затухание обычно измеряется в децибелах (дБ) и вычисляется по следующей формуле:
Затухание всегда рассчитывается для определенной частоты и соотносится с длиной канала. На практике всегда пользуются понятием «погонное затухание», т.е. затухание сигнала на единицу длины канала, например, затухание 0.1 дБ/метр.
5. Помехоустойчивость канала: характеризует его способность обеспечивать передачу сигналов в условиях помех. Помехи принято делить на внутренние (представляет собой тепловые шумы аппаратуры) и внешние (они многообразны и зависят от среды передачи). Помехоустойчивость канала зависит от аппаратных и алгоритмических решений по обработке принятого сигнала, которые заложены в приемо-передающее устройство. Помехоустойчивость передачи сигналов через канал может быть повышена за счет кодирования и специальной обработки сигнала.
6. Динамический диапазон: логарифм отношения максимальной мощности сигналов, пропускаемых каналом, к минимальной.
7. Помехозащищенность: это помехозащищенность, т.е. помехозащищенность.
Классификация и характеристики канала связи



Канал связи – это совокупность средств, предназначенных для передачи сигналов (сообщений).
Для анализа информационных процессов в канале связи можно использовать его обобщенную схему, приведенную на рис. 1.
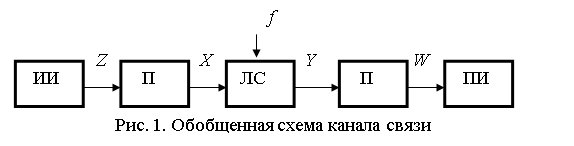 |
На рис. 1 приняты следующие обозначения: X, Y, Z, W – сигналы, сообщения; f – помеха; ЛС – линия связи; ИИ, ПИ – источник и приемник информации; П – преобразователи (кодирование, модуляция, декодирование, демодуляция).
Существуют различные типы каналов, которые можно классифицировать по различным признакам:
1. По типу линий связи: проводные; кабельные; оптико-волоконные;
линии электропередачи; радиоканалы и т.д.
2. По характеру сигналов: непрерывные; дискретные; дискретно-непрерывные (сигналы на входе системы дискретные, а на выходе непрерывные, и наоборот).
3. По помехозащищенности: каналы без помех; с помехами.
Каналы связи характеризуются:
1. Емкость канала определяется как произведениевремени использования канала Tк, ширины спектра частот, пропускаемых каналом Fк и динамического диапазона Dк., который характеризует способность канала передавать различные уровни сигналов
2.Скорость передачи информации – среднее количество информации, передаваемое в единицу времени.
3. Пропускная способность канала связи – наибольшая теоретически достижимая скорость передачи информации при условии, что погрешность не превосходит заданной величины.
4. Избыточность – обеспечивает достоверность передаваемой информации (R = 0¸1).
Одной из задач теории информации является определение зависимости скорости передачи информации и пропускной способности канала связи от параметров канала и характеристик сигналов и помех.
Канал связи образно можно сравнивать с дорогами. Узкие дороги – малая пропускная способность, но дешево. Широкие дороги – хорошая пропускная способность, но дорого. Пропускная способность определяется самым «узким» местом.
Скорость передачи данных в значительной мере зависит от передающей среды в каналах связи, в качестве которых используются различные типы линий связи.
Проводные:
1. Проводные– витая пара (что частично подавляет электромагнитное излучение других источников). Скорость передачи до 1 Мбит/с. Используется в телефонных сетях и для передачи данных.
2. Коаксиальный кабель.Скорость передачи 10–100 Мбит/с – используется в локальных сетях, кабельном телевидении и т.д.
3. Оптико-волоконная.Скорость передачи 1 Гбит/с.
В средах 1–3 затухание в дБ линейно зависит от расстояния, т.е. мощность падает по экспоненте. Поэтому через определенное расстояние необходимо ставить регенераторы (усилители).
Радиолинии:
1. Радиоканал.Скорость передачи 100–400 Кбит/с. Использует радиочастоты до 1000 МГц. До 30 МГц за счет отражения от ионосферы возможно распространение электромагнитных волн за пределы прямой видимости. Но этот диапазон сильно зашумлен (например, любительской радиосвязью). От 30 до 1000 МГц – ионосфера прозрачна и необходима прямая видимость. Антенны устанавливаются на высоте (иногда устанавливаются регенераторы). Используются в радио и телевидении.
2. Микроволновые линии.Скорости передачи до 1 Гбит/с. Используют радиочастоты выше 1000 МГц. При этом необходима прямая видимость и остронаправленные параболические антенны. Расстояние между регенераторами 10–200 км. Используются для телефонной связи, телевидения и передачи данных.
3. Спутниковая связь. Используются микроволновые частоты, а спутник служит регенератором (причем для многих станций). Характеристики те же, что у микроволновых линий.
2 Пропускная способность дискретного канала связи
Дискретный канал представляет собой совокупность средств, предназначенных для передачи дискретных сигналов [5].
Пропускная способность канала связи – наибольшая теоретически достижимая скорость передачи информации при условии, что погрешность не превосходит заданной величины.Скорость передачи информации – среднее количество информации, передаваемое в единицу времени. Определим выражения для расчета скорости передачи информации и пропускной способности дискретного канала связи.
При передаче каждого символа в среднем по каналу связи проходит количество информации, определяемое по формуле
I (Y, X) = I (X, Y) = H(X) – H (X/Y) = H(Y) – H (Y/X), (2)
где: I (Y, X) – взаимная информация, т.е.количество информации, содержащееся в Y относительно X; H(X) – энтропия источника сообщений; H (X/Y) – условная энтропия, определяющая потерю информации на один символ, связанную с наличием помех и искажений.
При передаче сообщения XT длительности T, состоящего из n элементарных символов, среднее количество передаваемой информации с учетом симметрии взаимного количества информации равно:
I(YT, XT) = H(XT) – H(XT/YT) = H(YT) – H(YT/XT) = n [H(X) – H (X/Y), (3)
где T = n 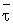
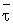
Для символов равной длительности 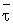
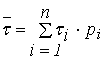
При этом скорость передачи информации
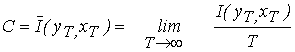
Скорость передачи информации зависит от статистических свойств источника, метода кодирования и свойств канала.
Пропускная способность дискретного канала связи
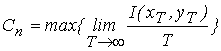
Максимально-возможное значение, т.е. максимум функционала ищется на всем множестве функций распределения вероятности p(x).
Пропускная способность зависит от технических характеристик канала (быстродействия аппаратуры, вида модуляции, уровня помех и искажений и т.д.). Единицами измерения пропускной способности канала являются: [bit/s], [Kbit/s], [Mbit/s], [Gbit/s].
2.1 Дискретный канал связи без помех
Если помехи в канале связи отсутствуют, то входные и выходные сигналы канала связаны однозначной, функциональной зависимостью.
При этом условная энтропия равна нулю, а безусловные энтропии источника и приемника равны, т.е. среднее количество информации в принятом символе относительно переданного равно
I (X, Y) = H(X) = H(Y); H (X/Y) = 0.
Если ХТ – количество символов за время T, то скорость передачи информации для дискретного канала связи без помех равна
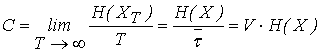
где V = 1/ 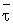
Пропускная способность для дискретного канала связи без помех
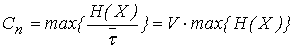
Т.к. максимальная энтропия соответствует для равновероятных символов, то пропускная способность для равномерного распределения и статистической независимости передаваемых символов равна:
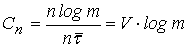
Первая теорема Шеннона для канала:Если поток информации, вырабатываемый источником, достаточно близок к пропускной способности канала связи, т.е.
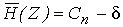
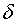
то всегда можно найти такой способ кодирования, который обеспечит передачу всех сообщений источника, причем скорость передачи информации будет весьма близкой к пропускной способности канала.
Теорема не отвечает на вопрос, каким образом осуществлять кодирование.
Пример 1. Источник вырабатывает 3 сообщения с вероятностями:
p1 = 0,1; p2 = 0,2 и p3 = 0,7.
Сообщения независимы и передаются равномерным двоичным кодом (m = 2) с длительностью символов, равной 1 мс. Определить скорость передачи информации по каналу связи без помех.
Решение: Энтропия источника равна
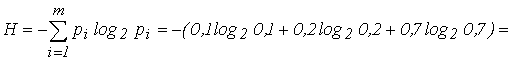
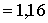
Для передачи 3 сообщений равномерным кодом необходимо два разряда, при этом длительность кодовой комбинации равна 2t.
Средняя скорость передачи сигнала
V =1/2t = 500 [1/c].
Скорость передачи информации
C = vH = 500×1,16 = 580 [бит/с].
2.2 Дискретный канал связи с помехами
Мы будем рассматривать дискретные каналы связи без памяти.
Каналом без памяти называется канал, в котором на каждый передаваемый символ сигнала, помехи воздействуют, не зависимо от того, какие сигналы передавались ранее. То есть помехи не создают дополнительные коррелятивные связи между символами. Название «без памяти» означает, что при очередной передаче канал как бы не помнит результатов предыдущих передач.
При наличии помехи среднее количество информации в принятом символе сообщении – Y, относительно переданного – X равно:
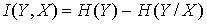
Для символа сообщения XT длительности T, состоящегоиз n элементарных символов среднее количество информации в принятом символе сообщении – YT относительно переданного – XT равно:
I(YT, XT) = H(XT) – H(XT/YT) = H(YT) – H(YT/XT) = n [H(Y) – H (Y/X). (9)
Для определения потерь в дискретном канале связи используется канальная матрица (матрица переходных вероятностей), позволяющая определить условную энтропию характеризующую потерю информации на символ сообщения.
Скорость передачи информации по дискретному каналу с помехами
равна:
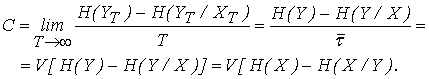
Пропускная способность дискретного канала при наличии помех равна максимально допустимой скорости передачи информации, причем максимум разыскивается по всем распределениям вероятностей p(x) на X и, поскольку, энтропия максимальна для равномерного распределения (для равновероятных символов сообщения), то выражение для пропускной способности имеет вид:
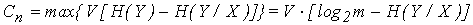
Как видно из формулы, наличие помех уменьшает пропускную способность канала связи.
Пример. По каналу связи передаются сообщения, вероятности которых соответственно равны:
p(x1)=0,1; p(x2)=0,2; p(x3)=0,3; p(x4)=0,4.
Канальная матрица, определяющая потери информации в канале связи имеет вид:




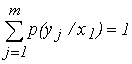
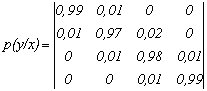
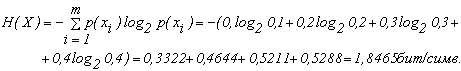
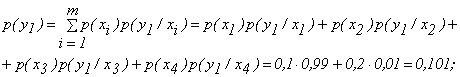
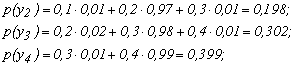
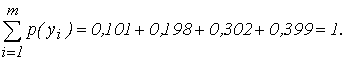
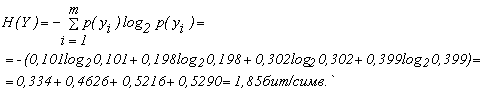

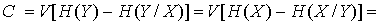

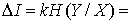 500×0,132=66 бит.
500×0,132=66 бит. 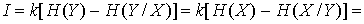
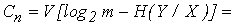 (2–0,132)/0,0001=18,68 Кбит/с.
(2–0,132)/0,0001=18,68 Кбит/с. 
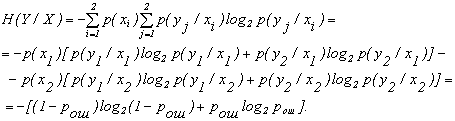
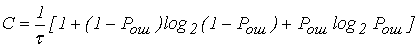 (12)
(12) 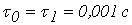 , если шумы в канале вносят ошибки, таким образом, что в среднем 4 символа из 100 принимаются неверно (т.е. «1» вместо «0» и наоборот).
, если шумы в канале вносят ошибки, таким образом, что в среднем 4 символа из 100 принимаются неверно (т.е. «1» вместо «0» и наоборот).