Что понимается под обратимостью чертежа
Обратимость чертежа
Инвариантные свойства ортогонального проецирования
К чертежу предъявляются следующие требования: точность, простота, наглядность и обратимость.
Чертеж называется обратимым, если по изображению фигуры можно восстановить ее форму, размеры и положение в пространстве.
|
|
|
|
Обратимость чертежа может быть обеспечена проецированием на две (три) непараллельные плоскости проекций.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Обратимость чертежа
Вышеприведенные чертежи называются однокартинными. Однокартинный чертеж не обладает свойством обратимости. Проекционный чертеж становится обратимым при добавлении дополнительной информации.
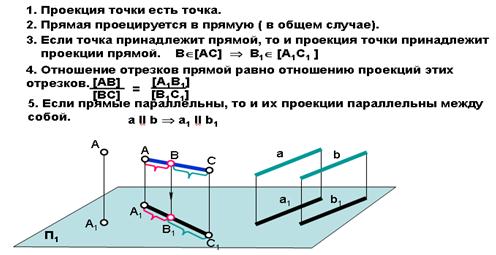
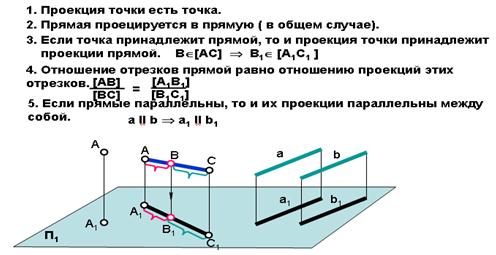
горизонтальная проекция точки А; А2 – фронтальная проекция точки А; А1А2— линия связи. Если на К.Ч. заданы две проекции точки, точка однозначно задана на К.Ч.
На рис. 7 приведен комплексный чертеж прямой АВ. Прямая однозначно задана на комплексном чертеже, если заданы две ее проекции.
Взаимное расположение двух прямых.
| Рис. 8 |
| Рис.10 |
| Рис.9 |
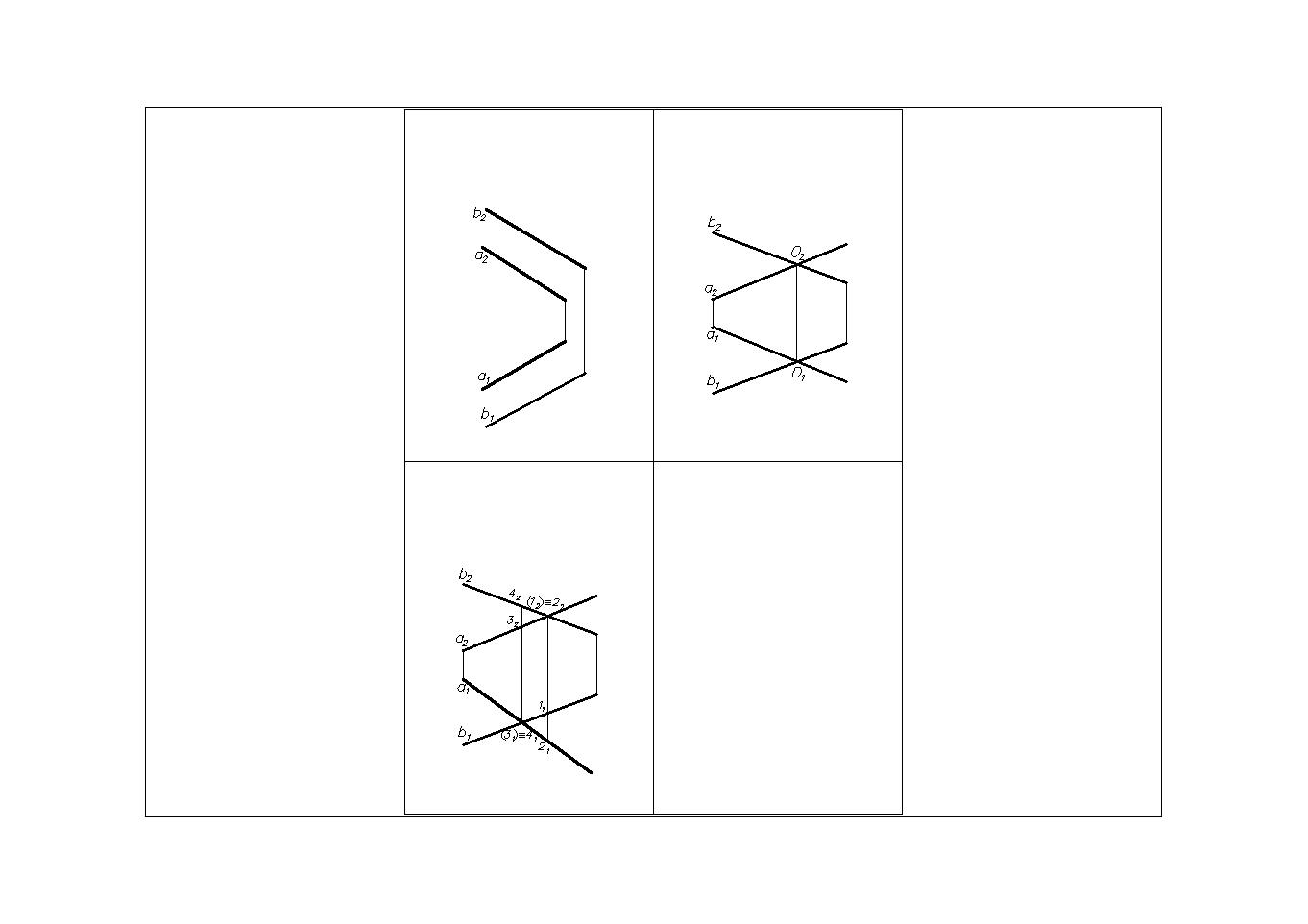
1. Параллельные прямые. Две прямые параллельны между собой, если их одноименные проекции тоже параллельны (Рис.8). Если aIIb, то a1IIb1и a2IIb2.
2. Пересекающиеся прямые (имеют одну общую точку). Две прямые пересекаются между собой, если точки пересечения одноименных проекций прямых лежат на одной линии связи (Рис.9). Если a xb = О,тоa1xb1 = О1 иa2xb2. = О2.
3. Скрещивающиеся прямые (не имеют общих точек). Две прямые скрещиваются между собой, если точки пересечения их одноименных проекций лежат на разных линиях связи (Рис.10).
Положение прямых линий относительно
плоскостей проекций.
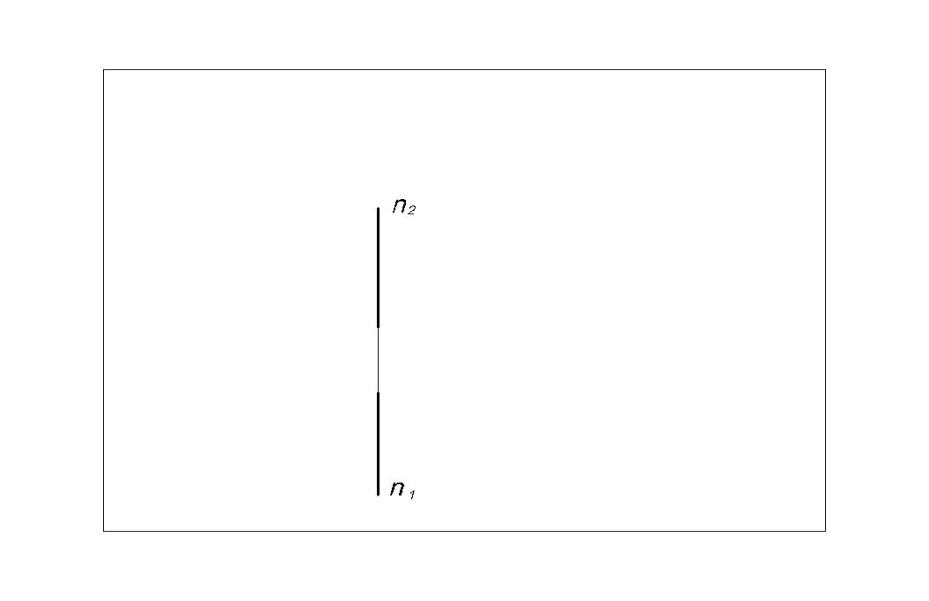
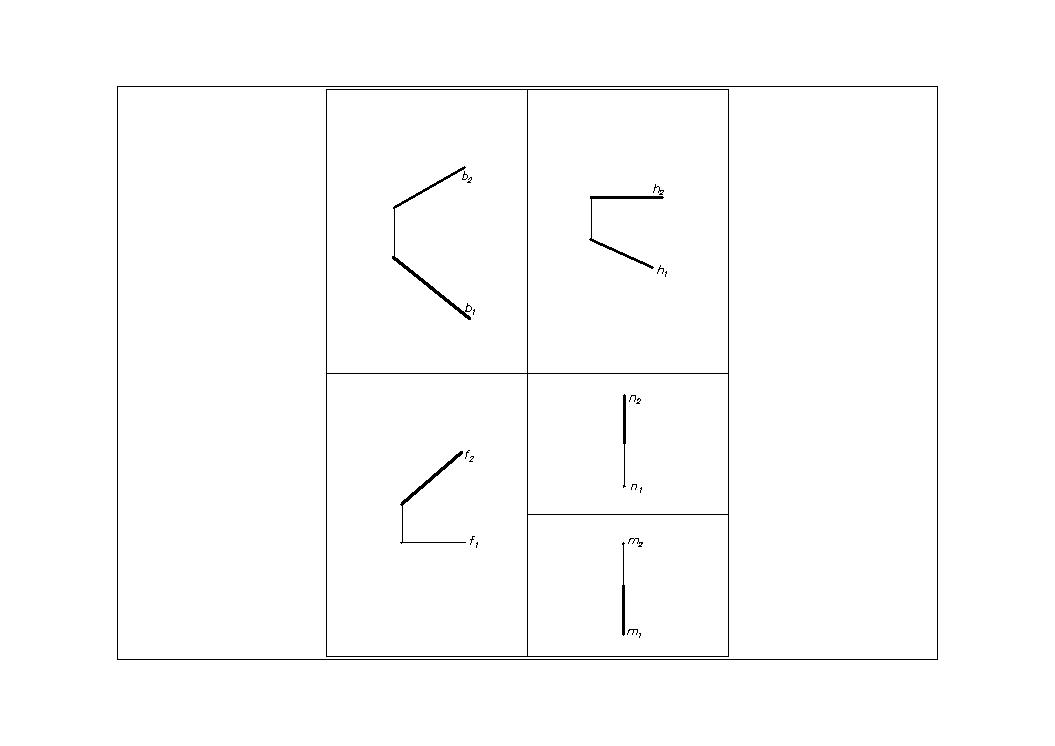
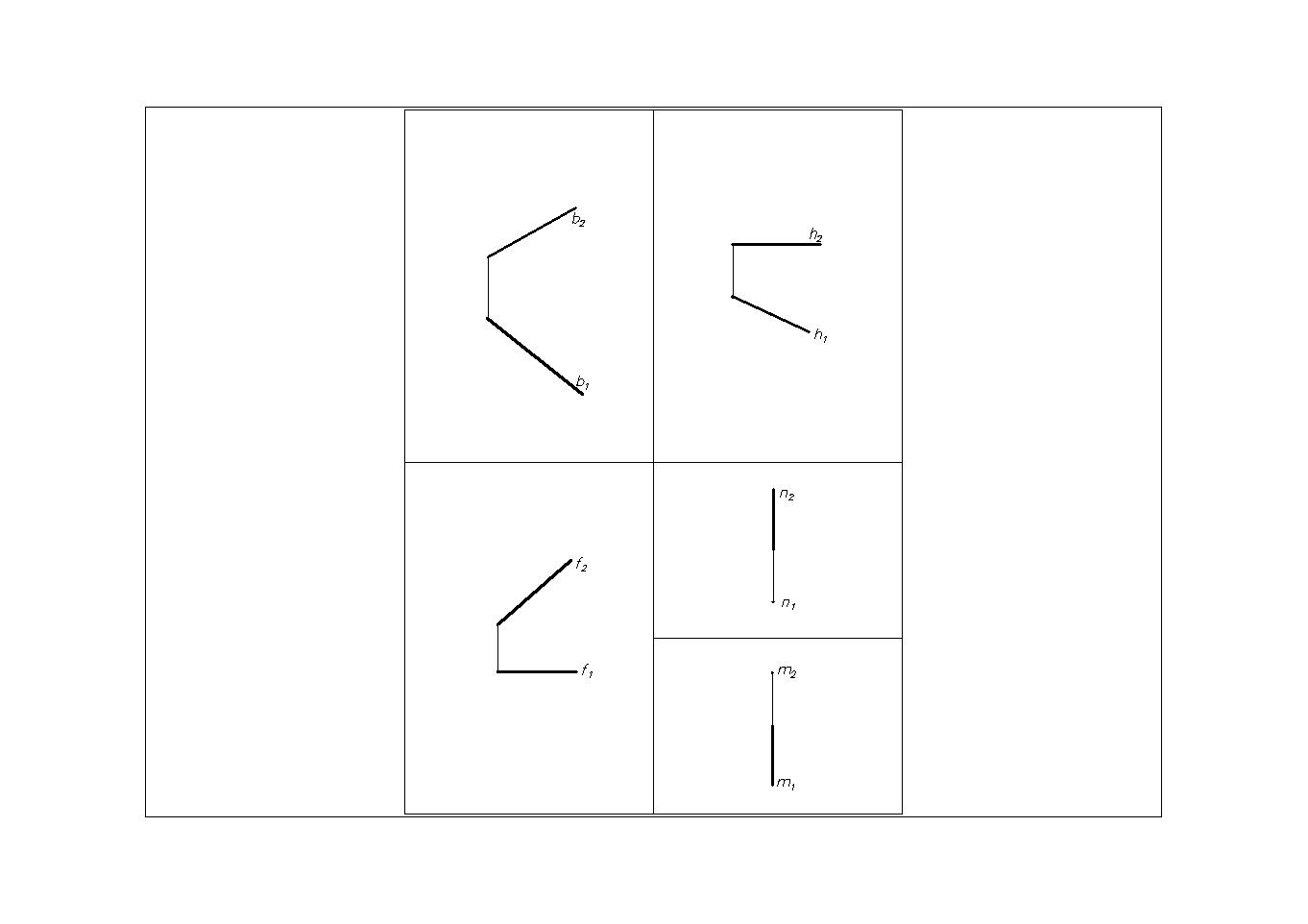
Рис.11 Рис.12 Рис.13 Рис.14
В зависимости от своего положения относительно плоскостей проекций прямые разделяют на прямые общего положения и прямые частного положения.
Прямая общего положения (Рис.11) – прямая, которая имеет углы, отличные от 0 и 90 одновременно со всеми плоскостями проекции (П1, П2).
Прямые, которые параллельны плоскостям проекций или перпендикулярные к ним называются прямыми частного положения.
Фронталь (Рис.13) – линия, все точки которой имеют одинаковую координату Y (ордината). Фронталь параллельна фронтальной плоскости проекций. Обозначение фронтали – f(fIIП2). На П2 f2= f, f2— натуральная величина отрезка АВ.
Профильная линия(Рис.14)– линия, все точки которой имеют одинаковую координату X (абсцисса). Профильная линияпараллельна профильной плоскости проекций. Обозначим профильную линию буквой п (пII П3). На П1 и П2 проекции профильной линии п совпадают с линией связи.
Обратимость чертежа
Инвариантные свойства ортогонального проецирования
К чертежу предъявляются следующие требования: точность, простота, наглядность и обратимость.
Чертеж называется обратимым, если по изображению фигуры можно восстановить ее форму, размеры и положение в пространстве.
|
|
|
|
Обратимость чертежа может быть обеспечена проецированием на две (три) непараллельные плоскости проекций.
Обратимость чертежа. Метод Монжа
Чтобы чертеж был равноценен изображаемому предмету, к нему предъявляют особые требования это обратимость, точность, наглядность.
Рассмотренные методы проецирования позволяют решать прямую задачу:
строить проекционный чертеж объекта. Однако обратная задача не решается однозначно по проекционному чертежу нельзя воспроизвести, восстановить оригинал.
По единственной проекции Аπ (рисунок 8) невозможно определить положение самой точки А в пространстве или хотя бы расстояние от точки до
плоскости проекций π. По проекции на плоскости Mπ Nπ отрезка MN
(рисунок 9) нельзя найти длину этого отрезка.
Таким образом, все рассмотренные выше чертежи, имеющие одну проекцию объекта, не обладают свойством обратимости. Для однозначности решения обратной задачи необходимо проецирование оригинала на несколько
плоскостей, что и было предложено выдающимся ученым геометром
КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ
1. Что называется проекцией, проецированием и каковы основные способы проецирования?
2. Сущность центрального и параллельного проецирования.
3. Что представляет собой метод ортогональных проекций (метод Монжа)?
4. Какие знаете свойства ортогонального проецирования?
5. В чем заключается обратимость чертежа?
6. Определяет ли одна проекция точки ее положение в пространстве?
1. Проецирование, при котором проецирующие лучи выходят из одной точки, называется:__.
а) ортогональным б) центральным
2. В начертательной геометрии используют
методы решения задач.
3. Угол наклона проецирующих лучей к плоскости проекций при ортогональном проецировании составляет:__.
г) произвольное число градусов
5. Любая пространственная форма рассматривается как множество
а) кривых б) точек в) прямых
6. Плоская фигура, параллельная плоскости проекции, проецируется в
натуральную величину при использовании
7. Предметом начертательной геометрии является
.
8. Однозначное соответствие между проецируемым объектом и его изображением называется чертежа.
Материал взят из книги Азбука начертательной геометрии (Маркова, О. А.)