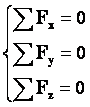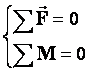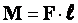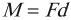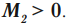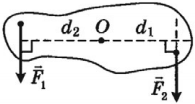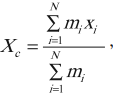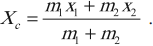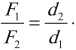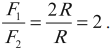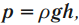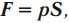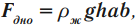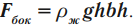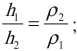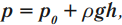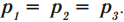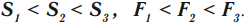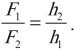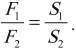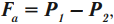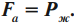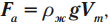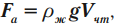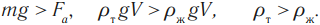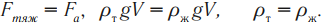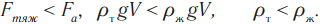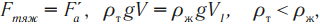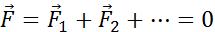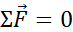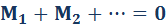Что понимается под равновесием в статике

Статика. Равновесие механической системы (абсолютно твердого тела).

Равновесие механической системы — это состояние, при котором все точки механической системы находятся в покое по отношению к рассматриваемой системе отсчета. Если система отсчета инерциальна, равновесие называется абсолютным, если неинерциальна — относительным.

Для нахождения условий равновесия абсолютно твердого тела необходимо мысленно разбить его на большое число достаточно малых элементов, каждый из которых можно представить материальной точкой. Все эти элементы взаимодействуют между собой — эти силы взаимодействия называются внутренними. Помимо этого на ряд точек тела могут действовать внешние силы.

Согласно второму закону Ньютона, чтобы ускорение точки равнялось нулю (а ускорение покоящейся точки равно нулю), геометрическая сумма сил, действующих на эту точку, должна быть равна нулю. Если тело находится в покое, значит, все его точки (элементы) также находятся в покое. Следовательно, для любой точки тела можно записать:

где — геометрическая сумма всех внешних и внутренних сил, действующих на i-й элемент тела.

Уравнение означает, что для равновесия тела необходимо и достаточно, чтобы геометрическая сумма всех сил, действующих на любой элемент этого тела, была равна нулю.

Из легко получить первое условие равновесия тела (системы тел). Для этого достаточно просуммировать уравнение по всем элементам тела:

.

Вторая сумма равна нулю согласно третьему закону Ньютона: векторная сумма всех внутренних сил системы равна нулю, т. к. любой внутренней силе соответствует сила, равная по модулю и противоположная по направлению.

.

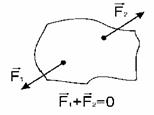
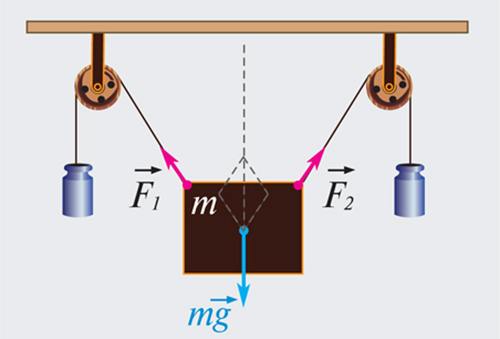
Первым условием равновесия твердого тела (системы тел) является равенство нулю геометрической суммы всех внешних сил, приложенных к телу.

Это условие является необходимым, но не достаточным. В этом легко убедиться, вспомнив о вращающем действии пары сил, геометрическая сумма которых тоже равна нулю.

Вторым условием равновесия твердого тела является равенство нулю суммы моментов всех внешних сил, действующих на тело, относительно любой оси.

Таким образом, условия равновесия твердого тела в случае произвольного числа внешних сил выглядят так:

.

Источник

Условия равновесия тел

Равновесие тела

Тело находится в состоянии покоя (или движется равномерно и прямолинейно), если векторная сумма всех сил, действующих на него, равна нулю. Говорят, что силы уравновешивают друг друга. Когда мы имеем дело с телом определенной геометрической формы, при вычислении равнодействующей силы можно все силы прикладывать к центру масс тела.

Условие равновесия тел

Чтобы тело, которое не вращается, находилось в равновесии, необходимо, чтобы равнодействующая всех сил, действующий на него, была равна нулю.

Равновесие вращающегося тела. Правило моментов

Условия равенства нулю равнодействующей всех сил недостаточно, если тело может вращаться вокруг некоторой оси.

Определение. Правило моментов

Если алгебраическая сумма всех моментов, приложенных к телу относительно неподвижной оси вращения, равна нулю, то тело находится в состоянии равновесия.

В общем случае для равновесия тел необходимо выполнение двух условий: равенство нулю равнодействующей силы и соблюдение правила моментов.

Безразличное, устойчивое и неустойчивое равновесие

В механике есть разные виды равновесия. Так, различают устойчивое и неустойчивое, а также безразличное равновесие.

Линия, проведенная из центра масс башни пересекает основание приблизительно в 2,3 м от его центра.

Источник

Статика. условия равновесия. Виды равновесия.

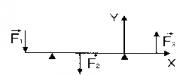
Равновесие тел при отсутствии вращения (линии действия сил пересекаются в одной точке): Векторная сумма всех сил, действующих на тело, равна нулю(алгебраическая сумма проекций всех сил на любую ось равна нулю). 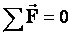или

Разновидности рычага: блок, ворот.

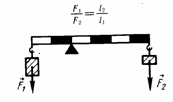
Условие равновесия рычага: отношение сил обратно пропорционально отношению плеч этих сил.

«Золотое правило механики»: выигрывая в силепроигрываешь в расстоянии.

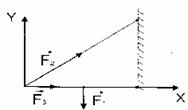
Равновесие тел при отсутствии вращения (линии действия сил не пересекаются в одной точке):

1. Векторная сумма всех сил, действующих на тело, равна нулю;

2. Алгебраическая сумма моментов всех сил, действующих на тело, относительно любой точки равна нулю.

Т.е.

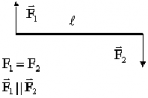
ПАРА СИЛ: Момент пары:

Пару нельзя уравновесить одной силой (равной величины)!

Примеры: завинчивание гайки гаечным ключом, вращение рамки с током в магнитном поле и т.д.

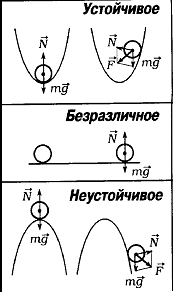
Виды равновесия:

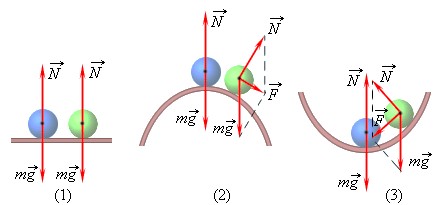
Устойчивое: При малом отклонении тела от положения равновесия возникает сила, стремящаяся возвратить тело в исходное состояние.

Безразличное: При малом отклонении тело остается в равновесии.

Неустойчивое: При малом отклонении тела из положения равновесия возникают силы, стремящиеся увеличить это отклонение.

В положении устойчивого равновесия тело обладает минимальной потенциальной энергией. При выведении тела из этого положения его потенциальная энергия увеличивается. Если работу над телом совершает только сила тяжести, то в положении устойчивого равновесия центр тяжести тела находится на наименьшей высоте.

Все тела стремятся к минимуму потенциальной энергии. (Потенциальная яма).

Равновесие тел на опоре: линия действия силы тяжести проходит через площадь опоры (Пизанская башня). Чем ниже центр тяжести, тем более устойчиво равновесие.

Источник

Статика

Статика – это раздел механики, изучающий условия равновесия тел.

Виды равновесия тел

Момент силы

Момент силы – это физическая величина, равная произведению модуля силы на ее плечо.

Обозначение – ​ \( M \) ​, единицы измерения – Н·м.

где ​ \( d \) ​ – плечо силы ​ \( F \) ​.

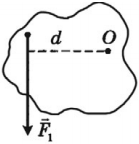
Плечо силы – это кратчайшее расстояние (перпендикуляр) от оси вращения до прямой, вдоль которой действует сила.
Обозначение – ​ \( d \) ​ или ​ \( l \) ​, единицы измерения – м.

Знак момента силы

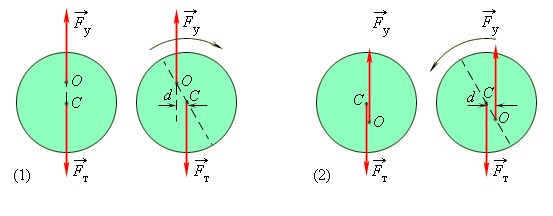
Если сила, приложенная к телу, вращает его по часовой стрелке, то момент силы положителен (​ \( M \) ​ > 0):

Если сила, приложенная к телу, вращает его против часовой стрелки, то момент силы отрицателен ( \( M \) Условия равновесия тел

Тело находится в равновесии, если

Центр тяжести – это точка внутри тела или вне его, относительно которой сумма моментов сил тяжести, действующих на отдельные его части, равна нулю.
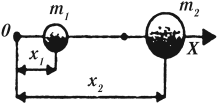
Центр масс – геометрическая точка, положение которой характеризует распределение масс в теле:

Важно!
Для твердого тела центр тяжести совпадает с центром масс.

Простые механизмы

Простые механизмы – это приспособления, служащие для преобразования силы.

Рычаг – это простейшее механическое устройство, представляющее собой твердое тело (перекладину), вращающееся вокруг точки опоры.

Рычаг дает выигрыш в силе:

Блок — простое механическое устройство, представляющее собой колесо с желобом по окружности, вращающееся вокруг своей оси. Желоб предназначен для каната, цепи, ремня и т. п.
Блок бывает подвижный и неподвижный.

Неподвижный блок – это блок, ось которого закреплена.

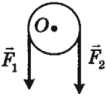
Неподвижный блок не дает выигрыша в силе, он используется для изменения направления действия силы.

Подвижный блок – это блок, имеющий свободную ось.

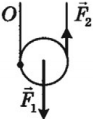
Подвижный блок дает выигрыш в силе в 2 раза:

«Золотое правило» механики

При использовании простых механизмов во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, т. е. простые механизмы выигрыша в работе не дают.

Давление жидкости

Давление жидкости – это величина, равная произведению плотности жидкости на модуль ускорения свободного падения и на высоту столба жидкости.

где ​ \( \rho \) ​ – плотность жидкости,
​ \( h \) ​ – высота столба жидкости.

Сила давления жидкости – это сила, равная произведению давления жидкости на площадь поверхности:

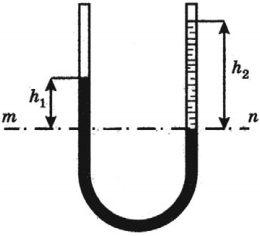
Сообщающиеся сосуды

Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости.

Закон сообщающихся сосудов:
в неподвижных и открытых сообщающихся сосудах любой формы давление жидкости на любом горизонтальном уровне одинаково.

Следствия из закона сообщающихся сосудов:

Важно!
Давление, которое создает жидкость, находящаяся в равновесии при действии на нее силы тяжести, называют гидростатическим. Гидростатическое давление определяется формулой ​ \( p=\rho gh \) ​.
Давление внутри жидкости на любой глубине складывается из атмосферного давления, или внешнего давления на жидкость, и гидростатического давления:

где ​ \( p_0 \) ​ – атмосферное давление.

Закон Паскаля

Закон Паскаля
Давление, производимое на жидкость или газ, передается по всем направлениям одинаково.

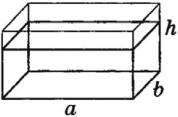
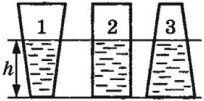
Следствие из закона Паскаля — гидростатический парадокс: давление, производимое на дно сосуда, зависит только от высоты столба жидкости:

Сила давления жидкости на дно разная, т.к. она зависит от площади дна:

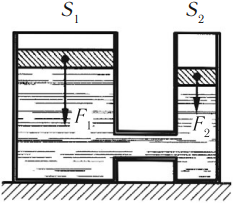
Гидравлический пресс – два сообщающихся сосуда, заполненные жидкостью и закрытые поршнями различной площади.
Гидравлический пресс дает выигрыш в силе, но проигрыш в длине пути поршня:

Силы, действующие на поршни гидравлического пресса, пропорциональны площадям этих поршней:

Атмосферное давление – это давление, которое оказывает атмосфера на все находящиеся в ней предметы.
Атмосферное давление уменьшается с увеличением высоты подъема над Землей.

Нормальное атмосферное давление: ​ \( p_0 \) ​ = 10 5 Па.

Приборы для измерения давления:

Закон Архимеда

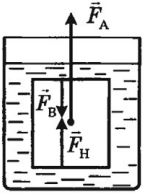
Архимедова сила – это выталкивающая сила, действующая на тело, погруженное в жидкость или газ.

Причина возникновения выталкивающей силы – разница давлений жидкости или газа на верхнюю и нижнюю грани.
Архимедова сила всегда направлена перпендикулярно поверхности жидкости.
Архимедова сила равна разности веса тела в воздухе и веса тела в жидкости или газе:

где ​ \( P_1 \) ​ – вес тела в воздухе,
​ \( P_2 \) ​ – вес тела в жидкости или газе.

Закон Архимеда
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу жидкости или газа, вытесненных телом:

Если тело полностью погружено в жидкость, то

где ​ \( V_m \) ​ – объем тела, погруженного в жидкость.

Если тело не полностью погружено в жидкость, то

где ​ \( V_ <чm>\) ​ – объем части тела, погруженной в жидкость.

Условия плавания тел

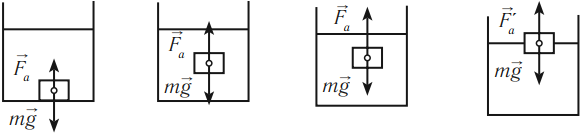
На любое тело, погруженное в жидкость или газ, действуют две силы, направленные в противоположные стороны, – это сила тяжести и архимедова сила. Направление движения тела зависит от того, какая из этих сил больше по модулю.

Условия плавания тел

где ​ \( V_1 \) ​ – объем части тела, погруженной в жидкость.

Важно!
Выталкивающая сила действует на тела в жидкостях и газах, потому что сжаты силой притяжения к Земле. В состоянии невесомости эта сила не действует.

Источник

Условия равновесия тел

Статикой называется раздел механики, изучающий условия равновесия тел.

Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс.

Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.

или

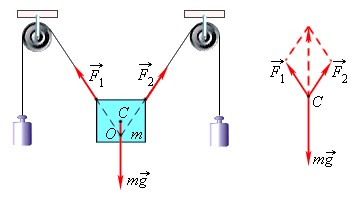
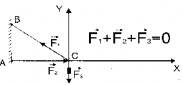
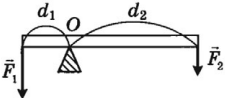
Равновесие твердого тела под действием трех сил. При вычислении равнодействующей все силы приводятся к одной точке C

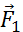
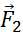
На рис. 1.14.1 дан пример равновесия твердого тела под действием трех сил. Точка пересечения O линий действия сил и не совпадает с точкой приложения силы тяжести (центр масс C), но при равновесии эти точки обязательно находятся на одной вертикали. При вычислении равнодействующей все силы приводятся к одной точке.

Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил.

Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения.

Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.

Произведение модуля силы 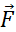на плечо d называется моментом силы M. Положительными считаются моменты тех сил, которые стремятся повернуть тело против часовой стрелки (рис. 1.14.2).

Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:

В Международной системе единиц (СИ) моменты сил измеряются в Ньютон—метрах (Н∙м).

Источник